




2.2 数据预处理方法介绍 |

|
当我们拿到一批原始的数据,步骤如下:
(1)首先要明确有多少特征,哪些是连续的特征,哪些是类别的特征?
(2)检查有没有缺失值,对确实的特征选择恰当方式进行弥补,使数据完整。
(3)对连续的数值型特征进行标准化,使得均值为0,方差为1。
(4)对类别型的特征进行独热编码(One-Hot Encoding)。
(5)将需要转换成类别型数据的连续型数据进行二值化。
(6)为防止过拟合或者其他原因,选择是否要将数据进行正则化。
数据预处理的工具有许多,主要有两种:Pandas数据预处理和scikit-learn中的sklearn.preprocessing数据预处理。本章主要使用sklearn.preprocessing包进行数据预处理。
在机器学习算法实践中,我们往往有着这些需求:将不同规格的数据转换到同一规格中用,或将不同分布的数据转换到某个特定分布中,这种需求统称为将数据“无量纲化”。标准化则是将数据按照比例缩放,使之放到一个特定区间中。标准化后数据的均值=0,标准差=1,因而标准化的数据可正可负,只不过归一化是将数据映射到了[0,1]这个区间中。
把数据缩放到给定的范围内,通常在0和1之间,或者使用每个特征的最大绝对值按比例缩放到单位大小。在大多数机器学习算法中,会选择StandardScaler来进行特征缩放,因为MinMaxScaler对异常值非常敏感。在PCA、聚类、逻辑回归、支持向量机、神经网络这些算法中,StandardScaler往往是最好的选择。MinMaxScaler在不涉及距离度量、梯度、协方差计算以及数据需要被压缩到特定区间的情况下使用广泛,比如数字图像处理中量化像素强度时,都会使用MinMaxScaler将数据压缩于[0,1]区间之中。
程序代码如下:

运行上面这段代码,结果如图2-1所示。
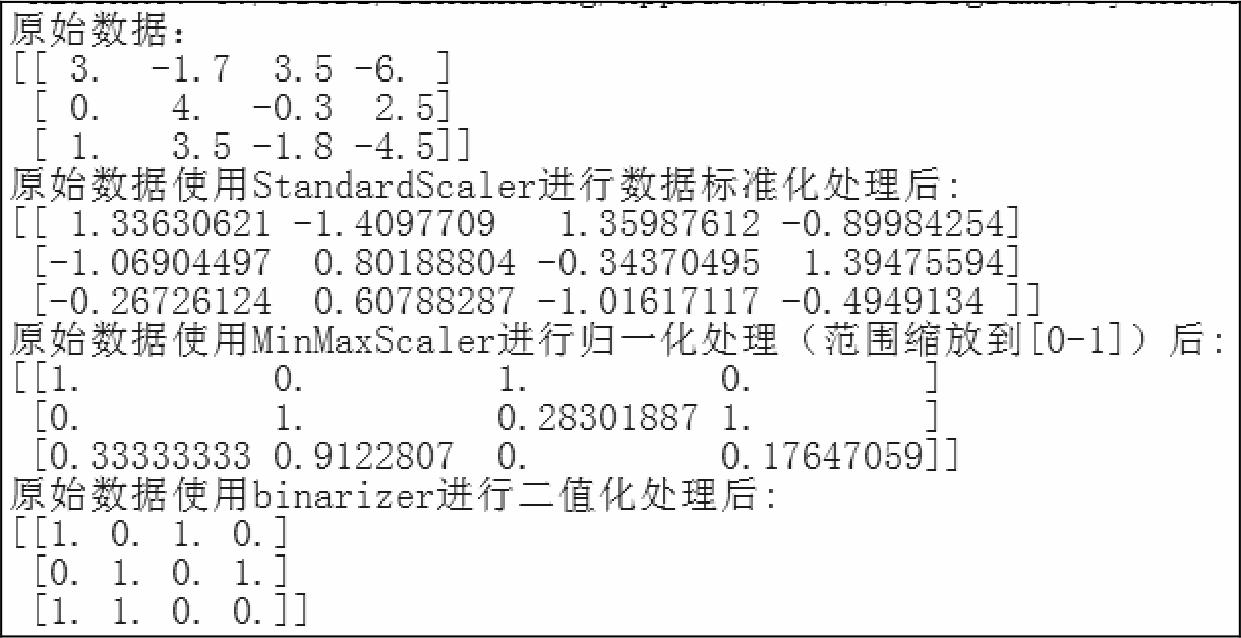
图2-1
StandardScaler标准化的原理是将特征数据的分布调整成标准正态分布,也叫高斯分布,也就是使得数据的均值为0,方差为1,这样就可以确保数据的“大小”都是一致的,这样更有利于模型的训练。而MinMaxScaler把所有的数据缩放到0和1之间。除了对数据进行缩放之外,我们还可以使用Binarizer对数据进行二值化处理,将不同的数据全部处理为0或1这两个数值。归一化其实就是标准化的一种方式,只不过归一化是将数据映射到[0,1]这个区间中。
很多情况下,真实的数据集中会存在缺失值,此时需要对缺失值进行处理。一种策略是将存在缺失值的整条记录直接删除。但是这样做可能会丢失一部分有价值的信息。更好的一种方法是推定缺失数据,例如根据已有数据推算缺失的数据。SKImputer类能够提供一些处理缺失值的基本策略,例如使用缺失值所处的一行或者一列的均值、中位数或者出现频率最高的值作为缺失数据的取值。我们得到的数据可能由于各种原因存在缺失。为了不降低机器学习模型的性能,我们可以通过一些方法处理这些数据,比如使用整列数据的平均值或中位数来替换丢失的数据。
Label Encoder就是把label编码。比如label是一串地名,是无法直接输入到sklearn的分类模型里作为训练标签的,所以需要先把地名转成数字。这里Label Encoder就是帮你做这件事的。
范例程序代码如下:

运行这个范例程序,结果如图2-2所示。

图2-2
使用sklearn.preprocessing库中的Imputer类来完成这项任务。
Imputer参数解释:
(1)missing_values:缺失值,可以为整数或NaN,默认为NaN。
(2)strategy:替换策略,默认用均值“mean”替换,还可以选择中位数“median”或众数“most_frequent”。
(3)axis:指定轴数,默认axis=0代表列,axis=1代表行。
在机器学习算法中,我们经常会遇到分类特征,例如:人的性别有男、女,祖国有中国、美国、法国等。这些特征值并不是连续的,而是离散的、无序的。通常我们需要对其进行特征数字化。其中一种可能的解决方法是采用独热编码(One-Hot Encoding)。独热编码又称为一位有效编码,其方法是使用N位状态寄存器来对N个状态进行编码,每个状态都有它独立的寄存器位,并且在任意时候,其中只有一位有效。可以这样理解,对于每一个特征,如果它有m个可能值,那么经过独热编码后,就变成了m个二元特征(如成绩这个特征有好、中、差,变成独热编码就是100, 010, 001)。并且,这些特征互斥,每次只有一个激活。因此,数据会变成稀疏的数据。
举个例子如下:
性别特征:["男","女"]
国家特征:["中国","美国,"法国"]
体育运动特征:["足球","篮球","羽毛球","乒乓球"]
假如某个样本(某个人),他的特征是这样的:["女","中国","羽毛球"],我们如何将特征数字化呢?即转化为数字表示后,上述数据要能直接用在我们的分类器中,分类器往往默认数据是连续的,并且是有序的。
用独热编码来解决上述问题,做法如下:
性别特征:["男","女"],按照N位状态寄存器来对N个状态进行编码,处理后应该是这样的(这里只有两个特征,所以N=2):
男 ⇒ 10
女 ⇒ 01
国家特征:["中国","美国,"法国"](这里N=3):
中国 ⇒ 100
美国 ⇒ 010
法国 ⇒ 001
运动特征:["足球","篮球","羽毛球","乒乓球"](这里N=4):
足球 ⇒ 1000
篮球 ⇒ 0100
羽毛球 ⇒ 0010
乒乓球 ⇒ 0001
所以,当一个样本为["女","中国","羽毛球"]的时候,完整的特征数字化的结果为:
[0,1,1,0,0,0,0,1,0]
范例程序代码如下:

这个范例程序的运行结果如图2-3所示。数据矩阵是4×3,即4个数据,3个特征维度。观察左边的数据矩阵,第一列为第一个特征维度,有两种取值0\1,所以对应的编码方式为10、01。同理,第二列为第二个特征维度,有三种取值0\1\2,所以对应的编码方式为100、010、001。同理,第三列为第三个特征维度,有四种取值0\1\2\3,所以对应的编码方式为1000、0100、0010、0001。再来看要进行编码的参数[0, 1, 3],0作为第一个特征编码为10,1作为第二个特征编码为010,3作为第三个特征编码为0001,故此编码结果为[ 1 0 0 1 0 0 0 0 1]。

图2-3
独热编码解决了分类器不好处理属性数据的问题,在一定程度上也起到了扩充特征的作用。它的值只有0和1,不同的类型存储在垂直的空间中。缺点是当类别的数量很多时,特征空间会变得非常大。
独热编码用来解决类别型数据的离散值问题,将离散型特征进行独热编码的作用,是为了让距离计算更合理,但如果特征是离散的,并且不用独热编码就可以很合理地计算出距离,这样就没必要进行独热编码。有些基于树的算法在处理变量时,并不是基于向量空间度量,数值只是个类别符号,即没有偏序关系,所以不用进行独热编码。
数据预处理的意义究竟有多大?我们使用酒的数据集来测试一下,这里使用多层神经网络模型,神经网络的概念后续章节中会详细介绍,这里只是给读者一个数据预处理对模型的准确率的影响究竟有多大的理性认识。
范例程序代码如下:

运行这个范例程序,结果如图2-4所示,训练集样本数目为133,而测试集中样本数量为45个。我们用训练数据集来训练一个MLP多层神经网络(后面章节会详细介绍神经网络),在没有经过数据预处理的情况下,模型的得分只有0.24。当对数据集进行预处理后,模型的评分大幅提高,直接提升到了1.00。

图2-4