




图(Graph)是由顶点的有穷非空集合和顶点之间边的集合组成的,通常表示为:G(V,E),其中,G表示一个图,V是图G中顶点的集合,E是图G中边的集合。
(1)顶点。顶点是图的基本单元之一,相当于树中的结点。
(2)边。图中顶点之间的关联关系。
(3)无向边。若两个顶点之间的边没有方向,则称这条边为无向边。
(4)无向图。任意两个顶点之间的边都是无向边的图称为无向图。
(5)有向边。若两个顶点之间的边是有方向的,则称为有向边。
(6)有向图。任意两个顶点之间的边都是有向边的图称为有向图。
(7)简单图。不存在自环(指向顶点自身的边)和重边(完全相同的多条边)的图。
(8)无向完全图。任意两个顶点间都存在边的无向图称为无向完全图。
(9)有向完全图。任意两个顶点间都存在方向相反的两条边的有向图称为有向完全图。
(10)稀疏图。只有很少条边组成的图称为稀疏图。
(11)稠密图。有很多条边组成的图称为稠密图。
(12)权重。从图中一个顶点到另一个顶点的距离或耗费。
(13)带权图。带有权重的图称为带权图。
(14)度。与顶点相连接的边的数目称为度。
(15)出度。有向图中的概念,出度表示以此顶点为起点的边的数目。
(16)入度。有向图中的概念,入度表示以此顶点为终点的边的数目。
(17)环。开始顶点和结束顶点相同的路径称为环。
(18)简单环。除去第一个顶点和最后一个顶点后没有重复顶点的环。
(19)连通图。任意两个顶点都互相连通的图。
(20)非连通图。存在不能互相连通的顶点的图称为非连通图。
(21)极大连通子图。加入任何一个不在图的点都会导致图不再连通,此时的图就是极大连通子图。连通图的极大连通子图是自身,非连通图存在多个极大连通子图。
(22)连通分量。无向图的极大连通子图称为连通分量。任何连通图的连通分量只有一个,就是其自身,非连通的无向图有多个连通分量。
(23)生成树。对连通图进行遍历,过程中所经过的边和顶点的组合可看作一棵普通树,通常称为生成树。
(24)最小生成树:对连通图来说,边的权重之和最小的生成树称为最小生成树。
(25)AOV网。用顶点表示活动,用边表示活动间的优先关系的有向图称为AOV网。
(26)AOE网。带权有向图中以顶点表示事件,有向边表示活动,边上的权值表示该活动持续的时间,这样的图称为AOE网。
图的结构比较复杂,任意两个顶点之间都可能存在关系,因此用简单的顺序存储来表示图是很难实现的,而若使用多重链表的方式(一个数据域、多个指针域的结点来表示),则会出现严重的空间浪费或操作不便。图的常用存储结构有邻接矩阵、邻接表和十字链表。下面将一一分析这3种存储结构。
邻接矩阵(Adjacency Matrix)使用两个数组存储图,其中一个一维数组用于存储图中的顶点,另一个二维数组存储顶点之间的边的信息。以图2-123所示的无向图为例,使用邻接矩阵进行存储。
使用邻接矩阵存储图2-123所示的无向图,其中顶点间有边相连的用数值1表示,顶点间没有边相连的用数值∞表示。图2-123所示的无向图的邻接矩阵存储如图2-124所示。
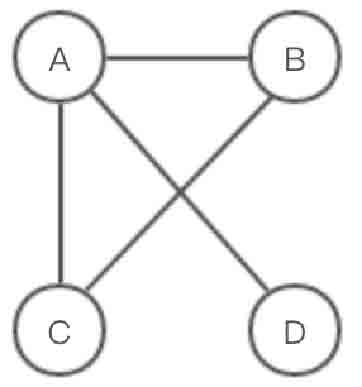
图2-123 无向图示意图
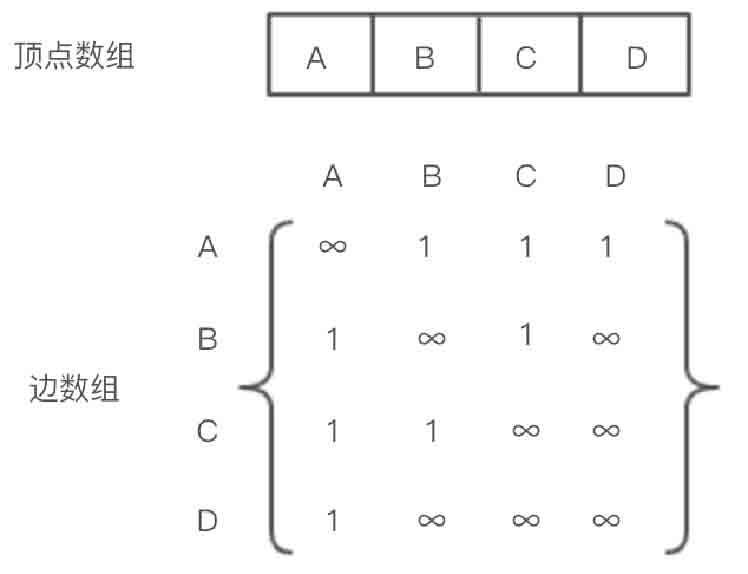
图2-124 无向图邻接矩阵存储示意图
因为无向图的边不区分方向,所以无向图的邻接矩阵的实现是一个对称矩阵。
以图2-125所示的有向图为例,使用邻接矩阵进行存储。
图2-125所示的有向图的邻接矩阵存储如图2-126所示。
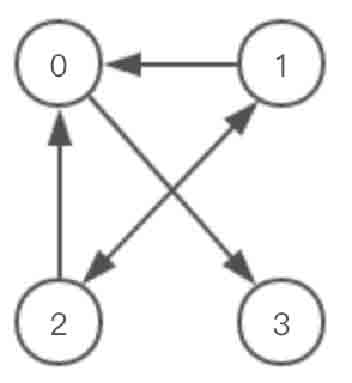
图2-125 有向图示意图
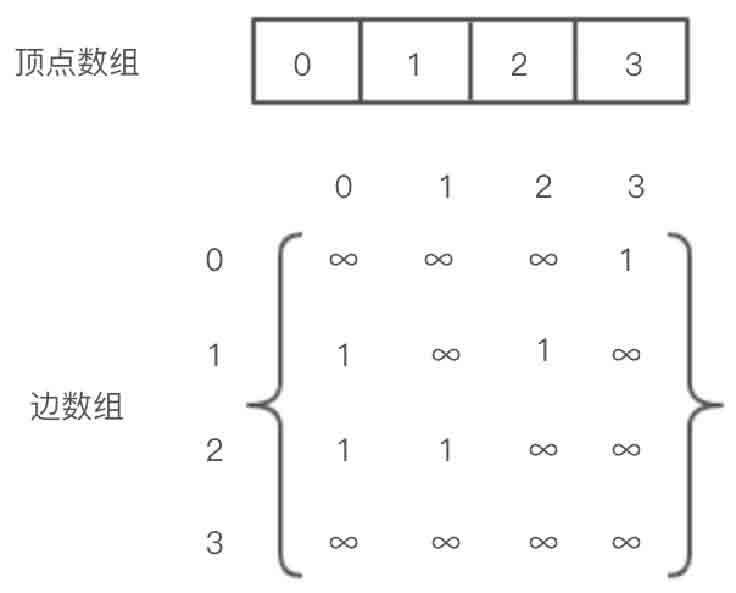
图2-126 有向图邻接矩阵存储示意图
下面以有向图为例,阐述邻接矩阵的实现。


创建邻接矩阵的测试类,用于验证邻接矩阵的功能:
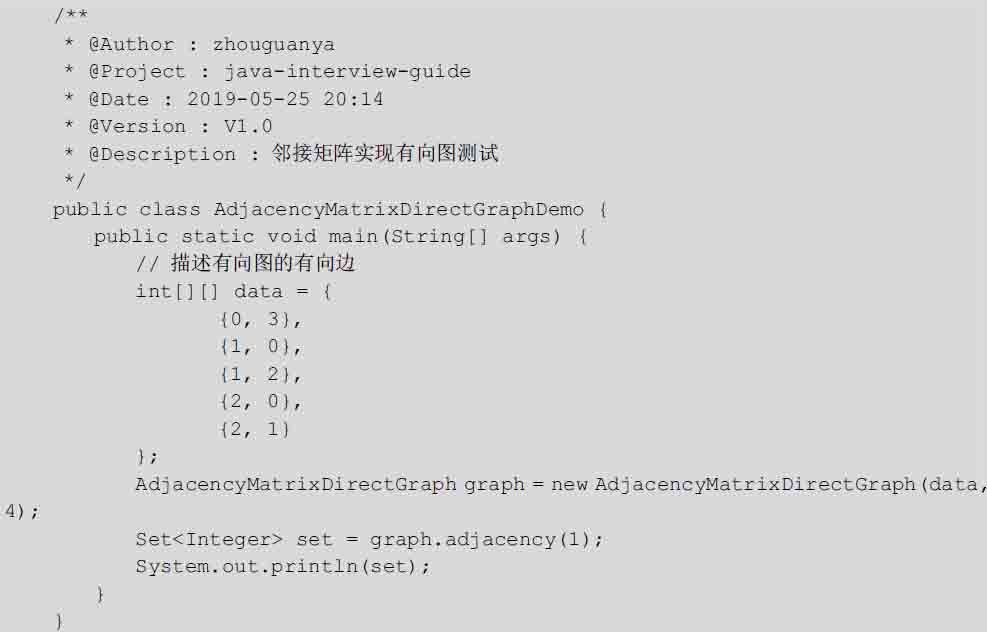
执行测试代码,执行结果如下:
顶点1的邻接点为:[0, 2]
邻接矩阵的优点:邻接矩阵的结构简单,操作方便。
邻接矩阵的缺点:邻接矩阵存储稀疏图,将会造成大量的空间浪费。
邻接表是一种将数组与链表相结合的存储方法。其具体实现为:将图中顶点用一个一维数组存储,每个顶点所有邻接点用一个单链表来存储。以图2-127所示的无向图为例,使用邻接表进行存储。
图2-127所示的无向图用邻接表存储示意图如图2-128所示。
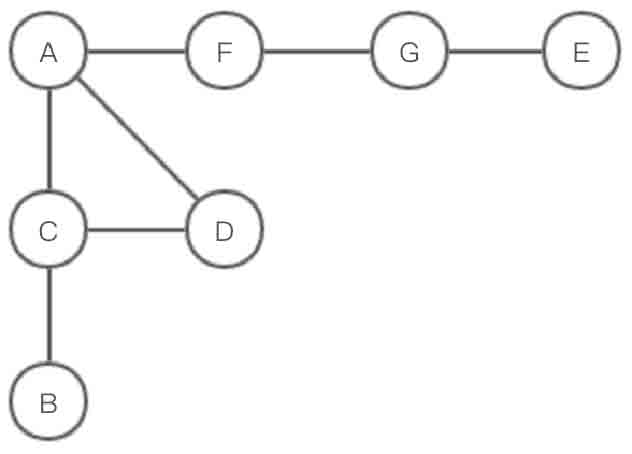
图2-127 无向图示意图
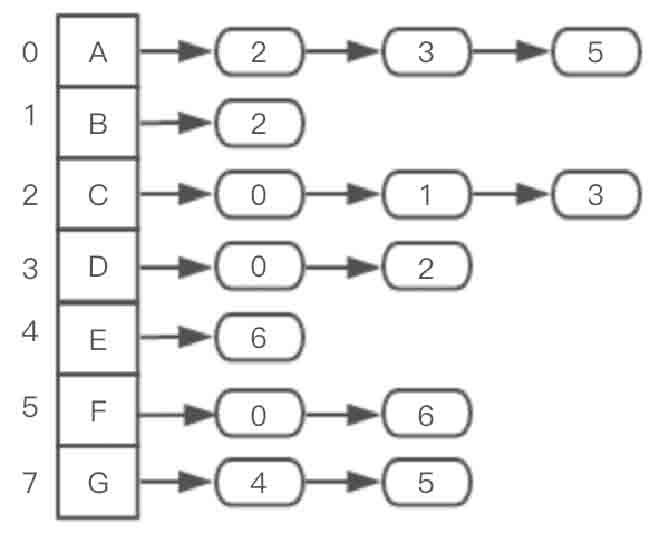
图2-128 无向图用邻接表存储示意图
在图2-128所示的邻接表示意图中,一维数组中存储了无向图的顶点信息,每个顶点拥有一个指向一条单链表的引用,单链表中的每个结点记录了对应的顶点连接点的位置。例如,第2个顶点(顶点C)指向的链表所包含的结点的数据分别是“0,1,3”,而“0,1,3”分别对应“A,B,D”的序号,因此C的邻接点是“A,B,D”。
下面以无向图为例阐述邻接表的实现。




创建邻接表的测试类,用于验证邻接表的功能:

执行测试代码,执行结果如下:
顶点A的邻接点有:C
顶点A的邻接点有:D
顶点A的邻接点有:F
顶点B的邻接点有:C
顶点C的邻接点有:A
顶点C的邻接点有:B
顶点C的邻接点有:D
顶点D的邻接点有:A
顶点D的邻接点有:C
顶点E的邻接点有:G
顶点F的邻接点有:A
顶点F的邻接点有:G
顶点G的邻接点有:E
顶点G的邻接点有:F
邻接矩阵的实现虽然非常简单,但是其缺点也暴露得非常明显。当存储的是稀疏图时(图的顶点较多,边较少),寻找一个点能连到的所有点的代价非常大,需要把矩阵每一行都遍历一次。此外,存储邻接矩阵需要顶点数量的平方个存储空间,对于稀疏图而言,矩阵中会存在大量∞表示两个点之间没有连线,这样会存在非常大的空间浪费。
邻接表在存储稀疏图时,相比邻接矩阵是有明显优势的,从一个特定顶点出发去寻找邻接点时不需要把所有点都遍历一遍。但是邻接表在处理一些特殊问题时遇到一些麻烦,如不能沿着边反向查找。在图2-128所示的邻接表中,如果需要寻找所有能连接到顶点A的点,就需要把C、D和F指向的链表都搜索一遍,极端情况下可能得把整个图都遍历一次。这种情况下,邻接表的查找效率非常低下。
基于以上图的邻接矩阵实现结构和图的邻接表存储结构的缺点,更加健壮的数据结构十字链表诞生了。
逆邻接表:任一表头结点下的边结点的数量是图中该结点入度的弧的数量,与邻接表相反。图的邻接表反映的是结点的出度邻接情况,图的逆邻接表反映的是结点的入度邻接情况。
十字链表(Orthogonal List)是有向图的另一种链式存储结构。该结构可以看成是将有向图的邻接表和逆邻接表结合起来得到的。
以图2-129所示的有向图为例,使用十字表进行存储。
图2-129所示的有向图十字链表存储结构如图2-130所示。
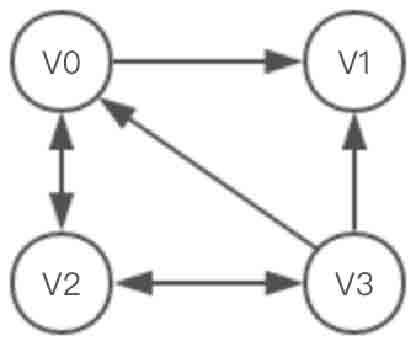
图2-129 有向图示意图
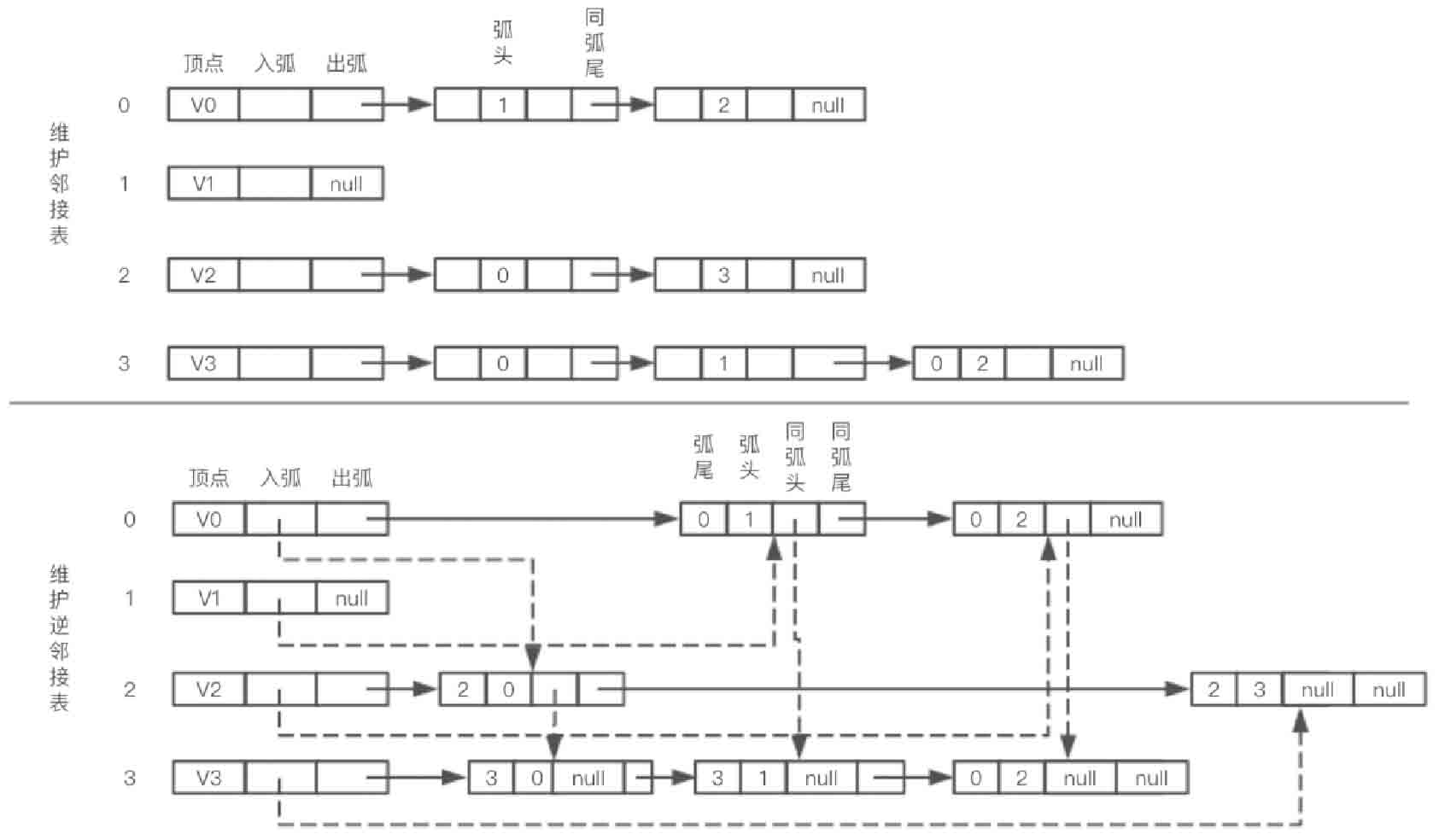
图2-130 有向图十字链表存储示意图
下面以有向图为例,阐述十字链表的实现。





创建十字链表的测试类,用于验证十字链表的功能:
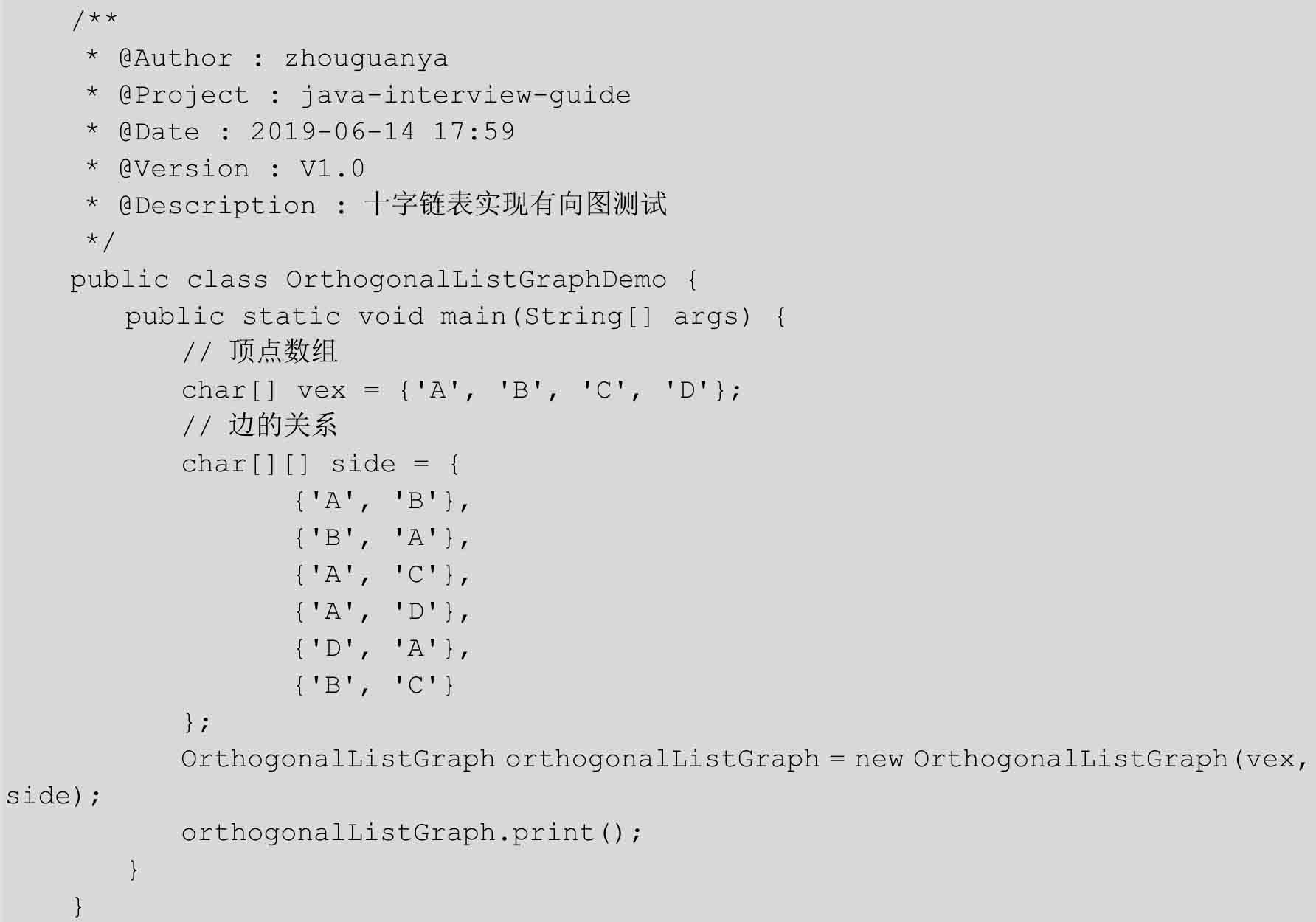
执行测试代码,执行结果如下:
邻接表:
A->D,C,B
B->C,A
C->
D->A
逆邻接表
A<-D,B
B<-A
C<-B,A
D<-A
从图的某个顶点出发,遍历图中其余顶点,且使每个顶点仅被访问一次,这个过程叫作图的遍历(Traversing Graph)。对于图的遍历通常有两种方法:深度优先遍历和广度优先遍历。
图的深度优先遍历思想:从图中某个顶点出发,首先访问此顶点,然后依次从该顶点相邻的顶点出发深度优先遍历,直至图中所有与该顶点路径相通的顶点都被访问;若此时图中还有顶点未被访问,则从中选一个顶点作为起始点,重复上述过程,直到所有的顶点都被访问。
以图2-131所示的无向图为例,阐述图的深度优先遍历过程。
图2-131所示的无向图的深度优先遍历过程如图2-132所示。其中白色结点表示未访问的结点,黑色结点表示已经访问的结点。
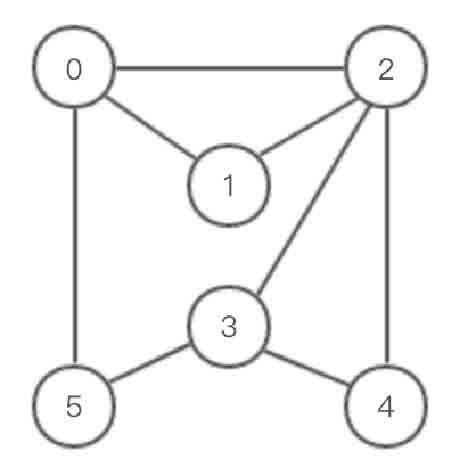
图2-131 无向图示意图
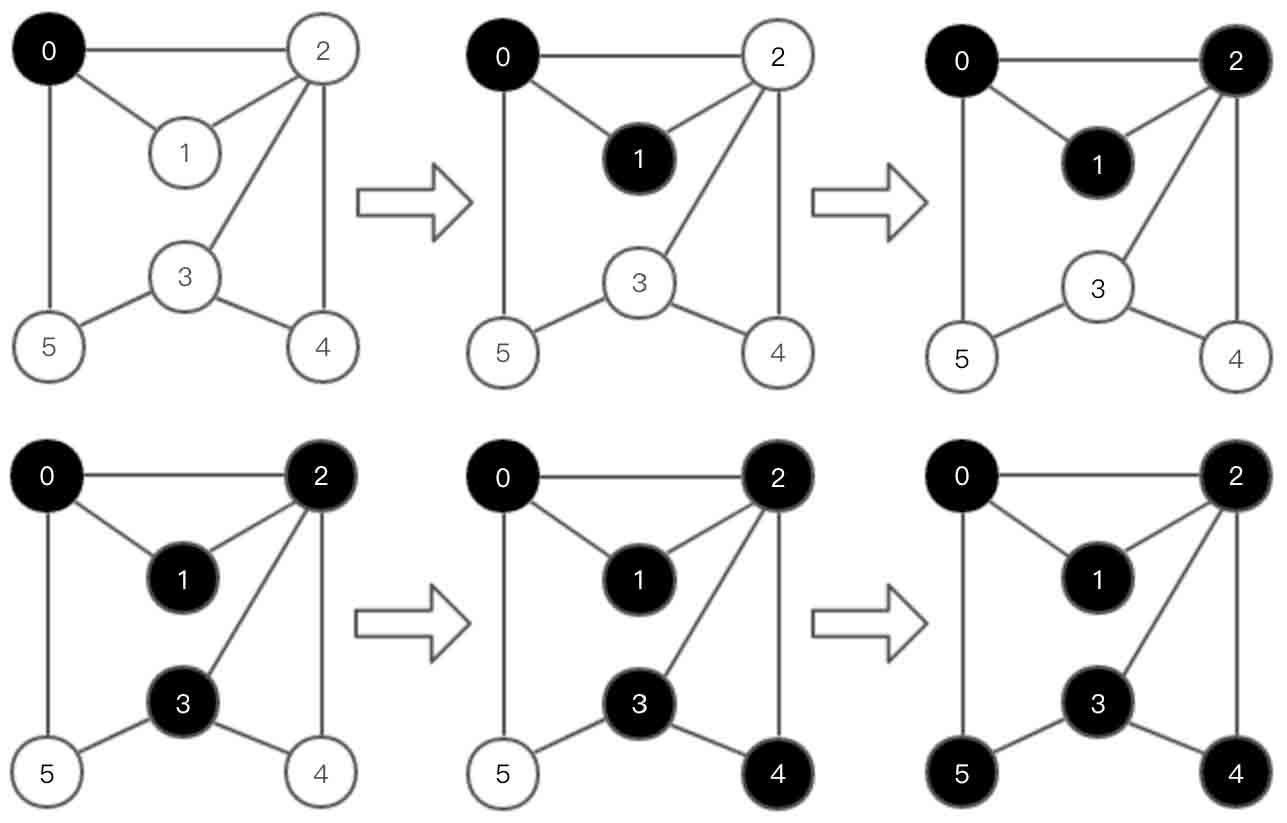
图2-132 无向图深度优先遍历示意图
图的深度优先遍历用一个递归方法来遍历所有顶点,在访问某一个顶点时:
(1)将该顶点标记为已访问。
(2)以递归地方式访问该顶点的所有未被标记过的邻接点。
图的深度优先遍历实现如下(本例中的图使用邻接表实现,邻接表的详细实现可参考2.9.3小节):

创建图的深度优先遍历的测试类,用于验证图的深度优先遍历的功能:

执行测试代码,执行结果如下:
从顶点0开始图的深度优先遍历:0 1 2 3 4 5
广度优先遍历(Breadth First Search,BFS)又称为广度优先搜索。图的广度优先遍历思想:从图的某个顶点出发,首先访问该顶点,然后依次访问与该顶点相邻的未被访问的顶点,接着分别从这些顶点出发,进行广度优先遍历,直至所有的顶点都被访问完。
以图2-133所示的无向图为例阐述图的广度优先遍历过程。其中白色结点表示未访问的结点,黑色结点表示已经访问的结点。
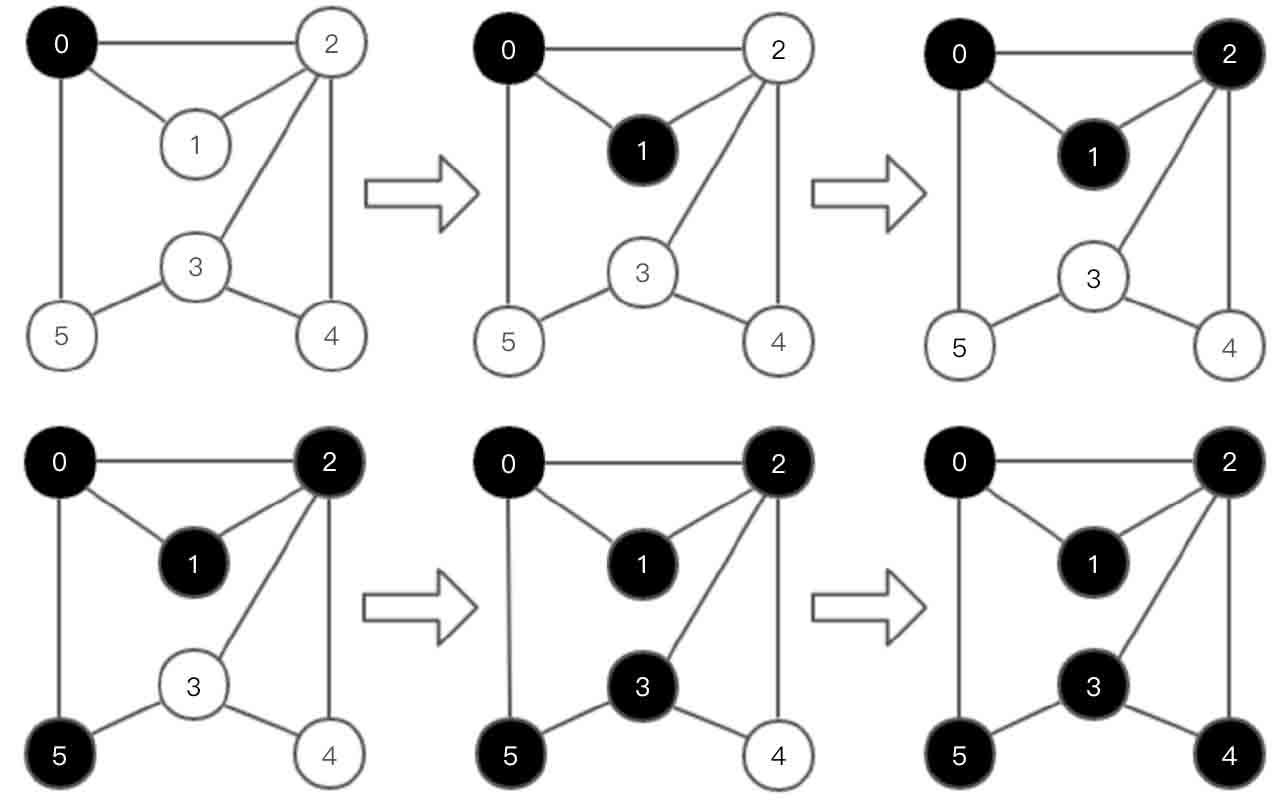
图2-133 无向图广度优先遍历示意图
图的广度优先遍历实现如下(本例中的图使用邻接表实现,邻接表的详细实现可参考2.9.3小节):


创建图的广度优先遍历的测试类,用于验证图的广度优先遍历的功能:
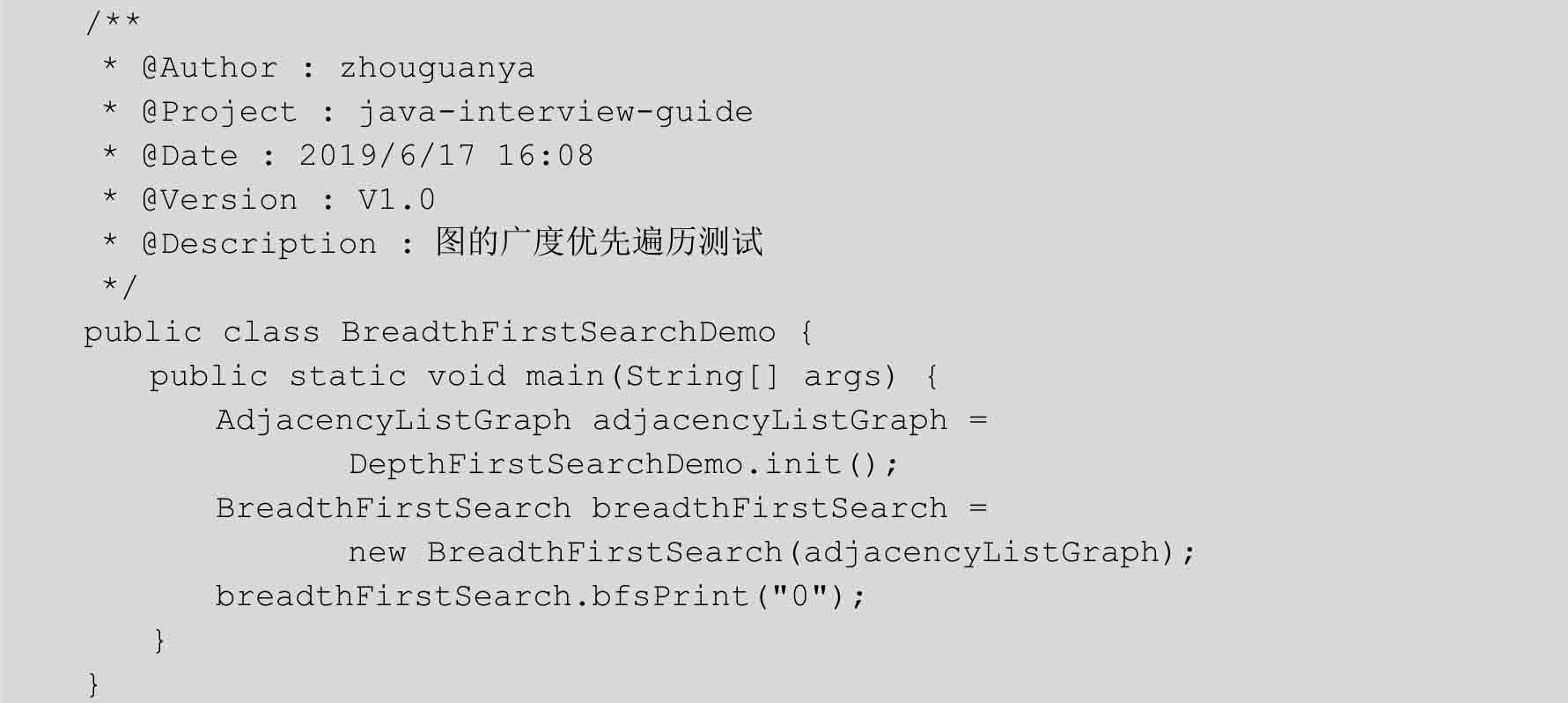
执行测试代码,执行结果如下:
从顶点0开始图的广度优先遍历:0 1 2 5 3 4
图的生成树是图的一个含有其所有顶点的无环连通子图。一幅加权图的最小生成树(Minimum Spanning Tree,MST)是其权值(所有边的权值之和)最小的生成树。加权无向图如图2-134所示。
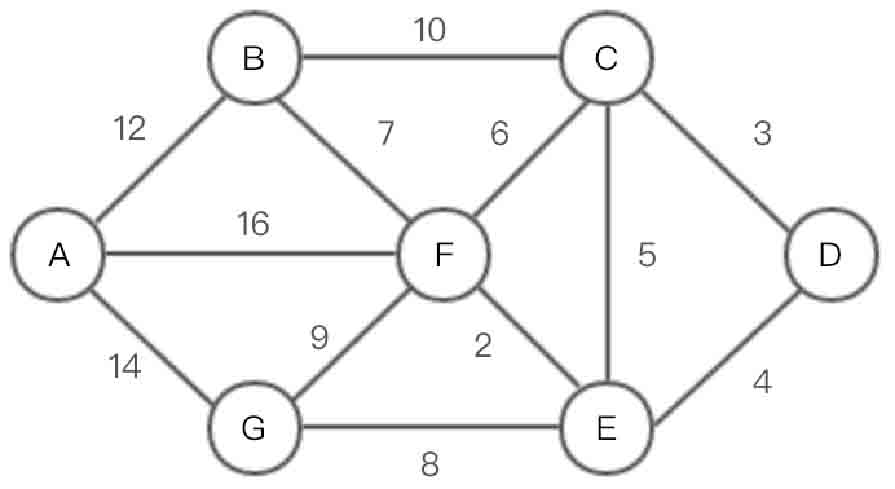
图2-134 加权无向图示意图
图2-134所示的加权无向图的最小生成树如图2-135所示。其中虚线连接的顶点和路径为最小生成树,最小生成树的权值是36。
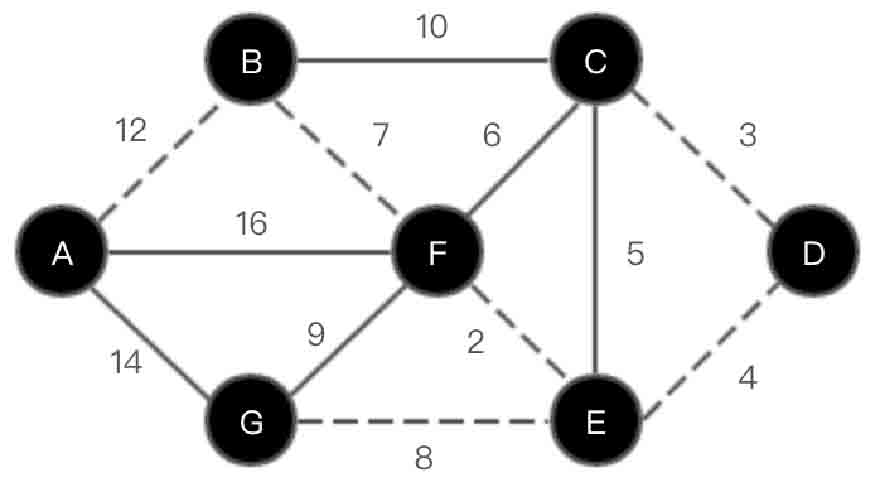
图2-135 加权无向图最小生成树示意图
普里姆(Prim)算法,是用来求加权连通图的最小生成树的算法。
Prim算法的基本思想:对于图G及其所有顶点的集合V,设置两个新的集合U和T,其中U用于存放G的最小生成树中的顶点,T存放G的最小生成树中的边。从所有U和V-U(V-U表示V中除去U的所有顶点)的边中选取权值最小的边(u, v),将顶点v加入集合U中,将边(u, v)加入集合T中,如此不断重复,直到U=V为止,最小生成树构造完毕,这时集合T中包含了最小生成树中的所有边。
以图2-134为例阐述Prim算法的执行过程。
(1)选取顶点A,在集合U中加入A。此时U={A},V-U={B,C,D,E,F,G},如图2-136所示。
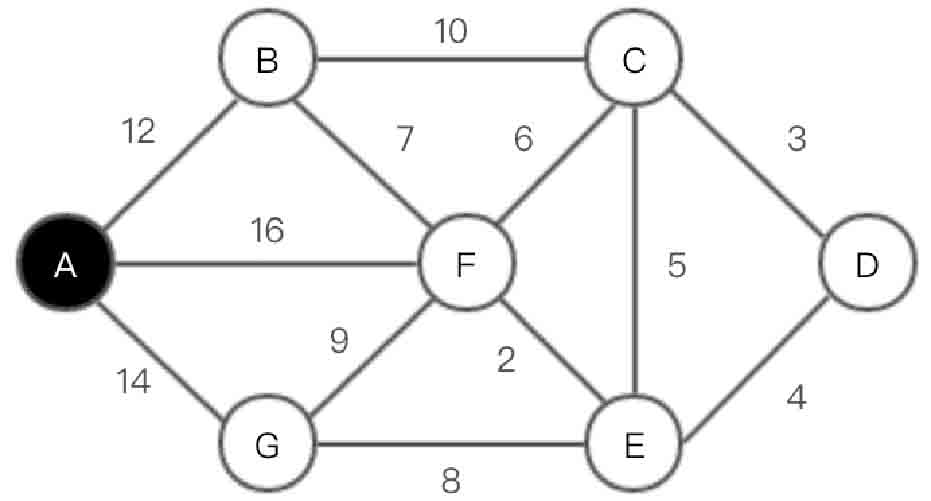
图2-136 Prim算法第(1)步示意图
(2)选取顶点B,在集合U中加入B。此时U={A,B},V-U={C,D,E,F,G},如图2-137所示。
(3)选取顶点F,在集合U中加入F。此时U={A,B,F},V-U={C,D,E,G},如图2-138所示。
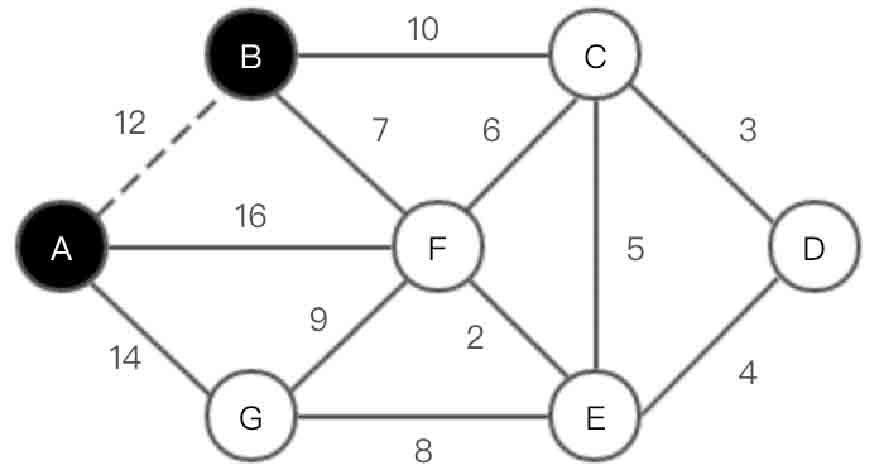
图2-137 Prim算法第(2)步示意图
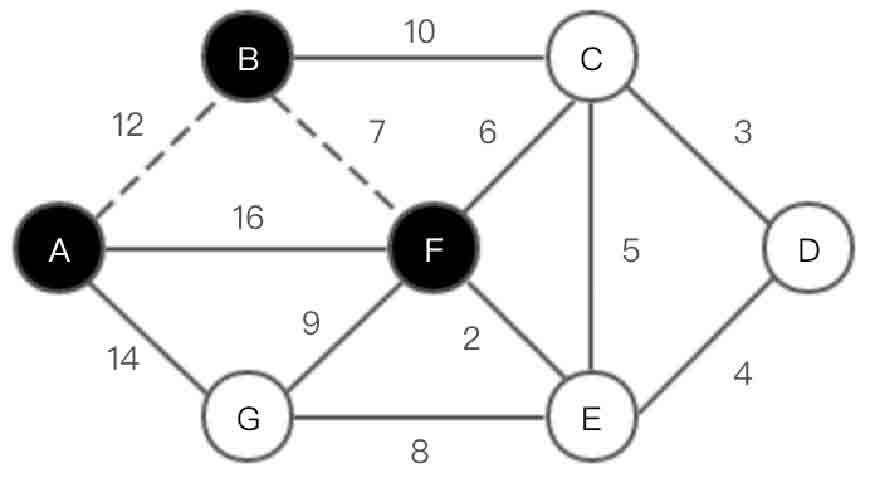
图2-138 Prim算法第(3)步示意图
(4)选取顶点E,在集合U中加入E。此时U={A,B,F,E},V-U={C,D,G},如图2-139所示。
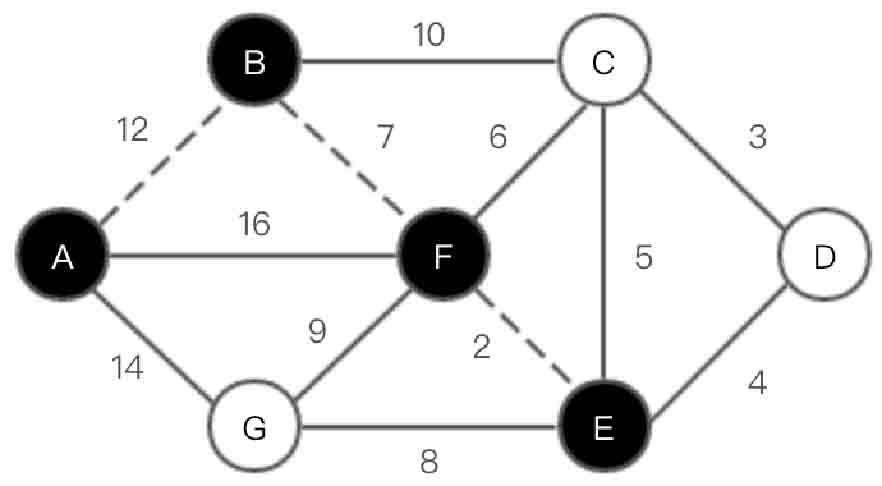
图2-139 Prim算法第(4)步示意图
(5)选取顶点D,在集合U中加入D。此时U={A,B,F,E,D},V-U={C,G},如图2-140所示。
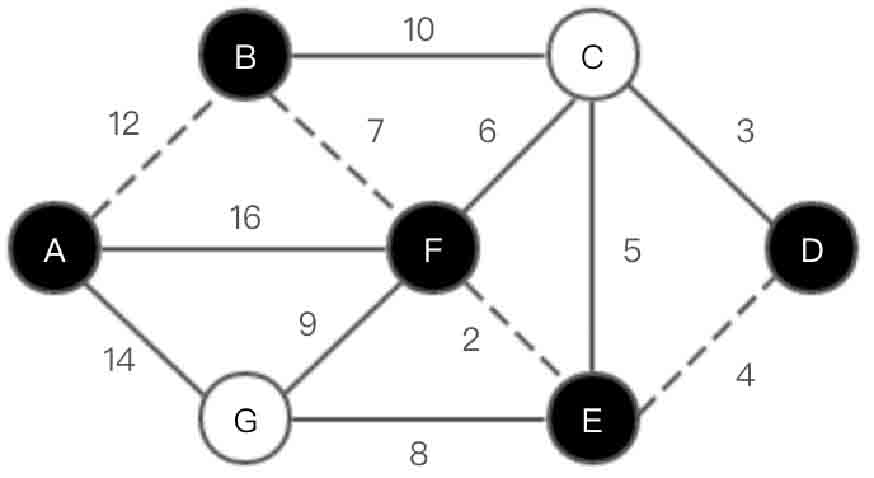
图2-140 Prim算法第(5)步示意图
(6)选取顶点C,在集合U中加入C。此时U={A,B,F,E,D,C},V-U={G},如图2-141所示。
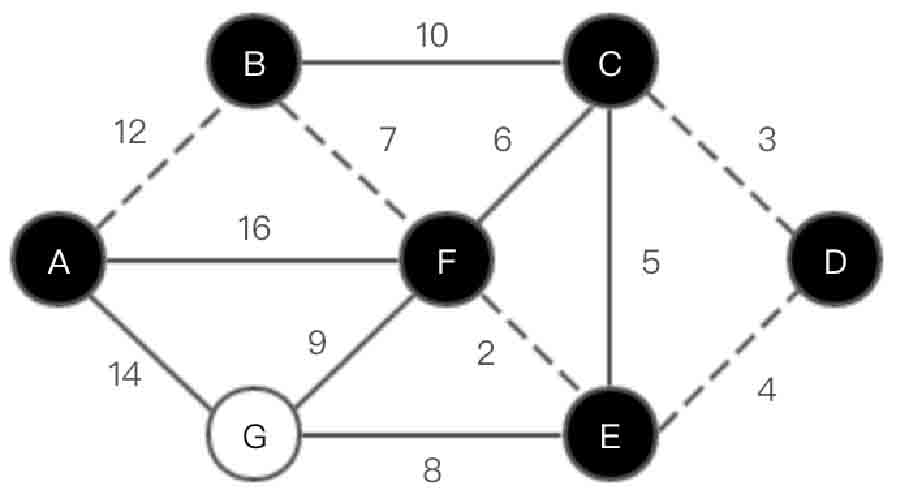
图2-141 Prim算法第(6)步示意图
(7)选取顶点G,在集合U中加入G。此时U={A,B,F,E,D,C,G},V-U={},如图2-142所示。
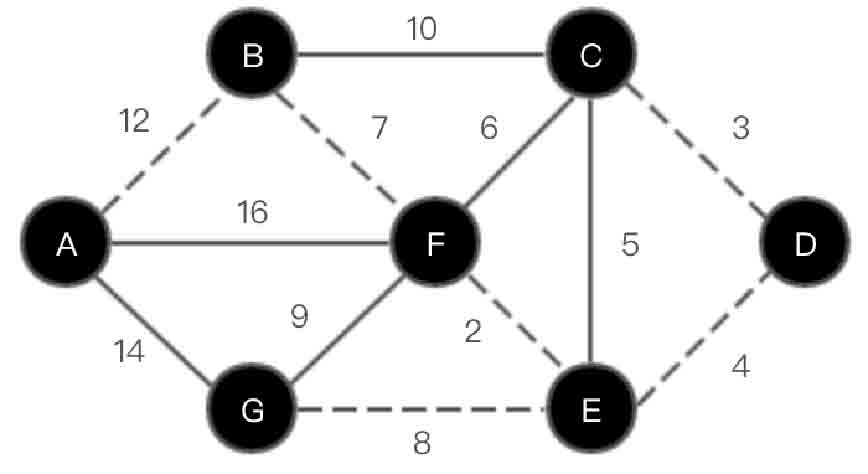
图2-142 Prim算法第(7)步示意图
经过上面7个步骤后,此时U=V,最小生成树构建完毕,其中虚线连接的顶点和路径为最小生成树,如图2-142所示。最小生成树包括的顶点依次是A、B、F、E、D、C、G。
下面通过代码实现Prim算法求解最小生成树。首先创建EdgeData用于表示带权边。

创建邻接表用于表示带权图,其实现如下:



通过Prim算法实现最小生成树。其中使用上述邻接表表示带权有向图,实现如下:



创建测试类用于验证Prim算法生成最小生成树的功能,实现如下:

执行测试代码,执行结果如下:
PRIM最小生成树=36: A B F E D C G
克鲁斯卡尔(Kruskal)算法是一种用来求加权连通图的最小生成树的算法。
Kruskal算法的核心思想:依权值从小到大从连通图中选择边加入森林中,并使森林中不产生回路,直至森林变成一棵树为止。
以图2-135为例阐述Kruskal算法的执行过程。
(1)选取边<E, F>,如图2-143所示。
(2)选取边<C, D>,如图2-144所示。
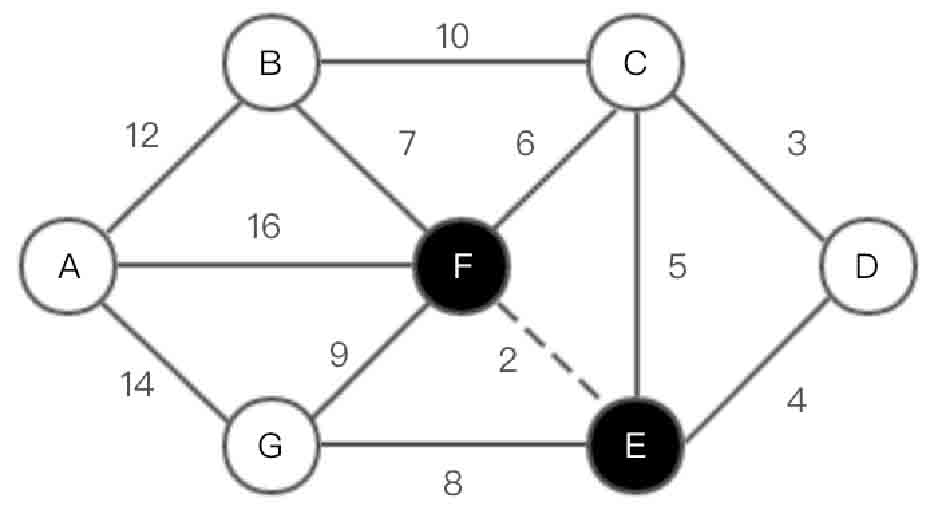
图2-143 Kruskal算法第(1)步示意图
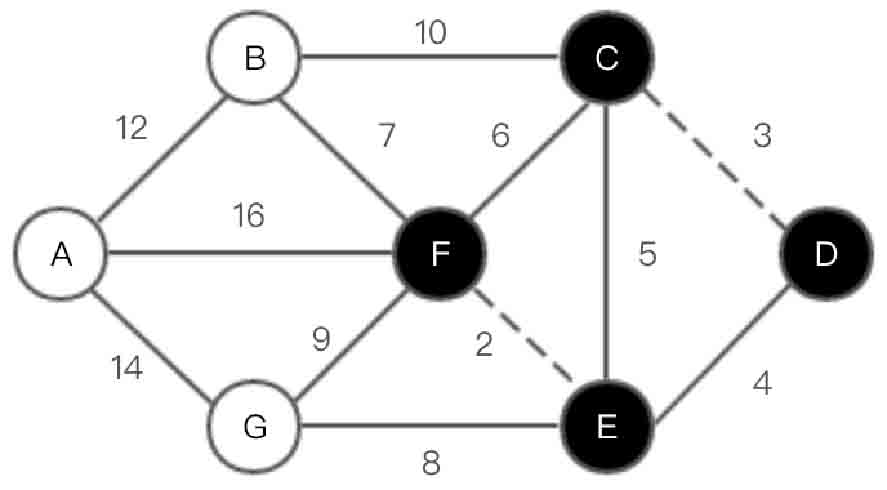
图2-144 Kruskal算法第(2)步示意图
(3)选取边<D, E>,如图2-145所示。
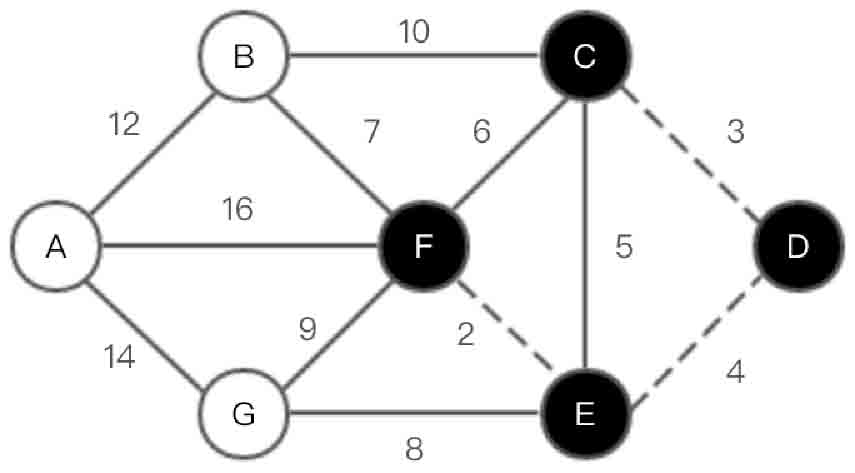
图2-145 Kruskal算法第(3)步示意图
(4)选取边<B,F>,如图2-146所示。
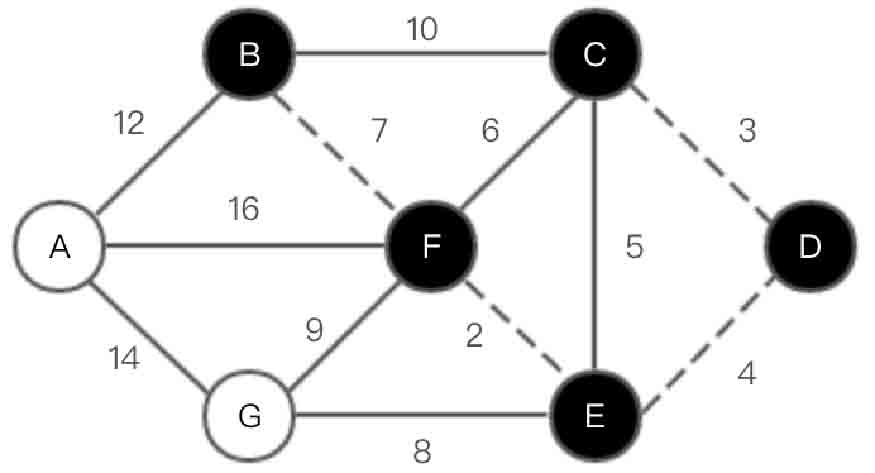
图2-146 Kruskal算法第(4)步示意图
(5)选取边<G, E>,如图2-147所示。
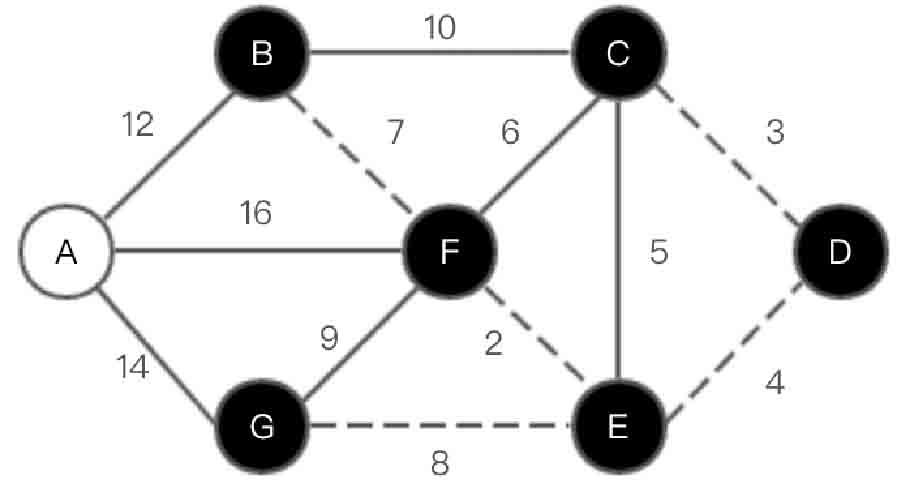
图2-147 Kruskal算法第(5)步示意图
(6)选取边<A, B>,如图2-148所示。
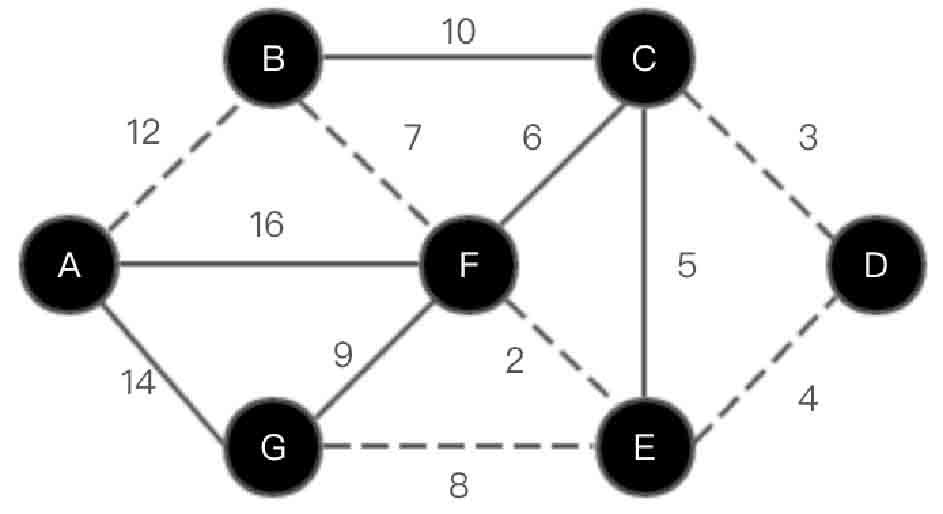
图2-148 Kruskal算法第(6)步示意图
图2-148中虚线连接的顶点和路径为最小生成树。下面通过代码实现Kruskal算法求解最小生成树,Kruskal算法求解最小生成树的实现中仍然使用Prim算法中的邻接表表示带权图,其中边用2.9.7小节介绍的EdgeData类表示。Kruskal算法实现最小生成树代码如下:
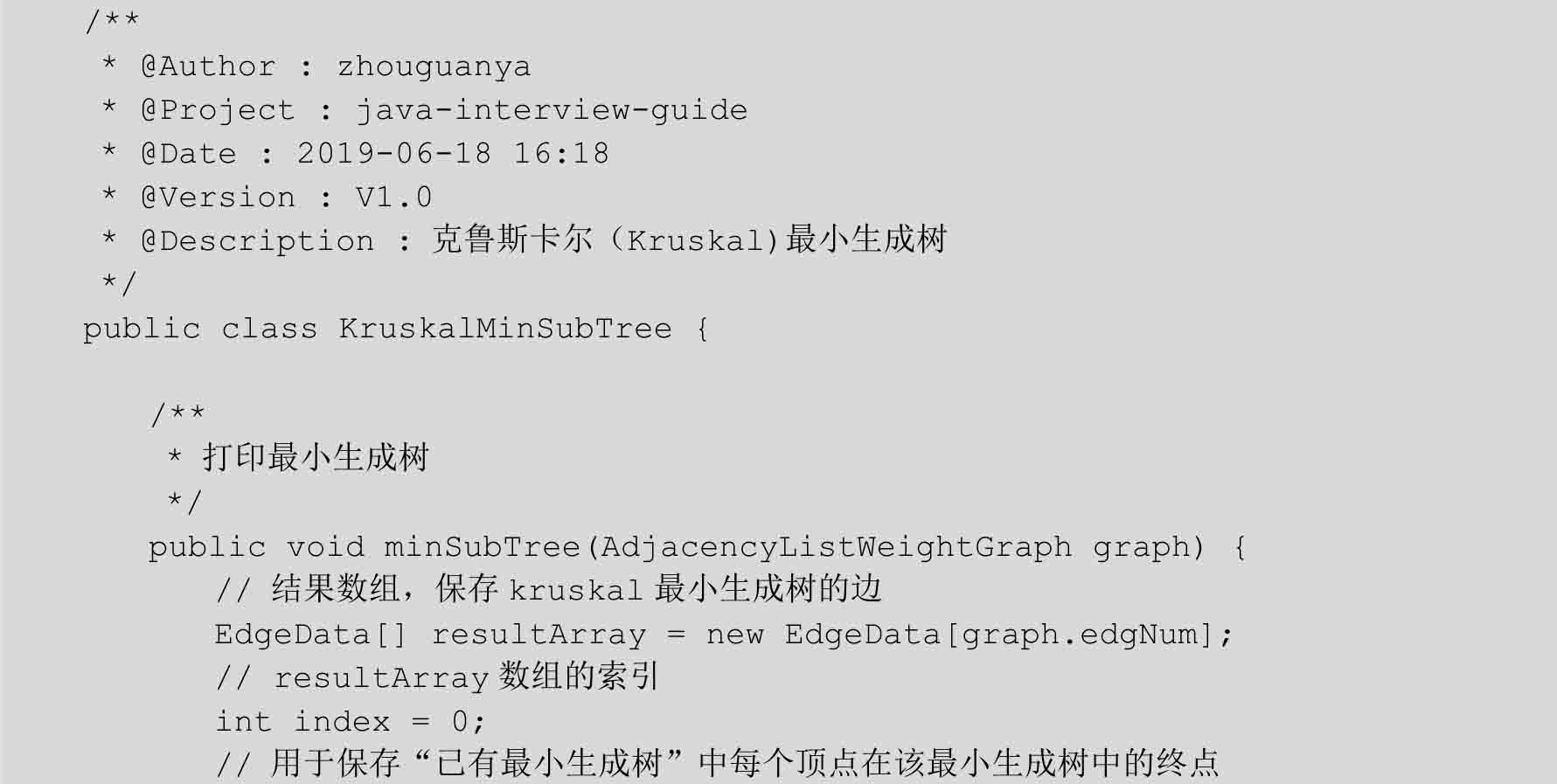



创建测试类用于验证Kruskal算法生成最小生成树的功能,测试类如下:

执行测试代码,执行结果如下:
Kruskal最小生成树=36: (E,F) (C,D) (D,E) (B,F) (E,G) (A,B)
迪杰斯特拉(Dijkstra)算法是用于计算一个顶点到其他顶点的最短路径的算法。Dijkstra的主要特点是以起始点为中心向外层扩展,直到扩展到终点为止。
通过以下案例分析Dijkstra算法求解最短路径的过程。
以图2-134为例阐述Dijkstra算法的执行过程。
(1)选取顶点D作为起点,如图2-149所示。
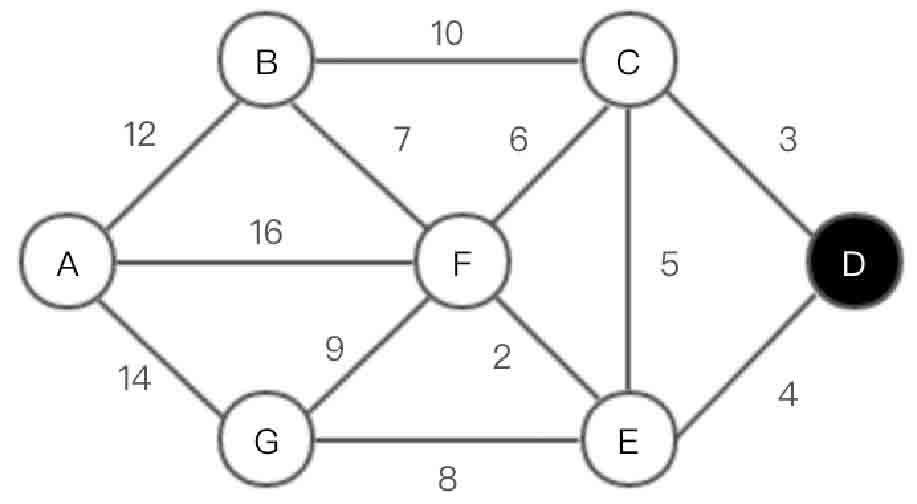
图2-149 Dijkstra算法第(1)步示意图
(2)选取顶点C,如图2-150所示。
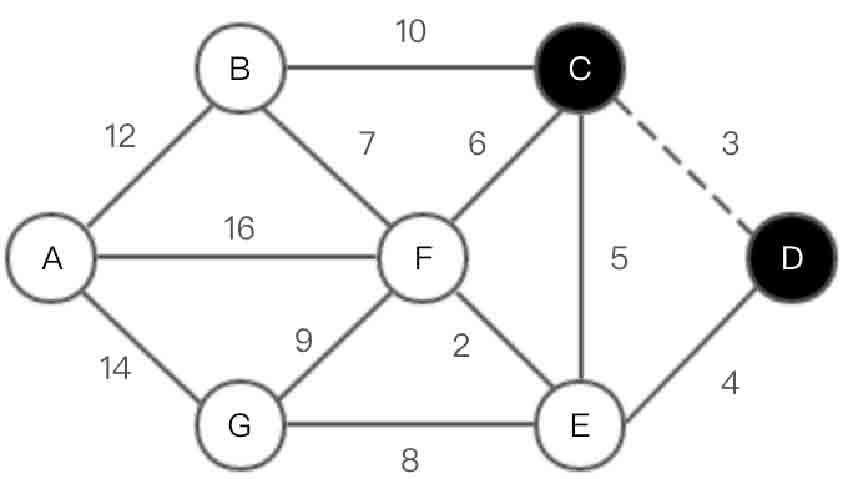
图2-150 Dijkstra算法第(2)步示意图
(3)选取顶点E,如图2-151所示。
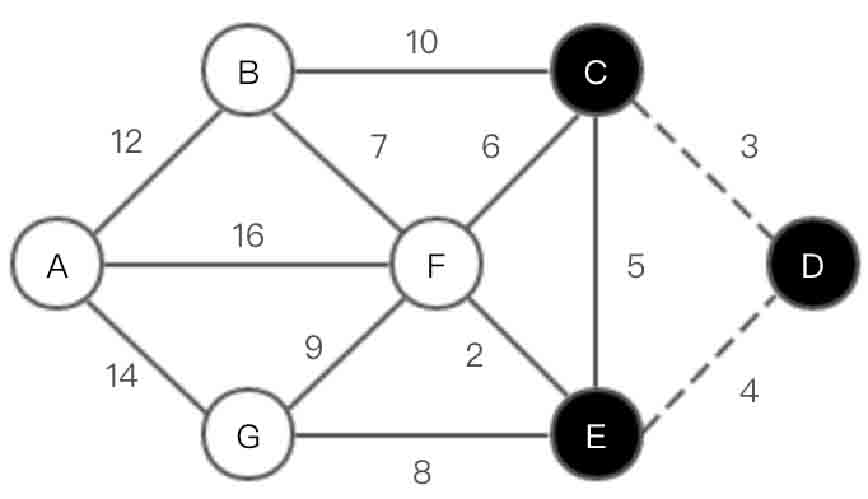
图2-151 Dijkstra算法第(3)步示意图
(4)选取顶点F,如图2-152所示。
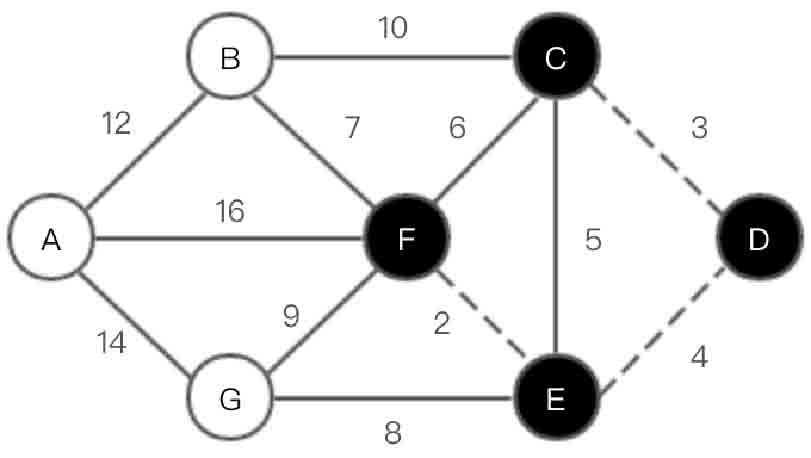
图2-152 Dijkstra算法第(4)步示意图
(5)选取顶点G,如图2-153所示。
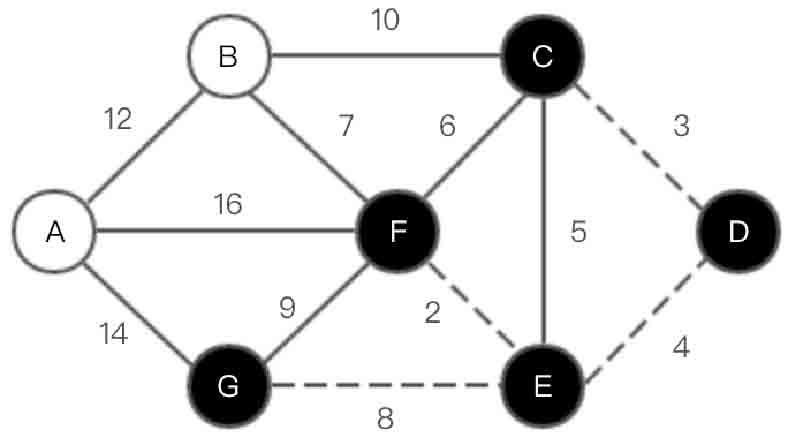
图2-153 Dijkstra算法第(5)步示意图
(6)选取顶点B,如图2-154所示。
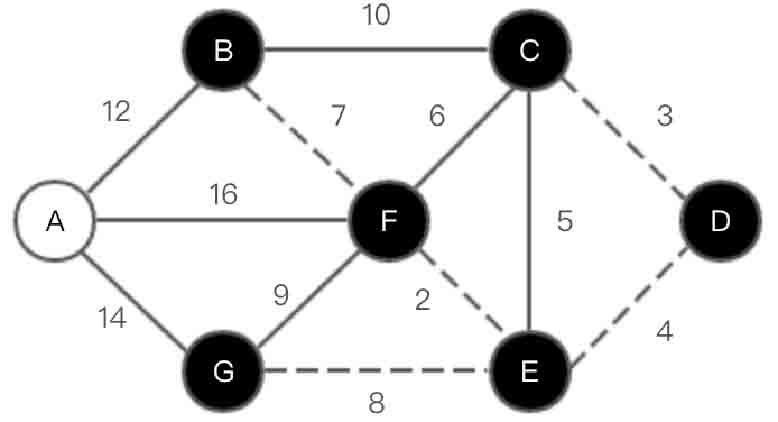
图2-154 Dijkstra算法第(6)步示意图
(7)选取顶点A,如图2-155所示。
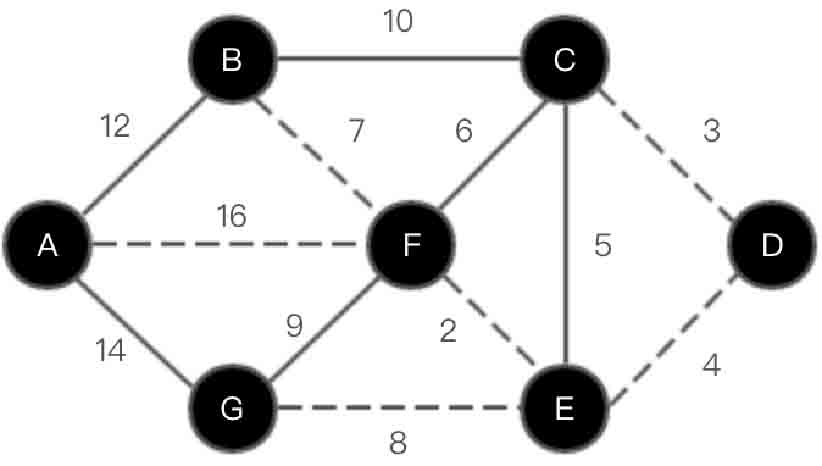
图2-155 Dijkstra算法第(7)步示意图
图2-155中虚线连接的路径为最短路径。下面通过代码实现Dijkstra算法求解最短路径,代码如下:





创建测试类用于验证Dijkstra算法生成最短路径的功能,测试类如下:

执行测试代码,执行结果如下:
dijkstra算法求解顶点D到各个顶点的最短路径:
顶点(D, A)之间的最短路径=22
顶点(D, B)之间的最短路径=13
顶点(D, C)之间的最短路径=3
顶点(D, D)之间的最短路径=0
顶点(D, E)之间的最短路径=4
顶点(D, F)之间的最短路径=6
顶点(D, G)之间的最短路径=12
(1)图的概念。
(2)图的存储方式。
(3)图的遍历方式。
(4)图的最小生成树算法。
(5)图的最短路径算法。