




《普通高中数学课程标准(2017年版)》中提出:数学运算是指在明晰运算对象的基础上,依据运算法则解决数学问题的素养.数学运算主要包括:理解运算对象、掌握运算法则、探究运算思路、选择运算方法、设计运算程序、求得运算结果等.
所谓“理解运算对象”,是指能正确区分参与运算的量,它是数学运算素养的载体.“掌握运算法则”则是指能依据确定的运算对象采取正确的运算方法和规则,它的作用是保证运算结果的唯一性.“运算思路”的合理与否在数学运算中起到至关重要的作用,是解决数学问题的关键,是数学运算素养的精华.“运算程序”则是运算方法的具体化,是解决一类问题可操作的步骤,也是借助外界力量解决问题的路线图.由此可见,参与数学运算的过程,实际上是思维整理和提炼的过程,是思维品质的体现.
数学运算素养的具体表现是:理解数和式的有关算理;能够根据法则准确地进行运算、变形;能够根据条件寻找与设计合理、简捷的运算途径;能够通过运算对问题进行推理和探求.
1.教材分析
对数及其运算是在学习指数与指数函数及其性质的基础上,引入对数的概念,探讨对数的运算性质.本节学习的内容蕴含转化与化归的数学思想、类比与对比等基本数学方法,为以后进一步学习对数函数打下基础.
2.“对数及其运算”中的数学运算素养要求
(1)理解对数的概念,了解对底数和真数的要求.
(2)理解对数的运算性质,知道用换底公式能将一般对数转化为自然对数或常用对数.
(3)在教师的引导下,通过课堂学习活动培养学生自主探究与合作交流的学习习惯,提升指对数互相转化以及对数基本运算的能力,且在相互交流的过程中养成学生表述、归纳的思维习惯,进而获得成功的体验.
(4)经历和体验数学运算的活动的过程,培养学生对待知识的科学态度、勇于探索和创新的精神,让学生在质疑、交流、合作过程中获得发现的成就感,激发学生学习数学知识的兴趣,形成良好的数学思维品质.在民主、和谐的教学气氛中,促进师生的情感交流.
3.教学过程设计
教学过程设计(对数的运算性质部分)见表2-1.
表2-1

4.课后反思
通过几个“你发现了什么”进一步引导学生开展思维活动,课堂实践中贯穿了数学运算素养,通过计算、猜想、推导、论证,学生们的运算能力得到了真正的提高,同时形成了关于对数的概念和运算更加深刻的理解和记忆.
如果说概念的内涵是指概念所反映的特性和本质属性,那么外延则是指概念所反映对象的具体范围或者所指的事物所组成的那个类.数学运算素养是运用运算法则解决数学问题的素养,那么它的外延可以表述为在明晰对象的基础上,依据相应的法则解决问题的素养,也就是适合这个概念的一切对象.如矩形、正方形、菱形以及其他平行四边形都是平行四边形这一概念的外延.
数学运算素养的外延表现形式有数学运算方法、运算技巧等的深化和细分;与其他素养和能力的互相融合;和其他学科之间的兼容等,在实际问题处理的过程中,要注意突破运算相关的表象,透彻理解其本质特征.如曲线中的弦长其实就是两点之间距离的延伸.当然,数学运算的外延还可以是从数学的领域向非数学的领域延伸.如通过对事物的估算,开展合理性研究等.
因式分解的概念在有理数域、实数域、复数域各有不同,教师在授课时不宜把它说成一成不变的概念或公式,建议留有余地,以便随着学生数学知识的延拓而改变.
问题: 分解因式 x 4 -4.
i在有理数域中: x 4 -4=( x 2 -2)( x 2 +2).
ii在实数域中:
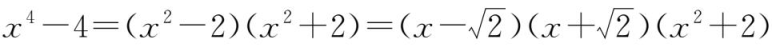 .
.
iii在复数域中:
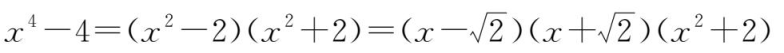
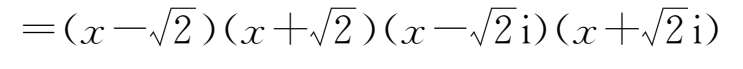
数学运算主要表现为:理解运算对象、掌握运算法则、探究运算思路、求得运算结果.这是一个有机整体,在解决问题中相辅相成.
理解运算对象的含义和作用至关重要,高中阶段学生需要掌握几种重要的运算对象:数、字母(代数式)、向量、矩阵、行列式等.不仅要求学生会进行相应的运算,还要理解它们的作用.
问题:
对满足-1≤
a
≤1的一切
a
的值,都有
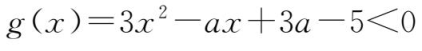 ,求实数
x
的取值范围.
,求实数
x
的取值范围.
角度1 本题是含有双变量的不等式问题,属于恒成立问题的范畴.学生们出于习惯,喜欢把 x 当做变量,将本题视为关于 x 的一元二次不等式问题,于是解决这个问题需要应用二次函数以及二次方程实根分布,有点麻烦,可以尝试利用变量分离的方法解决.
解 问题等价于 a (3- x )<5-3 x 2 在-1≤ a ≤1时恒成立,
i当
x
<3时
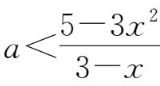 在-1≤
a
≤1时恒成立,所以
在-1≤
a
≤1时恒成立,所以
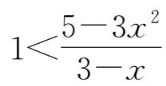 .
.
ii当 x =3时,0<-22矛盾,所以 x ≠3.
iii当
x
>3时,
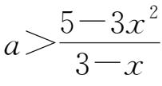 在-1≤
a
≤1时恒成立,所以
在-1≤
a
≤1时恒成立,所以
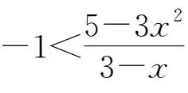 .
.
综上可得,
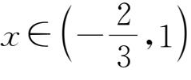 .
.
角度2 常量与变量是相对的,一般地,可把已知范围的那个量看作自变量,另一个量看作常量.因此,如果把 x 与 a 互换一下,即将 a 视为变量, x 视为常量,则上述问题可以转化为在[-1,1]内关于 a 的一次式小于0恒成立问题.
解 令 h ( a )=(3- x ) a +3 x 2 -5,-1≤ a ≤1
对-1≤ a ≤1,恒有 g ( x )<0,即 h ( a )<0.
所以
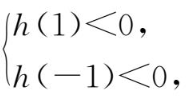 即
即
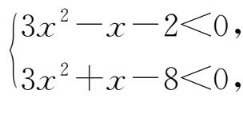
解得
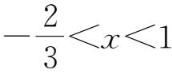 .故
x
的取值范围为
.故
x
的取值范围为
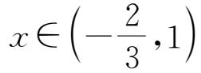 .
.
运算法则是运算的依据,是推理的基础,也是运算结果具有唯一性的保障.在数学运算解决问题的过程中,运算法则可以帮助我们提供运算思路.