




方法2中标量积矩阵的构造方式与方法1中的有所不同。首先令
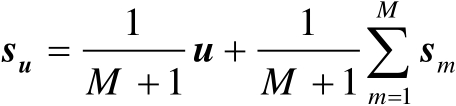
(4.42)
利用传感器和辐射源的位置向量定义如下坐标矩阵
 :
:
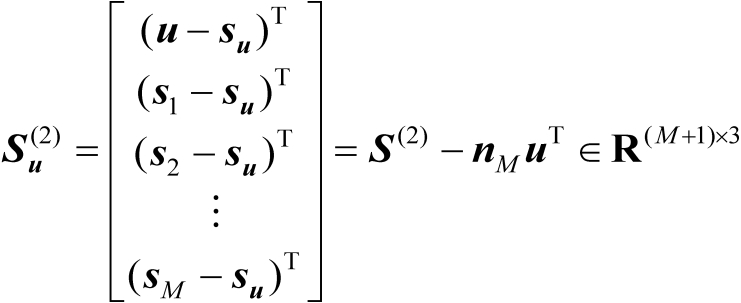
(4.43)
式中
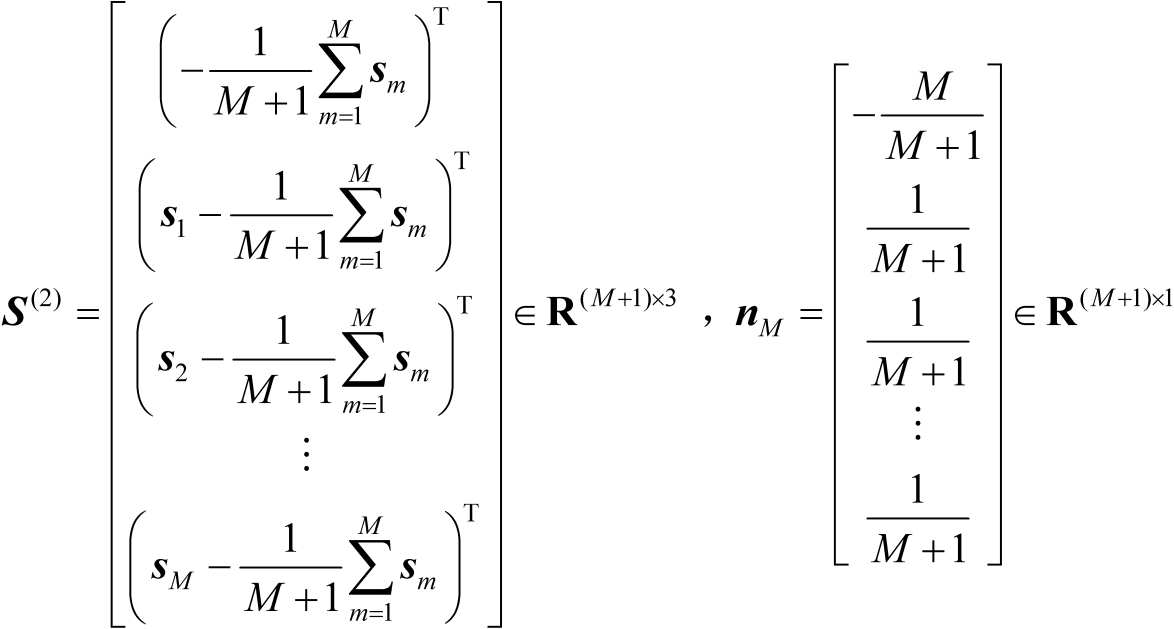
(4.44)
假设
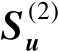 为列满秩矩阵,即有
为列满秩矩阵,即有
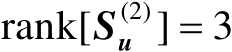 。然后构造如下标量积矩阵:
。然后构造如下标量积矩阵:
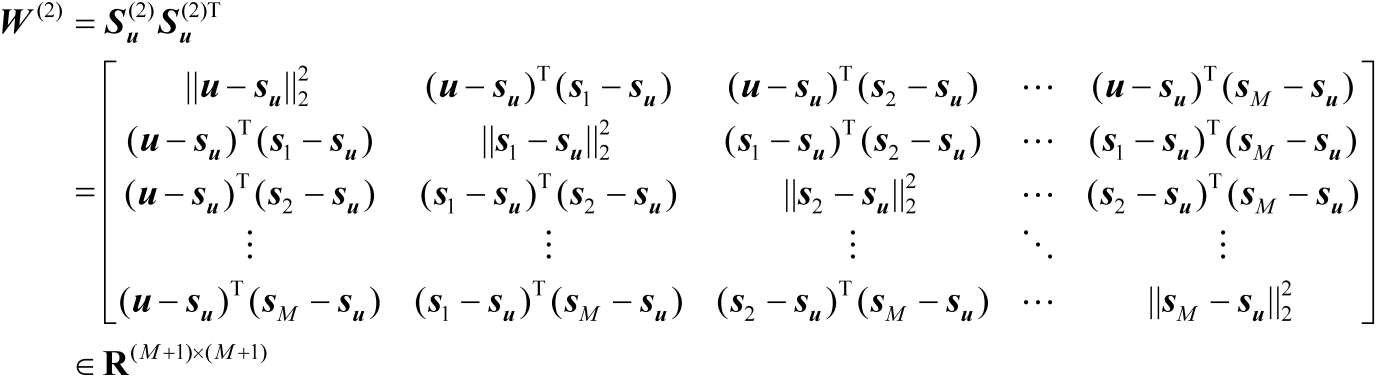
(4.45)
根据命题2.12可知,矩阵
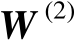 可以表示为
可以表示为
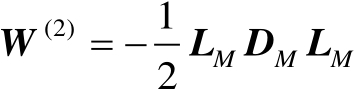
(4.46)
式中
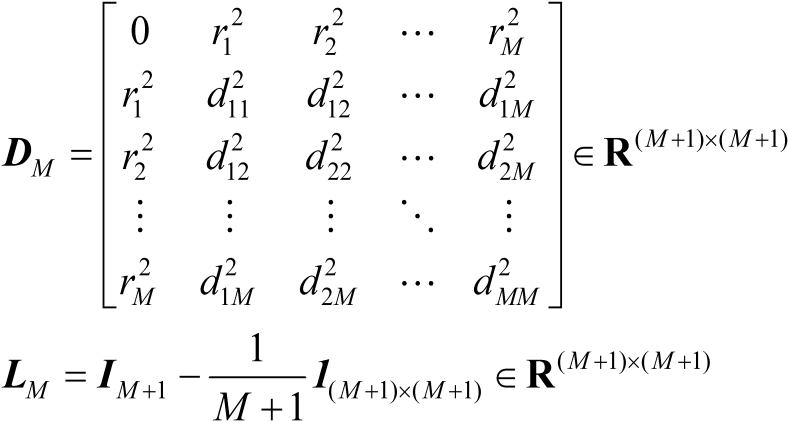
(4.47)
式(4.46)和式(4.47)提供了构造矩阵
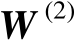 的计算公式,相比于方法1中的标量积矩阵
的计算公式,相比于方法1中的标量积矩阵
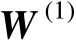 ,方法2中的标量积矩阵
,方法2中的标量积矩阵
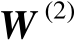 的阶数增加了1维。现对矩阵
的阶数增加了1维。现对矩阵
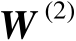 进行特征值分解可得
进行特征值分解可得
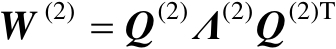
(4.48)
式中,
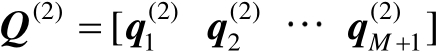 为特征向量构成的矩阵;
为特征向量构成的矩阵;
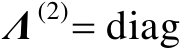
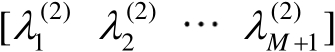 为特征值构成的对角矩阵,并且假设
为特征值构成的对角矩阵,并且假设
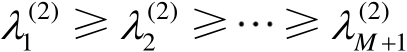 。由于
。由于
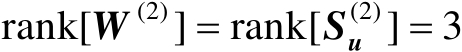 ,则有
,则有
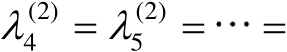
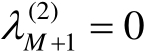 。若令
。若令
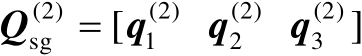 、
、
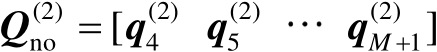 及
及
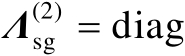
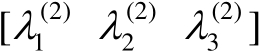 ,则可以将矩阵
,则可以将矩阵
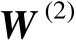 表示为
表示为
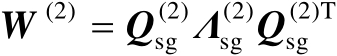
(4.49)
再利用特征向量之间的正交性可得
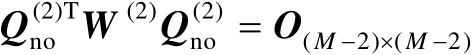
(4.50)
【注记4.5】
本章将矩阵
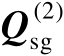 的列空间称为信号子空间(
的列空间称为信号子空间(
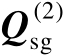 也称为信号子空间矩阵),将矩阵
也称为信号子空间矩阵),将矩阵
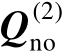 的列空间称为噪声子空间(
的列空间称为噪声子空间(
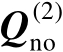 也称为噪声子空间矩阵)。
也称为噪声子空间矩阵)。
类似于命题4.1,这里可以得到如下结论。
【命题4.3】
假设
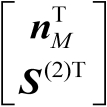 是行满秩矩阵,则有
是行满秩矩阵,则有
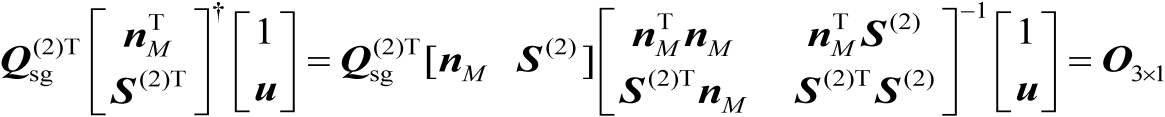
(4.51)
命题4.3的证明与命题4.1的证明类似,限于篇幅这里不再重复阐述。式(4.51)给出的关系式至关重要,但并不是最终的关系式。将式(4.51)两边左乘以
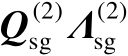 可得
可得
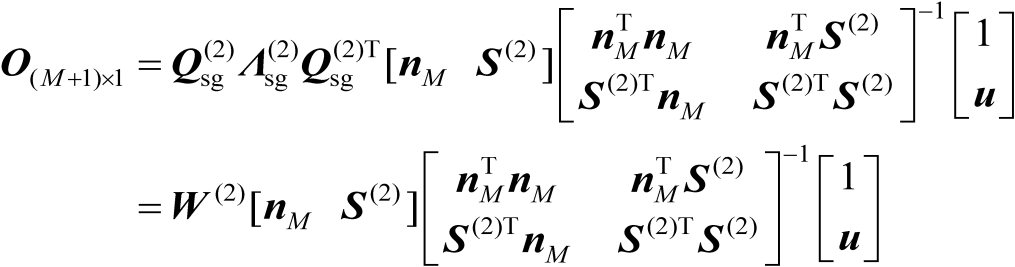
(4.52)
式中,第2个等号处的运算利用了式(4.49)。式(4.52)即为最终确定的关系式,它建立了关于辐射源位置向量
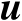 的伪线性等式,其中一共包含
的伪线性等式,其中一共包含
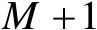 个等式,而TOA观测量仅为
个等式,而TOA观测量仅为
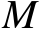 个,这意味着该关系式是存在冗余的。
个,这意味着该关系式是存在冗余的。
下面将基于式(4.52)构建确定辐射源位置向量
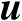 的估计准则,并且推导其最优解。为了简化数学表述,首先定义如下矩阵和向量:
的估计准则,并且推导其最优解。为了简化数学表述,首先定义如下矩阵和向量:
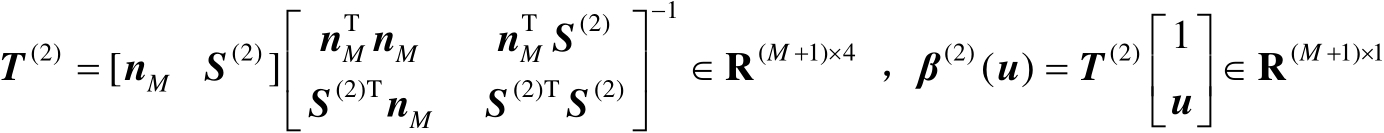
(4.53)
结合式(4.52)和式(4.53)可得
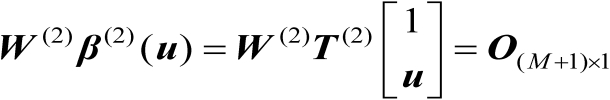
(4.54)
1.一阶误差扰动分析
在实际定位过程中,标量积矩阵
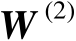 的真实值是未知的,因为其中的真实距离
的真实值是未知的,因为其中的真实距离
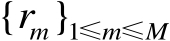 仅能用其观测值
仅能用其观测值
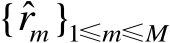 来代替,这必然会引入观测误差。不妨将含有观测误差的标量积矩阵
来代替,这必然会引入观测误差。不妨将含有观测误差的标量积矩阵
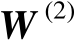 记为
记为
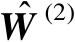 ,于是利用式(4.46)和式(4.47)可知,矩阵
,于是利用式(4.46)和式(4.47)可知,矩阵
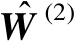 可以表示为
可以表示为
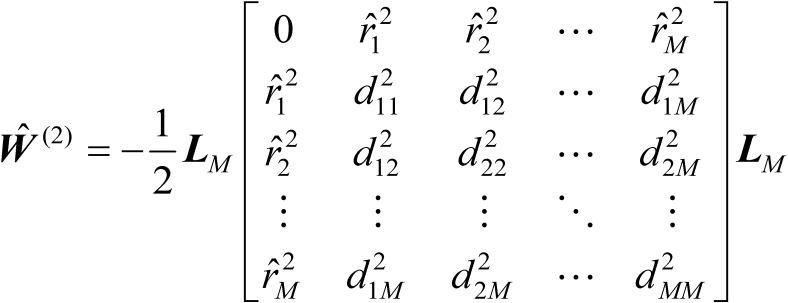
(4.55)
由于
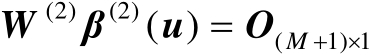 ,于是可以定义如下误差向量:
,于是可以定义如下误差向量:
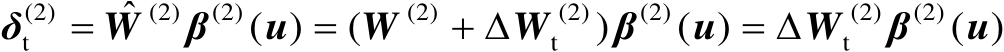
(4.56)
式中,
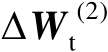 表示
表示
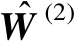 中的误差矩阵,即有
中的误差矩阵,即有
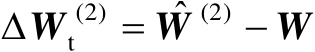 。若忽略观测误差
。若忽略观测误差
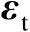 的二阶及其以上各阶项,根据式(4.55)可以将误差矩阵
的二阶及其以上各阶项,根据式(4.55)可以将误差矩阵
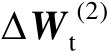 近似表示为
近似表示为

(4.57)
将式(4.57)代入式(4.56)中可以将误差向量
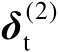 近似表示为关于观测误差
近似表示为关于观测误差
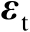 的线性函数,如下式所示:
的线性函数,如下式所示:
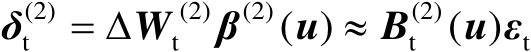
(4.58)
式中
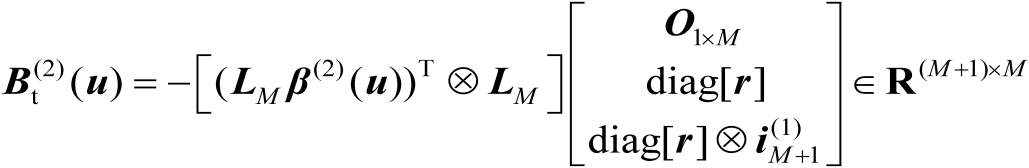
(4.59)
式(4.58)的推导见附录A.3。由式(4.58)可知,误差向量
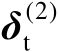 渐近服从零均值的高斯分布,并且其协方差矩阵为
渐近服从零均值的高斯分布,并且其协方差矩阵为
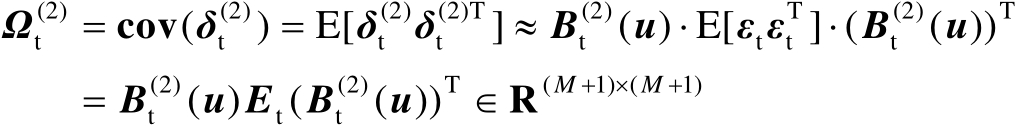
(4.60)
2.定位优化模型及其求解方法
一般而言,矩阵
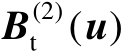 是列满秩的,即有
是列满秩的,即有
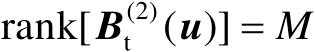 。由此可知,协方差矩阵
。由此可知,协方差矩阵
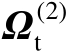 的秩也为
的秩也为
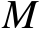 ,但由于
,但由于
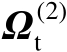 是
是
 阶方阵,这意味着它是秩亏损矩阵,所以无法直接利用该矩阵的逆构建估计准则。下面利用矩阵奇异值分解重新构造误差向量,以使其协方差矩阵具备满秩性。
阶方阵,这意味着它是秩亏损矩阵,所以无法直接利用该矩阵的逆构建估计准则。下面利用矩阵奇异值分解重新构造误差向量,以使其协方差矩阵具备满秩性。
首先对矩阵
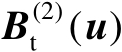 进行奇异值分解,如下式所示:
进行奇异值分解,如下式所示:
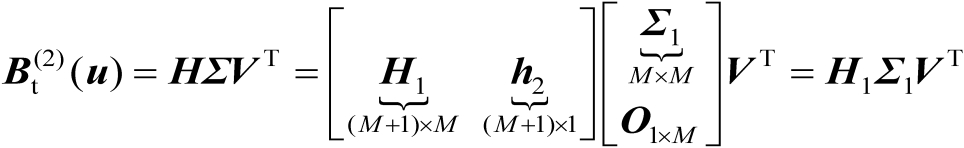
(4.61)
式中,
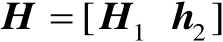 为
为
 阶正交矩阵;
阶正交矩阵;
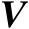 为
为
 阶正交矩阵;
阶正交矩阵;
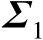 为
为
 阶对角矩阵,其中的对角元素为矩阵
阶对角矩阵,其中的对角元素为矩阵
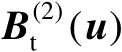 的奇异值。为了得到协方差矩阵为满秩的误差向量,可以将矩阵
的奇异值。为了得到协方差矩阵为满秩的误差向量,可以将矩阵
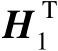 左乘以误差向量
左乘以误差向量
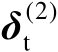 ,并结合式(4.56)和式(4.58)可得
,并结合式(4.56)和式(4.58)可得
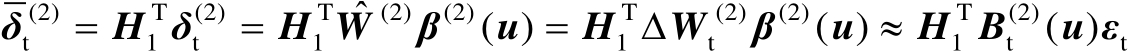
(4.62)
由式(4.61)可得
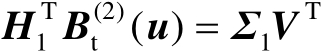 ,将该式代入式(4.62)中可知,误差向量
,将该式代入式(4.62)中可知,误差向量
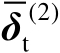 的协方差矩阵为
的协方差矩阵为
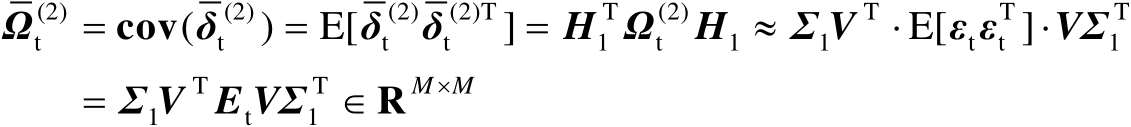
(4.63)
容易验证
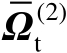 为满秩矩阵,并且误差向量
为满秩矩阵,并且误差向量
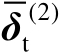 的维数为
的维数为
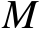 ,其与TOA观测量个数相等,此时可以将估计辐射源位置向量
,其与TOA观测量个数相等,此时可以将估计辐射源位置向量
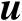 的优化准则表示为
的优化准则表示为
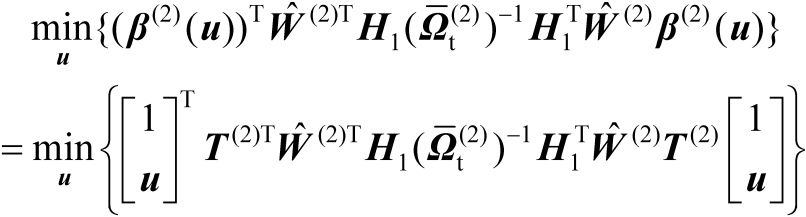
(4.64)
式中,
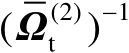 可以看作加权矩阵,其作用在于抑制观测误差
可以看作加权矩阵,其作用在于抑制观测误差
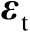 的影响。不妨将矩阵
的影响。不妨将矩阵
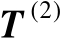 分块表示为
分块表示为
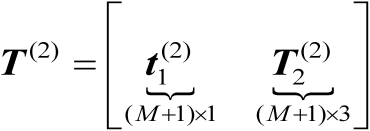
(4.65)
则可以将式(4.64)重新写为
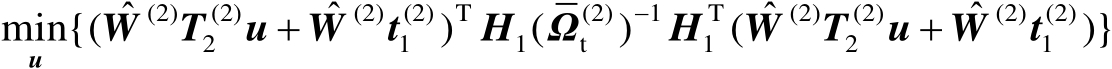
(4.66)
根据命题2.13可知,式(4.66)的最优解为
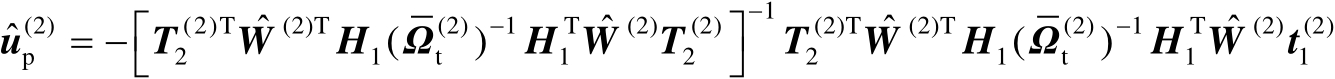
(4.67)
【注记4.6】
由式(4.60)、式(4.61)及式(4.63)可知,加权矩阵
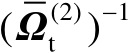 与辐射源位置向量
与辐射源位置向量
 有关。因此,严格来说,式(4.66)中的目标函数并不是关于向量
有关。因此,严格来说,式(4.66)中的目标函数并不是关于向量
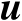 的二次函数,针对该问题,可以采用注记4.1中描述的方法进行处理。理论分析表明,在一阶误差分析理论框架下,加权矩阵
的二次函数,针对该问题,可以采用注记4.1中描述的方法进行处理。理论分析表明,在一阶误差分析理论框架下,加权矩阵
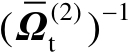 中的扰动误差并不会实质影响估计值
中的扰动误差并不会实质影响估计值
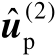 的统计性能。
的统计性能。
图4.8给出了本章第2种加权多维标度定位方法的流程图。
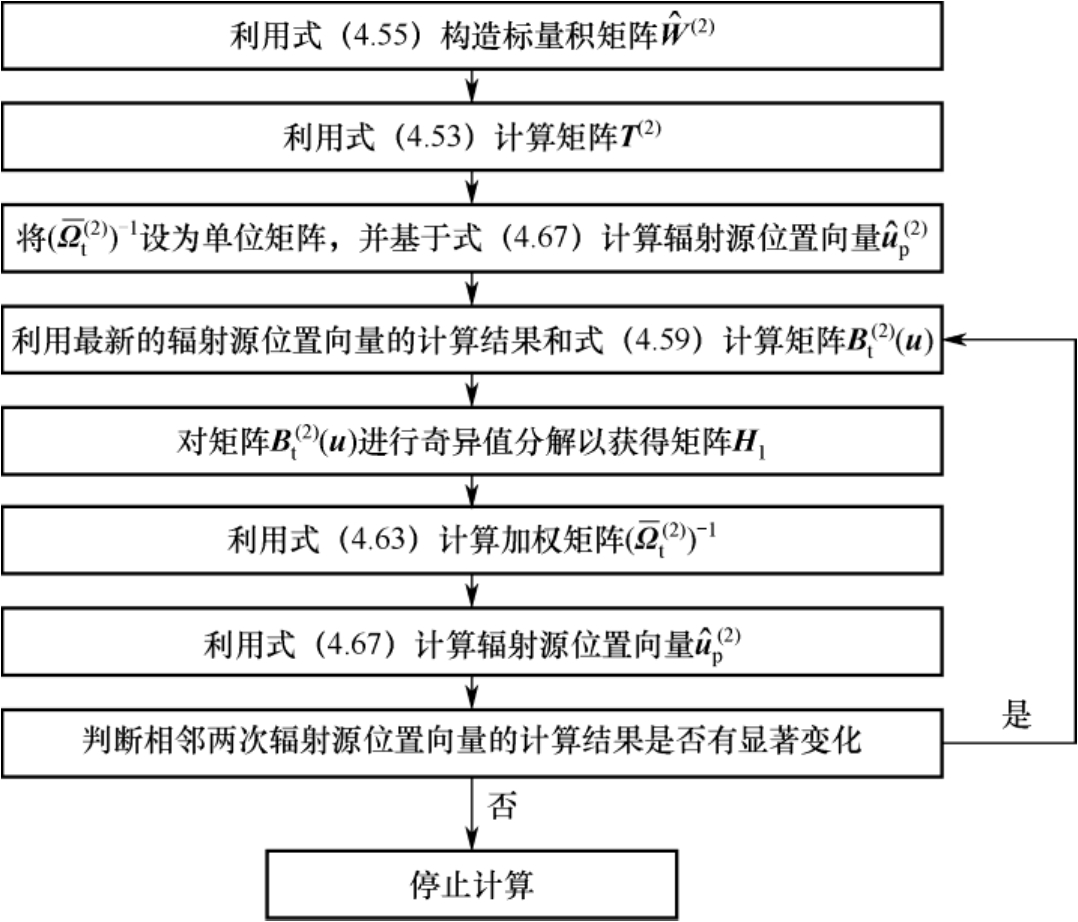
图4.8 本章第2种加权多维标度定位方法的流程图
下面将推导估计值
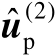 的理论性能,主要是推导估计均方误差矩阵,并将其与相应的克拉美罗界进行比较,从而证明其渐近最优性。这里采用的性能分析方法是一阶误差分析方法,即忽略观测误差
的理论性能,主要是推导估计均方误差矩阵,并将其与相应的克拉美罗界进行比较,从而证明其渐近最优性。这里采用的性能分析方法是一阶误差分析方法,即忽略观测误差
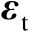 的二阶及其以上各阶项。
的二阶及其以上各阶项。
首先将最优解
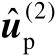 中的估计误差记为
中的估计误差记为
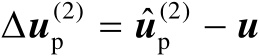 。基于式(4.67)和注记4.6中的讨论可知
。基于式(4.67)和注记4.6中的讨论可知
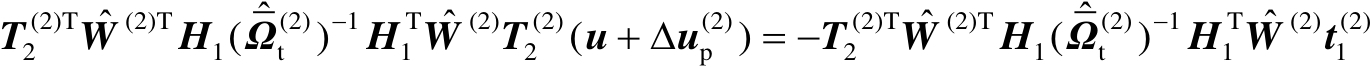
(4.68)
式中,
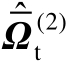 表示
表示
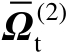 的估计值。在一阶误差分析框架下,基于式(4.68)可以进一步推得
的估计值。在一阶误差分析框架下,基于式(4.68)可以进一步推得
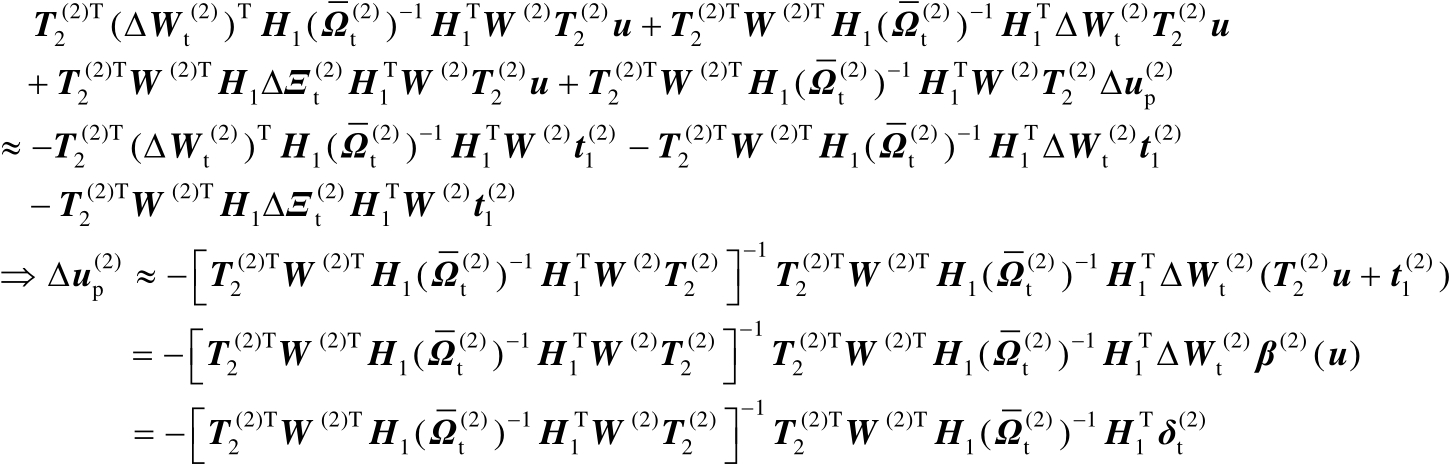
(4.69)
式中,
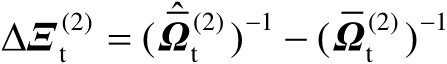 ,表示矩阵
,表示矩阵
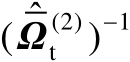 中的扰动误差。由式(4.69)可知,估计误差
中的扰动误差。由式(4.69)可知,估计误差
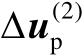 渐近服从零均值的高斯分布,因此估计值
渐近服从零均值的高斯分布,因此估计值
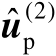 是渐近无偏估计,并且其均方误差矩阵为
是渐近无偏估计,并且其均方误差矩阵为
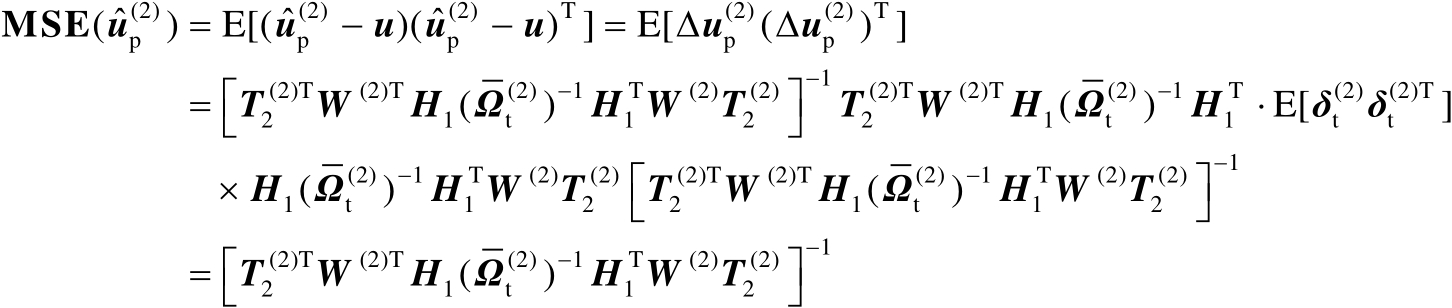
(4.70)
【注记4.7】
式(4.69)再次表明,在一阶误差分析理论框架下,矩阵
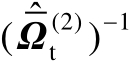 中的扰动误差
中的扰动误差
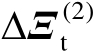 并不会实质影响估计值
并不会实质影响估计值
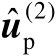 的统计性能。
的统计性能。
下面证明估计值
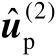 具有渐近最优性,也就是证明其估计均方误差矩阵可以渐近逼近相应的克拉美罗界,具体可见如下命题。
具有渐近最优性,也就是证明其估计均方误差矩阵可以渐近逼近相应的克拉美罗界,具体可见如下命题。
【命题4.4】
在一阶误差分析理论框架下,
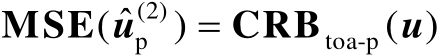 。
。
【证明】 首先将式(4.63)代入式(4.70)中可得
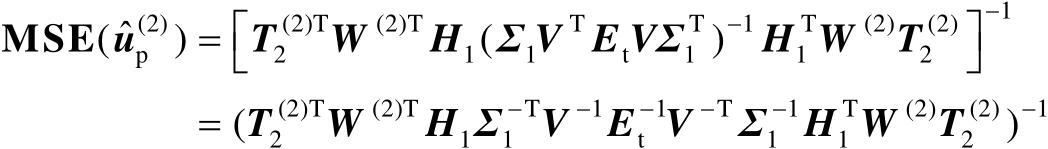
(4.71)
对比式(4.37)和式(4.71)可知,下面仅需要证明
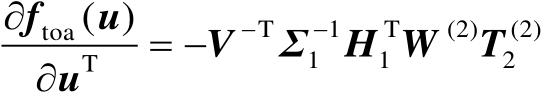
(4.72)
考虑等式
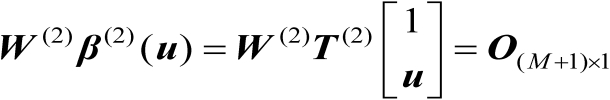 ,将该等式两边对向量
,将该等式两边对向量
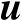 求导可知
求导可知
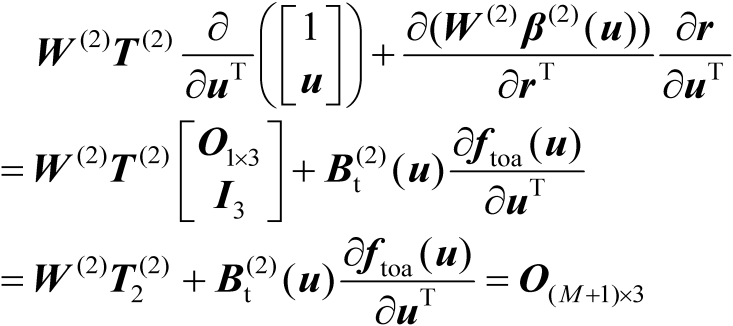
(4.73)
再用矩阵
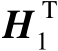 左乘以式(4.73)两边可得
左乘以式(4.73)两边可得
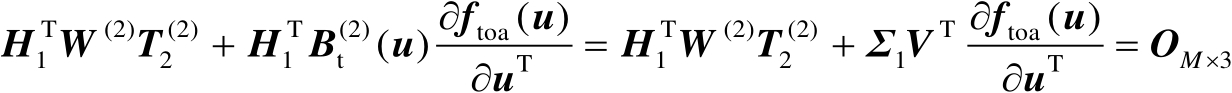
(4.74)
由式(4.74)可知式(4.72)成立。证毕。
假设利用6个传感器获得的TOA信息(也即距离信息)对辐射源进行定位,传感器三维位置坐标如表4.2所示,距离观测误差
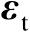 服从均值为零、协方差矩阵为
服从均值为零、协方差矩阵为
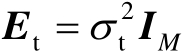 的高斯分布。
的高斯分布。
表4.2 传感器三维位置坐标 (单位:m)

首先将辐射源位置向量设为
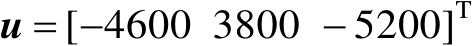 (m),将标准差设为
(m),将标准差设为
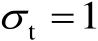 ,图4.9给出了定位结果散布图与定位误差椭圆曲线;图4.10给出了定位结果散布图与误差概率圆环曲线。
,图4.9给出了定位结果散布图与定位误差椭圆曲线;图4.10给出了定位结果散布图与误差概率圆环曲线。
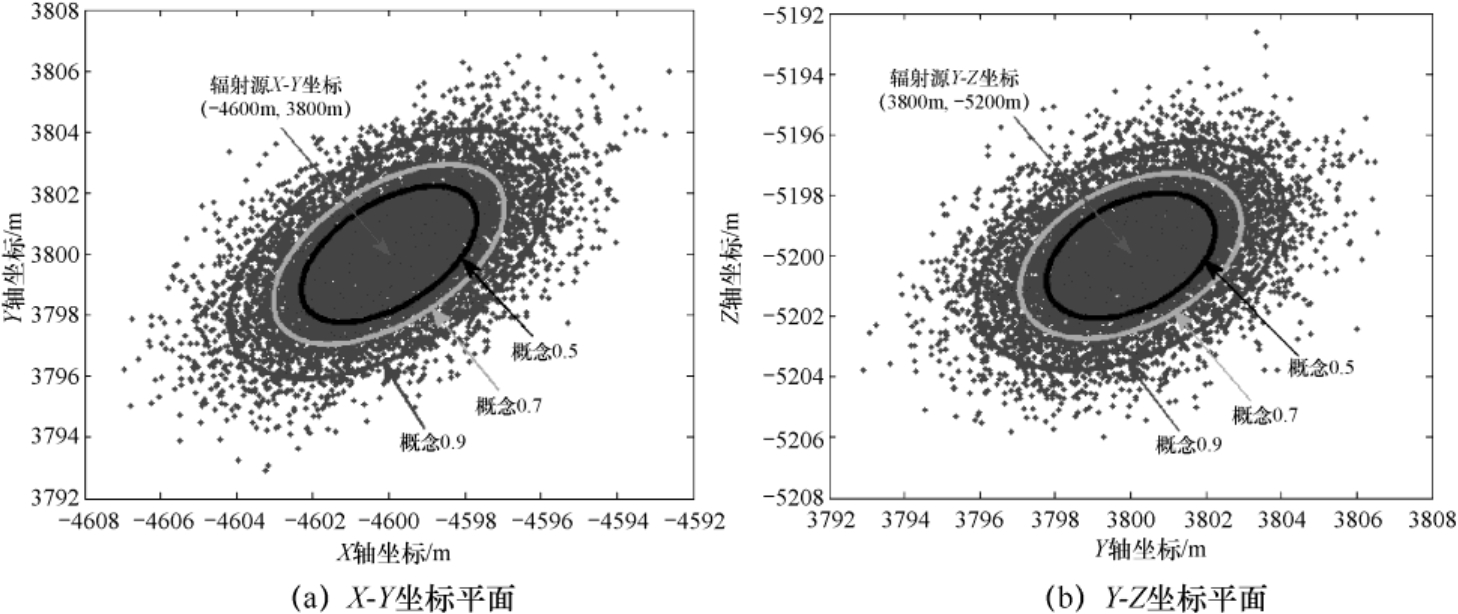
图4.9 定位结果散布图与定位误差椭圆曲线
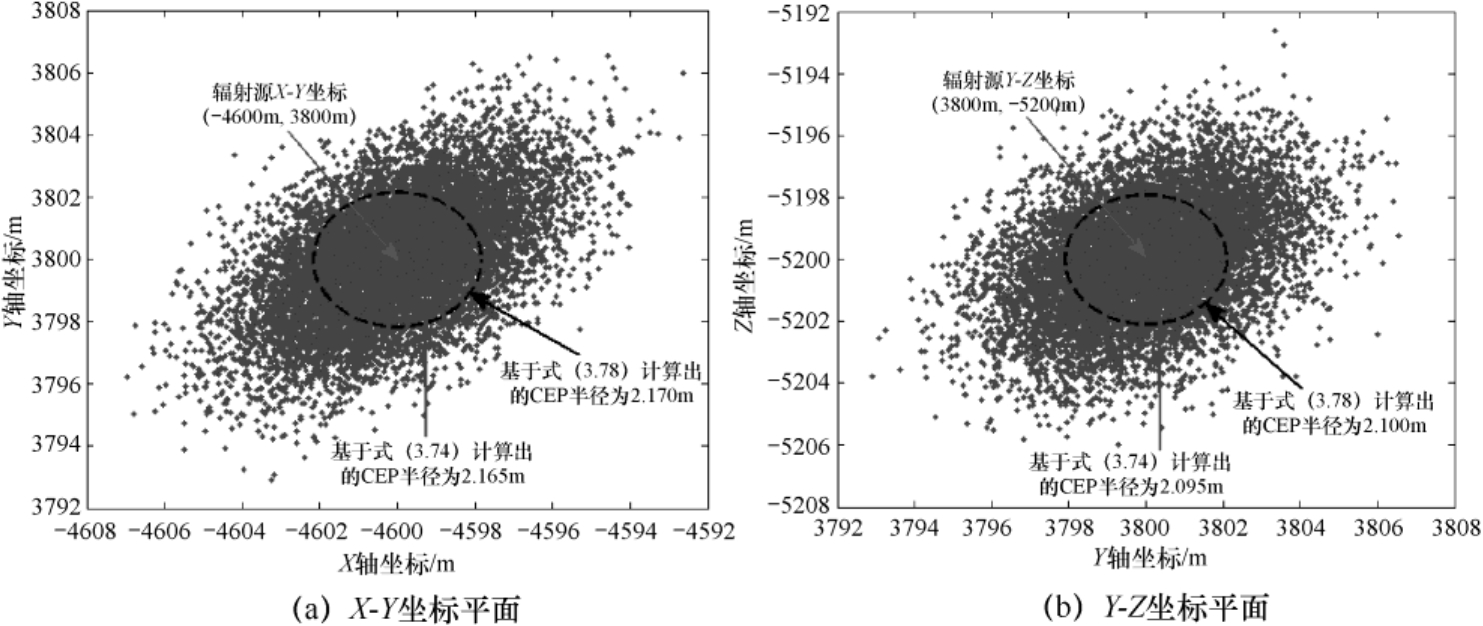
图4.10 定位结果散布图与误差概率圆环曲线
然后将辐射源坐标设为两种情形:第1种是近场源,其位置向量为
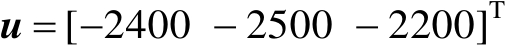 (m);第2种是远场源,其位置向量为
(m);第2种是远场源,其位置向量为
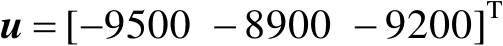 (m)。改变标准差
(m)。改变标准差
 的数值,图4.11给出了辐射源位置估计均方根误差随着标准差
的数值,图4.11给出了辐射源位置估计均方根误差随着标准差
 的变化曲线;图4.12给出了辐射源定位成功概率随着标准差
的变化曲线;图4.12给出了辐射源定位成功概率随着标准差
 的变化曲线(图中的理论值是根据式(3.29)和式(3.36)计算得出的,其中
的变化曲线(图中的理论值是根据式(3.29)和式(3.36)计算得出的,其中
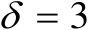 m)。
m)。
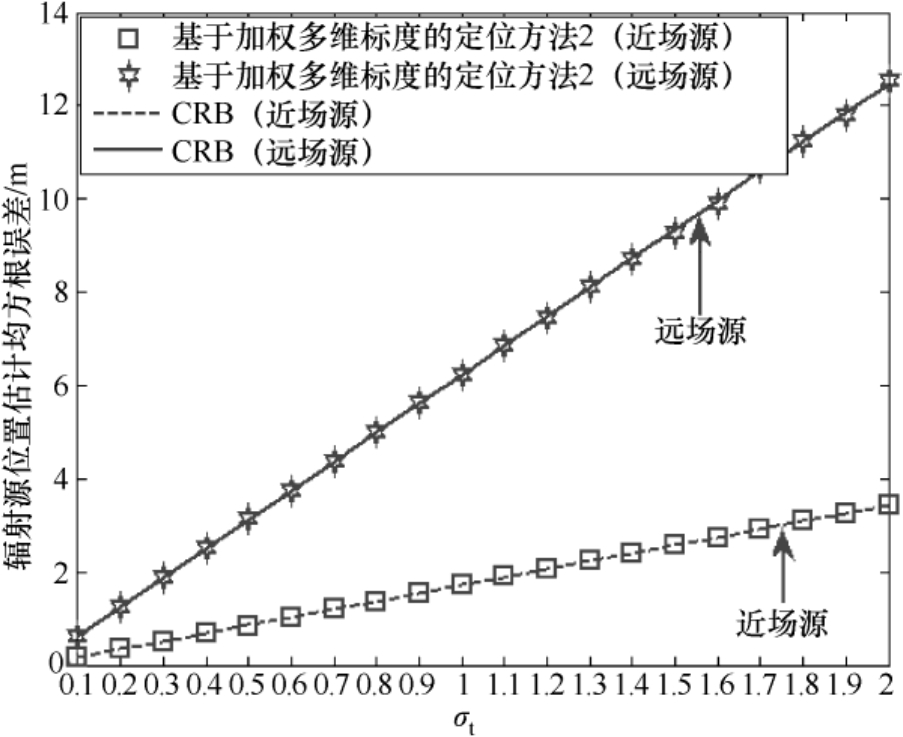
图4.11 辐射源位置估计均方根误差随着标准差 σ t 的变化曲线
最后将标准差
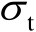 设为两种情形:第1种是
设为两种情形:第1种是
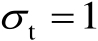 ;第2种是
;第2种是
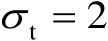 ,将辐射源位置向量设为
,将辐射源位置向量设为
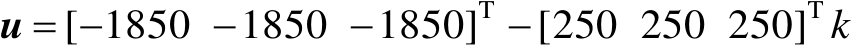 (m)。改变参数
(m)。改变参数
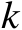 的数值,图4.13给出了辐射源位置估计均方根误差随着参数
的数值,图4.13给出了辐射源位置估计均方根误差随着参数
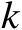 的变化曲线;图4.14给出了辐射源定位成功概率随着参数
的变化曲线;图4.14给出了辐射源定位成功概率随着参数
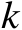 的变化曲线(图中的理论值是根据式(3.29)和式(3.36)计算得出的,其中
的变化曲线(图中的理论值是根据式(3.29)和式(3.36)计算得出的,其中
 m)。
m)。
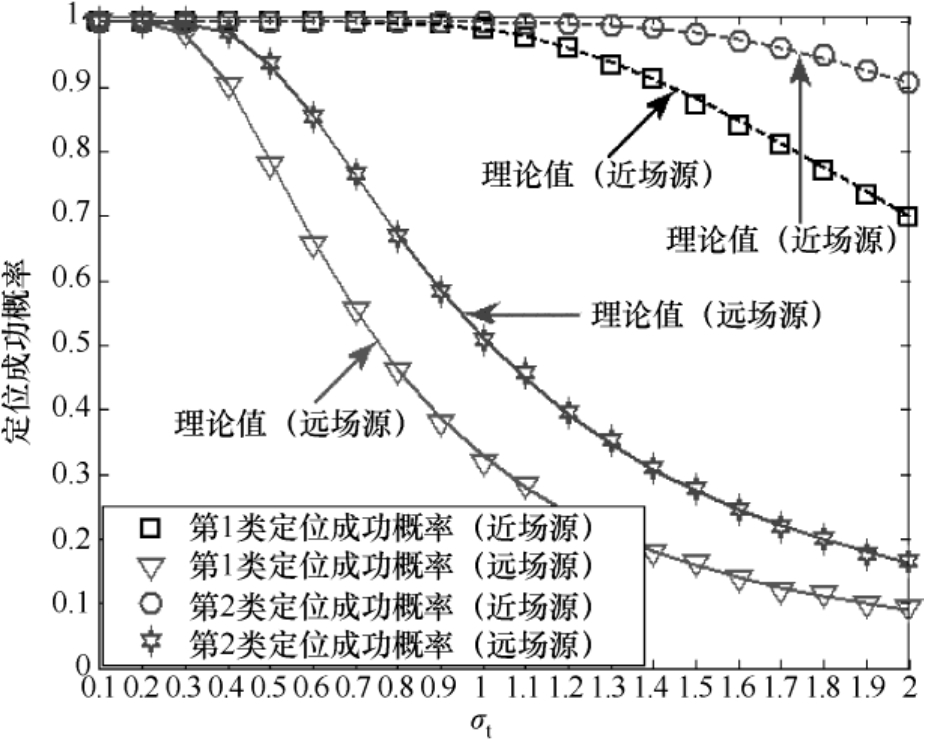
图4.12 辐射源定位成功概率随着标准差 σ t 的变化曲线
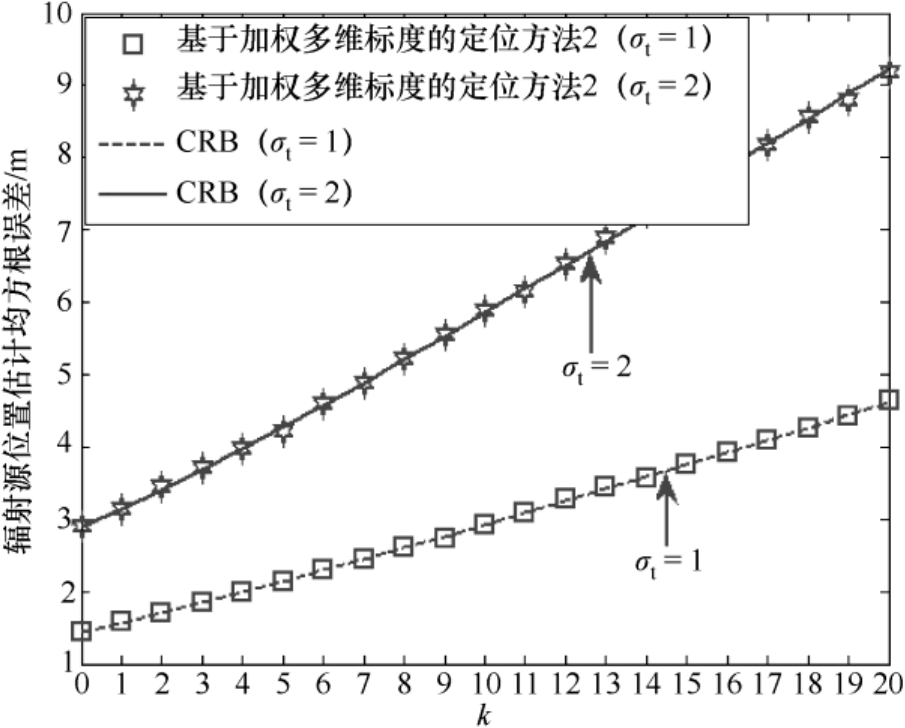
图4.13 辐射源位置估计均方根误差随着参数 k 的变化曲线
从图4.11~图4.14中可以看出:(1)基于加权多维标度的定位方法2的辐射源位置估计均方根误差同样可以达到克拉美罗界(见图4.11和图4.13),这验证了4.3.4节理论性能分析的有效性;(2)随着辐射源与传感器距离的增加,其定位精度会逐渐降低(见图4.13和图4.14),其对近场源的定位精度要高于对远场源的定位精度(见图4.11和图4.12);(3)两类定位成功概率的理论值和仿真值相互吻合,并且在相同条件下第2类定位成功概率高于第1类定位成功概率(见图4.12和图4.14),这验证了3.2节理论性能分析的有效性。
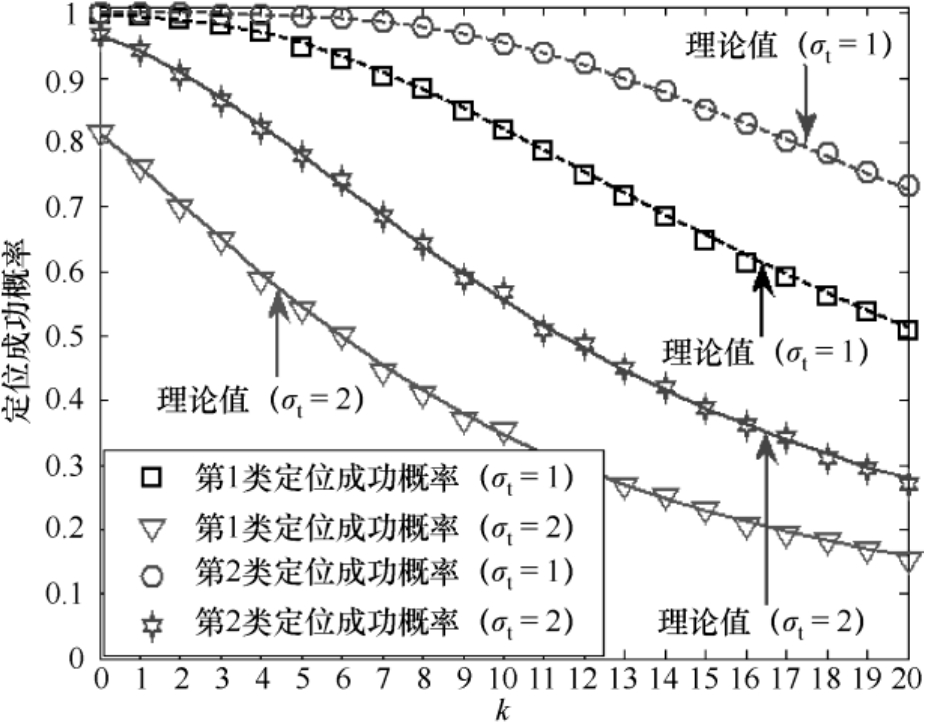
图4.14 辐射源定位成功概率随着参数 k 的变化曲线
[1] 参数 k 越大,辐射源与传感器之间的距离越远。