




在多维标度分析中,需要构造标量积矩阵。首先利用传感器和辐射源的位置向量定义如下坐标矩阵:
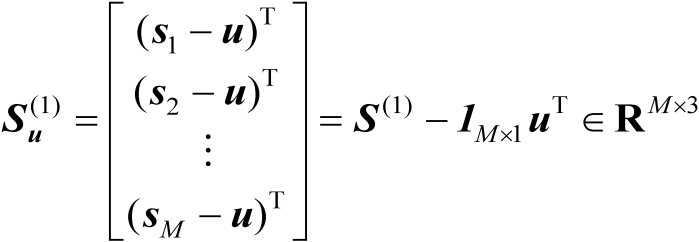
(4.5)
式中,
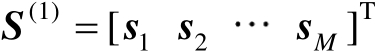
 。假设
。假设
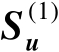 为列满秩矩阵,即有
为列满秩矩阵,即有
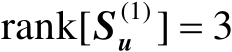 。然后构造如下标量积矩阵:
。然后构造如下标量积矩阵:
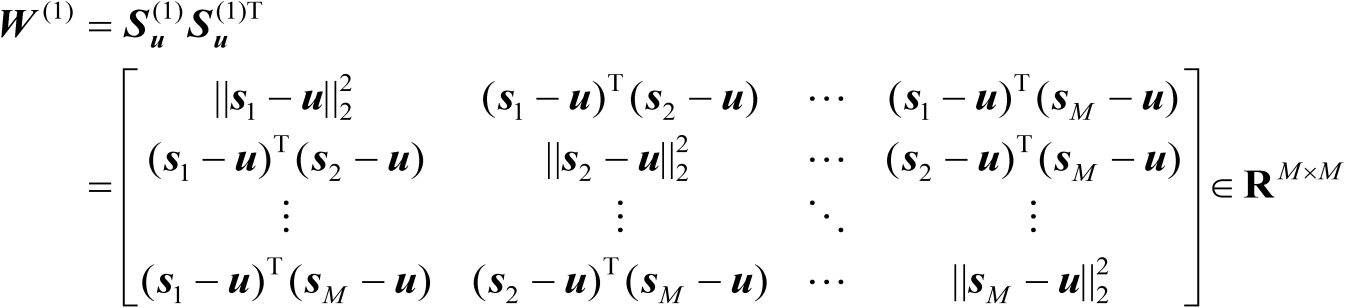
(4.6)
容易验证,该矩阵中的第
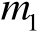 行、第
行、第
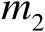 列元素为
列元素为
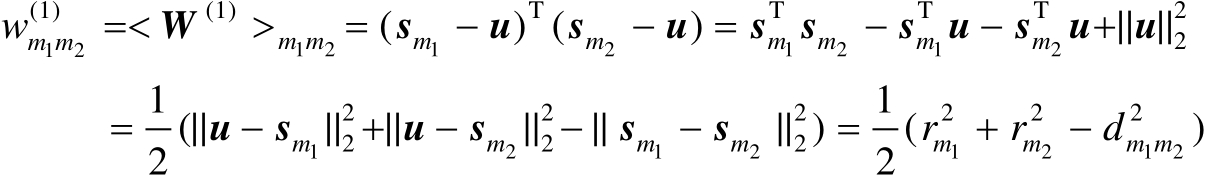
(4.7)
式中,
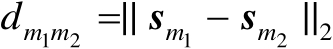 。式(4.7)实际上提供了构造矩阵
。式(4.7)实际上提供了构造矩阵
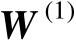 的计算公式,如下式所示:
的计算公式,如下式所示:
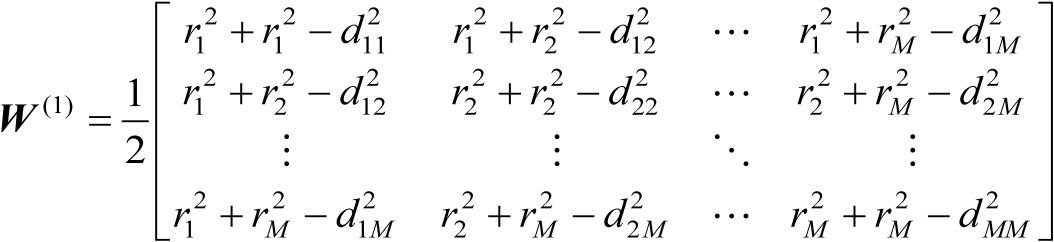
(4.8)
现对矩阵
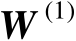 进行特征值分解,可得
进行特征值分解,可得
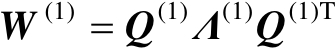
(4.9)
式中,
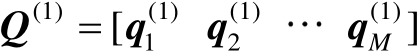 为特征向量构成的矩阵;
为特征向量构成的矩阵;
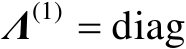
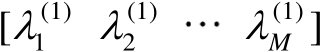 为特征值构成的对角矩阵,并且假设
为特征值构成的对角矩阵,并且假设
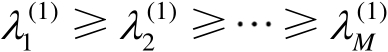 。由于
。由于
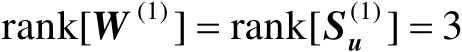 ,则有
,则有
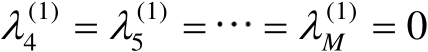 。若令
。若令
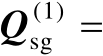
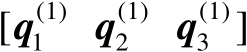 、
、
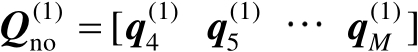 及
及
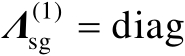
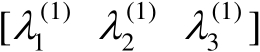 ,则可以将矩阵
,则可以将矩阵
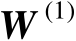 表示为
表示为
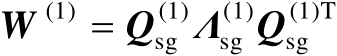
(4.10)
再利用特征向量之间的正交性可得
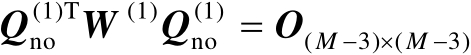
(4.11)
【注记4.1】
本章将矩阵
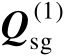 的列空间称为信号子空间(
的列空间称为信号子空间(
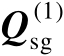 也称为信号子空间矩阵),将矩阵
也称为信号子空间矩阵),将矩阵
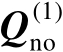 的列空间称为噪声子空间(
的列空间称为噪声子空间(
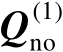 也称为噪声子空间矩阵)。
也称为噪声子空间矩阵)。
下面将给出一个重要的关系式,它对于确定辐射源位置至关重要。首先将式(4.6)代入式(4.11)中可得
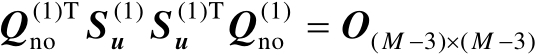
(4.12)
由式(4.12)可知
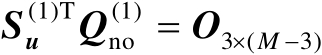
(4.13)
接着将式(4.5)代入式(4.13)中可得
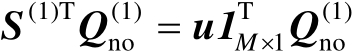
(4.14)
式(4.14)是关于辐射源位置向量
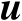 的子空间等式,但其中仅包含噪声子空间矩阵
的子空间等式,但其中仅包含噪声子空间矩阵
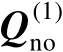 。根据式(4.10)可知,标量积矩阵
。根据式(4.10)可知,标量积矩阵
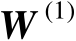 是由信号子空间矩阵
是由信号子空间矩阵
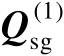 表示的,因此下面还需要获得向量
表示的,因此下面还需要获得向量
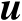 与矩阵
与矩阵
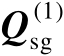 之间的关系式,具体可见如下命题
[28]
。
之间的关系式,具体可见如下命题
[28]
。
【命题4.1】
假设
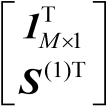 是行满秩矩阵,则有
是行满秩矩阵,则有
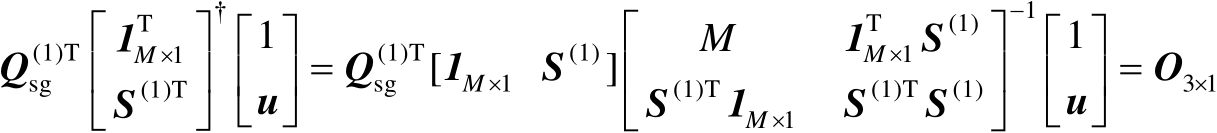
(4.15)
【证明】 首先利用式(4.14)可得
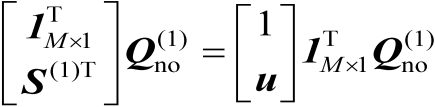
(4.16)
将式(4.16)两边右乘以
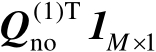 ,然后两边再同时除以
,然后两边再同时除以
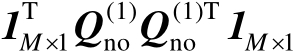 可得
可得
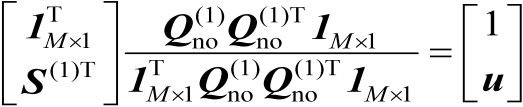
(4.17)
由于
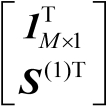 是行满秩矩阵,结合第2章命题2.5和式(4.17)可得
是行满秩矩阵,结合第2章命题2.5和式(4.17)可得
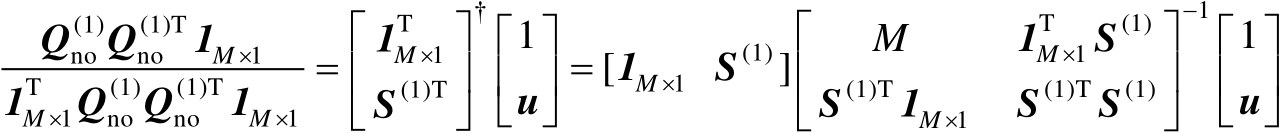
(4.18)
根据对称矩阵特征向量之间的正交性可知
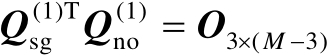 ,最后将该式与式(4.18)相结合可得
,最后将该式与式(4.18)相结合可得
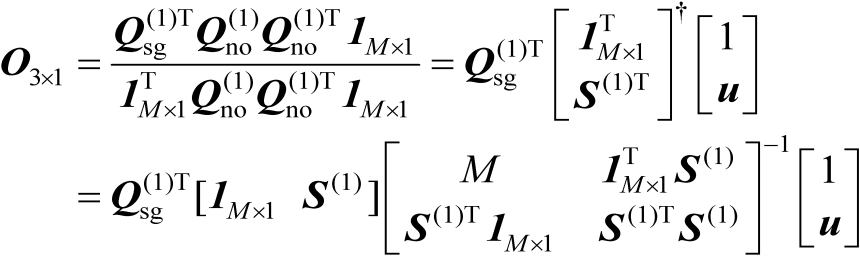
(4.19)
证毕。
式(4.15)给出的关系式至关重要,命题4.1是根据子空间正交性原理对其进行证明的,附录A.1中还基于矩阵求逆定理给出了另一种证明方法。
需要指出的是,式(4.15)并不是最终的关系式,为了得到用于定位的关系式,还需要将式(4.15)两边左乘以
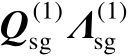 ,可得
,可得
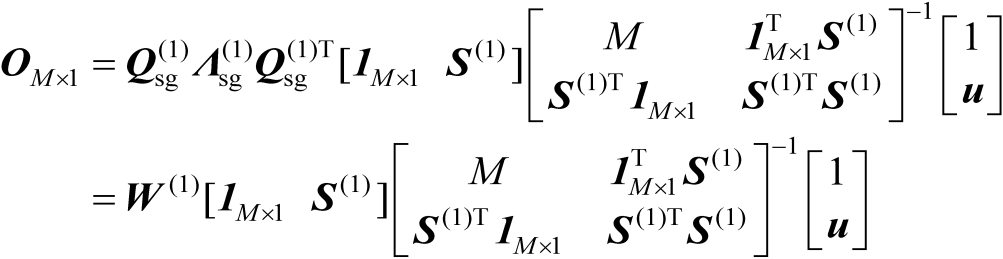
(4.20)
式中,第2个等号处的运算利用了式(4.10)。式(4.20)即为最终确定的关系式,它建立了关于辐射源位置向量
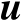 的伪线性等式,其中一共包含
的伪线性等式,其中一共包含
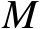 个等式,而TOA观测量也为
个等式,而TOA观测量也为
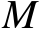 个,因此观测信息并无损失。
个,因此观测信息并无损失。
【注记4.2】
虽然在上面的推导过程中利用了信号子空间矩阵
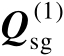 和噪声子空间矩阵
和噪声子空间矩阵
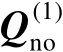 ,但是在最终得到的关系式(4.20)中并未出现这两个矩阵,这意味着无须进行矩阵特征值分解即可完成辐射源定位。
,但是在最终得到的关系式(4.20)中并未出现这两个矩阵,这意味着无须进行矩阵特征值分解即可完成辐射源定位。
下面将基于式(4.20)构建确定辐射源位置向量
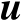 的估计准则,并且推导其最优解。为了简化数学表述,首先定义如下矩阵和向量:
的估计准则,并且推导其最优解。为了简化数学表述,首先定义如下矩阵和向量:
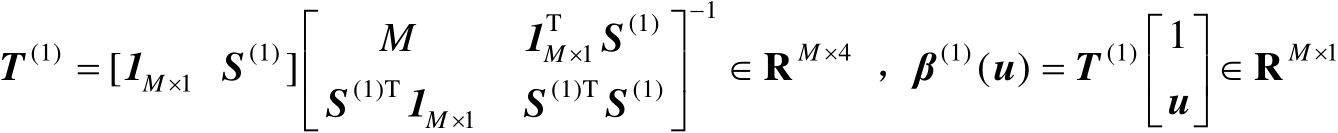
(4.21)
结合式(4.20)和式(4.21)可得
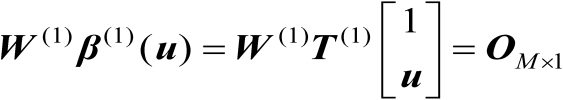
(4.22)
1.一阶误差扰动分析
在实际定位过程中,标量积矩阵
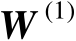 的真实值是未知的,因为其中的真实距离
的真实值是未知的,因为其中的真实距离
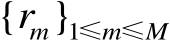 仅能用其观测值
仅能用其观测值
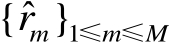 来代替,这必然会引入观测误差。不妨将含有观测误差的标量积矩阵
来代替,这必然会引入观测误差。不妨将含有观测误差的标量积矩阵
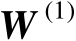 记为
记为
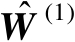 ,于是根据式(4.7)可知,矩阵
,于是根据式(4.7)可知,矩阵
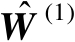 中的第
中的第
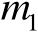 行、第
行、第
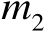 列元素为
列元素为
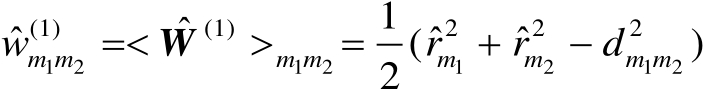
(4.23)
进一步可得
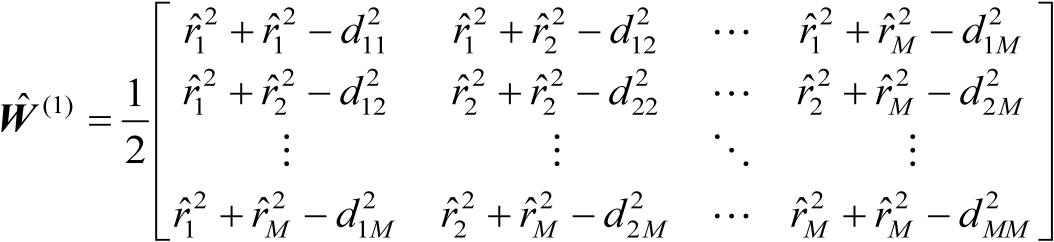
(4.24)
由于
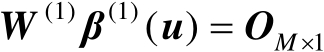 ,于是可以定义如下误差向量:
,于是可以定义如下误差向量:
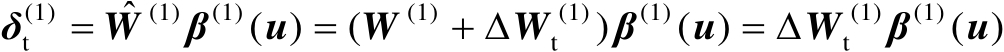
(4.25)
式中,
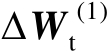 表示
表示
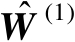 中的误差矩阵,即有
中的误差矩阵,即有
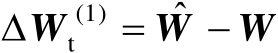 。若忽略观测误差
。若忽略观测误差
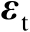 的二阶及其以上各阶项,则根据式(4.24)可以将误差矩阵
的二阶及其以上各阶项,则根据式(4.24)可以将误差矩阵
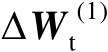 近似表示为
近似表示为
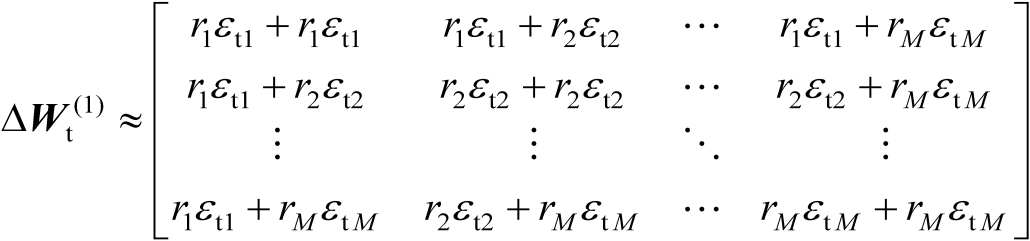
(4.26)
将式(4.26)代入式(4.25)中可以将误差向量
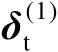 近似表示为关于观测误差
近似表示为关于观测误差
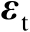 的线性函数,如下式所示:
的线性函数,如下式所示:
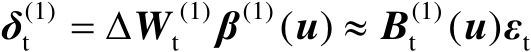
(4.27)
式中
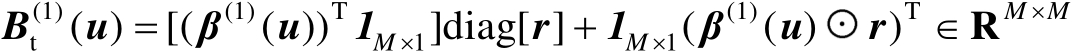
(4.28)
式(4.27)的推导见附录A.2。由式(4.27)可知,误差向量
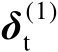 渐近服从零均值的高斯分布,并且其协方差矩阵为
渐近服从零均值的高斯分布,并且其协方差矩阵为
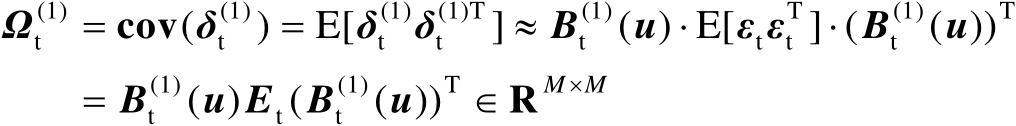
(4.29)
2.定位优化模型及其求解方法
基于式(4.25)和式(4.29)可以构建估计辐射源位置向量
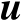 的优化准则,如下式所示:
的优化准则,如下式所示:
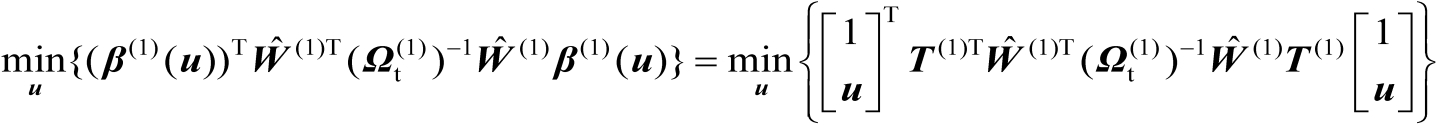
(4.30)
式中,
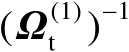 可以看作加权矩阵,其作用在于抑制观测误差
可以看作加权矩阵,其作用在于抑制观测误差
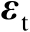 的影响。不妨将矩阵
的影响。不妨将矩阵
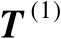 分块表示为
分块表示为
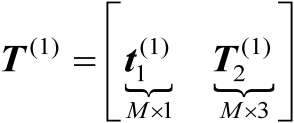
(4.31)
于是可以将式(4.30)重新写为
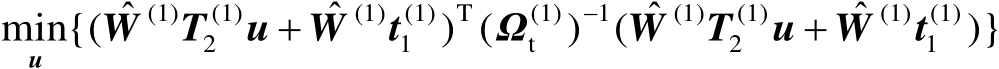
(4.32)
根据命题2.13可知,式(4.32)的最优解为

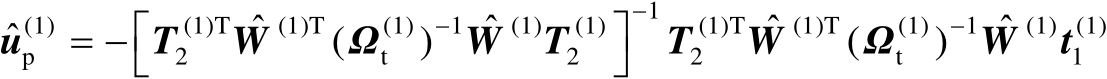
(4.33)
【注记4.3】
由式(4.29)可知,加权矩阵
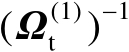 与辐射源位置向量
与辐射源位置向量
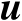 有关,因此严格来说,式(4.32)中的目标函数并不是关于向量
有关,因此严格来说,式(4.32)中的目标函数并不是关于向量
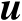 的二次函数。庆幸的是,该问题并不难以解决,可以先将
的二次函数。庆幸的是,该问题并不难以解决,可以先将
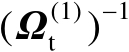 设为单位矩阵,从而获得关于向量
设为单位矩阵,从而获得关于向量
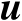 的初始值,然后再重新计算加权矩阵
的初始值,然后再重新计算加权矩阵
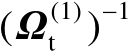 ,并再次得到向量
,并再次得到向量
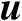 的估计值,重复此过程3~5次即可获得预期的估计精度。理论分析表明,在一阶误差分析理论框架下,加权矩阵
的估计值,重复此过程3~5次即可获得预期的估计精度。理论分析表明,在一阶误差分析理论框架下,加权矩阵
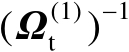 中的扰动误差并不会实质影响估计值
中的扰动误差并不会实质影响估计值
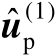 的统计性能。
的统计性能。
图4.1给出了本章第1种加权多维标度定位方法的流程图。

图4.1 本章第1种加权多维标度定位方法的流程图
下面将推导估计值
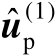 的理论性能,主要是推导估计均方误差矩阵,并将其与相应的克拉美罗界进行比较,从而证明其渐近最优性。这里采用的性能分析方法是一阶误差分析方法,即忽略观测误差
的理论性能,主要是推导估计均方误差矩阵,并将其与相应的克拉美罗界进行比较,从而证明其渐近最优性。这里采用的性能分析方法是一阶误差分析方法,即忽略观测误差
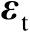 的二阶及其以上各阶项。
的二阶及其以上各阶项。
首先将最优解
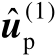 中的估计误差记为
中的估计误差记为
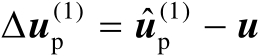 。基于式(4.33)和注记4.3中的讨论可知
。基于式(4.33)和注记4.3中的讨论可知
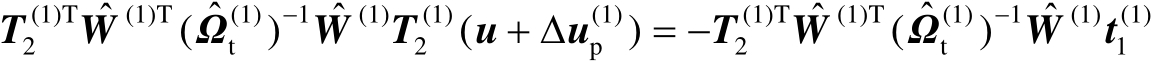
(4.34)
式中,
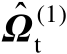 表示
表示
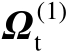 的估计值。在一阶误差分析框架下,基于式(4.34)可以进一步推得
的估计值。在一阶误差分析框架下,基于式(4.34)可以进一步推得
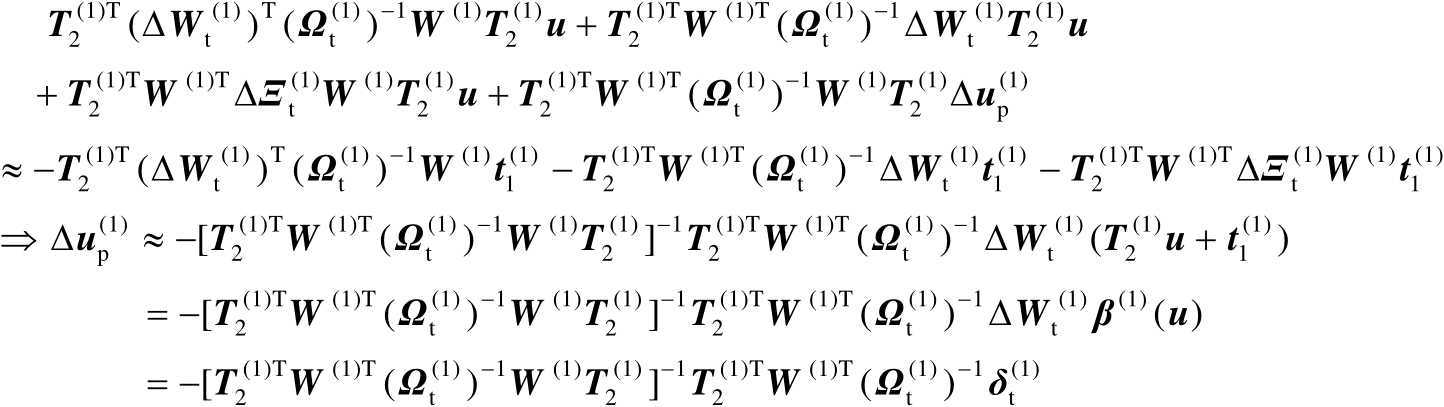
(4.35)
式中,
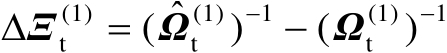 表示矩阵
表示矩阵
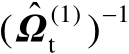 中的扰动误差。由式(4.35)可知,估计误差
中的扰动误差。由式(4.35)可知,估计误差
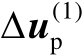 渐近服从零均值的高斯分布,因此估计值
渐近服从零均值的高斯分布,因此估计值
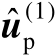 是渐近无偏估计,并且其均方误差矩阵为
是渐近无偏估计,并且其均方误差矩阵为
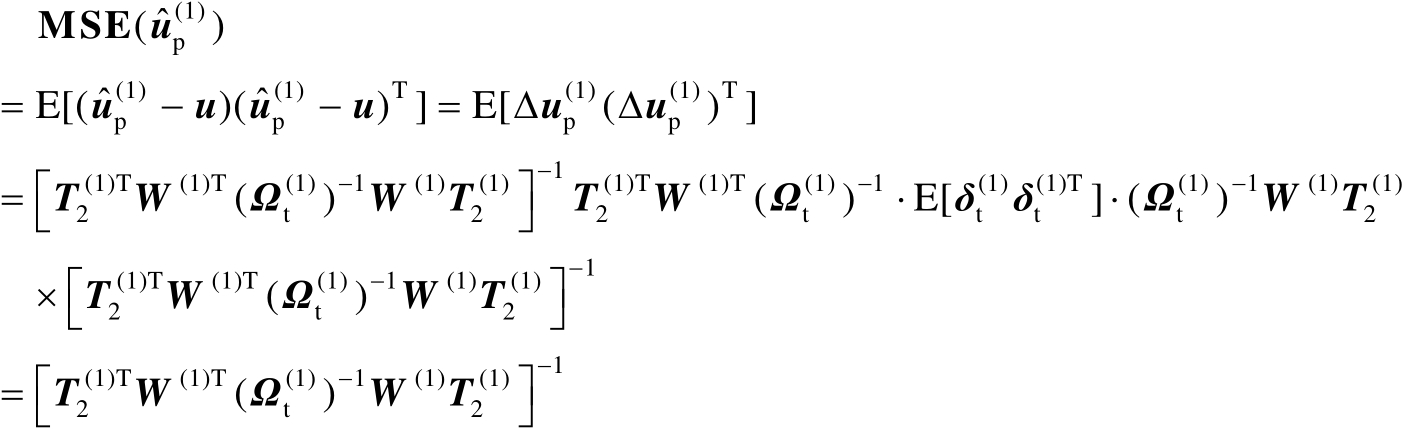
(4.36)
【注记4.4】
式(4.35)表明,在一阶误差分析理论框架下,矩阵
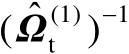 中的扰动误差
中的扰动误差
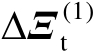 并不会实质影响估计值
并不会实质影响估计值
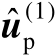 的统计性能。
的统计性能。
下面证明估计值
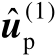 具有渐近最优性,也就是证明其估计均方误差矩阵可以渐近逼近相应的克拉美罗界,具体可见如下命题。
具有渐近最优性,也就是证明其估计均方误差矩阵可以渐近逼近相应的克拉美罗界,具体可见如下命题。
【命题4.2】
在一阶误差分析理论框架下,
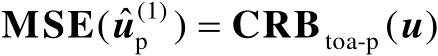
 。
。
【证明】 首先根据命题3.1可知
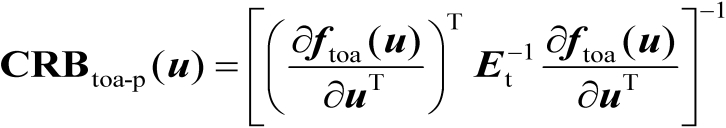
(4.37)
式中
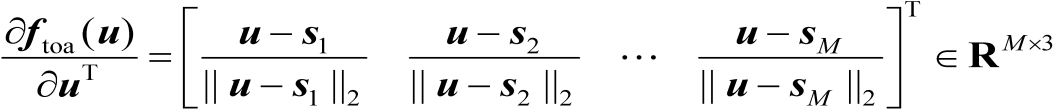
(4.38)
然后将式(4.29)代入式(4.36)中可得
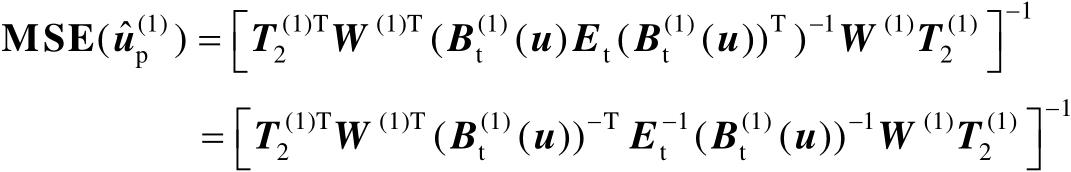
(4.39)
对比式(4.37)和式(4.39)可知,下面仅需要证明
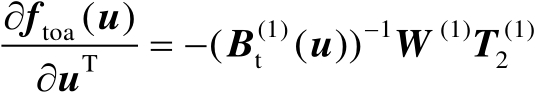
(4.40)
考虑等式
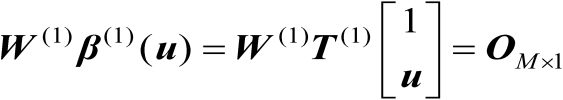 ,将该等式两边对向量
,将该等式两边对向量
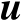 求导可得
求导可得
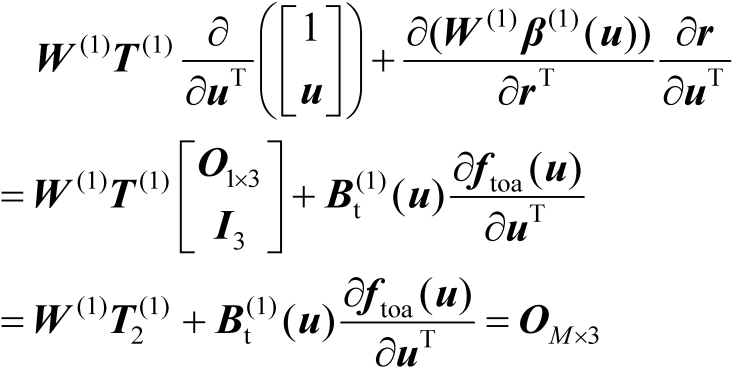
(4.41)
由式(4.41)可知式(4.40)成立。证毕。
假设利用5个传感器获得的TOA信息(也即距离信息)对辐射源进行定位,传感器三维位置坐标如表4.1所示,距离观测误差
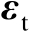 服从均值为零、协方差矩阵为
服从均值为零、协方差矩阵为
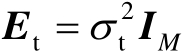 的高斯分布。
的高斯分布。
表4.1 传感器三维位置坐标 (单位:m)

首先将辐射源位置向量设为
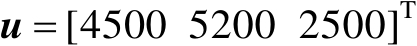 (m),将标准差设为
(m),将标准差设为
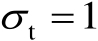 ,图4.2给出了定位结果散布图与定位误差椭圆曲线;图4.3给出了定位结果散布图与误差概率圆环曲线。
,图4.2给出了定位结果散布图与定位误差椭圆曲线;图4.3给出了定位结果散布图与误差概率圆环曲线。
图4.2 定位结果散布图与定位误差椭圆曲线
图4.3 定位结果散布图与误差概率圆环曲线
然后将辐射源坐标设为两种情形:第1种是近场源,其位置向量为
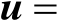
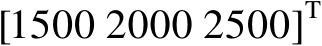 (m);第2种是远场源,其位置向量为
(m);第2种是远场源,其位置向量为
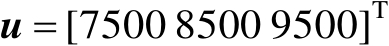 (m)。改变标准差
(m)。改变标准差
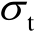 的数值,图4.4给出了辐射源位置估计均方根误差随着标准差
的数值,图4.4给出了辐射源位置估计均方根误差随着标准差
 的变化曲线;图4.5给出了辐射源定位成功概率随着标准差
的变化曲线;图4.5给出了辐射源定位成功概率随着标准差
 的变化曲线(图中的理论值是根据式(3.29)和式(3.36)计算得出的,其中
的变化曲线(图中的理论值是根据式(3.29)和式(3.36)计算得出的,其中
 m)。
m)。
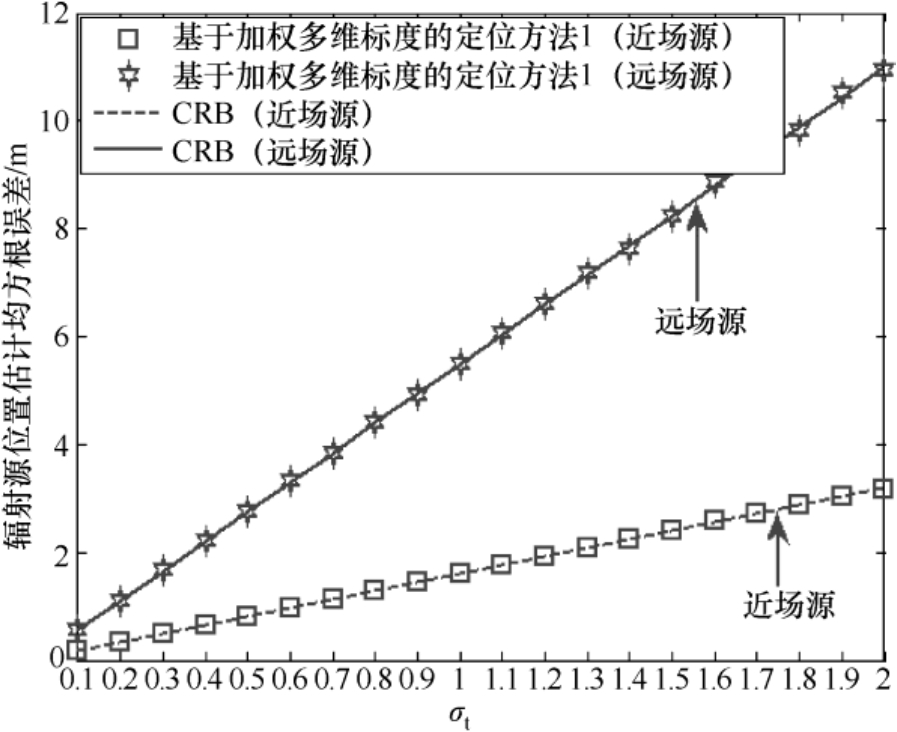
图4.4 辐射源位置估计均方根误差随着标准差 σ t 的变化曲线
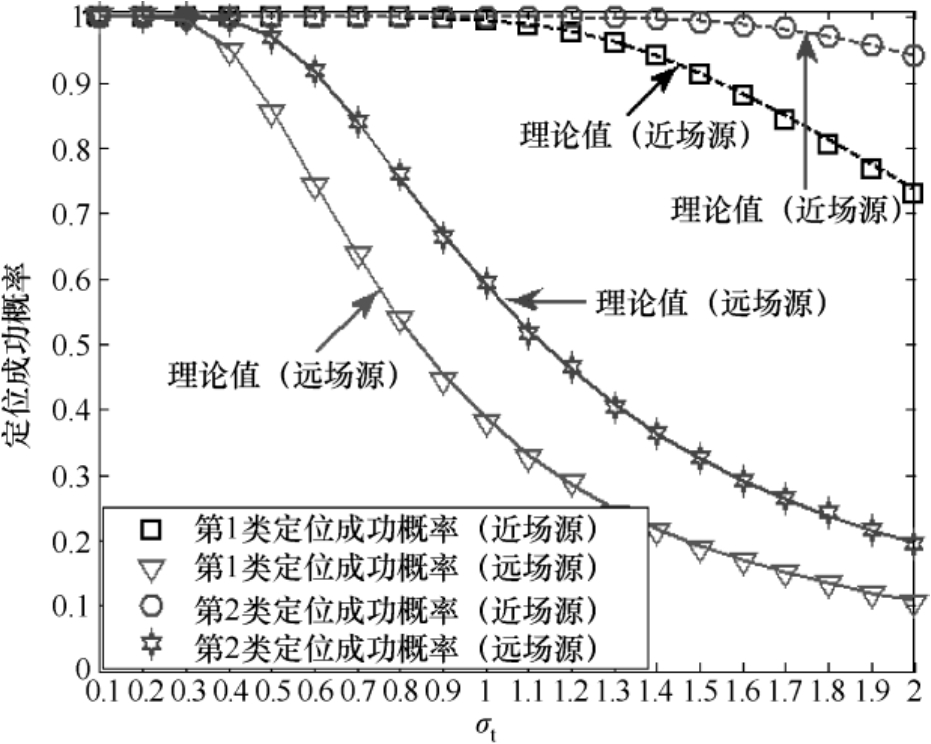
图4.5 辐射源定位成功概率随着标准差 σ t 的变化曲线
最后将标准差
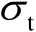 设为两种情形:第1种是
设为两种情形:第1种是
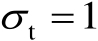 ;第2种是
;第2种是
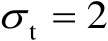 ,将辐射源位置向量设为
,将辐射源位置向量设为
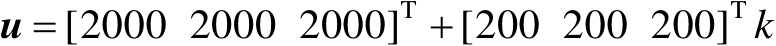 (m)
[1]
。改变参数
(m)
[1]
。改变参数
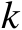 的数值,图4.6给出了辐射源位置估计均方根误差随着参数
的数值,图4.6给出了辐射源位置估计均方根误差随着参数
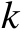 的变化曲线;图4.7给出了辐射源定位成功概率随着参数
的变化曲线;图4.7给出了辐射源定位成功概率随着参数
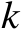 的变化曲线(图中的理论值是根据式(3.29)和式(3.36)计算得出的,其中
的变化曲线(图中的理论值是根据式(3.29)和式(3.36)计算得出的,其中
 m)。
m)。
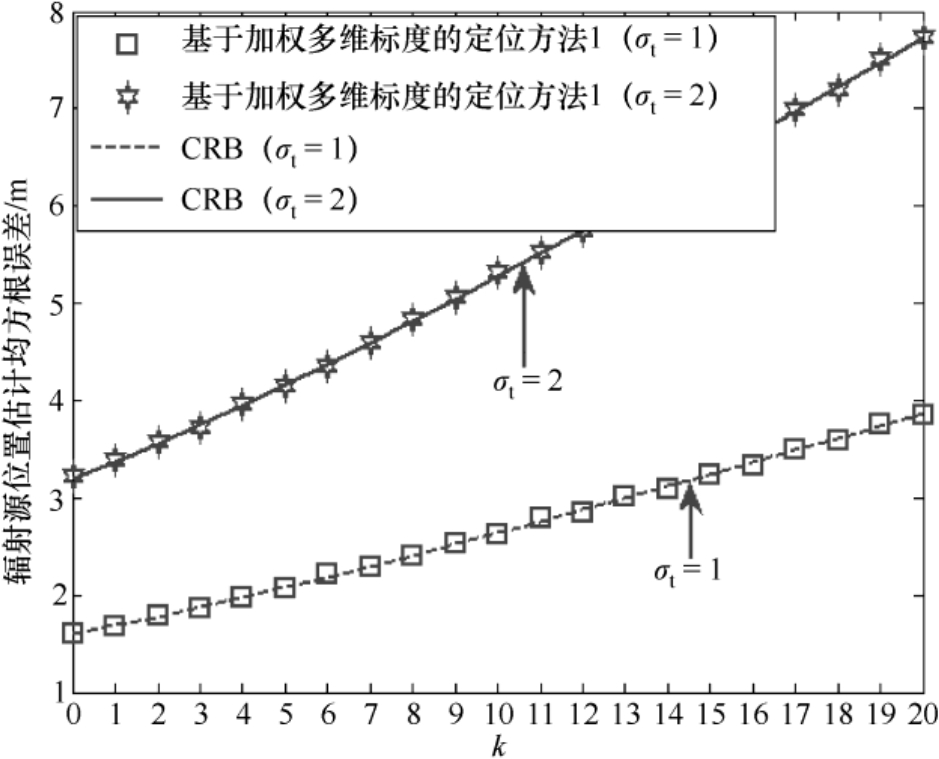
图4.6 辐射源位置估计均方根误差随着参数 k 的变化曲线
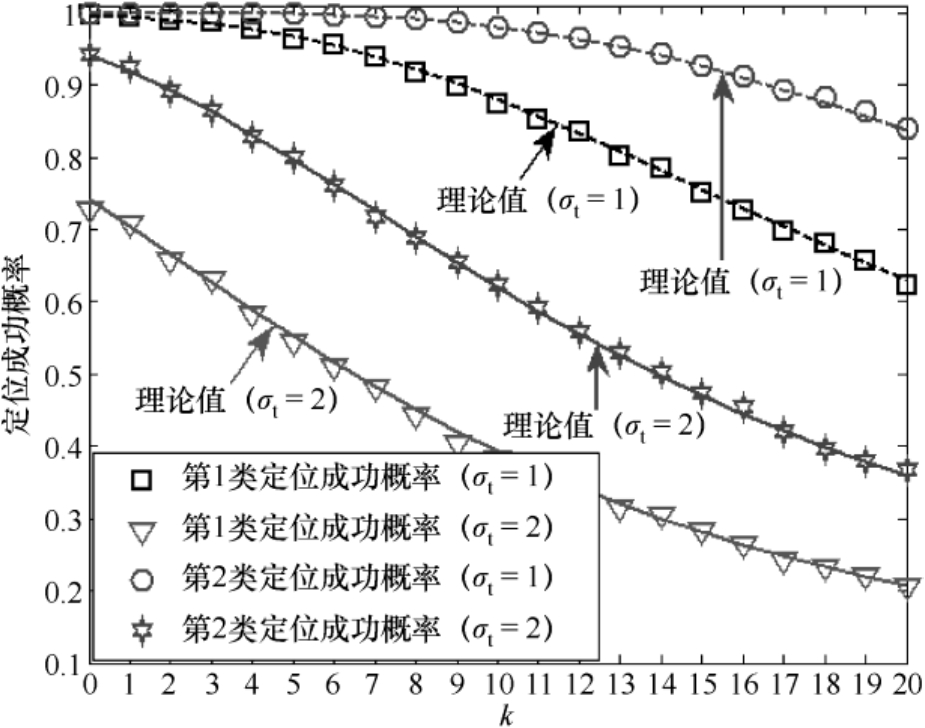
图4.7 辐射源定位成功概率随着参数 k 的变化曲线
从图4.4~图4.7可以看出:(1)基于加权多维标度定位方法1的辐射源位置估计均方根误差可以达到克拉美罗界(见图4.4和图4.6),这验证了4.2.4节理论性能分析的有效性;(2)随着辐射源与传感器距离的增加,其定位精度会逐渐降低(见图4.6和图4.7),其对近场源的定位精度要高于对远场源的定位精度(见图4.4和图4.5);(3)两类定位成功概率的理论值和仿真值相互吻合,并且在相同条件下第2类定位成功概率高于第1类定位成功概率(见图4.5和图4.7),这验证了3.2节理论性能分析的有效性。