




本节将介绍定位误差概率圆环(Circular Error Probable,CEP)的基本概念,这是一种相对粗糙但简单的刻画定位精度的度量标准。误差概率圆环定义了一个圆,其圆心位于估计值的均值(对于无偏估计而言就是辐射源的真实位置),圆半径的选取原则是保证估计值以概率0.5落入圆内。
为了简化数学分析,下面以
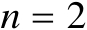 为例进行讨论。根据上述定义可知,若将误差概率圆环半径(CEP半径)记为
为例进行讨论。根据上述定义可知,若将误差概率圆环半径(CEP半径)记为
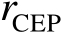 ,则有
,则有
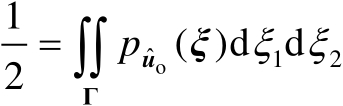
(3.62)
式中
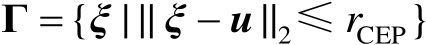
(3.63)
下面将基于式(3.62)推导半径
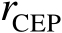 的表达式。
的表达式。
首先类似于式(3.47)可知
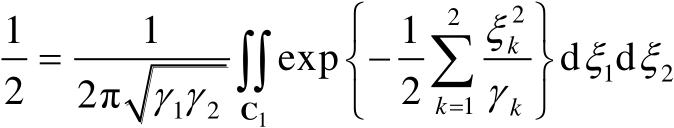
(3.64)
式中
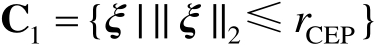
(3.65)
利用变量替换
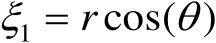 和
和
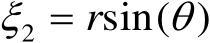 可以将式(3.64)转化为
可以将式(3.64)转化为
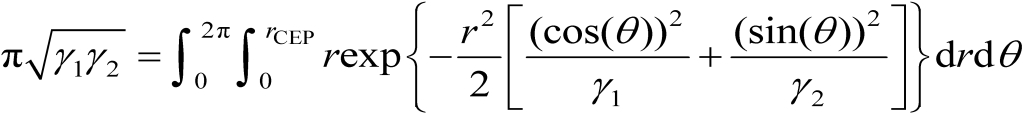
(3.66)
为了简化式(3.66),需要引入第1类零阶修正贝塞尔函数
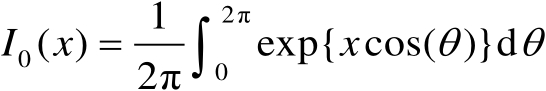
(3.67)
式中的积分具有周期性,对于任意正整数
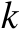 都满足
都满足
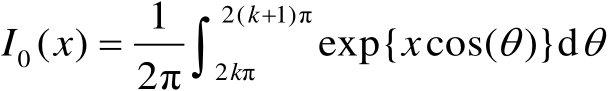
(3.68)
由式(3.68)可以推得
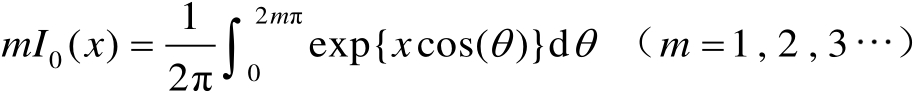
(3.69)
若令
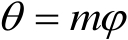 ,并进行坐标变换可得
,并进行坐标变换可得
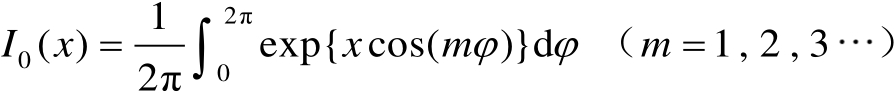
(3.70)
利用三角恒等式可得
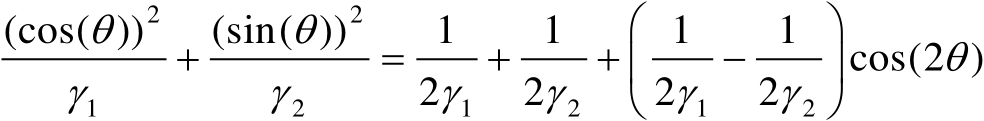
(3.71)
将式(3.71)代入式(3.66)中可得
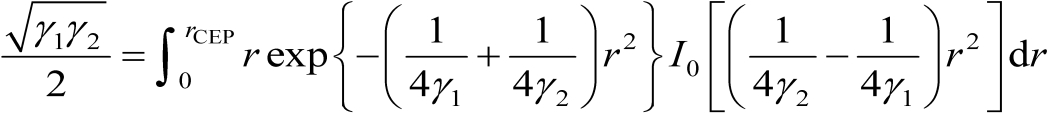
(3.72)
通过坐标变换可以最终得到等式
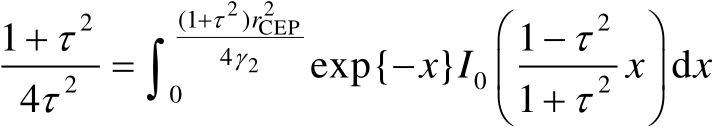
(3.73)
式中,
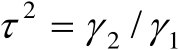 。
。
从式(3.73)中不难看出,半径
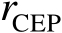 的表达式应为
的表达式应为
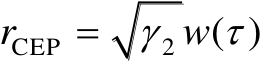 ,其中
,其中
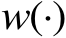 是某个确定但未知的函数。如果式(3.55)中的
是某个确定但未知的函数。如果式(3.55)中的
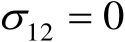 及
及
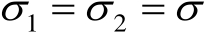 ,则有
,则有
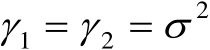 ,此时由式(3.73)可以解得
,此时由式(3.73)可以解得
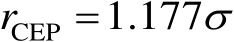 。然而,绝大多数情况下
。然而,绝大多数情况下
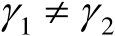 ,此时需要利用数值积分获得
,此时需要利用数值积分获得
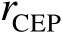 的数值解。值得一提的是,文献[60]中给出了计算
的数值解。值得一提的是,文献[60]中给出了计算
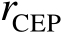 的简单公式,如下式所示:
的简单公式,如下式所示:
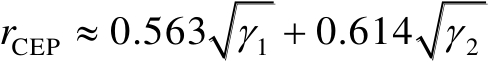
(3.74)
式(3.74)的误差取决于
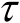 的数值。
的数值。
另一方面,利用式(3.30)还可以获得另一种计算
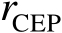 的方法。根据式(3.30)和式(3.36)可知
的方法。根据式(3.30)和式(3.36)可知
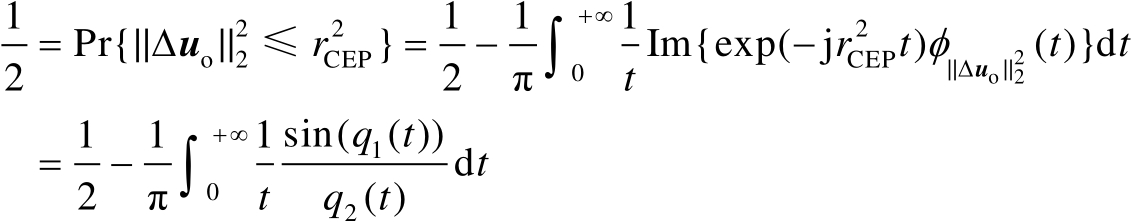
(3.75)
式中
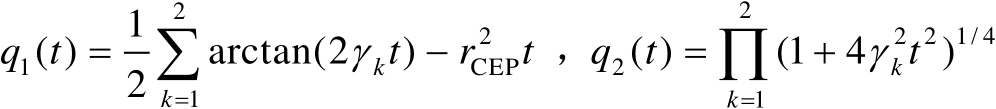
(3.76)
将式(3.76)代入式(3.75)中可得
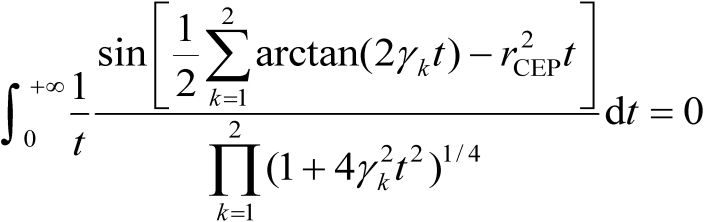
(3.77)
由式(3.77)可知,半径
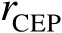 可以看作一维优化问题
可以看作一维优化问题
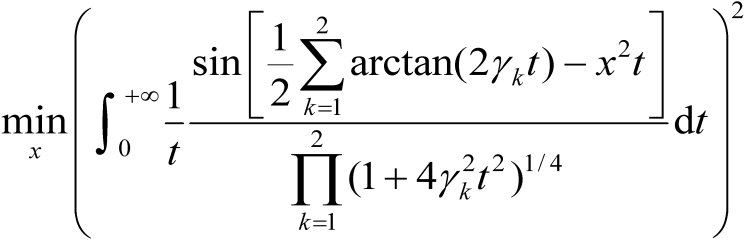
(3.78)
的最优解。通过优化求解式(3.78)即可获得半径
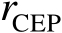 的数值解。
的数值解。
基于图3.2描述的定位场景,图3.6和图3.7分别给出了辐射源坐标(220m,90m)和(10m,30m)对应的误差概率圆环曲线,图中的两个圆环半径分别是基于式(3.74)和式(3.78)计算所得的。从图中不难看出,两种方法计算出的误差概率圆环半径是比较接近的。
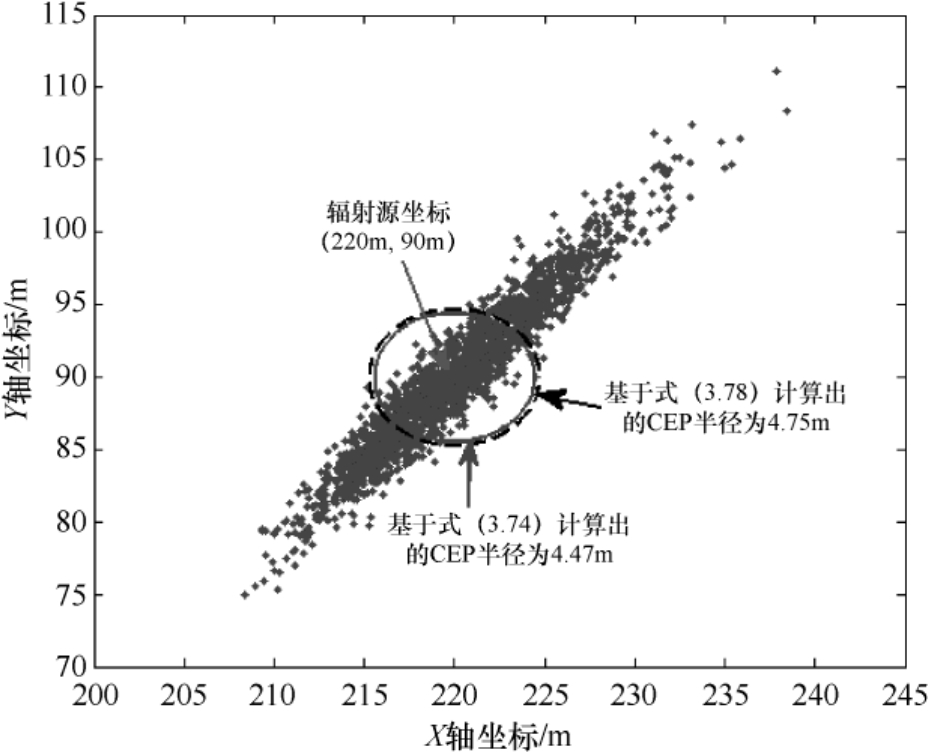
图3.6 时差定位结果散布图与误差概率圆环曲线(辐射源坐标为(220m,90m))
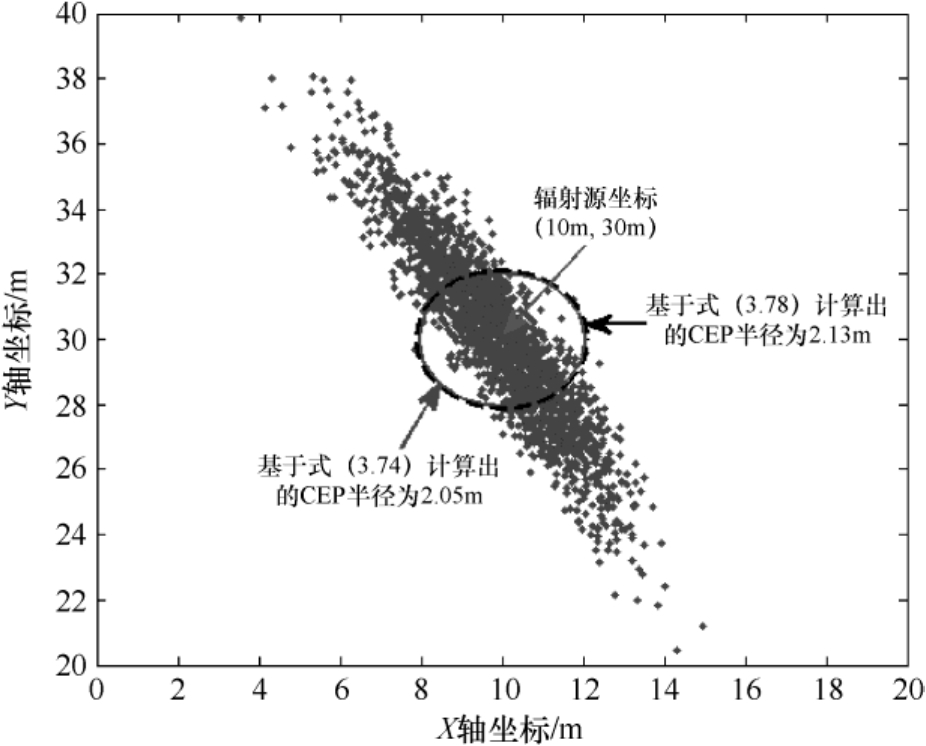
图3.7 时差定位结果散布图与误差概率圆环曲线(辐射源坐标为(10m,30m))
[1]
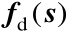 也应是校正源位置向量
也应是校正源位置向量
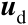 的函数,但由于
的函数,但由于
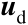 精确已知,所以无须将其作为变量来看待。
精确已知,所以无须将其作为变量来看待。