




本节将介绍定位误差椭圆的相关概念。假设辐射源位置向量
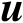 的某个无偏估计值为
的某个无偏估计值为
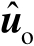 ,服从高斯分布,并且均方误差矩阵为
,服从高斯分布,并且均方误差矩阵为
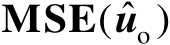 ,则估计向量
,则估计向量
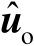 的概率密度函数为
的概率密度函数为
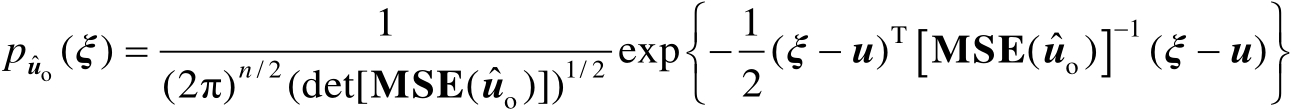
(3.40)
该概率密度函数的等值曲线可以表示为
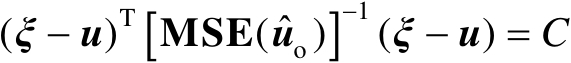
(3.41)
式中,
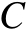 为任意正常数,由它可以确定曲线表面所包围的
为任意正常数,由它可以确定曲线表面所包围的
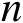 维区域大小。当
维区域大小。当
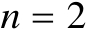 时,其表面为椭圆;当
时,其表面为椭圆;当
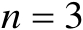 时,其表面为椭圆体;当
时,其表面为椭圆体;当
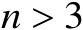 时,其表面为超椭圆体。需要指出的是,若
时,其表面为超椭圆体。需要指出的是,若
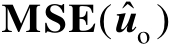 不为对角矩阵,则超椭圆体的主轴就不会与坐标轴平行。
不为对角矩阵,则超椭圆体的主轴就不会与坐标轴平行。
估计向量
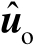 位于式(3.41)定义的超椭圆体内部的概率为
位于式(3.41)定义的超椭圆体内部的概率为
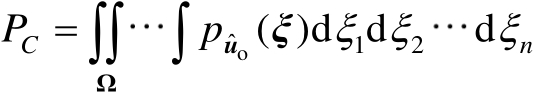
(3.42)
式中,积分区域
 为
为
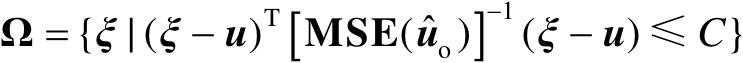
(3.43)
下面将式(3.42)中的多重积分转化为单重积分。
首先引入变量
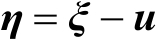 ,此时可以将式(3.42)转化为
,此时可以将式(3.42)转化为
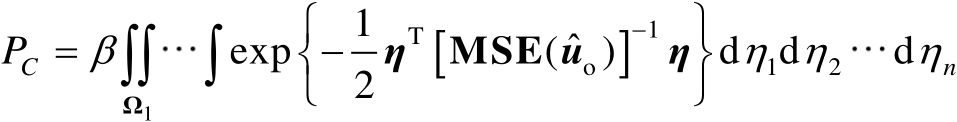
(3.44)
式中,
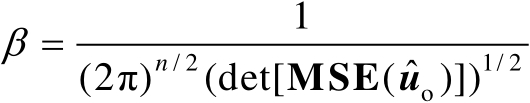 ,其中的积分区域
,其中的积分区域
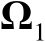 为
为
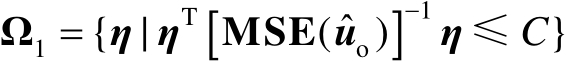
(3.45)
下面简化式(3.44),通过旋转坐标轴以使其与超椭圆体主轴平行。由于
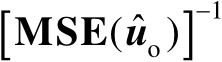 是对称正定矩阵,则一定存在正交矩阵
是对称正定矩阵,则一定存在正交矩阵
 满足
满足
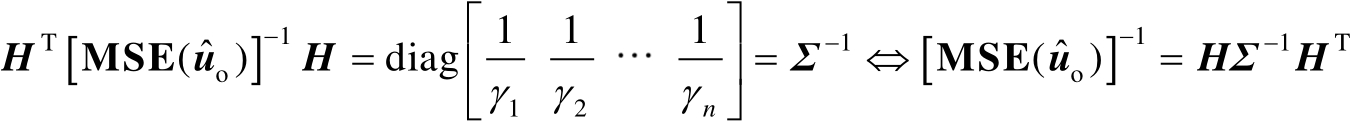
(3.46)
式中,
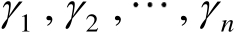 表示矩阵
表示矩阵
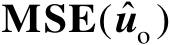 的
的
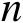 个特征值。若令
个特征值。若令
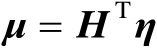 ,则可以将式(3.44)转化为
,则可以将式(3.44)转化为
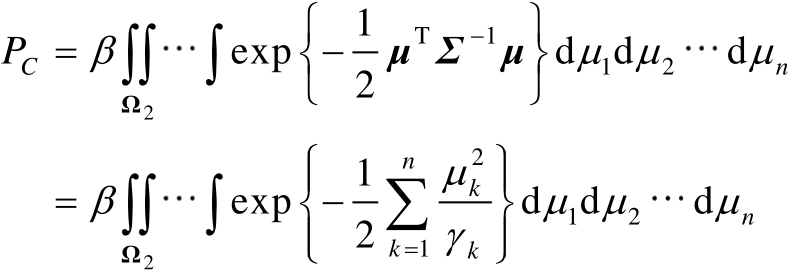
(3.47)
式中
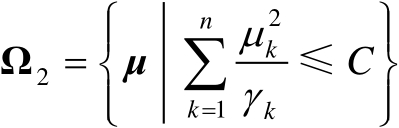
(3.48)
若再令
 ,则还可以将式(3.47)进一步简化为
,则还可以将式(3.47)进一步简化为
(3.49)
式中
(3.50)
式(3.49)中第2个等号处的运算利用了等式
 。根据文献[60]可知,对于半径为
。根据文献[60]可知,对于半径为
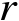 的超球体
的超球体
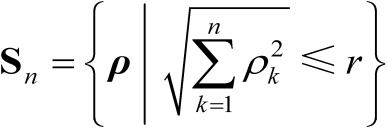 ,其体积为
,其体积为
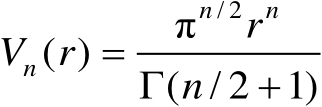
(3.51)
式中,
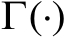 为伽马函数。由式(3.51)可知,超球体的体积微分与半径微分之间满足
为伽马函数。由式(3.51)可知,超球体的体积微分与半径微分之间满足
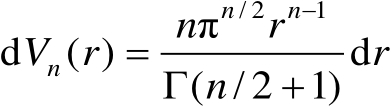
(3.52)
于是可以将式(3.49)最终简化为
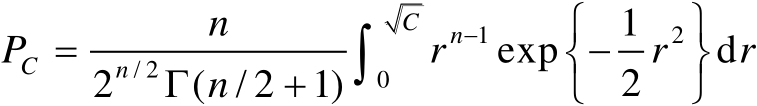
(3.53)
不难证明,当
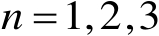 时,式(3.53)中的积分式可以分别表示为如下更为简化的形式:
时,式(3.53)中的积分式可以分别表示为如下更为简化的形式:
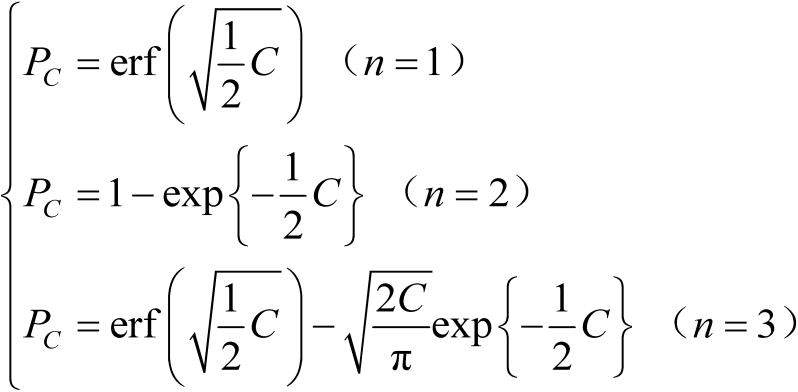
(3.54)
式中,
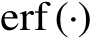 表示误差函数,其表达式为
表示误差函数,其表达式为
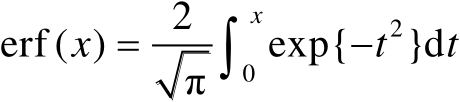 。
。
【注记3.11】
概率
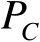 随着参数
随着参数
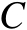 的增大而单调递增,如图3.1所示。
的增大而单调递增,如图3.1所示。
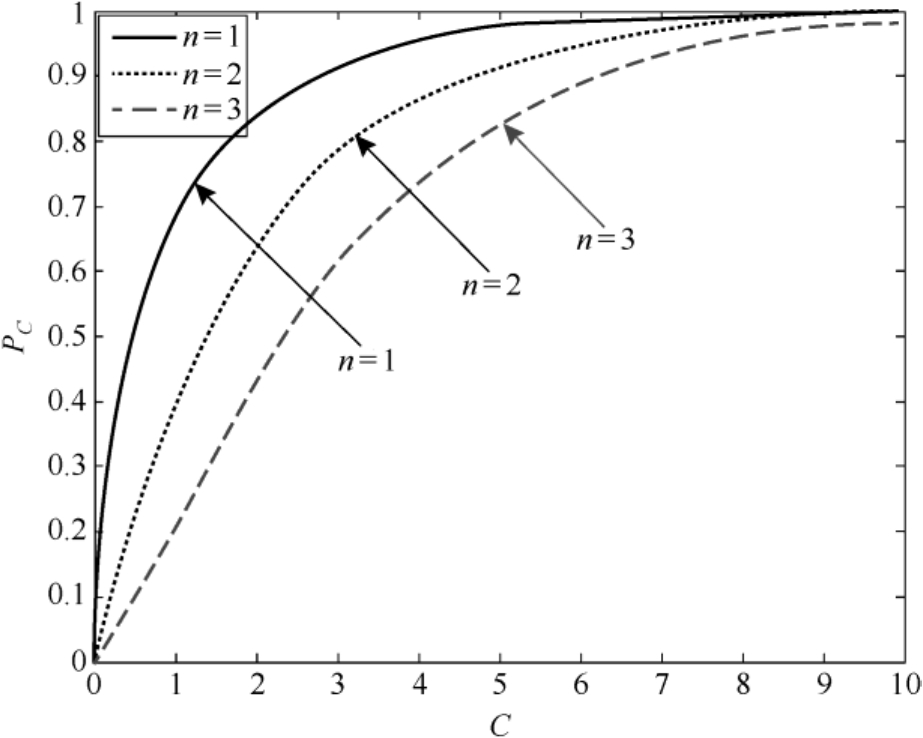
图3.1 概率
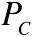 随着参数
随着参数
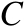 的变化曲线
的变化曲线
定位误差椭圆面积能够体现出定位精度的高低。下面将参数
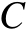 固定为
固定为
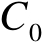 ,将概率
,将概率
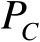 固定为
固定为
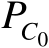 ,然后以
,然后以
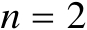 为例,推导定位误差椭圆
为例,推导定位误差椭圆
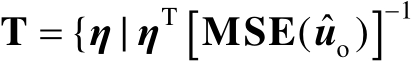
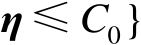 的面积。对于固定概率
的面积。对于固定概率
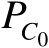 而言,定位误差椭圆面积越小,定位精度越高。
而言,定位误差椭圆面积越小,定位精度越高。
首先将二维均方误差矩阵
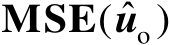 表示为
表示为
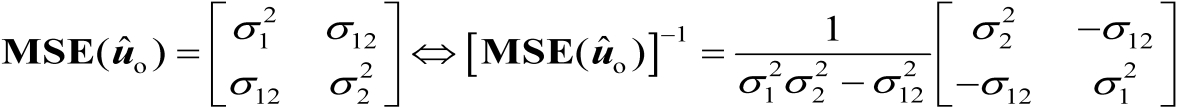
(3.55)
为了推导椭圆
 的面积,需要进行坐标轴旋转,以使得坐标轴方向与椭圆主轴方向一致。针对二维坐标系,其旋转矩阵可以表示为
的面积,需要进行坐标轴旋转,以使得坐标轴方向与椭圆主轴方向一致。针对二维坐标系,其旋转矩阵可以表示为
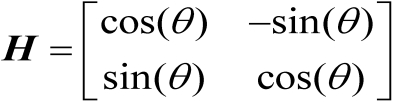
(3.56)
式中,旋转角度
 的选取应能使
的选取应能使
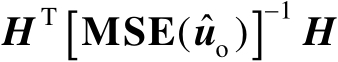 为对角矩阵。结合式(3.55)和式(3.56)可得
为对角矩阵。结合式(3.55)和式(3.56)可得
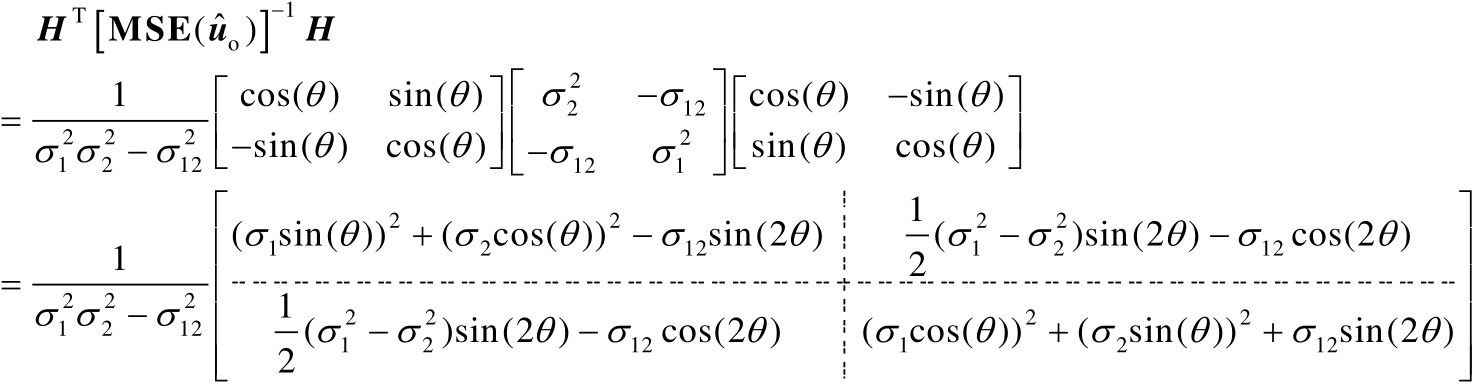
(3.57)
为了使
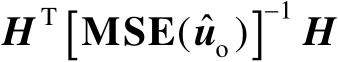 为对角矩阵,需要满足
为对角矩阵,需要满足
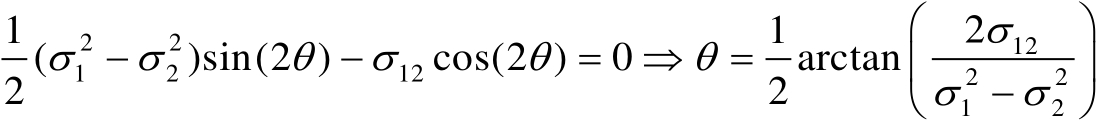
(3.58)
当
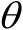 满足式(3.58)时,矩阵
满足式(3.58)时,矩阵
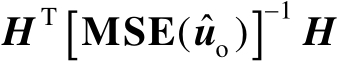 可以写为
可以写为
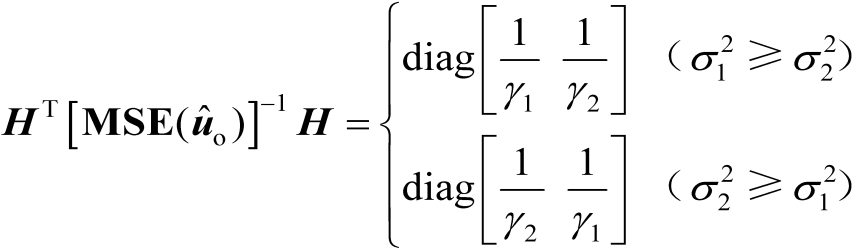
(3.59)
式中,
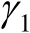 和
和
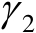 表示矩阵
表示矩阵
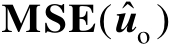 的两个特征值,并且满足
的两个特征值,并且满足
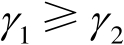 ,它们的表达式分别为
,它们的表达式分别为
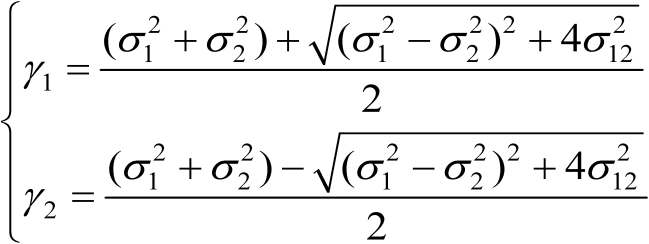
(3.60)
若令
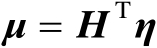 ,则旧坐标系中由
,则旧坐标系中由
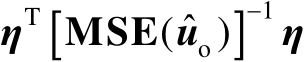 定义的椭圆在新坐标系中将由
定义的椭圆在新坐标系中将由
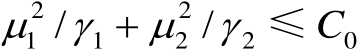 或
或
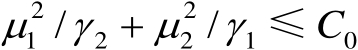 来描述,该椭圆的主轴和副轴的长度分别为
来描述,该椭圆的主轴和副轴的长度分别为
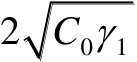 和
和
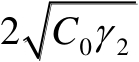 ,于是椭圆
,于是椭圆
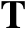 的面积为
的面积为
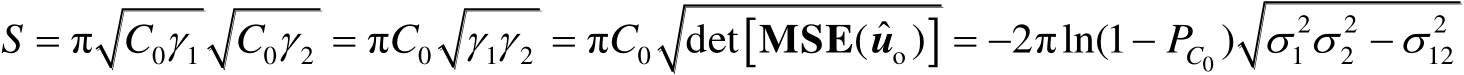
(3.61)
式中,第4个等号处的运算利用了关系式
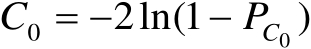 。
。
需要指出的是,定位误差椭圆面积和形状不仅与定位观测量的精度有关,还与辐射源与传感器之间的相对位置有关。图3.2给出了在5站时差定位场景下,辐射源处于不同位置时的定位结果散布图,其中给出了2000次蒙特卡洛独立实验的结果,定位方法采用文献[58]中的泰勒级数迭代法,距离差(可等价为时间差)观测误差的协方差矩阵设为
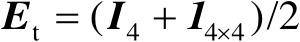 。从图中不难看出,定位结果散布图呈椭圆形分布,并且定位误差椭圆面积和形状与辐射源位置有关,椭圆面积越小,定位精度越高。图3.3给出了时差定位误差椭圆面积随着概率
。从图中不难看出,定位结果散布图呈椭圆形分布,并且定位误差椭圆面积和形状与辐射源位置有关,椭圆面积越小,定位精度越高。图3.3给出了时差定位误差椭圆面积随着概率
 的变化曲线,其中选取了4个不同的位置坐标。从图中可以看出,定位误差椭圆面积随着概率
的变化曲线,其中选取了4个不同的位置坐标。从图中可以看出,定位误差椭圆面积随着概率
 的增加而增大。图3.4和图3.5分别将辐射源坐标(220m,90m)和(10m,30m)对应的定位结果散布图进行了显示放大,图中还给出了3个概率值(分别为0.5、0.7及0.9)对应的定位误差椭圆曲线。
的增加而增大。图3.4和图3.5分别将辐射源坐标(220m,90m)和(10m,30m)对应的定位结果散布图进行了显示放大,图中还给出了3个概率值(分别为0.5、0.7及0.9)对应的定位误差椭圆曲线。
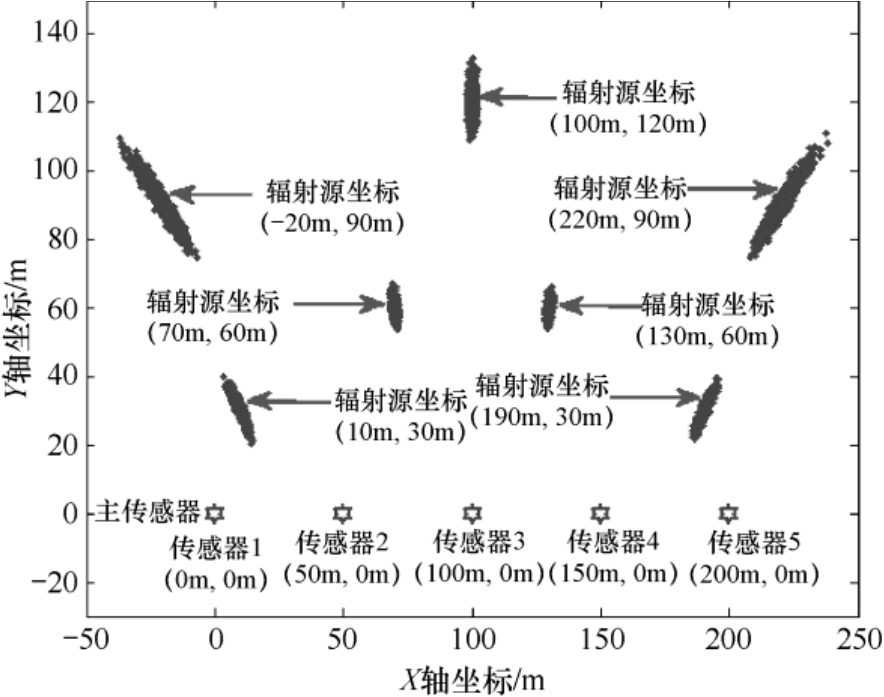
图3.2 传感器位置分布与时差定位结果散布图
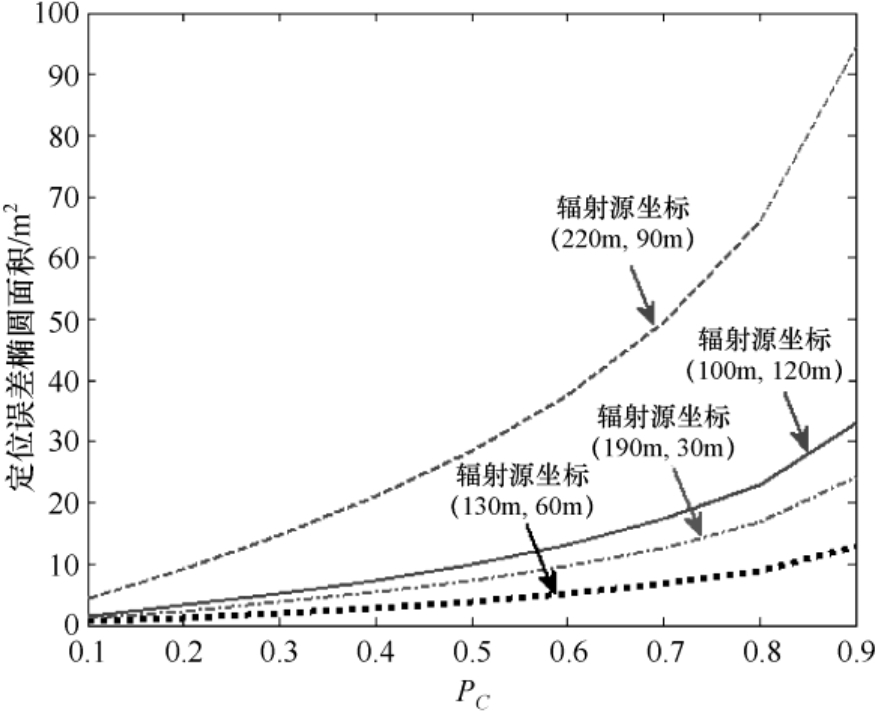
图3.3 时差定位误差椭圆面积随着概率 P C 的变化曲线
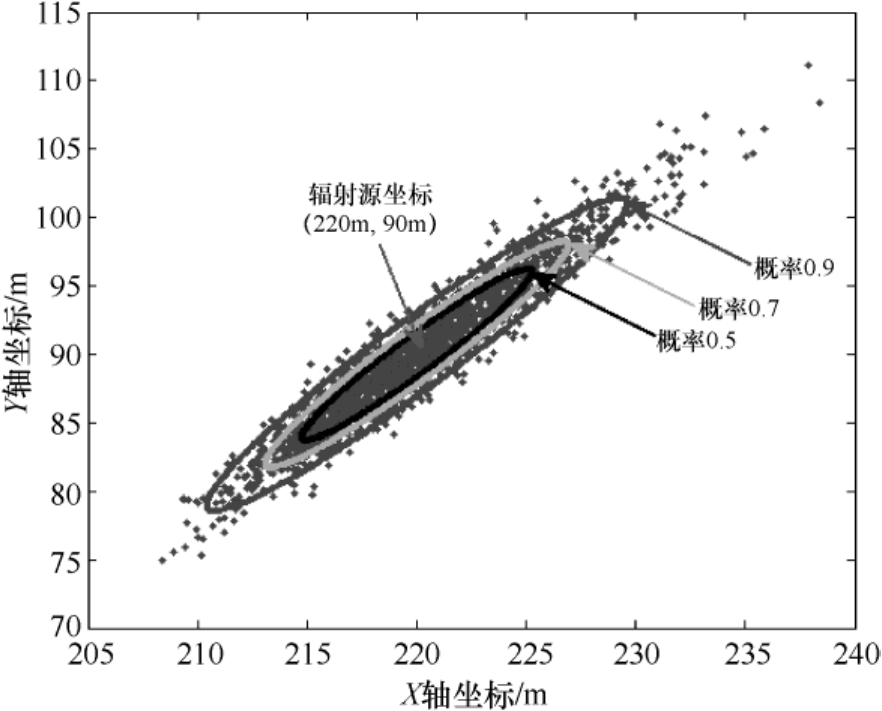
图3.4 时差定位结果散布图与误差椭圆曲线(辐射源坐标为(220m,90m))
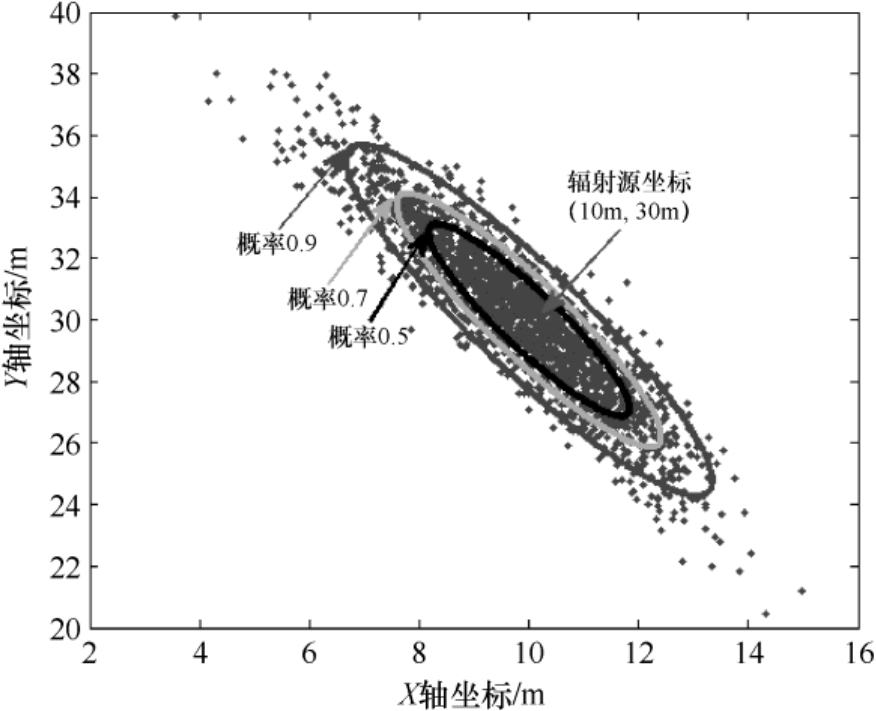
图3.5 时差定位结果散布图与误差椭圆曲线(辐射源坐标为(10m,30m))