




本节将给出定位成功概率的定义及其理论计算公式。假设辐射源位置向量
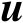 的某个无偏估计值为
的某个无偏估计值为
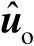 ,其均方误差矩阵为
,其均方误差矩阵为
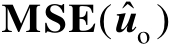 ,于是有
,于是有
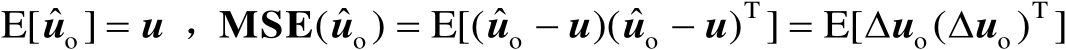
(3.27)
式中,
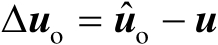 表示估计误差,假设其服从高斯分布,并且其均值为零,协方差矩阵为
表示估计误差,假设其服从高斯分布,并且其均值为零,协方差矩阵为
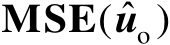 。
。
下面给出两类定位成功概率的定义,并且分别推导它们的理论表达式。
【定义3.1】
若定位误差满足
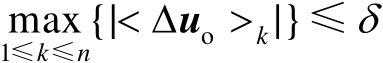 (其中
(其中
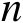 表示误差向量
表示误差向量
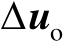 的维数),则认为是第1类定位成功。
的维数),则认为是第1类定位成功。
由于误差向量
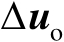 的概率密度函数为
的概率密度函数为
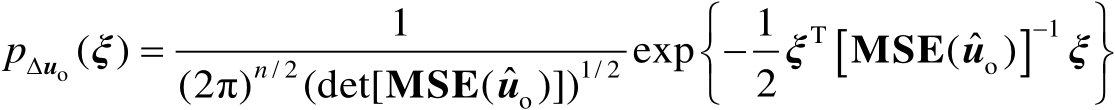
(3.28)
于是第1类定位成功概率的计算公式为
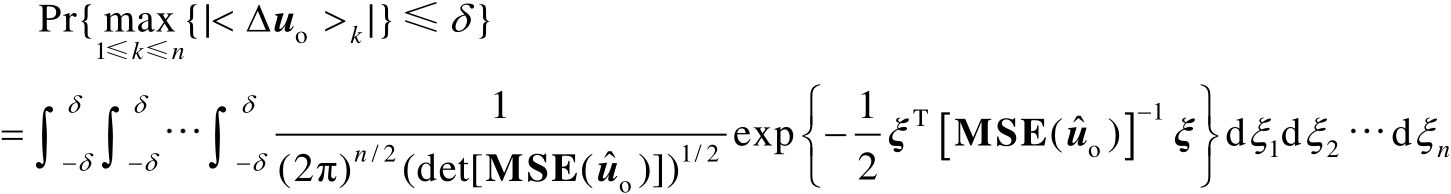
(3.29)
显然,式(3.29)是正方体上的高维积分,可以通过数值运算获得其数值解。
【定义3.2】
若定位误差满足
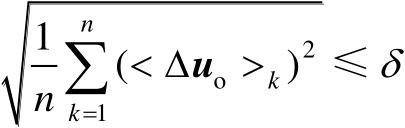 ,则认为是第2类定位成功。
,则认为是第2类定位成功。
第2类定位成功所满足的条件等价为
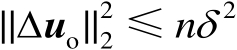 ,于是第2类定位成功概率可以表示为
,于是第2类定位成功概率可以表示为
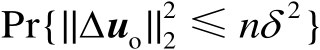 。利用文献[59]中的结论可以得到如下关系式:
。利用文献[59]中的结论可以得到如下关系式:
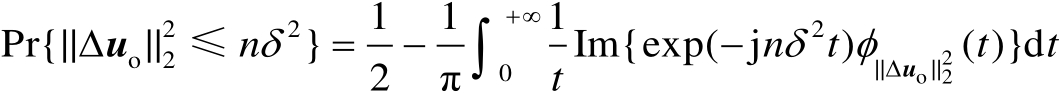
(3.30)
式中,
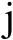 表示虚数单位,满足
表示虚数单位,满足
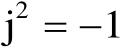 ;
;
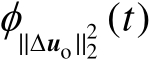 表示随机变量
表示随机变量
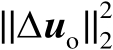 的特征函数。下面需要确定函数
的特征函数。下面需要确定函数
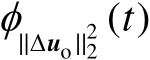 的表达式,具体可见如下命题。
的表达式,具体可见如下命题。
【命题3.7】
若均方误差矩阵
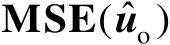 的
的
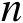 个特征值为
个特征值为
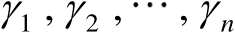 ,则随机变量
,则随机变量
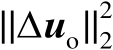 的特征函数可以表示为
的特征函数可以表示为
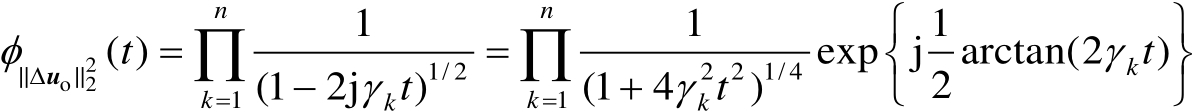
(3.31)
【证明】
令随机向量
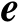 服从均值为零、协方差矩阵为
服从均值为零、协方差矩阵为
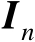 的高斯分布,则有
的高斯分布,则有
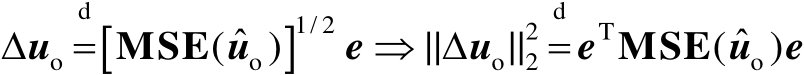
(3.32)
式中,
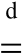 表示两边的随机变量服从相同的概率分布。对矩阵
表示两边的随机变量服从相同的概率分布。对矩阵
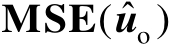 进行特征值分解可得
进行特征值分解可得
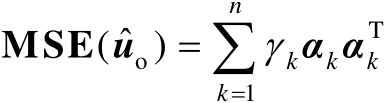
(3.33)
式中,
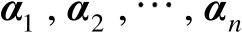 表示对应于特征值
表示对应于特征值
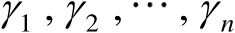 的单位特征向量。将式(3.33)代入式(3.32)中可得
的单位特征向量。将式(3.33)代入式(3.32)中可得
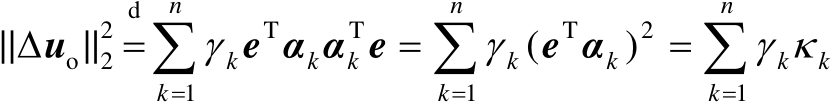
(3.34)
式中,
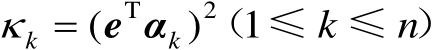 。由于
。由于
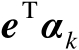 是服从均值为零、方差为1的高斯随机变量,于是随机变量
是服从均值为零、方差为1的高斯随机变量,于是随机变量
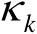 的特征函数为
的特征函数为
 ,而随机变量
,而随机变量
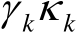 的特征函数为
的特征函数为
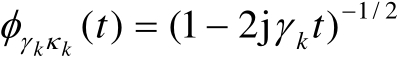 。另一方面,利用对称矩阵特征向量之间的正交性可知,
。另一方面,利用对称矩阵特征向量之间的正交性可知,
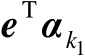 与
与
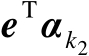 (
(
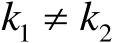 )之间相互统计独立,于是
)之间相互统计独立,于是
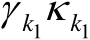 与
与
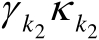 (
(
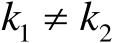 )之间也相互统计独立,由此可得
)之间也相互统计独立,由此可得
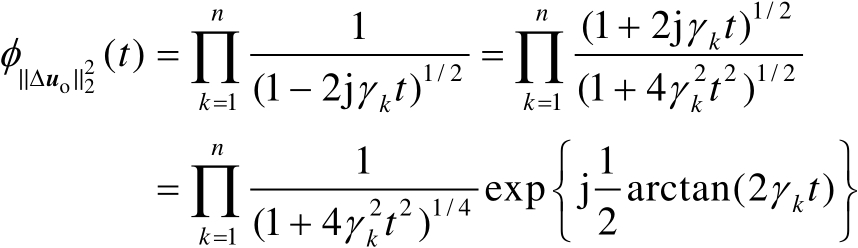
(3.35)
证毕。
将式(3.31)代入式(3.30)中可得
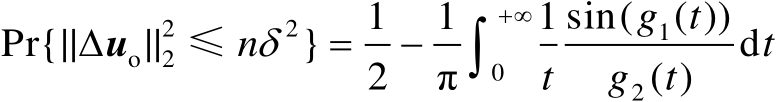
(3.36)
式中
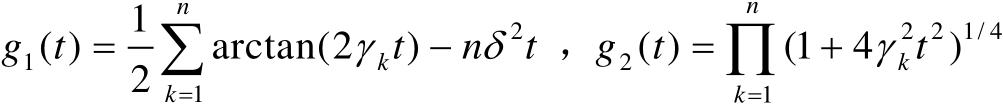
(3.37)
由式(3.36)可知,第2类定位成功概率可以通过一维数值积分来获得,并且其积分区间为
 ,为此需要分析被积分函数在
,为此需要分析被积分函数在
 和
和
 时的取值。首先根据洛必达法则可得
时的取值。首先根据洛必达法则可得
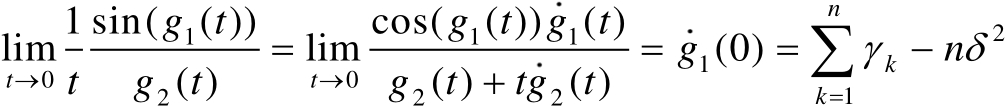
(3.38)
并且不难验证
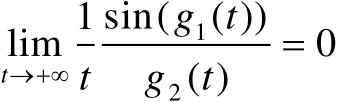
(3.39)
由于当
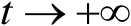 时被积分函数趋于零,因此式(3.36)中的积分上限可以选取一个充分大的正数来逼近。
时被积分函数趋于零,因此式(3.36)中的积分上限可以选取一个充分大的正数来逼近。
【注记3.9】 不难证明,第1类定位成功概率总是小于第2类定位成功概率,这是因为第1类定位成功概率是在正方体内进行积分的,而第2类定位成功概率是在该正方体的外接球内进行积分的,显然第2类积分区域要大于第1类积分区域。
【注记3.10】
根据定义3.1和定义3.2可知,两类定位成功概率均随着
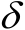 的增加而增加,当
的增加而增加,当
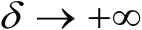 时,无论采用何种定位方法,两类定位成功概率都将趋于1;当
时,无论采用何种定位方法,两类定位成功概率都将趋于1;当
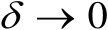 时,无论采用何种定位方法,两类定位成功概率都将趋于0。因此,参数
时,无论采用何种定位方法,两类定位成功概率都将趋于0。因此,参数
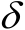 应根据具体的定位场景和需求来选取。
应根据具体的定位场景和需求来选取。