




克拉美罗界给出了任意无偏估计器的估计均方误差的理论下界 [56] 。由于无线信号定位问题本质上属于参数估计问题,因此定位方法的理论下界可以通过克拉美罗界来获得。本节将在多种场景下给出定位问题克拉美罗界的理论表达式,从而为后续章节中各种定位方法的理论性能提供参考。表3.1罗列了不同定位场景下的克拉美罗界数学符号,以便于读者区分。
表3.1 不同定位场景下的克拉美罗界数学符号

假设有
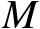 个传感器利用一种或多种观测量对单个辐射源进行定位,其中第
个传感器利用一种或多种观测量对单个辐射源进行定位,其中第
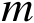 个传感器的位置向量为
个传感器的位置向量为
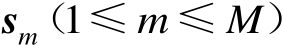 ,它们均精确已知;辐射源的位置向量为
,它们均精确已知;辐射源的位置向量为
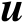 ,它是未知量。用于辐射源定位的观测模型可以统一表示为
,它是未知量。用于辐射源定位的观测模型可以统一表示为
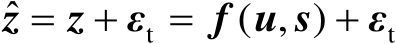
(3.1)
式中,
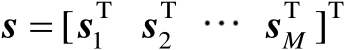 表示由全部传感器位置构成的向量;
表示由全部传感器位置构成的向量;
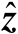 表示含有观测误差的定位观测量;
表示含有观测误差的定位观测量;
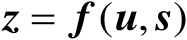 表示没有观测误差的精确定位观测量,其中
表示没有观测误差的精确定位观测量,其中
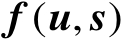 表示关于向量
表示关于向量
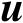 和
和
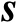 的连续可导函数,其具体的代数形式取决于所采用的定位观测量;
的连续可导函数,其具体的代数形式取决于所采用的定位观测量;
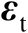 表示观测误差,假设其服从零均值的高斯分布,并且协方差矩阵为
表示观测误差,假设其服从零均值的高斯分布,并且协方差矩阵为
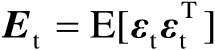 。
。
基于观测模型式(3.1)可以得到传感器位置向量
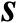 精确已知条件下,估计辐射源位置向量
精确已知条件下,估计辐射源位置向量
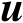 的克拉美罗界,具体可见如下命题。
的克拉美罗界,具体可见如下命题。
【命题3.1】
基于观测模型式(3.1),辐射源位置向量
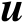 的估计均方误差的克拉美罗界矩阵可以表示为
的估计均方误差的克拉美罗界矩阵可以表示为
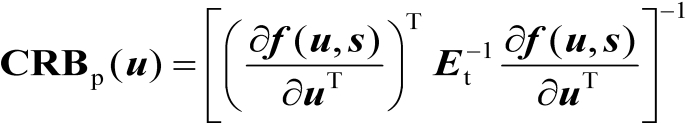
(3.2)
式中,
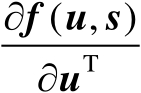 为Jacobian矩阵。
为Jacobian矩阵。
命题3.1的证明见文献[57,58]。
【注记3.1】
由式(3.2)可知,克拉美罗界
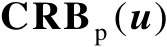 若要存在,Jacobian矩阵
若要存在,Jacobian矩阵
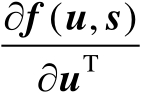 必须是列满秩的,否则该定位问题不可解。
必须是列满秩的,否则该定位问题不可解。
【注记3.2】
由式(3.2)可知,Jacobian矩阵
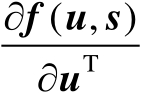 的数值越大,克拉美罗界
的数值越大,克拉美罗界
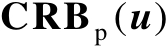 就越小,此时的定位精度就越高。
就越小,此时的定位精度就越高。
假设在实际定位中传感器位置并不能精确已知,也就是说传感器位置观测值与其真实值之间存在观测误差,相应的观测模型可以表示为
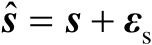
(3.3)
式中,
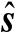 表示传感器位置向量的观测值;
表示传感器位置向量的观测值;
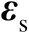 表示观测误差,假设其服从零均值的高斯分布,并且协方差矩阵为
表示观测误差,假设其服从零均值的高斯分布,并且协方差矩阵为
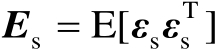 ,此外,误差向量
,此外,误差向量
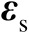 与
与
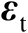 之间相互统计独立。
之间相互统计独立。
结合式(3.1)和式(3.3)可知,在传感器位置误差存在条件下,用于辐射源定位的观测模型可以联立表示为
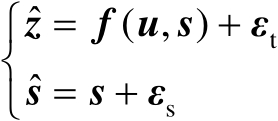
(3.4)
观测模型式(3.4)中的未知参数同时包含
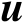 和
和
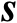 ,其联合估计的克拉美罗界可见如下命题。
,其联合估计的克拉美罗界可见如下命题。
【命题3.2】
基于观测模型式(3.4),未知参数
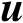 和
和
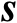 的联合估计均方误差的克拉美罗界矩阵可以表示为
的联合估计均方误差的克拉美罗界矩阵可以表示为
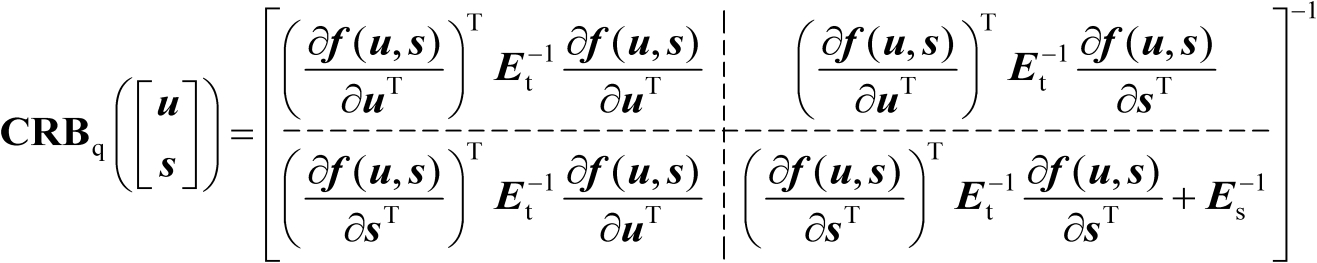
(3.5)
式中,
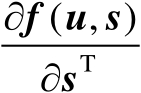 为Jacobian矩阵。
为Jacobian矩阵。
命题3.2的证明见文献[57,58]。利用式(3.5)还可以进一步推得辐射源位置向量
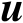 的估计均方误差的克拉美罗界矩阵,下面给出其两种表达式。
的估计均方误差的克拉美罗界矩阵,下面给出其两种表达式。
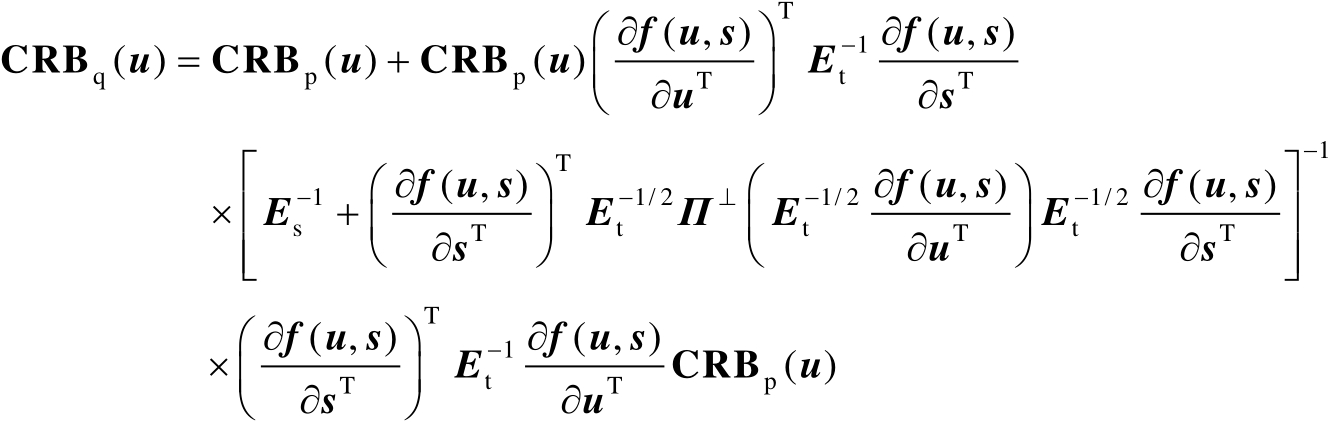
(3.6)
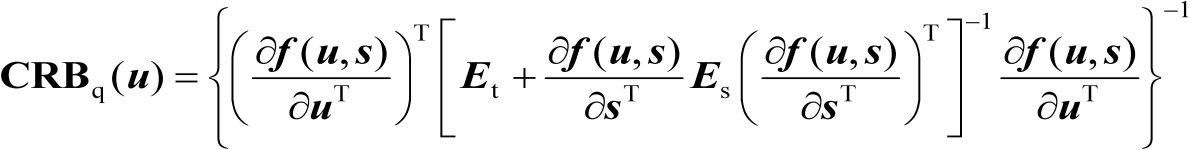
(3.7)
式(3.6)和式(3.7)的证明见文献[57,58]。
【注记3.3】
对比式(3.2)和式(3.7)可知,传感器位置误差
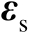 的影响可以等效为增加了观测向量
的影响可以等效为增加了观测向量
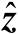 中的观测误差,并且是将观测误差的协方差矩阵由原先的
中的观测误差,并且是将观测误差的协方差矩阵由原先的
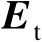 增加至
增加至
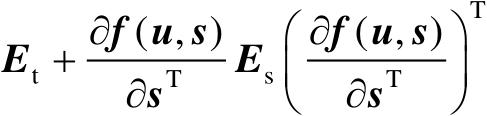 ,由此可以得到关系式
,由此可以得到关系式
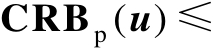
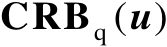 。当然,该关系式也可以直接通过式(3.6)获得。
。当然,该关系式也可以直接通过式(3.6)获得。
假设需要对区域内的
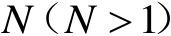 个辐射源进行定位,其中第
个辐射源进行定位,其中第
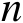 个辐射源的位置向量为
个辐射源的位置向量为
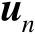 ,它是未知量。类似于式(3.1),针对第
,它是未知量。类似于式(3.1),针对第
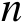 个辐射源的观测模型可以统一表示为
个辐射源的观测模型可以统一表示为
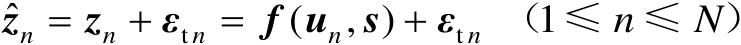
(3.8)
式中,
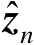 表示含有观测误差的定位观测量;
表示含有观测误差的定位观测量;
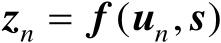 表示没有观测误差的精确定位观测量;
表示没有观测误差的精确定位观测量;
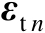 表示观测误差,假设其服从零均值的高斯分布,并且协方差矩阵为
表示观测误差,假设其服从零均值的高斯分布,并且协方差矩阵为
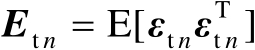 ,此外,误差向量组
,此外,误差向量组
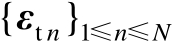 相互间统计独立,也就是考虑对多个不相关源进行定位。
相互间统计独立,也就是考虑对多个不相关源进行定位。
在实际定位中,不同的辐射源对应相同的传感器位置误差,此时应该对
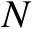 个辐射源进行协同定位,以获得协同增益。为了给出多辐射源协同定位情形下的克拉美罗界,需要首先将式(3.8)中的
个辐射源进行协同定位,以获得协同增益。为了给出多辐射源协同定位情形下的克拉美罗界,需要首先将式(3.8)中的
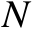 个等式进行合并,如下式所示:
个等式进行合并,如下式所示:
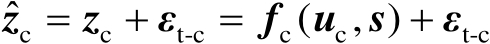
(3.9)
式中
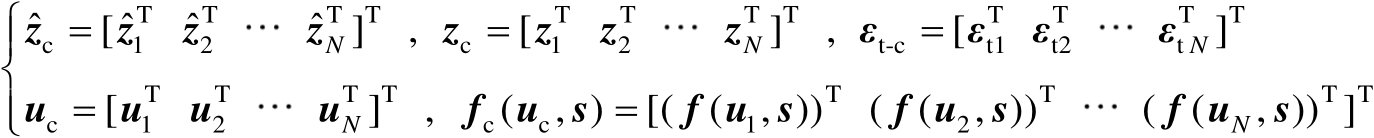
(3.10)
假设观测误差向量
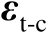 服从零均值的高斯分布,并且其协方差矩阵为
服从零均值的高斯分布,并且其协方差矩阵为
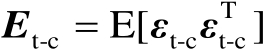 。对于不相关源而言,满足
。对于不相关源而言,满足
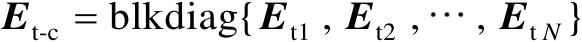 。另一方面,这里将
。另一方面,这里将
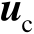 称为多辐射源位置向量。所谓多辐射源协同定位就是直接估计向量
称为多辐射源位置向量。所谓多辐射源协同定位就是直接估计向量
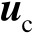 ,而不是独立地估计每个辐射源位置向量
,而不是独立地估计每个辐射源位置向量
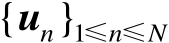 。
。
结合式(3.3)和式(3.9)可知,在传感器位置误差存在条件下,用于多辐射源协同定位的观测模型可以联立表示为
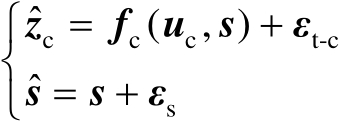
(3.11)
观测模型式(3.11)中的未知参数同时包含
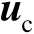 和
和
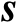 ,其联合估计的克拉美罗界可见如下命题。
,其联合估计的克拉美罗界可见如下命题。
【命题3.3】
基于观测模型式(3.11),未知参数
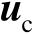 和
和
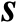 的联合估计均方误差的克拉美罗界矩阵可以表示为
的联合估计均方误差的克拉美罗界矩阵可以表示为
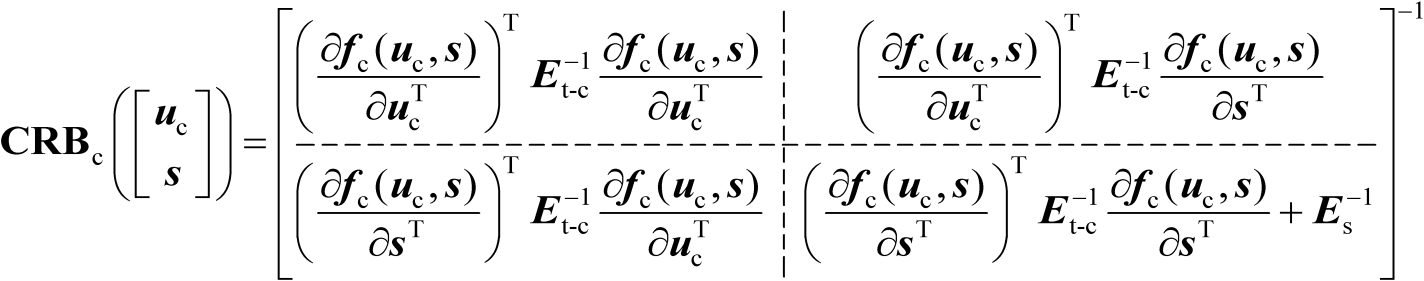
(3.12)
式中
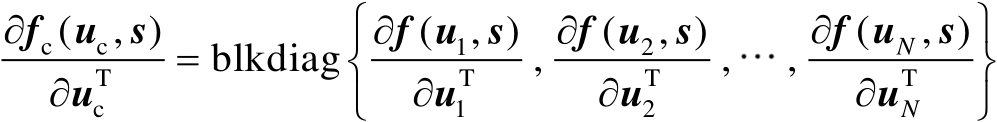
(3.13)
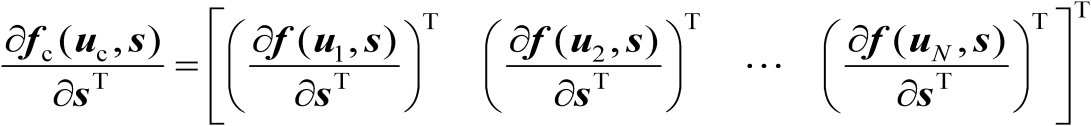
(3.14)
命题3.3的证明与命题3.2的证明类似。利用式(3.12)还可以进一步推得多辐射源位置向量
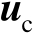 的估计均方误差的克拉美罗界矩阵,下面给出其两种表达式。
的估计均方误差的克拉美罗界矩阵,下面给出其两种表达式。
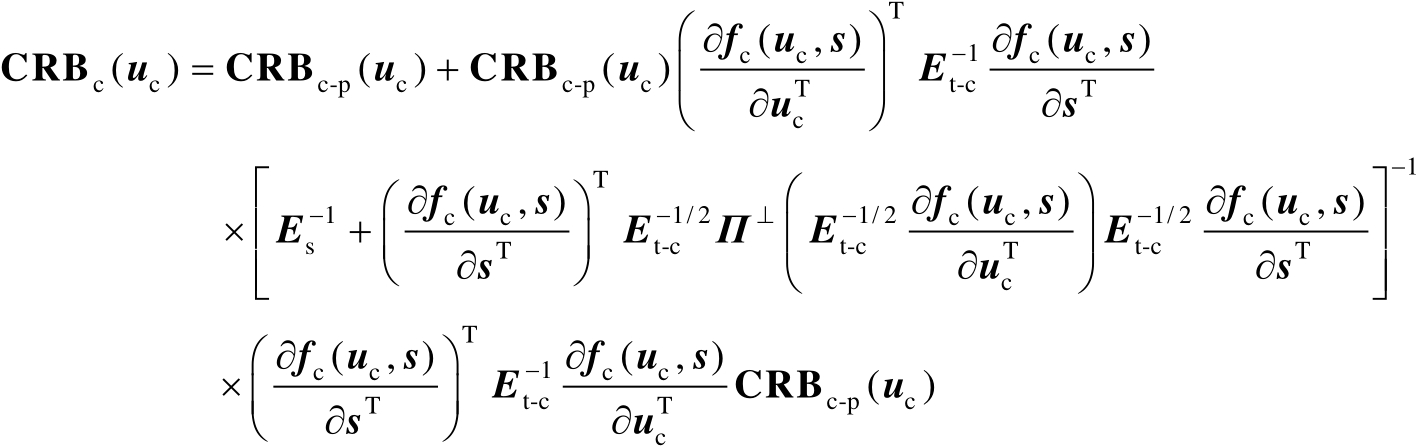
(3.15)
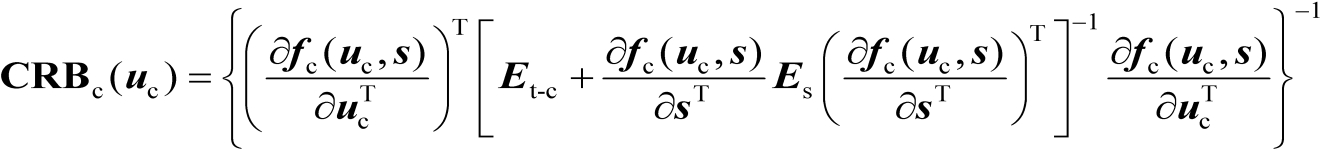
(3.16)
式中
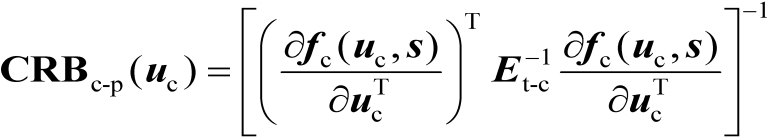
(3.17)
式(3.15)和式(3.16)的证明分别与式(3.6)和式(3.7)的证明类似,具体证明见文献[57,58]。
【注记3.4】
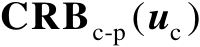 可看作在传感器位置精确已知条件下,多辐射源协同定位的克拉美罗界矩阵。
可看作在传感器位置精确已知条件下,多辐射源协同定位的克拉美罗界矩阵。
前面曾指出,在传感器位置误差存在条件下,多辐射源协同定位有助于提高对每个辐射源的定位精度,可以通过定量比较两种克拉美罗界来说明此结论。
在多辐射源协同定位情形下,将第
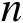 个辐射源位置向量
个辐射源位置向量
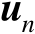 的估计均方误差的克拉美罗界矩阵记为
的估计均方误差的克拉美罗界矩阵记为
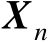 ,于是基于式(3.16)可知
,于是基于式(3.16)可知
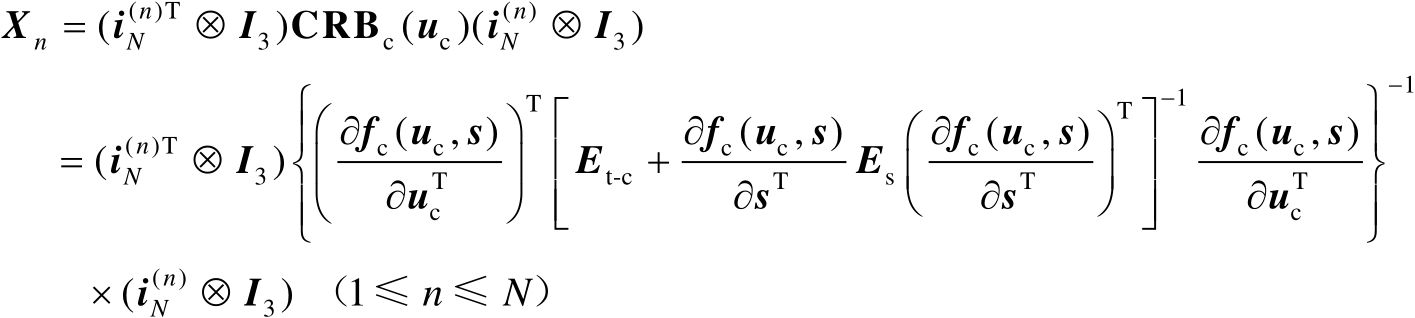
(3.18)
若独立地对
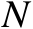 个辐射源进行定位,将第
个辐射源进行定位,将第
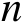 个辐射源位置向量
个辐射源位置向量
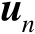 的估计均方误差的克拉美罗界矩阵记为
的估计均方误差的克拉美罗界矩阵记为
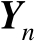 ,则由式(3.7)可得
,则由式(3.7)可得
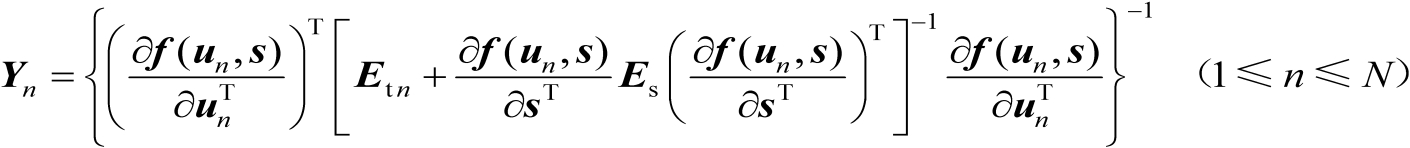
(3.19)
比较式(3.18)和式(3.19)可以得到如下命题。
【命题3.4】
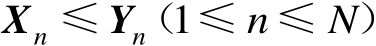 ,当且仅当
,当且仅当
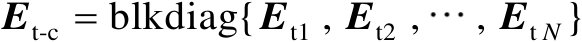 和
和
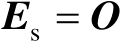 时,
时,
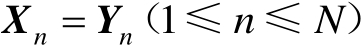 。
。
命题3.4的证明见文献[55,57]。
假设在定位区域内存在某个校正源,它既可以是人为主动放置的,也可以是一些信息公开的信号源,因此校正源的位置向量是精确已知的,利用该校正源的位置信息可以有效抑制传感器位置误差对辐射源定位精度的影响。
将校正源的位置向量记为
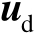 ,针对校正源的观测模型可以统一表示为
,针对校正源的观测模型可以统一表示为
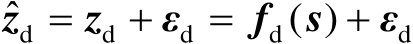
(3.20)
式中,
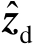 表示含有观测误差的观测量;
表示含有观测误差的观测量;
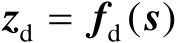 表示没有观测误差的精确观测量,其中
表示没有观测误差的精确观测量,其中
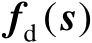 表示关于向量
表示关于向量
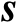 的连续可导函数,其具体的代数形式取决于所采用的观测量
[1]
;
的连续可导函数,其具体的代数形式取决于所采用的观测量
[1]
;
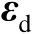 表示观测误差,假设其服从零均值的高斯分布,并且协方差矩阵为
表示观测误差,假设其服从零均值的高斯分布,并且协方差矩阵为
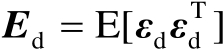 ,此外,误差向量
,此外,误差向量
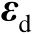 、
、
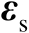 及
及
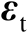 之间相互统计独立。
之间相互统计独立。
结合式(3.1)、式(3.3)及式(3.20)可知,在校正源和传感器位置误差存在条件下,用于辐射源定位的观测模型可以联立表示为
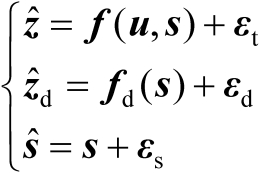
(3.21)
观测模型式(3.21)中的未知参数同时包含
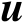 和
和
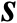 ,其联合估计的克拉美罗界可见如下命题。
,其联合估计的克拉美罗界可见如下命题。
【命题3.5】
基于观测模型式(3.21),未知参数
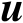 和
和
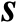 的联合估计均方误差的克拉美罗界矩阵可以表示为
的联合估计均方误差的克拉美罗界矩阵可以表示为
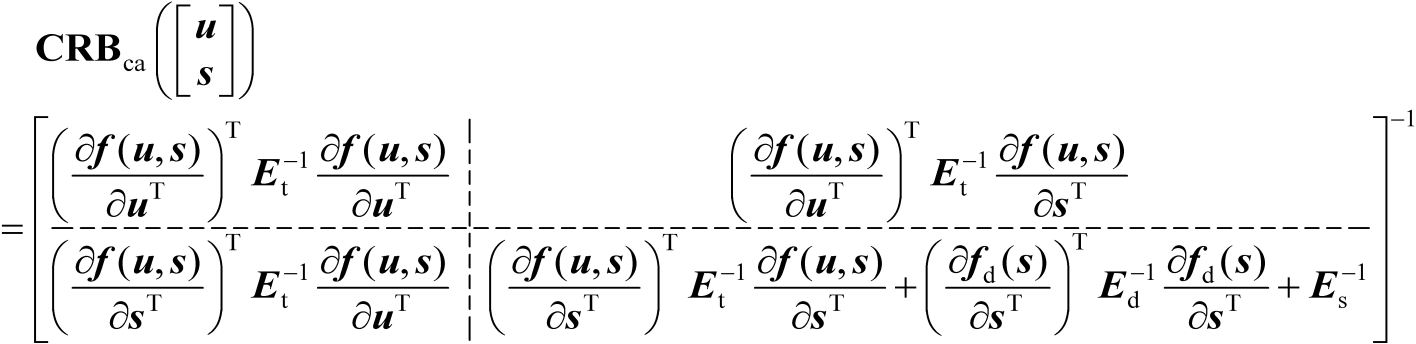
(3.22)
式中,
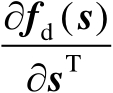 为Jacobian矩阵。
为Jacobian矩阵。
命题3.5的证明见文献[57,58]。利用式(3.22)可以进一步推得辐射源位置向量
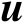 的估计均方误差的克拉美罗界矩阵,如下式所示:
的估计均方误差的克拉美罗界矩阵,如下式所示:
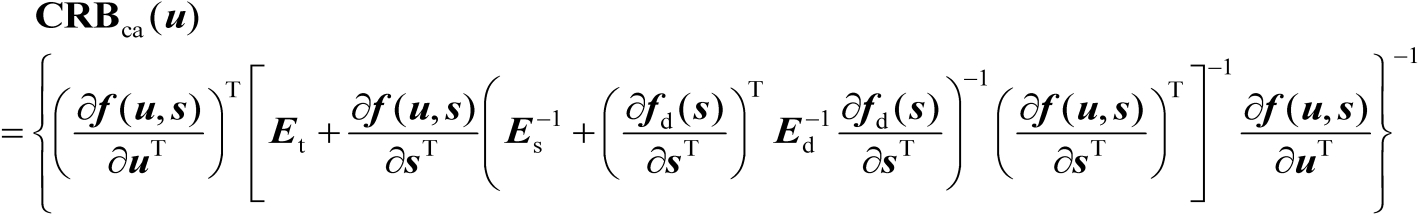
(3.23)
式(3.23)的证明见文献[57,58]。
【注记3.5】
对比式(3.7)和式(3.23)可知,相比于没有校正源的情形,校正源观测量
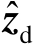 有助于减小传感器位置误差的影响,其作用可以等效为将传感器位置误差的协方差矩阵由原先的
有助于减小传感器位置误差的影响,其作用可以等效为将传感器位置误差的协方差矩阵由原先的
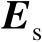 降低至
降低至
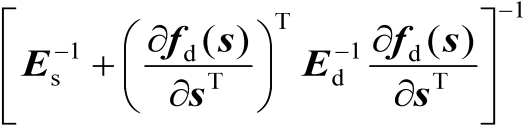 ,于是有
,于是有
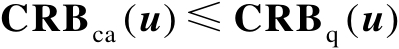 。
。
【注记3.6】
对比式(3.2)和式(3.23)可知,
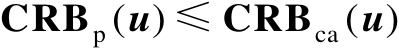 。若Jacobian矩阵
。若Jacobian矩阵
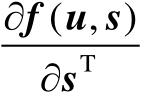 是行满秩的,则有
是行满秩的,则有
 ,这意味着虽然利用校正源观测量可以提高辐射源的定位精度,但无法将精度提升至传感器位置精确已知情形下的定位精度。
,这意味着虽然利用校正源观测量可以提高辐射源的定位精度,但无法将精度提升至传感器位置精确已知情形下的定位精度。
利用式(3.22)还可以进一步推得传感器位置向量
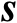 的估计均方误差的克拉美罗界矩阵,如下式所示:
的估计均方误差的克拉美罗界矩阵,如下式所示:
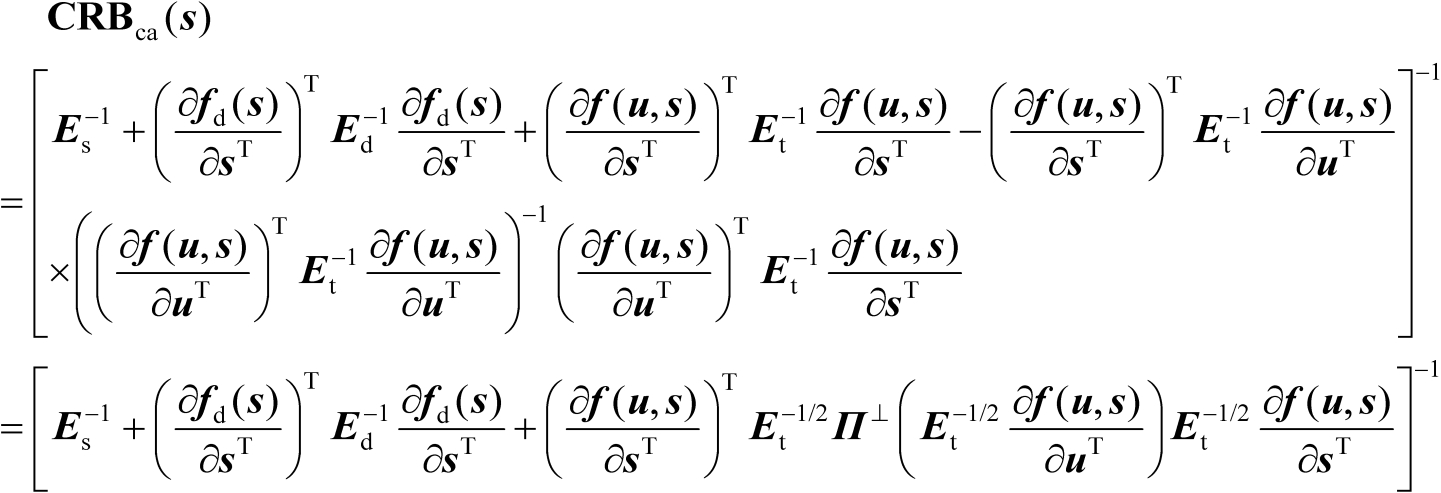
(3.24)
下面给出在仅有校正源观测量的条件下,传感器位置向量
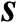 的估计均方误差的克拉美罗界矩阵。结合式(3.3)和式(3.20)可得观测模型为
的估计均方误差的克拉美罗界矩阵。结合式(3.3)和式(3.20)可得观测模型为
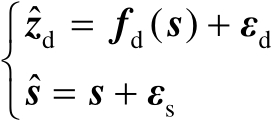
(3.25)
观测模型式(3.25)中的未知参数仅包括
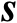 ,其估计的克拉美罗界可见如下命题。
,其估计的克拉美罗界可见如下命题。
【命题3.6】
基于观测模型式(3.25),未知参数
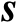 的估计均方误差的克拉美罗界矩阵可以表示为
的估计均方误差的克拉美罗界矩阵可以表示为
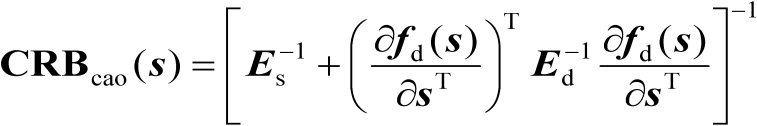
(3.26)
命题3.6的证明见文献[58]。
【注记3.7】
由式(3.26)可知,
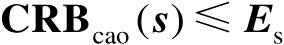 ,这意味着利用校正源观测量可以提高传感器位置向量
,这意味着利用校正源观测量可以提高传感器位置向量
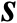 的估计精度(相比于其先验观测量
的估计精度(相比于其先验观测量
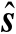 而言)。
而言)。
【注记3.8】
对比式(3.24)和式(3.26)可知,
 ,这意味着利用辐射源观测量同样有助于提高传感器位置向量
,这意味着利用辐射源观测量同样有助于提高传感器位置向量
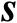 的估计精度。
的估计精度。