




本节将介绍关于估计器误差分析的预备知识。如果观测误差存在,估计器的估计结果通常会偏离真实值,从而产生估计误差。当研究一种估计器的估计误差时,通常使用一阶误差分析方法,因为该方法可以将估计误差表示成关于观测误差的线性函数,从而能够进一步获得该估计器的均方误差。下面将分别针对无等式约束和含有等式约束两种情形下的一阶误差分析进行讨论。
考虑下面两种估计器:
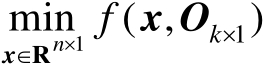
(2.79)
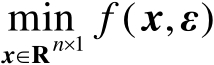
(2.80)
式(2.79)表示无观测误差条件(即理想条件)下的估计器,假设其最优解为
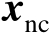 ,由于其中没有观测误差,因此该最优解等于未知参量的真实值;式(2.80)表示观测误差存在条件下的估计器,其中
,由于其中没有观测误差,因此该最优解等于未知参量的真实值;式(2.80)表示观测误差存在条件下的估计器,其中
 为观测误差,该误差的存在必然使式(2.80)的最优解不再为真实值
为观测误差,该误差的存在必然使式(2.80)的最优解不再为真实值
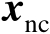 ,不妨令其最优解为
,不妨令其最优解为
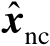 ,并将其估计误差记为
,并将其估计误差记为
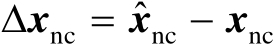 。实际应用中使用的估计器通常是式(2.80),因为观测误差
。实际应用中使用的估计器通常是式(2.80),因为观测误差
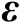 的存在不可避免。
的存在不可避免。
为了获得估计值
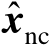 的统计特性,需要推导估计误差
的统计特性,需要推导估计误差
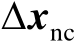 与观测误差
与观测误差
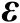 之间的闭式关系。然而,当目标函数是非线性函数时,精确的闭式关系将难以获得,只能得到其近似关系。一阶误差分析的目的是要给出
之间的闭式关系。然而,当目标函数是非线性函数时,精确的闭式关系将难以获得,只能得到其近似关系。一阶误差分析的目的是要给出
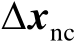 与
与
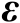 之间的线性关系,该方法在小观测误差情形下可以获得较好的性能预测精度。
之间的线性关系,该方法在小观测误差情形下可以获得较好的性能预测精度。
通过两种方法可以得到
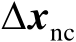 和
和
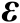 之间的线性关系,并且它们的分析结果是一致的,下面将分别加以讨论。
之间的线性关系,并且它们的分析结果是一致的,下面将分别加以讨论。
首先介绍第1种方法,结合式(2.79)、式(2.80)及极值原理可得
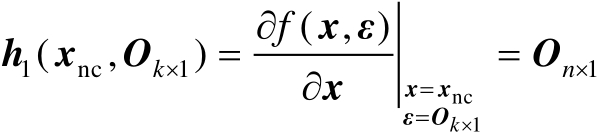
(2.81)
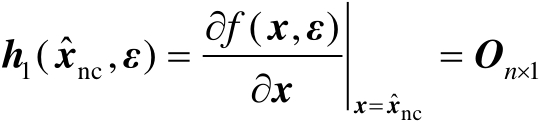
(2.82)
将
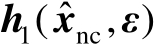 在点
在点
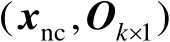 处进行一阶泰勒级数展开可知
处进行一阶泰勒级数展开可知
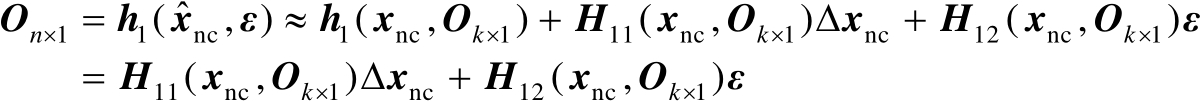
(2.83)
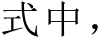
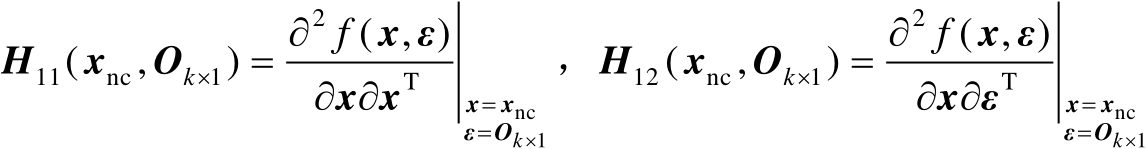 。式(2.83)中第3个等号处的运算利用了式(2.81),基于式(2.83)可以进一步推得
。式(2.83)中第3个等号处的运算利用了式(2.81),基于式(2.83)可以进一步推得
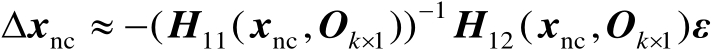
(2.84)
式(2.84)刻画了
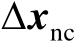 和
和
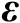 之间的线性关系。若误差向量
之间的线性关系。若误差向量
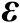 服从零均值的高斯分布,并且其协方差矩阵为
服从零均值的高斯分布,并且其协方差矩阵为
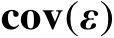 ,那么估计误差
,那么估计误差
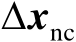 也近似服从零均值的高斯分布,并且其协方差矩阵为
也近似服从零均值的高斯分布,并且其协方差矩阵为
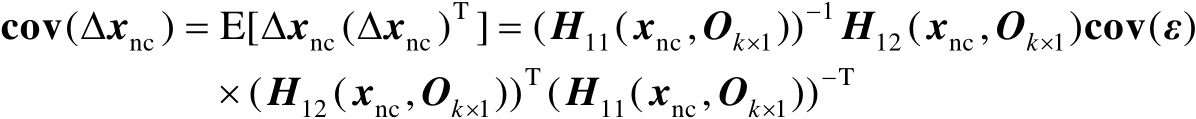
(2.85)
接着介绍第2种方法,该方法需要将
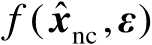 在点
在点
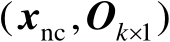 处进行二阶泰勒级数展开,如下式所示:
处进行二阶泰勒级数展开,如下式所示:
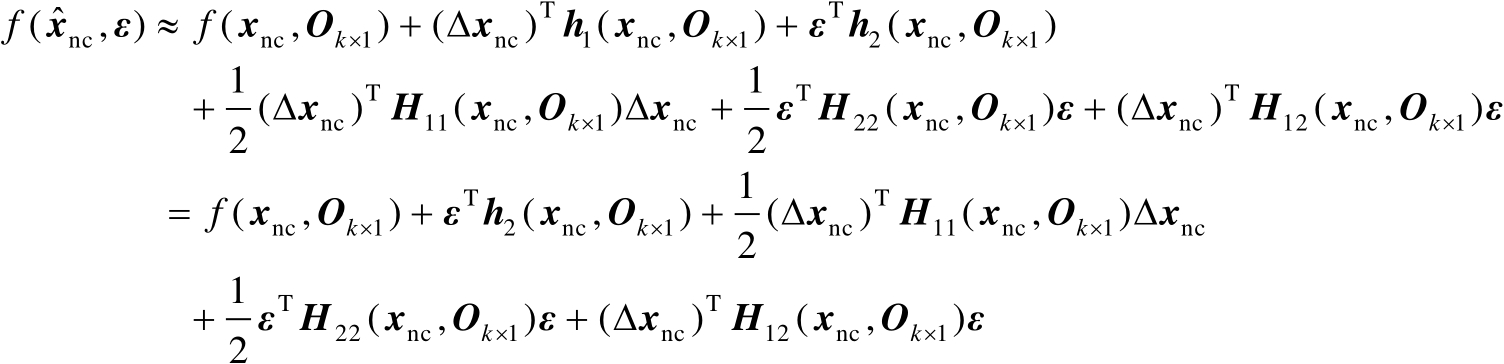
(2.86)
式中,
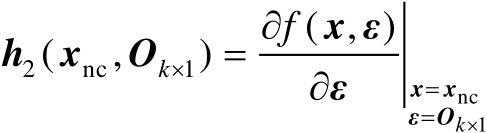 ,
,
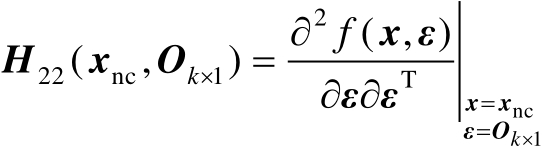 。式(2.86)中第2个等号处的运算利用了式(2.81)。由式(2.80)可知
。式(2.86)中第2个等号处的运算利用了式(2.81)。由式(2.80)可知
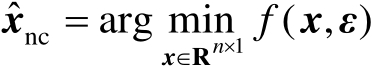 ,再结合式(2.86)可得
,再结合式(2.86)可得
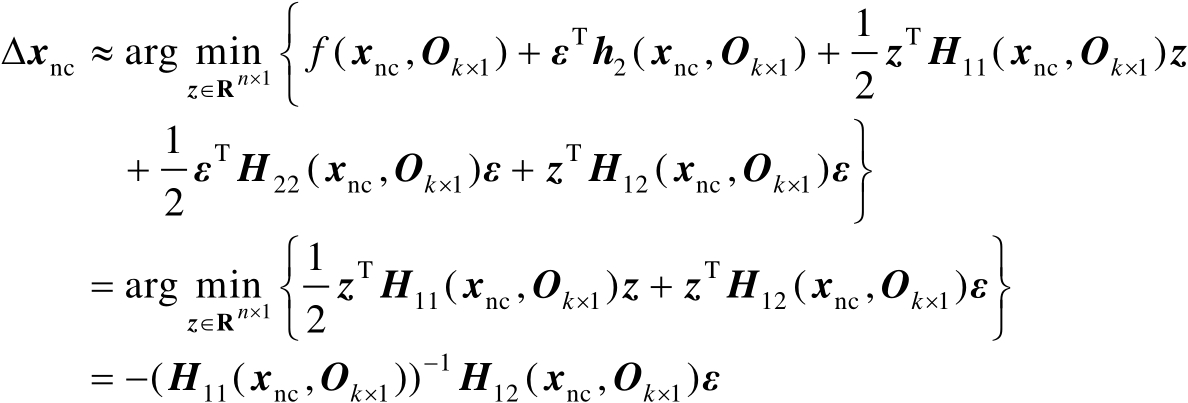
(2.87)
式(2.84)和式(2.87)给出了相同的表达式,因此上面两种方法得到的估计误差的统计特性是一致的。
下面讨论另一类更为复杂的估计器,其中的未知参量需要服从等式约束。考虑下面两种估计器:
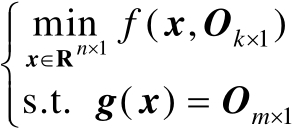
(2.88)
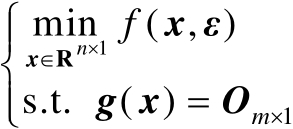
(2.89)
式(2.88)表示无观测误差条件(即理想条件)下的估计器,假设其最优解为
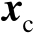 ,由于其中没有观测误差,因此该最优解等于未知参量的真实值;式(2.89)表示观测误差存在条件下的估计器,观测误差的存在必然使得式(2.89)的最优解不再为真实值
,由于其中没有观测误差,因此该最优解等于未知参量的真实值;式(2.89)表示观测误差存在条件下的估计器,观测误差的存在必然使得式(2.89)的最优解不再为真实值
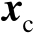 ,不妨令其最优解为
,不妨令其最优解为
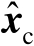 ,并将其估计误差记为
,并将其估计误差记为
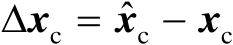 。由于
。由于
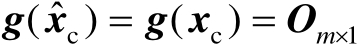 ,由此可以推得估计误差
,由此可以推得估计误差
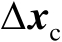 近似满足
近似满足
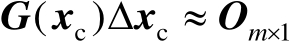
(2.90)
式中,
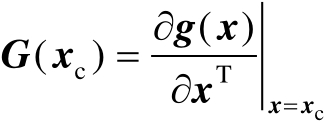 表示向量函数
表示向量函数
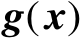 的Jacobian矩阵在
的Jacobian矩阵在
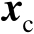 处的取值,假设该矩阵是行满秩的。结合式(2.87)和式(2.90)可知,在一阶误差分析框架下,估计误差
处的取值,假设该矩阵是行满秩的。结合式(2.87)和式(2.90)可知,在一阶误差分析框架下,估计误差
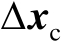 应是如下约束优化问题的最优解:
应是如下约束优化问题的最优解:
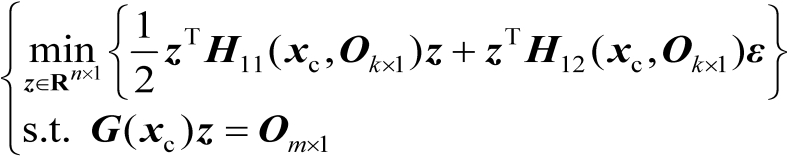
(2.91)
根据2.2节中的讨论可知,式(2.91)可以利用拉格朗日乘子法进行求解,相应的拉格朗日函数为
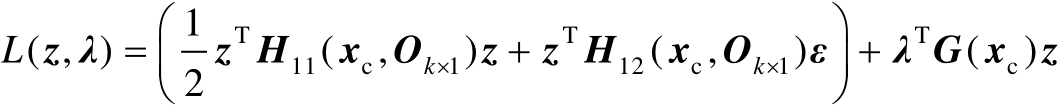
(2.92)
根据式(2.59)可知,最优解
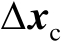 和
和
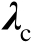 应满足如下等式:
应满足如下等式:
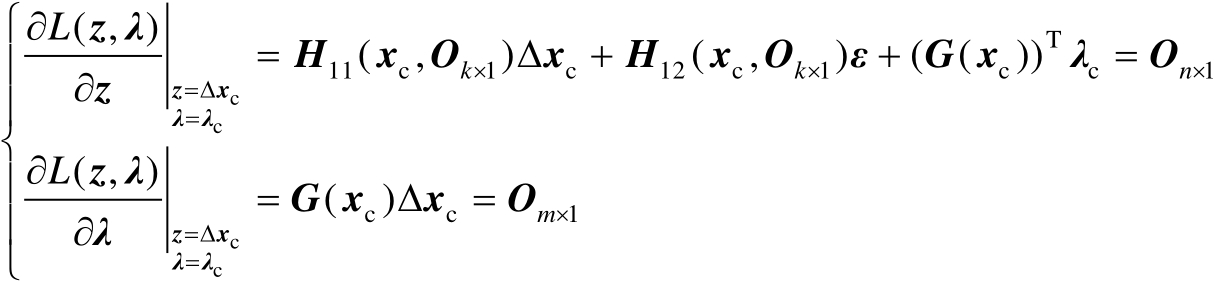
(2.93)
由式(2.93)中的第1式可得
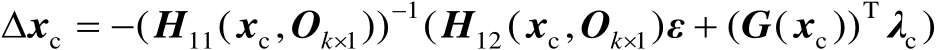
(2.94)
将式(2.94)代入式(2.93)中的第2式可得
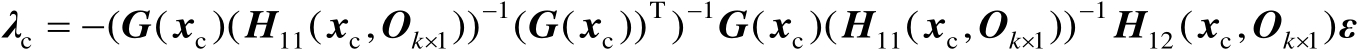
(2.95)
最后将式(2.95)代入式(2.94)中可得
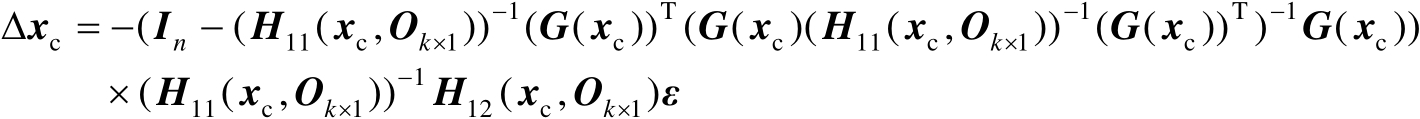
(2.96)
式(2.96)刻画了
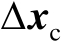 与
与
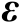 之间的线性关系。若误差向量
之间的线性关系。若误差向量
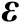 服从零均值的高斯分布,并且其协方差矩阵为
服从零均值的高斯分布,并且其协方差矩阵为
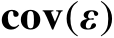 ,那么估计误差
,那么估计误差
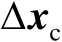 也近似服从零均值的高斯分布,其协方差矩阵为
也近似服从零均值的高斯分布,其协方差矩阵为
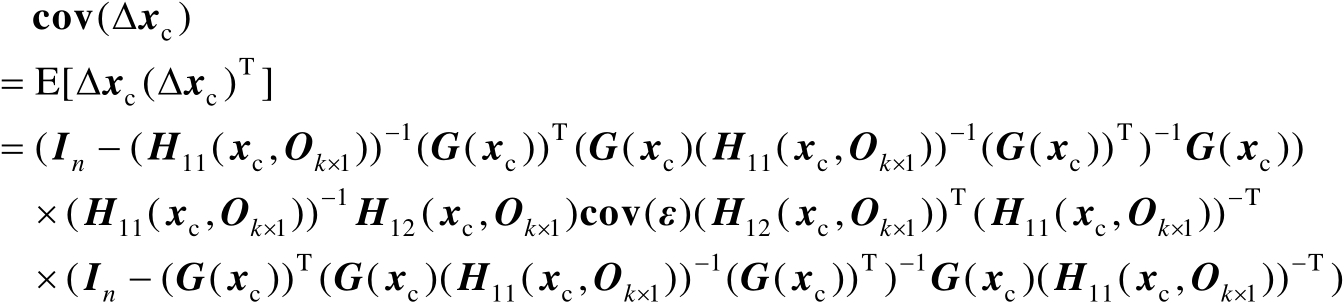
(2.97)
需要指出的是,在本书讨论的问题中,
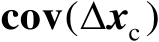 的表达式能够得到进一步简化。
的表达式能够得到进一步简化。