




本节将介绍关于矩阵扰动分析的预备知识。所谓矩阵扰动分析,就是将一个受到误差扰动的矩阵表示成关于误差项的闭式形式(通常是多项式形式),在误差不是很大的情况下,通常保留误差的一阶项即可,该方法可称为一阶扰动分析,这也是本书中主要采取的方法。
首先给出一个关于逆矩阵求导的结论,具体可见如下命题。
【命题2.15】
设矩阵
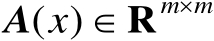 是关于标量
是关于标量
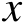 的连续可导函数,并且
的连续可导函数,并且
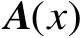 可逆,则有如下导数关系式:
可逆,则有如下导数关系式:
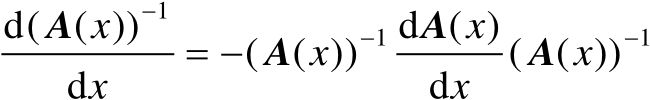
(2.71)
【证明】
首先根据逆矩阵的定义可知
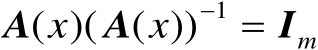 ,将该等式两边对
,将该等式两边对
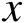 求导可得
求导可得
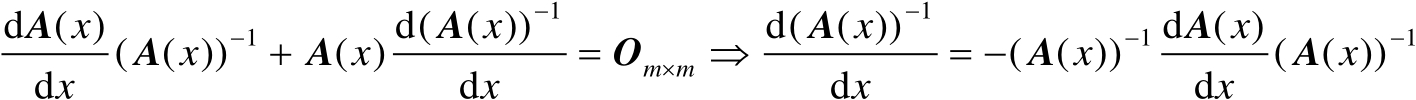
(2.72)
证毕。
基于命题2.15可以得到如下结论。
【命题2.16】
设可逆矩阵
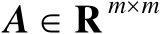 ,该矩阵受到误差矩阵
,该矩阵受到误差矩阵
 的扰动变为
的扰动变为
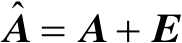 ,并假设
,并假设
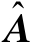 仍然为可逆矩阵,则有如下关系式:
仍然为可逆矩阵,则有如下关系式:
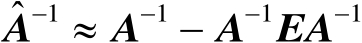
(2.73)
式中省略的项为误差矩阵
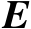 的二阶及其以上各阶项。
的二阶及其以上各阶项。
【证明】
首先可以将矩阵
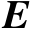 表示为
表示为
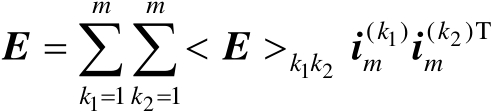
(2.74)
然后结合一阶泰勒级数展开和式(2.71)可得
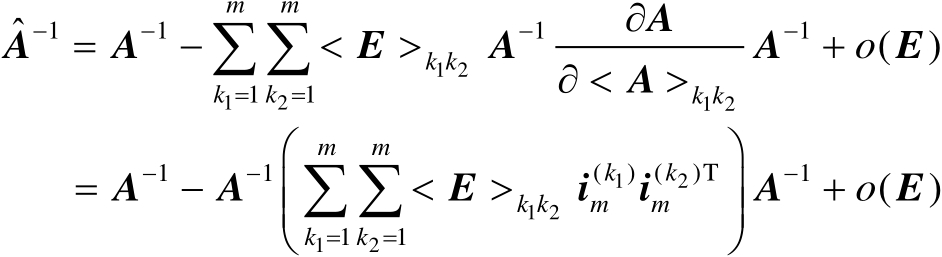
(2.75)
式中,
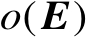 表示误差矩阵
表示误差矩阵
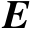 的二阶及其以上各阶项。将式(2.74)代入式(2.75),可知式(2.73)成立。证毕。
的二阶及其以上各阶项。将式(2.74)代入式(2.75),可知式(2.73)成立。证毕。
当有多个受到误差扰动的矩阵相乘时,一阶扰动分析方法可以忽略各个误差矩阵之间的交叉项,下面总结一些主要结论。
设矩阵
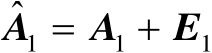 ,
,
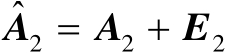 ,
,
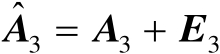 ,其中
,其中
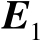 、
、
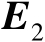 及
及
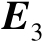 均为误差矩阵,
均为误差矩阵,
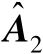 和
和
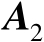 均为可逆矩阵。在一阶扰动分析框架下可以得到如下一系列关系式:
均为可逆矩阵。在一阶扰动分析框架下可以得到如下一系列关系式:
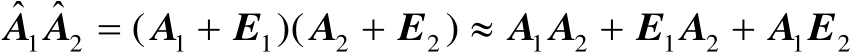
(2.76)
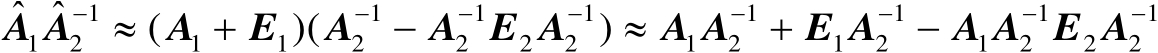
(2.77)
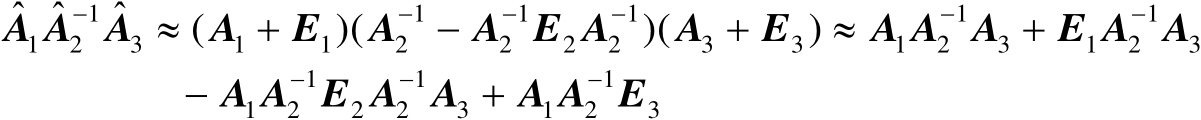
(2.78)
式(2.76)~式(2.78)将在本书中多次使用。