




本节将介绍关于拉格朗日乘子法的预备知识,拉格朗日乘子法可用于求解含等式约束的优化问题。
1.基本原理
含等式约束优化问题的数学模型为
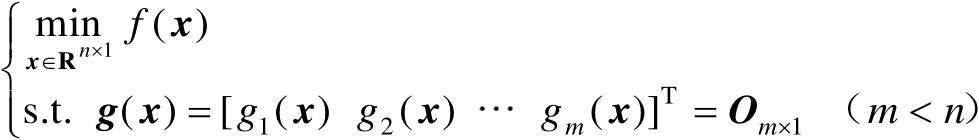
(2.51)
式(2.51)的求解方法可见如下命题。
【命题2.14】
设
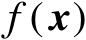 和
和
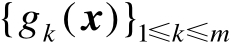 均为连续一阶可导函数,记向量
均为连续一阶可导函数,记向量
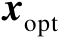 是式(2.51)的局部最优解,
是式(2.51)的局部最优解,
 是
是
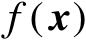 的梯度向量(即有
的梯度向量(即有
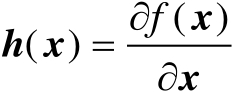 ),
),
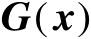 是函数
是函数
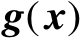 的Jacobian矩阵(即有
的Jacobian矩阵(即有
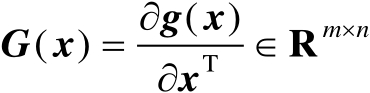 ),并且
),并且
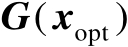 是行满秩矩阵,则存在
是行满秩矩阵,则存在
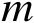 维列向量
维列向量
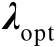 满足
满足
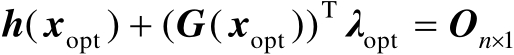
(2.52)
【证明】
由于向量
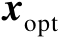 是式(2.51)的局部最优解,它一定也是可行解,于是满足
是式(2.51)的局部最优解,它一定也是可行解,于是满足
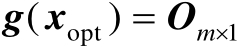 。另一方面,由于
。另一方面,由于
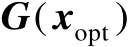 是
是
 阶行满秩矩阵,其中必然存在
阶行满秩矩阵,其中必然存在
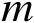 阶子矩阵是可逆的,不失一般性,假设其中前
阶子矩阵是可逆的,不失一般性,假设其中前
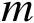 列构成的子矩阵可逆,则根据隐函数定理可知,在
列构成的子矩阵可逆,则根据隐函数定理可知,在
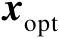 的某个
的某个
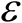 -领域内,基于方程组
-领域内,基于方程组
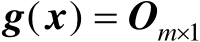 可以确定将
可以确定将
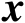 的前
的前
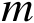 个变量
个变量
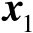 表示成关于其后
表示成关于其后
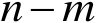 个变量
个变量
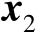 的闭式函数,不妨将该函数记为
的闭式函数,不妨将该函数记为
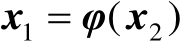 ,于是下面仅需要考虑对向量
,于是下面仅需要考虑对向量
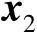 进行优化即可。
进行优化即可。
现将矩阵
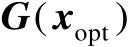 按列分块表示为
按列分块表示为
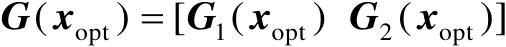 ,其中
,其中
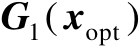 为
为
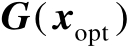 的前
的前
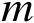 列构成的子矩阵(可逆),
列构成的子矩阵(可逆),
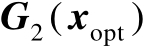 为
为
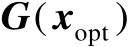 的后
的后
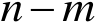 列构成的子矩阵,则在向量
列构成的子矩阵,则在向量
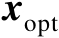 处通过对恒等式
处通过对恒等式
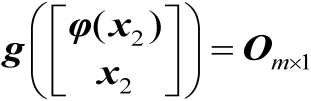 求一阶导数可以建立如下等式:
求一阶导数可以建立如下等式:
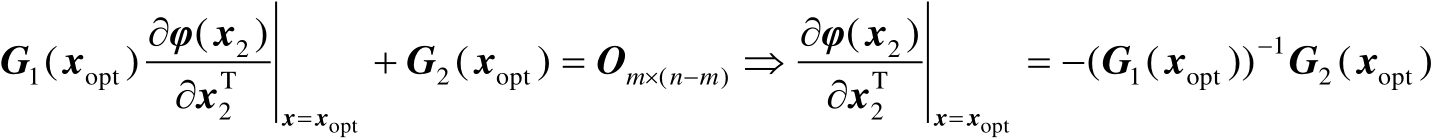
(2.53)
接着将向量
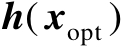 按行分块表示为
按行分块表示为
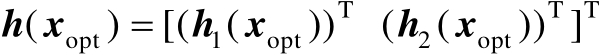 。其中,
。其中,
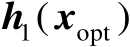 为
为
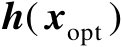 的前
的前
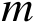 个分量构成的子向量,
个分量构成的子向量,
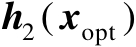 为
为
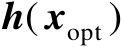 的后
的后
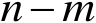 个分量构成的子向量。由于向量
个分量构成的子向量。由于向量
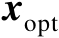 是式(2.51)的局部最优解,于是有
是式(2.51)的局部最优解,于是有
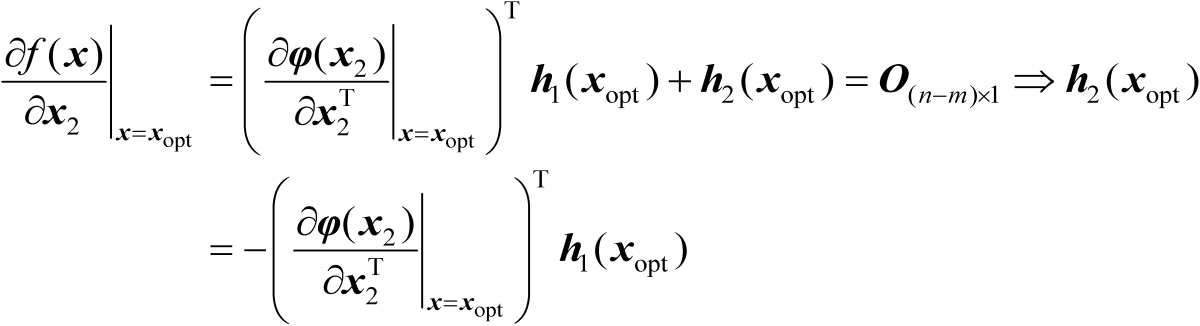
(2.54)
将式(2.53)代入式(2.54)中可得
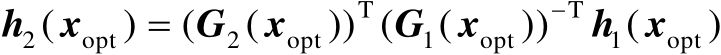
(2.55)
若令
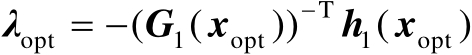 ,则有
,则有
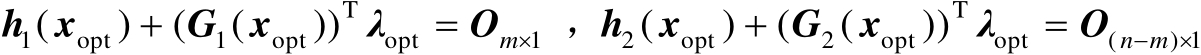
(2.56)
将式(2.56)中的两个等式合并可得
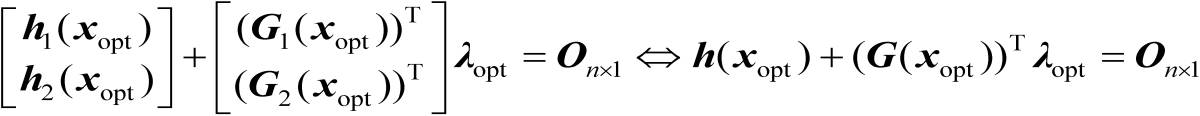
(2.57)
证毕。
命题2.14间接给出了求解式(2.51)的方法,即拉格朗日乘子法。为了求解式(2.51)可以构造如下拉格朗日函数:
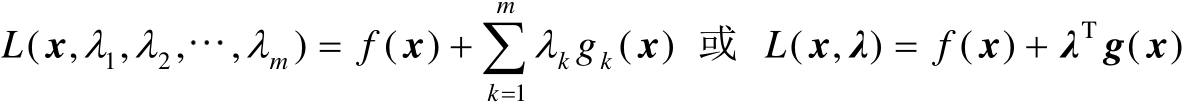
(2.58)
式中,
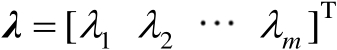 称为拉格朗日乘子。式(2.51)的最优解
称为拉格朗日乘子。式(2.51)的最优解
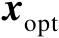 和
和
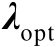 需要满足如下等式:
需要满足如下等式:
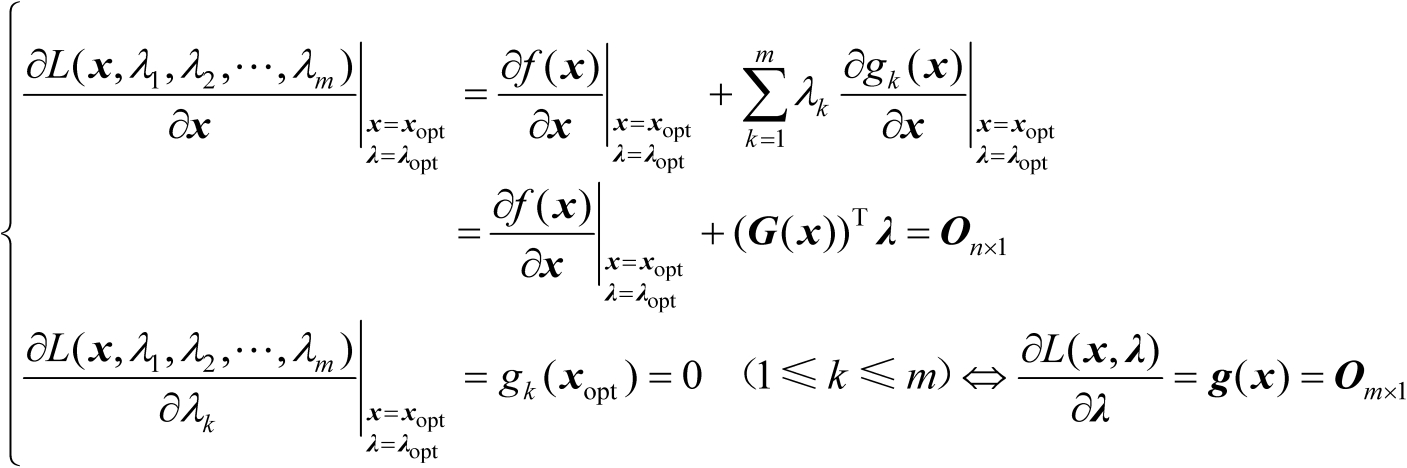
(2.59)
可以将式(2.59)看成关于
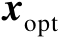 和
和
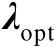 的方程组,其中的方程个数为
的方程组,其中的方程个数为
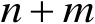 ,未知参数个数也为
,未知参数个数也为
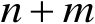 。在一些特殊情况下,该方程组存在闭式解,但是在绝大多数情况下,该方程组并不存在闭式解,需要通过数值技术来进行求解。
。在一些特殊情况下,该方程组存在闭式解,但是在绝大多数情况下,该方程组并不存在闭式解,需要通过数值技术来进行求解。
2.两种数学优化模型
下面将讨论本书涉及的两种数学优化模型,第1种模型存在最优闭式解,第2种模型则不存在最优闭式解。
首先考虑第1种模型。设列满秩矩阵
 、正定矩阵
、正定矩阵
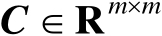 、向量
、向量
 及向量组
及向量组
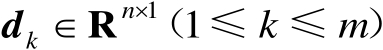 ,相应的数学优化模型为
,相应的数学优化模型为
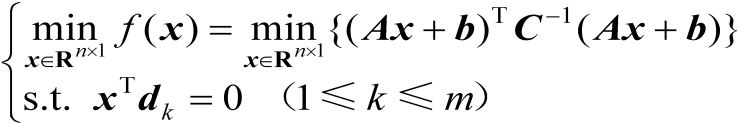
(2.60)
式(2.60)对应的拉格朗日函数为
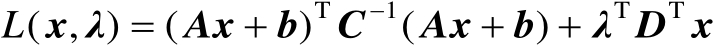
(2.61)
式中,
 ,假设其为列满秩矩阵。根据式(2.59)可知,式(2.60)的最优解
,假设其为列满秩矩阵。根据式(2.59)可知,式(2.60)的最优解
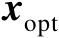 和
和
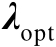 应满足如下等式:
应满足如下等式:
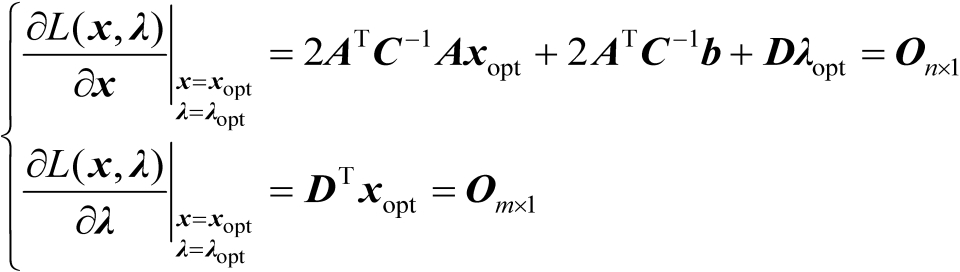
(2.62)
由式(2.62)中的第1式可得
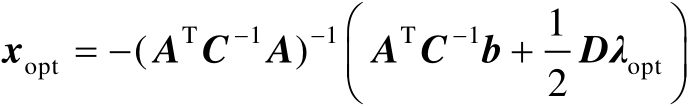
(2.63)
将式(2.63)代入式(2.62)中的第2式可得
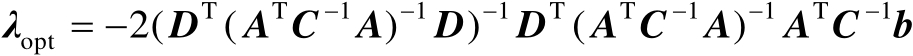
(2.64)
最后将式(2.64)代入式(2.63)中可得
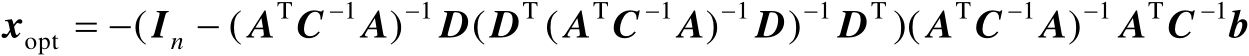
(2.65)
从上述推导中不难发现,优化模型式(2.60)的最优闭式解存在,这是因为其中的等式约束为线性约束。
接着考虑第2种模型。设列满秩矩阵
 、正定矩阵
、正定矩阵
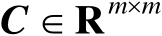 、向量
、向量
 、向量组
、向量组
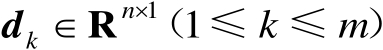 、对称矩阵组
、对称矩阵组
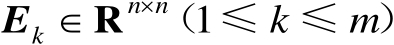 及标量组
及标量组
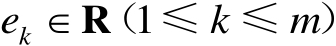 ,相应的数学优化模型为
,相应的数学优化模型为
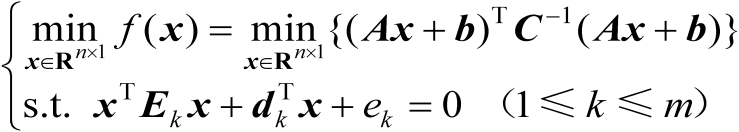
(2.66)
式(2.66)对应的拉格朗日函数为
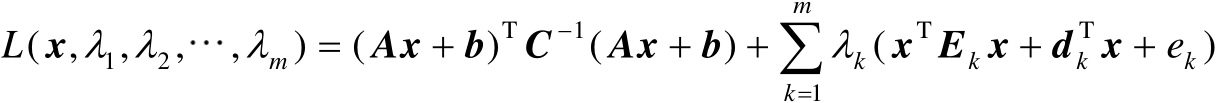
(2.67)
根据式(2.59)可知,式(2.66)的最优解
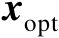 和
和
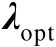 应满足如下等式:
应满足如下等式:
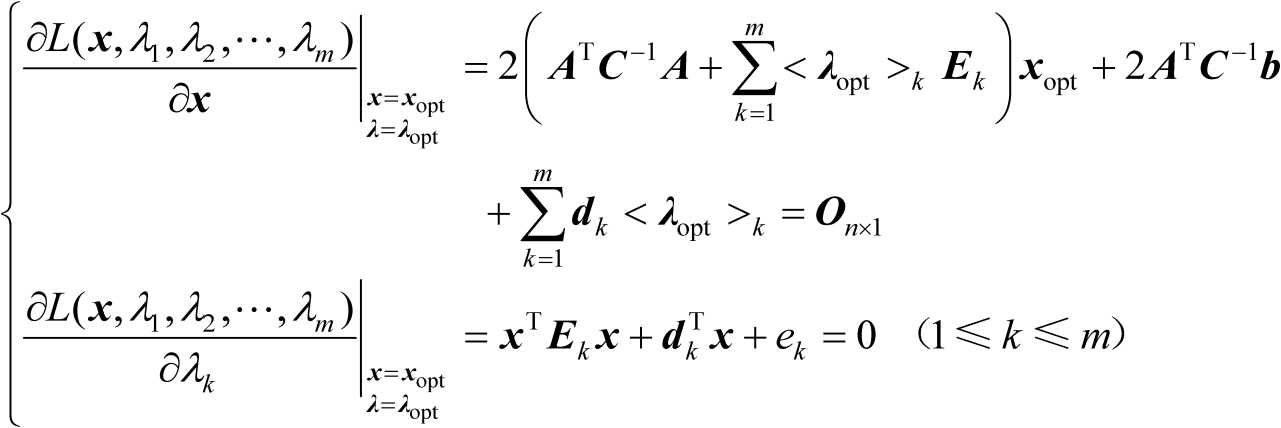
(2.68)
由式(2.68)中的第1式可得
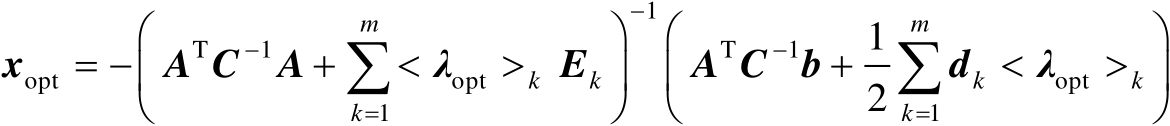
(2.69)
将式(2.69)代入式(2.68)中的第2式可得
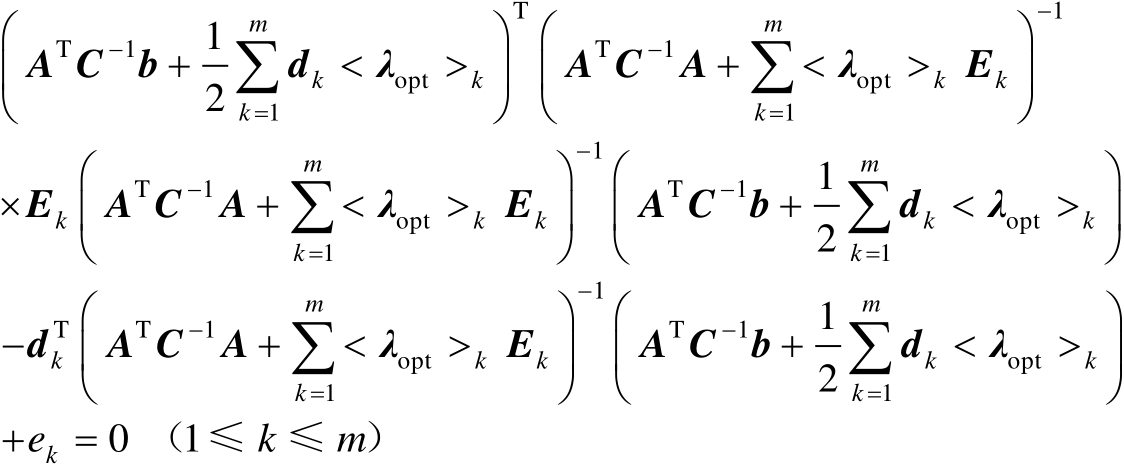
(2.70)
不难发现,式(2.70)是关于
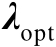 的非线性方程,需要通过迭代或多项式求根的方式进行数值求解,将
的非线性方程,需要通过迭代或多项式求根的方式进行数值求解,将
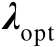 的数值解代入式(2.69)中即可得到最优解
的数值解代入式(2.69)中即可得到最优解
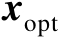 。从上述推导中不难发现,由于
。从上述推导中不难发现,由于
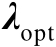 的最优闭式解并不存在,因此优化模型式(2.66)的最优闭式解无法获得,需要利用数值技术进行求解,这是因为其中的等式约束为非线性约束(事实上为二次约束)。
的最优闭式解并不存在,因此优化模型式(2.66)的最优闭式解无法获得,需要利用数值技术进行求解,这是因为其中的等式约束为非线性约束(事实上为二次约束)。