




本节将介绍关于矩阵理论的预备知识,其中涉及矩阵求逆计算公式、Moore-Penrose广义逆矩阵和正交投影矩阵、矩阵Kronecker积和矩阵向量化运算、矩阵奇异值分解、一个重要的矩阵等式,以及标量函数的梯度向量和向量函数的Jacobian矩阵。
下面将介绍几个重要的矩阵求逆公式。
1.矩阵和求逆公式
【命题2.1】
设矩阵
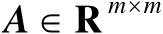 、
、
 、
、
 及
及
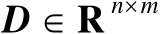 ,并且矩阵
,并且矩阵
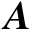 、
、
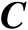 及
及
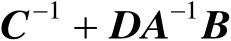 均可逆,则有如下等式:
均可逆,则有如下等式:
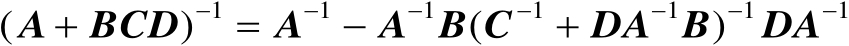
(2.1)
【证明】 根据矩阵乘法运算法则可知
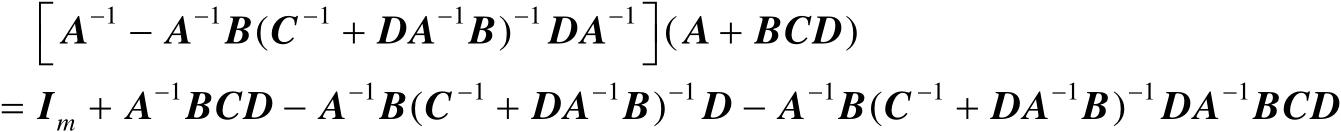
(2.2)
将矩阵
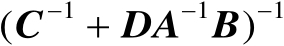 表示为
表示为
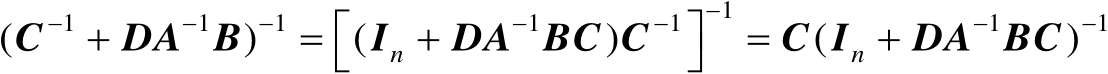
(2.3)
将式(2.3)代入式(2.2)中可得
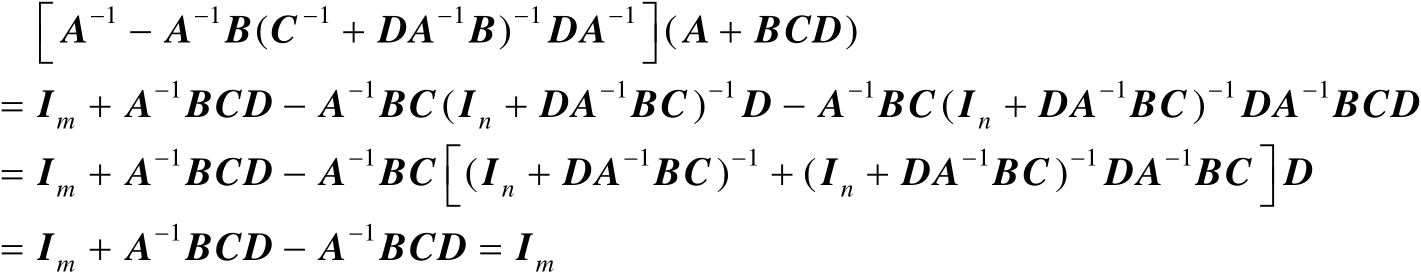
(2.4)
由式(2.4)可知式(2.1)成立。证毕。
【命题2.2】
设矩阵
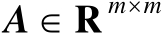 、
、
 、
、
 及
及
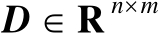 ,并且矩阵
,并且矩阵
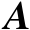 、
、
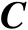 及
及
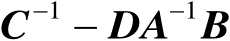 均可逆,则有如下等式:
均可逆,则有如下等式:
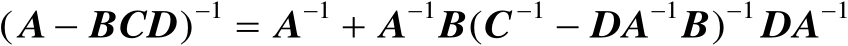
(2.5)
【证明】
将式(2.1)中的矩阵
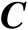 替换为
替换为
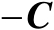 即可知式(2.5)成立。证明过程略。
即可知式(2.5)成立。证明过程略。
2.分块对称矩阵求逆公式
【命题2.3】 设有如下分块对称可逆矩阵:
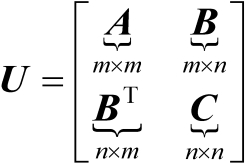
(2.6)
其中,
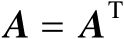 和
和
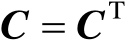 ,并且矩阵
,并且矩阵
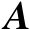 、
、
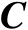 、
、
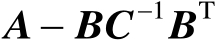 及
及
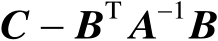 均可逆,则有如下等式:
均可逆,则有如下等式:
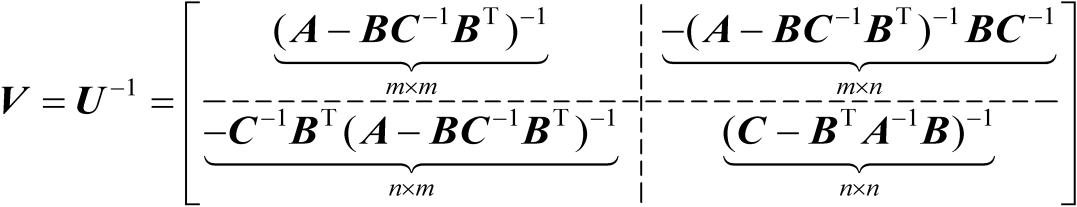
(2.7)
【证明】
首先将矩阵
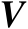 表示成如下分块形式:
表示成如下分块形式:
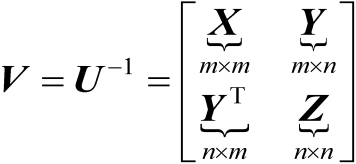
(2.8)
根据逆矩阵的定义可得
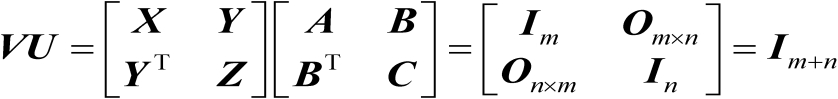
(2.9)
基于式(2.9)可以得到如下3个等式:
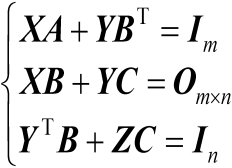
(2.10)
利用式(2.10)中的第2式可知
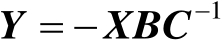 ,将其代入式(2.10)中的第1式可得
,将其代入式(2.10)中的第1式可得
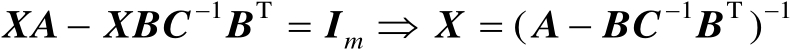
(2.11)
由式(2.11)可知
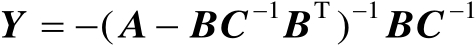
(2.12)
结合式(2.10)中的第3式和式(2.12)可得
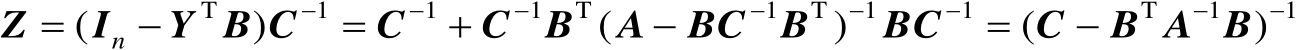
(2.13)
式中,第3个等号处的运算利用了命题2.2。结合式(2.11)~式(2.13)可知式(2.7)成立。证毕。
下面将介绍关于Moore-Penrose广义逆矩阵和正交投影矩阵的若干重要结论。
1.Moore-Penrose广义逆矩阵
Moore-Penrose广义逆矩阵是一种十分重要的广义逆矩阵,利用该逆矩阵可以构造任意矩阵的列空间或是其列补空间上的正交投影矩阵,其基本定义如下。
【定义2.1】
设矩阵
 ,若矩阵
,若矩阵
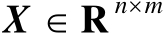 满足以下4个矩阵方程:
满足以下4个矩阵方程:
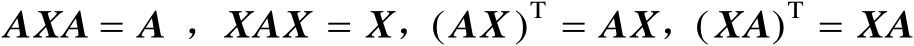
(2.14)
则称
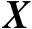 是矩阵
是矩阵
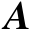 的Moore-Penrose广义逆矩阵,并将其记为
的Moore-Penrose广义逆矩阵,并将其记为
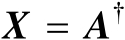 。
。
根据定义2.1可知,若
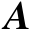 是可逆方阵,则有
是可逆方阵,则有
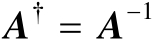 。满足式(2.14)的Moore-Penrose逆矩阵存在并且唯一,它可以通过矩阵
。满足式(2.14)的Moore-Penrose逆矩阵存在并且唯一,它可以通过矩阵
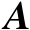 的奇异值分解来获得
[50,51]
。对于列满秩矩阵或行满秩矩阵而言,Moore-Penrose逆矩阵存在闭式表达式,具体可见如下两个命题。
的奇异值分解来获得
[50,51]
。对于列满秩矩阵或行满秩矩阵而言,Moore-Penrose逆矩阵存在闭式表达式,具体可见如下两个命题。
【命题2.4】
设矩阵
 ,若为列满秩矩阵,则有
,若为列满秩矩阵,则有
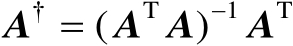 。
。
【证明】
若
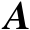 为列满秩矩阵,则
为列满秩矩阵,则
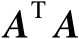 是可逆矩阵,现将
是可逆矩阵,现将
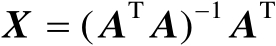 代入式(2.14)中可得
代入式(2.14)中可得
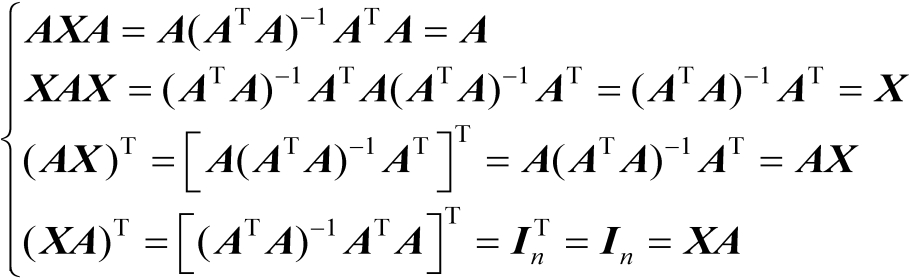
(2.15)
由式(2.15)可知,矩阵
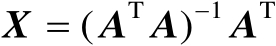 满足Moore-Penrose广义逆定义中的4个矩阵方程。证毕。
满足Moore-Penrose广义逆定义中的4个矩阵方程。证毕。
【命题2.5】
设矩阵
 ,若
,若
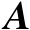 为行满秩矩阵,则有
为行满秩矩阵,则有
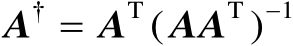 。
。
【证明】
若
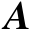 为行满秩矩阵,则
为行满秩矩阵,则
 是可逆矩阵,现将
是可逆矩阵,现将
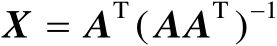 代入式(2.14)中可得
代入式(2.14)中可得
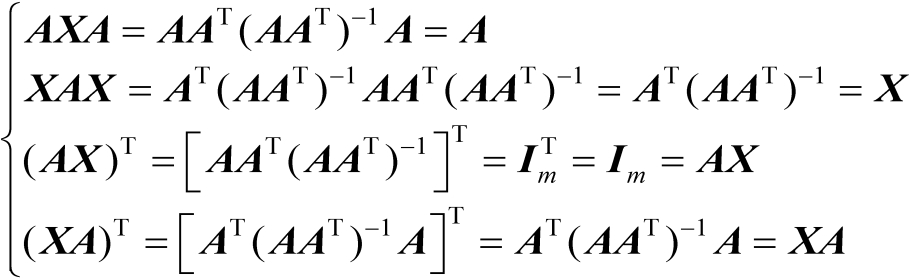
(2.16)
由式(2.16)可知,矩阵
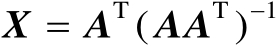 满足Moore-Penrose广义逆定义中的4个矩阵方程。证毕。
满足Moore-Penrose广义逆定义中的4个矩阵方程。证毕。
2.正交投影矩阵
正交投影矩阵在矩阵理论中具有十分重要的作用,其基本定义如下。
【定义2.2】
设
 是
是
 维欧氏空间
维欧氏空间
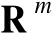 中的一个线性子空间,
中的一个线性子空间,
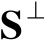 是其正交补空间,对于任意向量
是其正交补空间,对于任意向量
 ,若存在
,若存在
 阶矩阵
阶矩阵
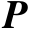 满足
满足
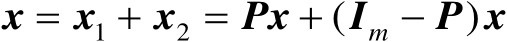
(2.17)
式中,
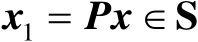 和
和
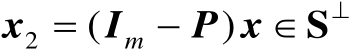 ,则称
,则称
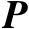 是线性子空间
是线性子空间
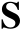 上的正交投影矩阵,
上的正交投影矩阵,
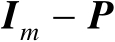 是
是
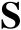 的正交补空间
的正交补空间
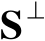 上的正交投影矩阵。若
上的正交投影矩阵。若
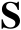 表示矩阵
表示矩阵
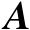 的列空间(即
的列空间(即
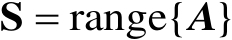 ),则将矩阵
),则将矩阵
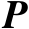 记为
记为
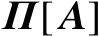 ,将矩阵
,将矩阵
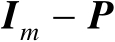 记为
记为
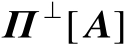 。
。
根据正交投影矩阵的定义可知,若矩阵
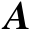 和
和
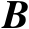 的列空间满足
的列空间满足
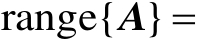
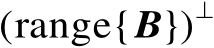 ,则有
,则有
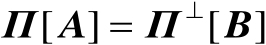 或
或
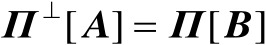 。根据正交投影矩阵的定义还可以得到如下重要结论。
。根据正交投影矩阵的定义还可以得到如下重要结论。
【命题2.6】
设
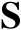 是
是
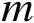 维欧氏空间
维欧氏空间
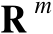 中的一个线性子空间,则该子空间上的正交投影矩阵
中的一个线性子空间,则该子空间上的正交投影矩阵
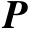 是唯一的,并且它是对称幂等矩阵,即满足
是唯一的,并且它是对称幂等矩阵,即满足
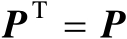 和
和
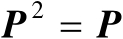 。
。
【证明】
对于任意向量
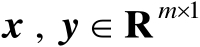 ,根据正交投影矩阵的定义可知
,根据正交投影矩阵的定义可知
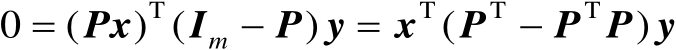
(2.18)
利用向量
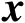 和
和
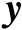 的任意性可得
的任意性可得
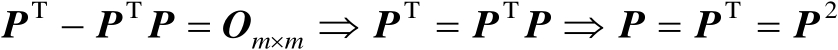
(2.19)
由式(2.19)可知,矩阵
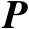 满足对称幂等性。
满足对称幂等性。
接着证明唯一性,假设存在子空间
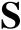 上的另一个正交投影矩阵
上的另一个正交投影矩阵
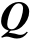 ,它也是对称幂等矩阵,则对于任意向量
,它也是对称幂等矩阵,则对于任意向量
 ,满足
,满足
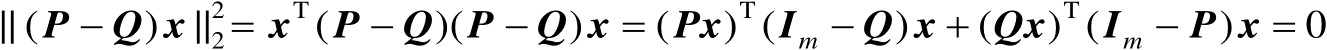
(2.20)
由向量
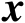 的任意性可知
的任意性可知
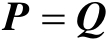 ,由此证得唯一性。证毕。
,由此证得唯一性。证毕。
【命题2.7】 任意正交投影矩阵都是半正定矩阵。
【证明】
由命题2.6可知,任意正交投影矩阵
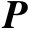 都满足
都满足
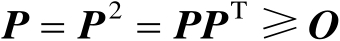 。证毕。
。证毕。
一个重要的事实是,正交投影矩阵可以利用Moore-Penrose逆矩阵来表示,具体可见如下命题。
【命题2.8】
设矩阵
 ,则其列空间和列补空间上的正交投影矩阵可以分别表示为
,则其列空间和列补空间上的正交投影矩阵可以分别表示为
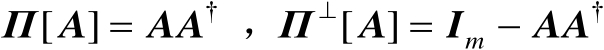
(2.21)
若
 是列满秩矩阵,则其列空间和列补空间上的正交投影矩阵还可以分别表示为
是列满秩矩阵,则其列空间和列补空间上的正交投影矩阵还可以分别表示为
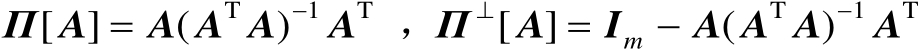
(2.22)
【证明】
任意向量
 都可以进行如下分解:
都可以进行如下分解:
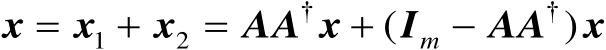
(2.23)
式中,
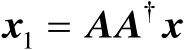 和
和
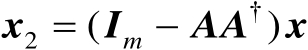 ,下面仅需要证明
,下面仅需要证明
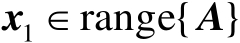 和
和
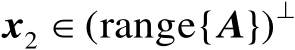 即可。首先有
即可。首先有
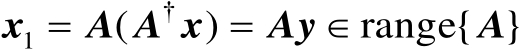
(2.24)
式中,
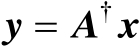 。另一方面,利用Moore-Penrose逆矩阵的性质可知
。另一方面,利用Moore-Penrose逆矩阵的性质可知
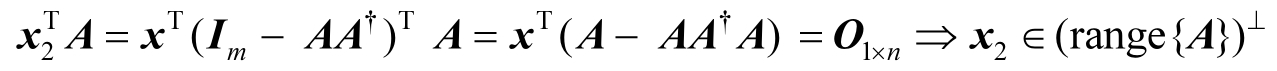
(2.25)
最后,若
 是列满秩矩阵,利用命题2.4可得
是列满秩矩阵,利用命题2.4可得
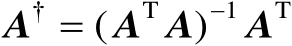 ,将该式代入式(2.21)中可知式(2.22)成立。证毕。
,将该式代入式(2.21)中可知式(2.22)成立。证毕。
下面将介绍矩阵Kronecker积和矩阵向量化运算的若干重要结论。
1.矩阵Kronecker积
矩阵Kronecker积也称为直积。设矩阵
 和
和
 ,则它们的Kronecker积可以表示为
,则它们的Kronecker积可以表示为
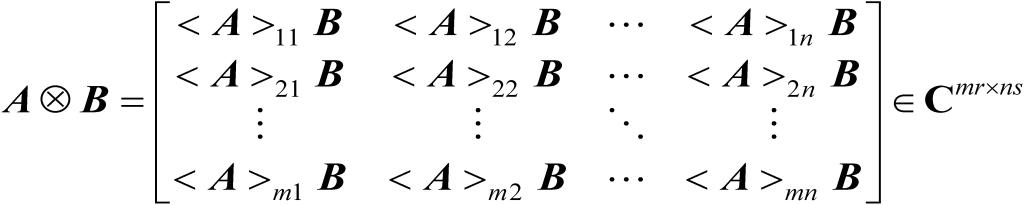
(2.26)
由式(2.26)不难看出,Kronecker积并没有交换律(即
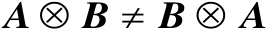 )。关于Kronecker积有如下重要结论。
)。关于Kronecker积有如下重要结论。
【命题2.9】
设矩阵
 、
、
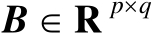 、
、
 及
及
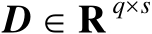 ,则有如下等式
,则有如下等式
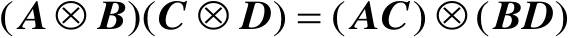
(2.27)
【证明】
将矩阵
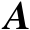 位于坐标
位于坐标
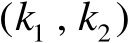 处的元素记为
处的元素记为
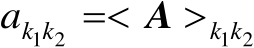 ,将矩阵
,将矩阵
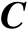 位于坐标
位于坐标
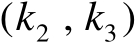 处的元素记为
处的元素记为
 ,于是矩阵
,于是矩阵
 中第
中第
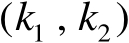 个阶数为
个阶数为
 的子矩阵为
的子矩阵为
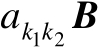 ,矩阵
,矩阵
 中第
中第
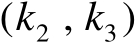 个阶数为
个阶数为
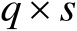 的子矩阵为
的子矩阵为
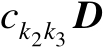 。因此,矩阵
。因此,矩阵
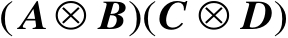 中第
中第
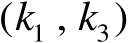 个阶数为
个阶数为
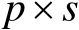 的子矩阵为
的子矩阵为
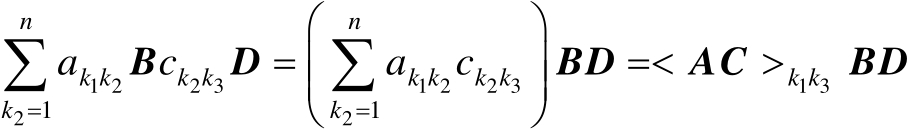
(2.28)
显然,式(2.28)右边恰好等于矩阵
 中第
中第
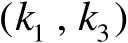 个阶数为
个阶数为
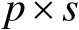 的子矩阵,由此可知式(2.27)成立。证毕。
的子矩阵,由此可知式(2.27)成立。证毕。
2.矩阵向量化运算
矩阵向量化(记为
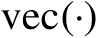 )的概念具有广泛的应用,它可以简化数学表述,基本定义如下。
)的概念具有广泛的应用,它可以简化数学表述,基本定义如下。
【定义2.3】
设矩阵
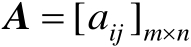 ,则该矩阵的向量化运算可定义为
,则该矩阵的向量化运算可定义为
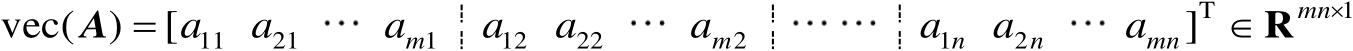
(2.29)
由式(2.29)可知,矩阵向量化是将矩阵按照字典顺序排成列向量。利用矩阵向量化运算可以得到关于Kronecker积的重要等式,具体可见如下命题。
【命题2.10】
设矩阵
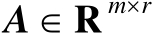 、
、
 及
及
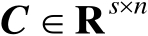 ,则有
,则有
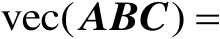
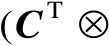
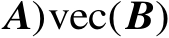 。
。
【证明】
首先将矩阵
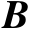 按列分块表示为
按列分块表示为
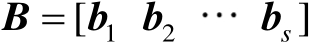 ,由此可以将矩阵
,由此可以将矩阵
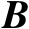 进一步表示为
进一步表示为
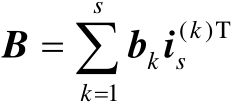
(2.30)
基于式(2.30)可得
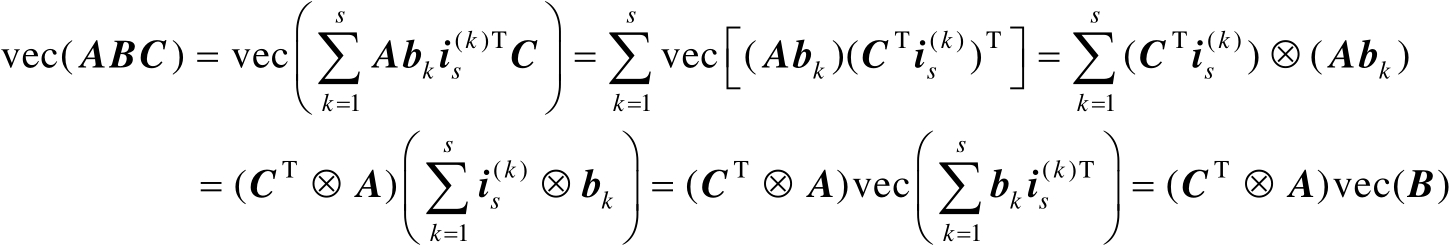
(2.31)
式中,第4个等号处的运算利用了命题2.9。证毕。
下面将介绍矩阵奇异值分解的基本概念。奇异值分解是一种非常重要的矩阵分解,通过此分解可以获得矩阵的列空间和零空间,并且还可以确定矩阵的秩。任意矩阵都存在奇异值分解,具体可见如下命题。
【命题2.11】
设矩阵
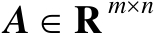 ,并且其秩为
,并且其秩为
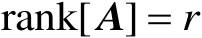 ,则存在两个正交矩阵
,则存在两个正交矩阵
 和
和
 满足
满足
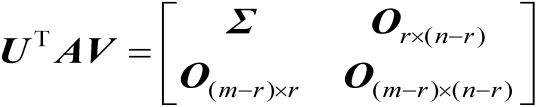
(2.32)
式中,
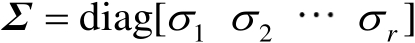 ,其中
,其中
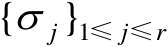 称为奇异值,矩阵
称为奇异值,矩阵
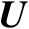 和
和
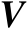 中的列向量分别称为左和右奇异向量。
中的列向量分别称为左和右奇异向量。
【证明】
由于
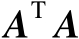 是半正定矩阵,并且其秩为
是半正定矩阵,并且其秩为
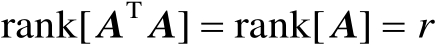 ,因此矩阵
,因此矩阵
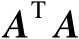 的特征值中会包含
的特征值中会包含
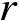 个正值和
个正值和
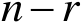 个零值,于是可以将矩阵
个零值,于是可以将矩阵
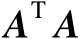 的全部特征值设为
的全部特征值设为
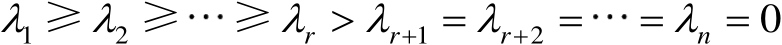
(2.33)
并记
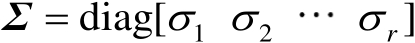 ,其中
,其中
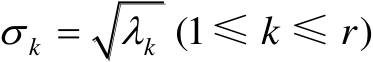 。根据对称矩阵的特征分解定理
[50,51]
可知,存在正交矩阵
。根据对称矩阵的特征分解定理
[50,51]
可知,存在正交矩阵
 满足
满足
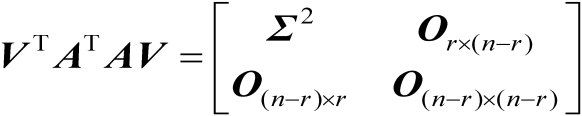
(2.34)
由式(2.34)可以进一步推得
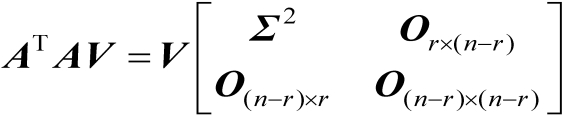
(2.35)
将矩阵
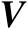 按列分块表示为
按列分块表示为
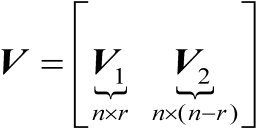 ,结合式(2.35)可知
,结合式(2.35)可知
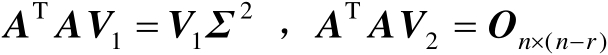
(2.36)
进一步可得
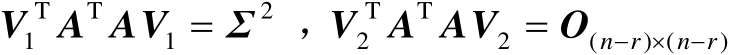
(2.37)
于是有
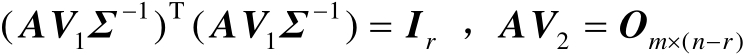
(2.38)
若令
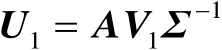 (等价于
(等价于
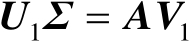 ),利用式(2.38)中的第1个等式可知,矩阵
),利用式(2.38)中的第1个等式可知,矩阵
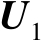 中的列向量是相互正交的单位向量,将其按列分块表示为
中的列向量是相互正交的单位向量,将其按列分块表示为
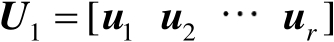 ,然后再扩充
,然后再扩充
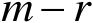 个列向量
个列向量
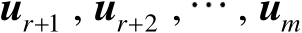 构造矩阵
构造矩阵
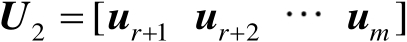 ,以使得
,以使得
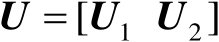 为正交矩阵。于是有
为正交矩阵。于是有
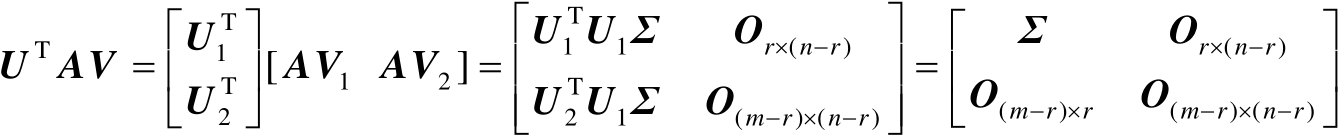
(2.39)
证毕。
根据命题2.11可知,任意矩阵
 都可以分解为如下形式:
都可以分解为如下形式:
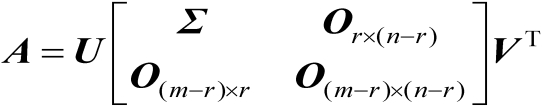
(2.40)
式中,矩阵
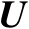 、
、
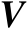 及
及
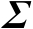 的定义见命题2.11。式(2.40)即为矩阵奇异值分解。需要指出的是,命题2.11中矩阵
的定义见命题2.11。式(2.40)即为矩阵奇异值分解。需要指出的是,命题2.11中矩阵
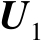 的列空间
的列空间
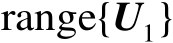 也为矩阵
也为矩阵
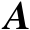 的列空间
的列空间
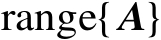 ,矩阵
,矩阵
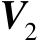 的列空间
的列空间
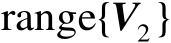 也为矩阵
也为矩阵
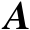 的零空间
的零空间
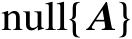 ,非零的奇异值个数
,非零的奇异值个数
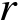 也为矩阵
也为矩阵
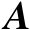 的秩
的秩
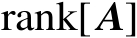 。
。
下面将证明一个重要的矩阵等式,它对于本书中的加权多维标度定位方法非常重要。
【命题2.12】
设向量组为
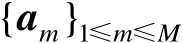 ,其中
,其中
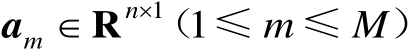 ,若令
,若令
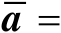
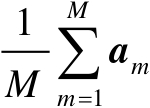 ,并定义如下两个矩阵:
,并定义如下两个矩阵:
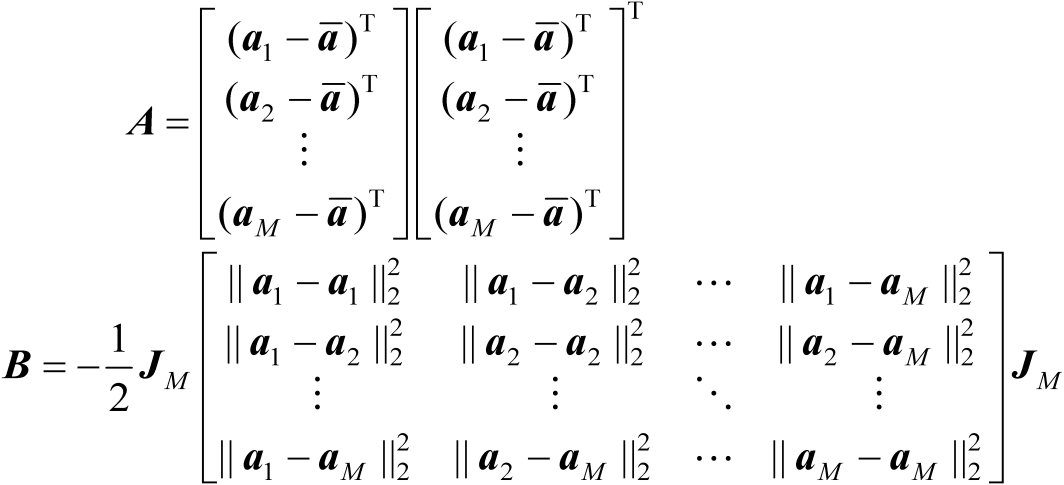
(2.41)
式中,
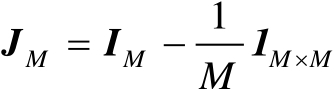 ,则有
,则有
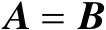 。
。
【证明】
矩阵
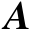 中的第
中的第
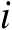 行、第
行、第
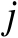 列元素为
列元素为
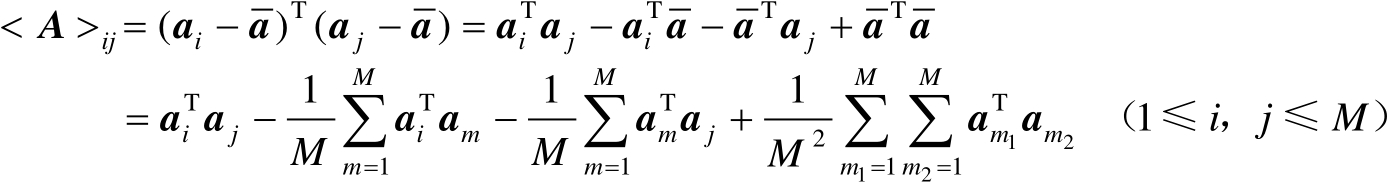
(2.42)
矩阵
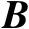 中的第
中的第
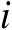 行、第
行、第
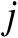 列元素为
列元素为
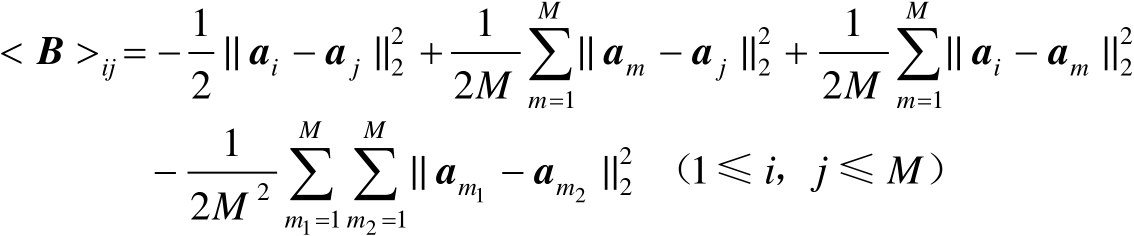
(2.43)
将式(2.43)中的2-范数进一步展开可得
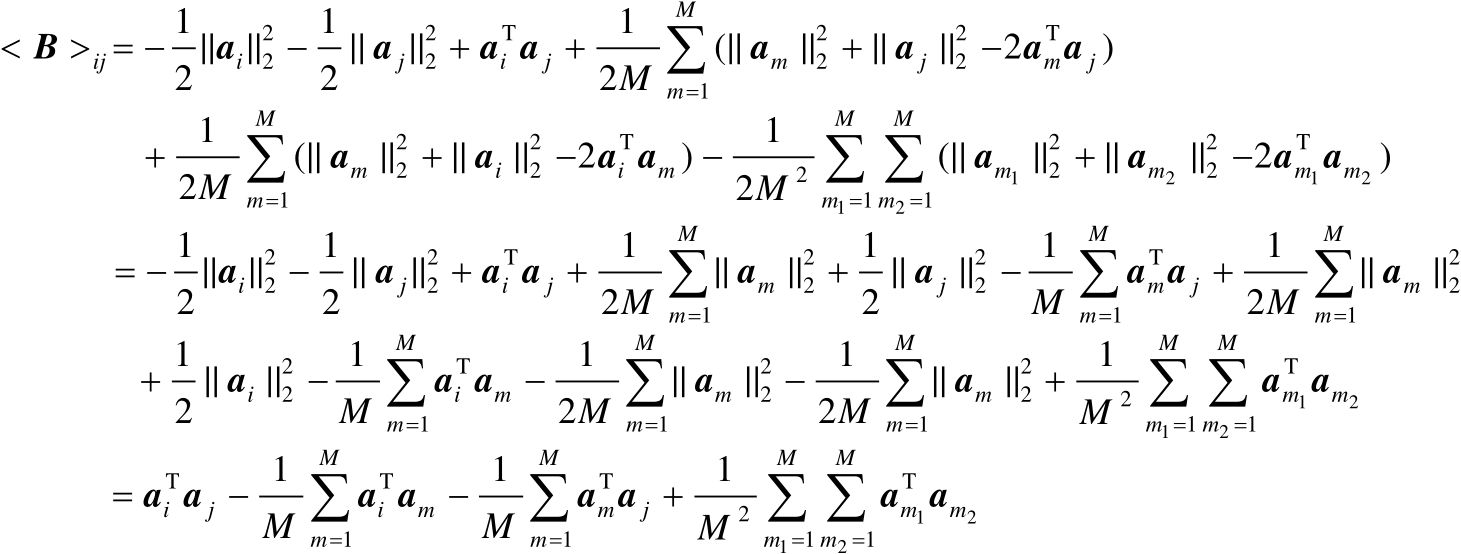
(2.44)
比较式(2.43)和式(2.44)可知
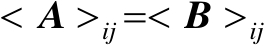 ,由此可得
,由此可得
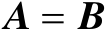 。证毕。
。证毕。
下面将介绍标量函数的梯度向量和向量函数的Jacobian矩阵的基本概念。
1.标量函数的梯度向量
【定义2.4】
设
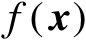 是关于
是关于
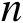 维实向量
维实向量
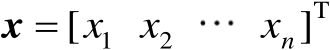 的连续且一阶可导的标量函数,则其梯度向量定义为
的连续且一阶可导的标量函数,则其梯度向量定义为
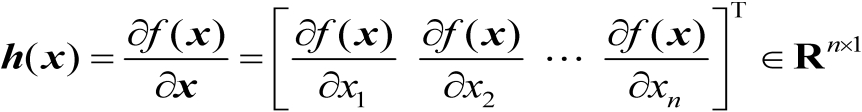
(2.45)
利用梯度向量的定义,下面将给出一个重要结论,具体可见如下命题。
【命题2.13】
设列满秩矩阵
 、正定矩阵
、正定矩阵
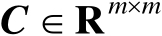 及向量
及向量
 ,则无约束优化问题
,则无约束优化问题
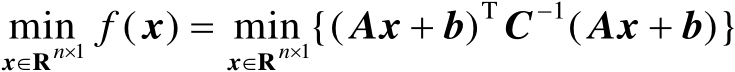
(2.46)
的唯一最优解为
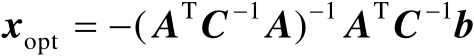
(2.47)
【证明】
首先获得标量函数
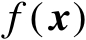 的梯度向量,如下式所示:
的梯度向量,如下式所示:
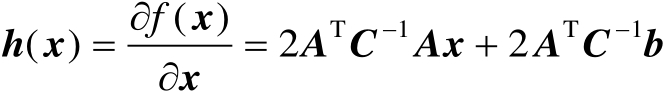
(2.48)
由于最优解
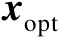 应使得梯度为零向量,于是有
应使得梯度为零向量,于是有
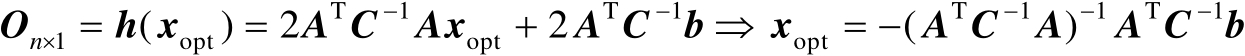
(2.49)
该最优解的唯一性是由于
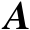 是列满秩矩阵。证毕。
是列满秩矩阵。证毕。
2.向量函数的Jacobian矩阵
【定义2.5】
设由
m
个标量函数构成的向量函数
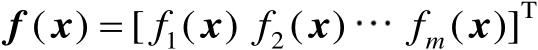 ,其中每个标量函数
,其中每个标量函数
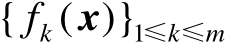 都是关于
都是关于
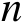 维实向量
维实向量
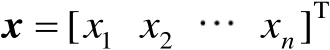 的连续且一阶可导函数,则其Jacobian矩阵定义为
的连续且一阶可导函数,则其Jacobian矩阵定义为
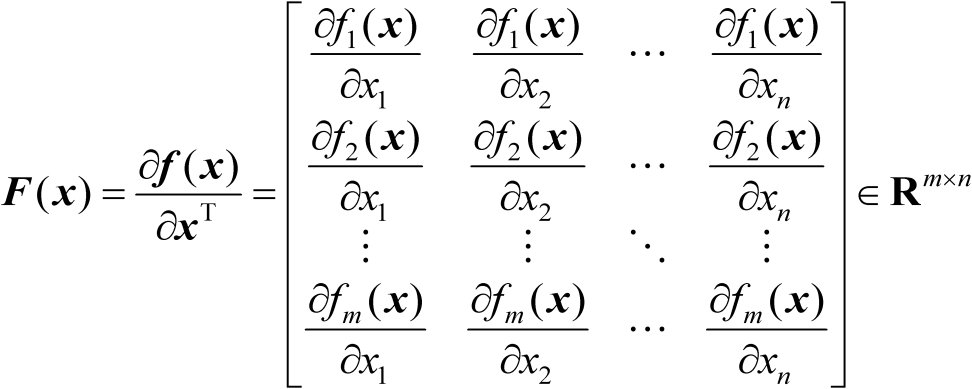
(2.50)
比较式(2.45)和式(2.50)可知,Jacobian矩阵
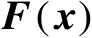 中的第
中的第
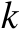 行向量是标量函数
行向量是标量函数
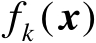 的梯度向量的转置。
的梯度向量的转置。