





混沌是一种貌似无规则的运动,是指在确定非线性系统中,不需要附加任何随机因素就可以实现的类随机行为。混沌系统最大的特点在于系统对演化初始条件极度敏感,从长期意义上讲,系统的未来行为是不可预测的 [4] 。它的定常状态不属于通常概念下确定性运动的3种状态,即静止、周期运动和准周期运动,而是一种始终局限于有限区域且轨道永不重复、状态复杂的运动。
由于混沌系统的奇异性和复杂性至今还没有被人们彻底了解,因此,到目前为止还没有形成有关混沌的统一定义,已有的定义仅能从不同的侧面来反映混沌的性质。在众多的定义中,被学术界广泛认可的是李天岩和J. Yorke(Li-Yorke)对混沌的定义,1975年,他们在 Period Three Implies Chaos 一文中给出了混沌的一种数学定义,它是从区间映射出发进行定义的。该定义的描述如下 [2] 。
定义1.1 Li-Yorke的混沌定义 闭区间Ⅰ上的连续自映射 f ( x ),如果满足下面的条件,便可确定它有混沌现象。
(1) f 的周期点是周期无上界的。
(2)闭区间Ⅰ上存在不可数子集 S ,满足:
①对任意
x
,
y
∈
S
,当
x
≠
y
时,
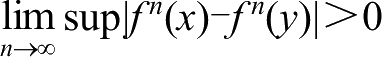 。
。
②对任意
x
,
y
∈
S
,
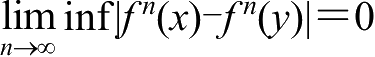 。
。
③对任意
x
∈
S
和
f
的任意周期点
y
,
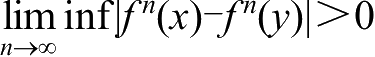 。
。
这里,sup| f n ( x )- f n ( y )|和inf| f n ( x )- f n ( y )|分别表示 f n ( x )与 f n ( y )的距离的上确界和下确界。
定理1.1 Li-Yorke定理 设 f ( x )是闭区间Ⅰ上的[ a , b ]连续自映射,若 f ( x )有3个周期点,则对任何正整数 n , f ( x )有 n 个周期点。
在此定义中,由于前两个极限说明子集的点 X 1 、 X 2 相当分散而又相当集中,第3个极限说明子集不会趋近于任意周期点,所以这个定理本身只预言了有非周期轨道存在,既不涉及这些非周期点的集合是否具有非零测度,也不涉及哪个周期是稳定的。
定义1.2 Devaney的混沌定义 在拓扑意义下,混沌的定义为:设 V 是一个度量空间,映射 f ∶ V → V ,如果满足下面3个条件,则称 f 在 V 上是混沌的。
(1)对初始条件的敏感性:存在 σ >0,对于任意的 ε >0和任意的 x ∈ V ,在 x 的 ε 邻域内存在 y 和自然数 n ,使 d ( f n ( x ), f n ( y ))> σ 。
(2)拓扑传递性:对于 V 上的任意一对开集 Z , y ∈ V ,存在 k >0,使 f n ( Z )∩ Y =Ø。
(3)周期点集的稠密性: y 的周期点集在 V 中稠密。
从稳定的角度考虑,混沌轨道是局部不稳定的,“对初始条件的敏感性”就是对混沌轨道的这种不确定性的描述。对于初值敏感依赖性,意味着无论 x 、 y 离得多么近,在 f 的作用下,两者的轨道都可能分开较大的距离;而且在每个点 x 附近都可以找到距离它很近,而在 f 的作用下最终分道扬镳的点 y 。对于这样的 f ,如果用计算机计算它的轨道,任何微小的初始误差,经过若干次迭代后都将导致计算结果的失败。拓扑传递意味着任意一点的邻域在 f 的作用下,将遍历整个度量空间,这说明不可能细分或不能分解为两个不互相影响的子系统。
前面两个条件一般来说是随机系统的特征,但第3个条件“周期点集的稠密性”却又表明系统具有很强的确定性和规律性,绝非一片混乱,而是形似紊乱实则有序,这也是混沌能够和其他应用学科相结合走向实际应用的前提。
在特定条件下,可以验证Devaney的混沌定义强于Li-Yorke的混沌定义。此外,还有如Smale马蹄、横截同宿点、拓扑混合及符号动力系统等相关定义。
混沌现象是人们从自然界中发现的一大类普遍现象,存在于人们生活的方方面面,如自然界中的龙卷风、地震、地壳运动、天气变化、洋流、海岸线分布特征等,社会经济现象中的股票变化趋势、疾病发病趋势、人口分布及增长规律等。由此可见,混沌现象是一种十分常见的自然和社会现象,正是由于其太过普遍,往往被人们忽视。混沌现象蕴含的自然规律是十分丰富和富有研究价值的,在纷繁复杂的现象背后,混沌现象又有某种可以总结的共同本质属性。
混沌是确定性非线性动力学系统中对初始条件具有敏感性的非周期有界动态行为。混沌运动是在确定性系统中出现的类随机过程。混沌运动具有确定性运动所没有的本质特征,具体体现在几何和统计方面包括有界性、遍历性、对初始条件的敏感性、伪随机性特征、奇异吸引子、分维性及Lyapunov指数等 [5] 。下面将具体分析混沌的主要特征。
混沌是有界的,其运动轨道始终局限于一个确定的区域内,该区域被称为混沌吸引域。无论混沌系统内部多么不稳定,它的轨道都不会走出混沌吸引域,所以从整体上说混沌系统是稳定的。
混沌运动轨道局限于一个确定的区域——混沌吸引域,混沌运动在其吸引域内是各态遍历的,混沌轨道经过吸引域内的每个状态点。
由于混沌系统的Lyapunov指数大于0,因此相邻的轨道间存在指数分离现象。这种指数分离现象会导致初始条件中很小的测量误差迅速扩大,使得动力系统完全失去长期预测能力。
(1)时域随机现象。不同于常见的周期运动,混沌运动在表面上总是呈现出随机混乱的现象,它虽然不是以固定的周期经过某些状态,但是也并不发散,而是不定期地无限接近相空间上的各状态。
(2)自相关特性。混沌序列的自相关性会随着相关距离的增加而迅速衰减,呈现出与随机信号相似的特性。
例1.1 连续Logistic映射系统的时域随机性、初值敏感性和自相关特性。
混沌运动在时域上表现为随机运动现象,以著名的Logistic混沌映射为例,该映射在 μ >3.56995时处于混沌运动状态。当参数 μ 取值为3.89时,其映射函数可表示为
x n -1 =3.89 x n (1- x n ) (1.1)
图1.1为初值 x 0 =0.345501的时域图,从图中可以看到,混沌在时域上表现为一种非周期的运动,这种非周期性可以看作一种伪随机运动。
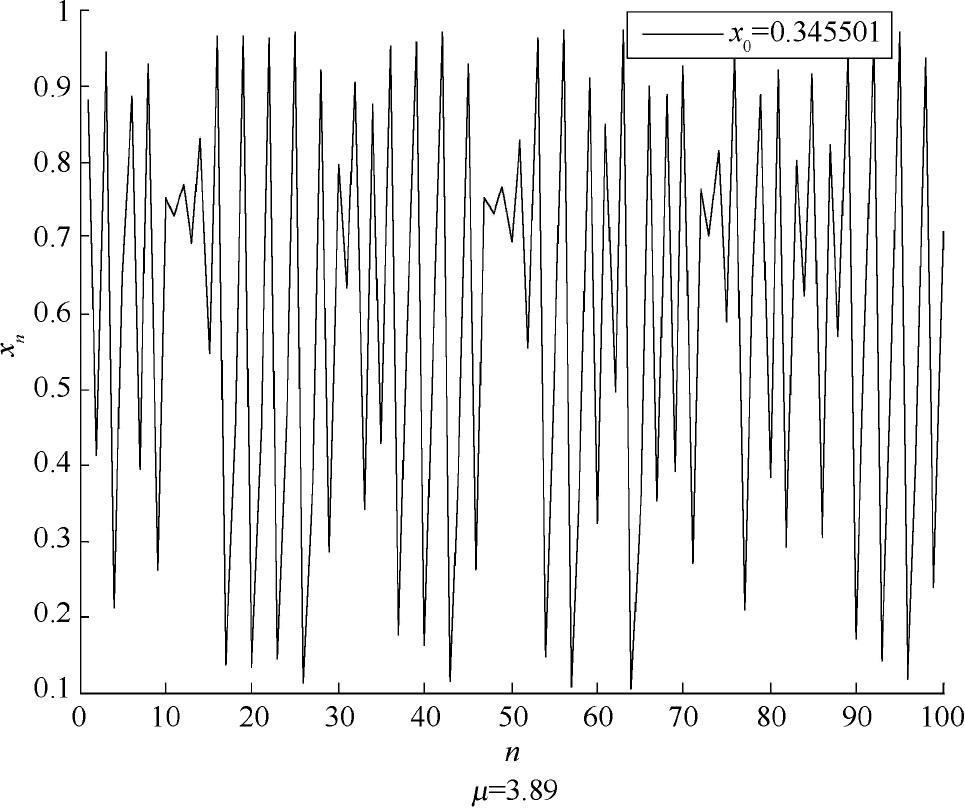
图1.1 Logistic映射的时域图
图1.2为在 x 0 =0.345500和 x 0 =0.345501条件下,Logistic映射的时域图,从图中可以看出,两条初始状态相位差为10 -6 的Logistic映射轨道迭代约30次后,在相空间中完全分离,轨道的初始信息随着动力系统的演化迅速丢失,造成混沌系统的长期不可预测。
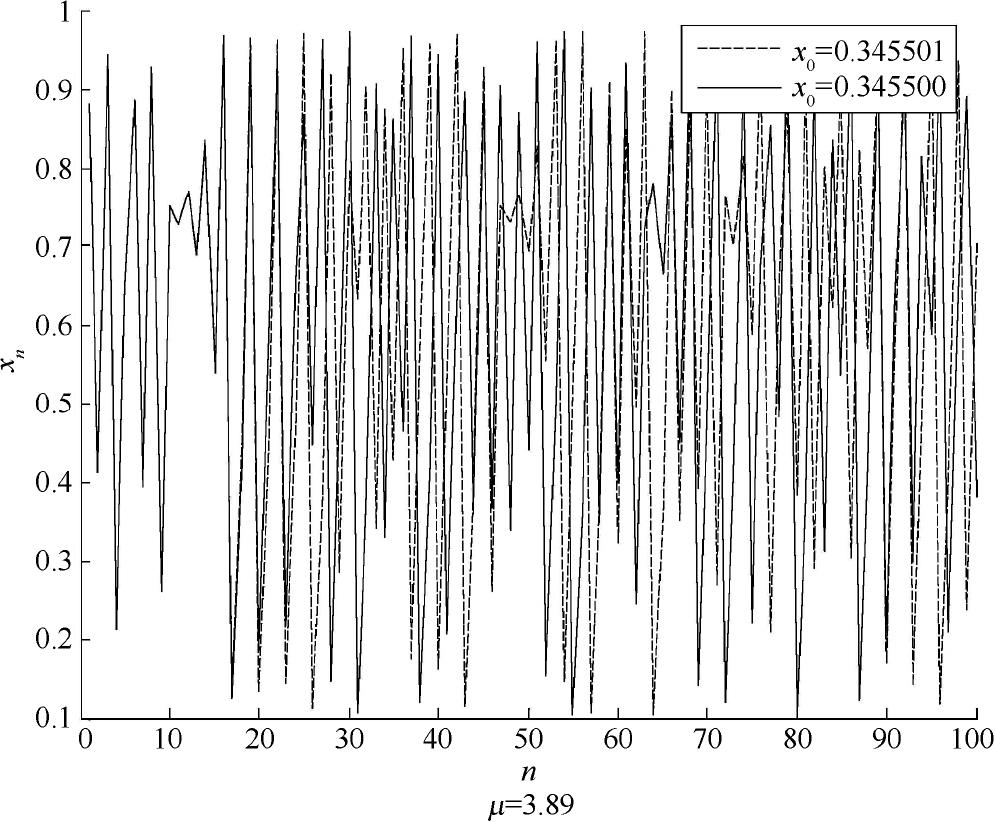
图1.2 不同初值映射轨道分离
将初值 x 0 =0.345500分别迭代6000次,计算其自相关特性,得到的自相关特性如图1.3所示。从图中可以看出,混沌信号的这一特性与随机信号的特性极为相似,因此很难用常规的线性统计分析方法进行有效分析。混沌映射迭代值的这种特性,特别适用于加密技术和跳频通信技术。
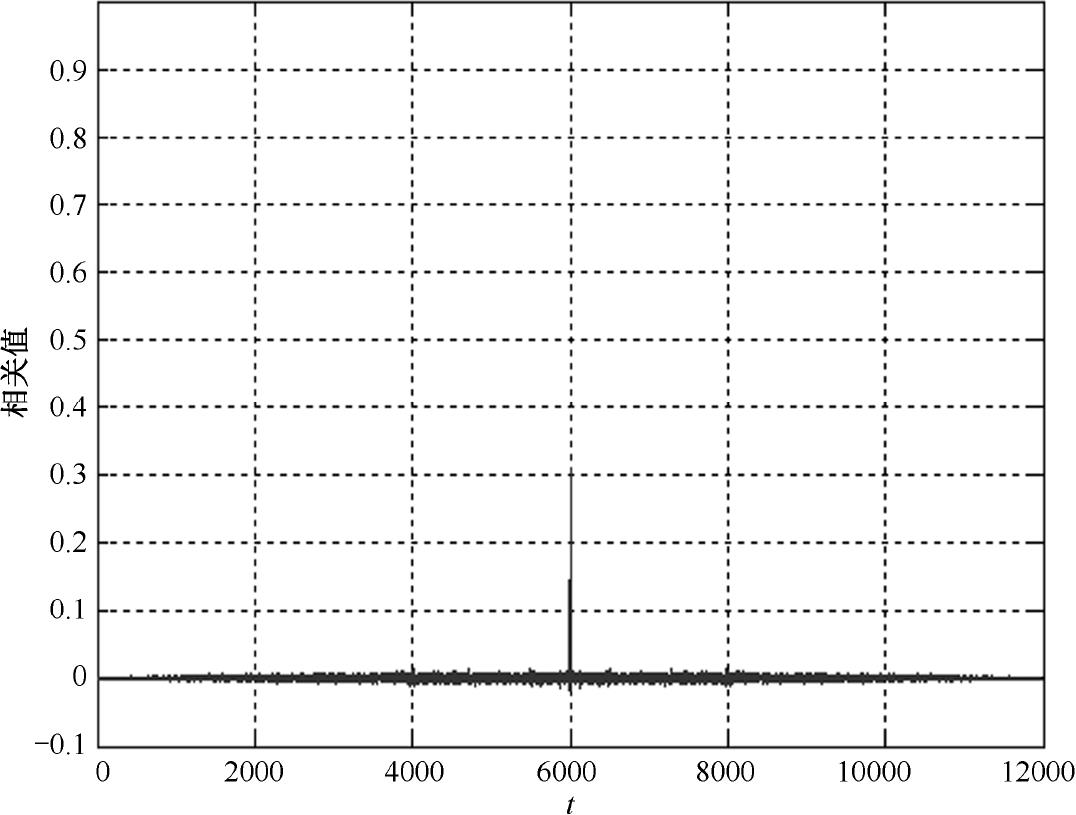
图1.3 Logistic映射的自相关特性
混沌系统除具有上述4个典型的特征外,还具有分维性、标度性、不变分布、嵌入维数及测度熵等特征。如何快速、准确地计算混沌系统的特征量,是混沌信号处理(CPS)领域一个重要的课题 [6] 。混沌保密通信是混沌理论与通信技术相结合的产物,其研究工作既包含属于混沌系统理论研究的内容,如重构混沌系统的相空间、混沌时间序列预测、计算奇异吸引子的Lyapunov指数和分维数、混沌系统的不变概率分布等;也包含直接服务于应用的内容,如混沌信号非线性降噪 [7] 、应用混沌理论建立非线性模型用于非线性时间序列预测和信号提取 [8] 、混沌通信系统的信道均衡技术 [9] 、混沌雷达 [10] 、混沌对抗 [11, 12] 、混沌控制与同步 [13-16] 、混沌密码 [17-23] 及各类工程领域中的混沌技术等,两者相辅相成。