下载掌阅APP，畅读海量书库
立即打开
近年来，应用混沌映射及其复合映射构造伪随机数发生器（CPRNG）是混沌保密通信理论研究的热点 [119-122] 。文献[123]的研究表明，当混沌映射及其输出函数满足特定的约束时，混沌轨道的粗粒化输出序列将成为严格的马尔可夫随机信息源，基于粗粒化过程构造的伪随机数发生器在理论上具有很高的安全性。
定义3.1 定义一个时间离散混沌动力学系统，其构造信息源的典型形式为
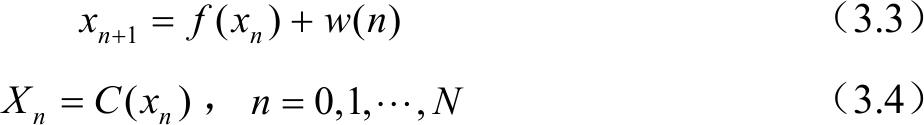
式中，{ x n }为混沌动力学系统的迭代轨迹； f ∶ S → S ， S ∈ R n 为混沌映射机制； w ( n )为噪声干扰。如无特殊说明，则认为 w ( n )为零， C ( )为定义在{0, 1, …, N }上的粗粒化输出函数，函数的输出{ X n }为 n 元序列。Kohda等人 [113, 114] 针对一维混沌系统，通过对混沌映射和输出函数施加约束，得到由混沌映射构造同分布离散无记忆信息源的一个充分条件。
定理3.1 混沌构造随机数发生器的充分条件。
对于式（3.3）和式（3.4）的混沌动力学系统和输出函数，如果它们满足下面3个条件，则生成的符号序列{ X n }为同分布离散无记忆信息源。
f
∶
S
→
S
是在区间[
a
,
b
]上的单混沌分段映射方程，即存在
S
的一个划分：
a
=
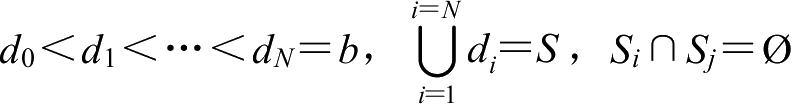，且使得对于任意
i
=1, 2, …,
N
（
i
≥2），存在
f
在自区间
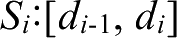上限定的映射
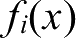为二次可微函数，满足
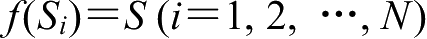，且
f
具有唯一的连续不变测度，记为
μ
(
x
)d
x
。
f 满足等概率分布特性，即
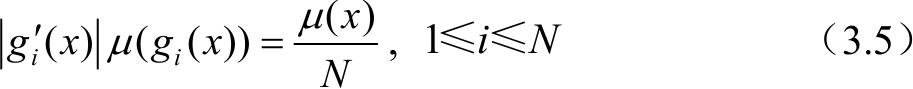
式中，
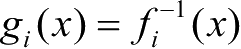为
x
的第
i
个原象。
输出函数 C ( )满足恒和属性，即
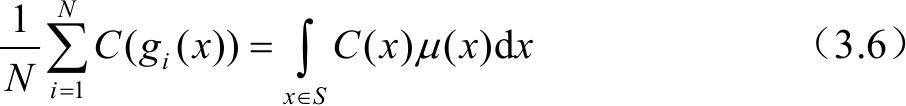
如果再添加一个约束，即
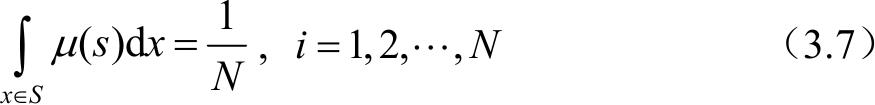
则序列 X ( n )为一个 M 进制的伪随机序列发生器。
近些年，讨论伪随机序列发生器设计方法的文献屡见不鲜 [113-118] ，其中常用的伪随机序列发生器包括线性同余发生器 [113] 、基于数论的伪随机发生器 [113, 114] 、基于线性（非线性）反馈移位寄存器的伪随机序列发生器 [113, 115] 和混沌系统伪随机序列发生器 [115-118] 。
线性同余算法是到目前为止使用最为广泛的算法，此发生器利用数论中的同余运算产生[0, 1)区间的均匀随机序列。其优点是速度快，计算每位只需要很少的操作；缺点是除算法的初始值选取具有随机性外，算法本身不具备随机性。如果攻击者破译正在使用的线性同余算法并知道算法相关参数，那么一旦获得数列中的一个数，就可以破译后续的所有数。
基于 n 级线性反馈移位寄存器（ n -LFSR）的伪随机序列发生器输出序列的性质完全由其反馈函数决定，其本身即是适宜的伪随机序列发生器，能够应用于密码学领域，在加密算法中常被用来作为构造模板。但LFSR的时序位都是线性的，也就是具有非随机特性。一个 n 位长的LFSR生成的前 n bit就是LFSR的内部初始状态，如果检测到LFSR输出连续的2 n bit，就能破译LFSR反馈多项式。通过LFSR产生的序列具有很高的相关性，对于某些应用类型，它完全不随机。
与上述两种发生器相比，基于数论的伪随机（Blum-Blurn-Shub，BBS）发生器已经被证明是密码强度较高的伪随机数发生器，文献[113]已给出了相关证明。但是，BBS发生器的安全性是基于大整数分解的困难性，尽管它是密码学上安全的伪随机比特发生器，但是如何进行大整数分解仍是其应用中亟待解决的问题，这也阻碍了BBS发生器的实际应用。
将混沌系统作为伪随机序列发生器，是近年来混沌理论研究的一个重要方向，在混沌密码学和混沌扩频领域开始崭露头角。混沌运动系统具有其他确定性运动所没有的本质特征，这些特征除了满足伪随机序列的3条公设，还完全符合加密密钥和跳频序列发生器对序列相关性、长周期、大的线性复杂度及序列数量多的要求。利用混沌系统，既可以产生数量众多、非相关、类似噪声，又可以再生的混沌序列，这种序列难以重构和预测，分析者难以破译。