3.2　序列随机性公设

序列的随机特性表现为序列的不可预测性，这就要求对序列的伪随机特性建立一套定量的度量方法，格伦布首先人为序列随机特性提出3条公设 [112] ，后被普遍认为可以作为衡量序列伪随机特性优劣的标准。

设 a 是GF( q )上周期为 q n -1 的序列，格伦布的3条公设如下。

1. 平衡特性

GF( q )中的每个非零元素在序列 a 的一个周期中恰好出现 q n -1 次；GF( q )中的零元素在序列 a 的一个周期中恰好出现 q n -1 -1次。

2. 游程特性

在序列 a 的一个周期中，由GF( q )中的每个元素构成的长度为 r （1≤ r ≤ n -2）的游程恰好出现( q -1) 2 q n-r -2 次；由GF( q )中每个非零元素构成的长度为 n -1的游程恰好出现 q -2次；长度为 n -1的游程恰好出现 q -1次；GF( q )中的每个元素构成的长度为 n 的游程恰好出现1次。

3. 两值自相关特性

序列 a 的周期自相关函数是二值的，即

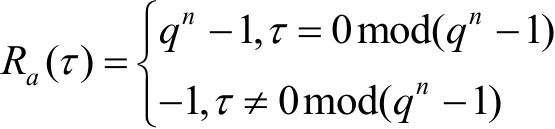
如果序列 a 满足上述3个条件，那么称序列 a 具有理想自相关函数。 OxzO6jf9jbS48bRIMPvn5aWJ7F5IxtawIvknjFGsY5wMwYeCclkuIhnn5wLKugDC