下载掌阅APP，畅读海量书库
立即打开
2.2节主要介绍了几种典型时间离散混沌系统。混沌系统的伪随机性、非周期性、初值敏感性等特征有利于将信号加密或遮掩，因此混沌系统在图像加密、多址通信、跳频通信中具有广阔的应用空间。将时间离散混沌系统应用于数字通信加密或模拟信号加密，有一个关键的问题不能忽视，就是通信双方在公开信道传输时需要考虑的同步问题。在20世纪末，即混沌保密通信研究的起步阶段，相关研究工作主要围绕如何将混沌信号从复杂噪声背景中提取和恢复出来，这些问题的研究成果开辟了混沌同步研究的先河，后续研究主要集中于如何在保证通信效率的同时，提高混沌系统的同步性能，也就是通信的稳健性。近年来，随着混沌保密理论研究的不断深入，经典通信理论的同步方法和手段逐步被引入混沌保密通信领域，这类研究的一个最主要基础就是在混沌动力学基础上的同步理论。
Pecora和Carroll偶然发现的混沌同步开创了混沌同步概念的先河，使混沌同步重构这一困扰学者的难题得以解决。这标志着混沌系统的理论研究有了新的理论支撑，为混沌保密同步的实现提供了理论依据。
混沌同步的本质就是两个不同构型和参数的混沌系统（可以是同一类映射，也可以是不同映射），从不同初始条件出发，使其轨道随着时间的推移逐渐趋向一致并保持同步，并且这种同步结构是稳定的。由于混沌自身的特点，与传统的控制方法相比，其目标并不是抑制混沌，而是将两个混沌系统控制在同一个混沌轨道上。混沌同步的定义有很多，本节重点介绍一种典型的数学描述方法。
定义2.1 混沌同步
假设存在两个混沌映射系统
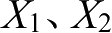，且两个混沌映射系统具备不同的初始状态
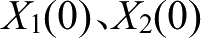，那么只要在
t
时刻满足
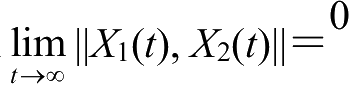，则混沌系统
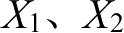满足混沌同步。
双向耦合或在系统的外部信号驱动下，若 t →∞时两个系统的内部状态 x 和 y 趋向一致，则可以称这两个系统发生了完全同步。其同步误差一般定义为
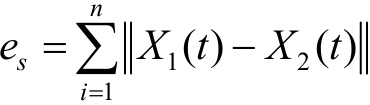
通常仅对分量误差 ẏ = F ( y , s ( t ））的演化进行分析即可。基于定义2.1，衍生出关于混沌同步的4个子定义，即同步包括以下4种类型。
完全精确同步是最早研究的混沌同步状态，它是指两个结构和参数一致的混沌系统在演化过程中，通过驱动耦合或在相同外部信号的扰动下，对于所有时间
t
，满足
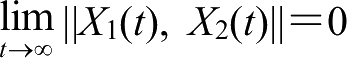。这表示两个混沌映射系统可能精度不高或在时域范围内完全同步。
完全不精确同步是指两个结构和参数不完全一致的混沌映射系统在演化过程中，在通过驱动耦合或在相同外部信号的扰动下，有
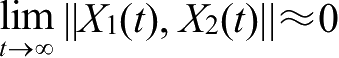。这表示两个混沌映射系统可能精度不高或在时域范围内不完全同步。
至少存在一个状态值
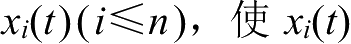对于同步误差
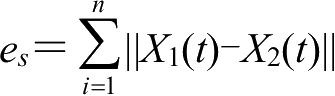满足：存在
n
≥
t
≥0，使
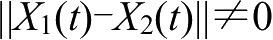，也就是在所有状态之中，总有满足使两个映射系统耦合达到同步的状态。
在研究混沌映射系统时，由于两个混沌系统之间的维度不同，不可能实现传统意义上的完全同步或广义同步。相同步与传统通信中的相位同步概念相同。混沌的相空间特性是其特有的性质之一，而相空间同步对于保密通信系统来说是具有非常重要意义的，特别是研究参数未知或状态未知的混沌映射系统，利用相空间同步方法可以有效预测和跟踪混沌信号。
近年来，混沌理论研究逐步深入，混沌同步控制的方法包括：驱动-响应同步、主动-被动同步和微扰反馈同步等。对于微扰反馈同步，可以用自动控制法、Lyapunov直接法、反向单步设计法和变结构控制法来确定控制扰动量。
驱动-响应同步（PC同步）是Pecora和Carroll提出的经典混沌同步控制方法，这一技术被成功应用于混沌掩盖通信。该方法的特点是两个混沌映射系统是耦合的，系统之间存在驱动和响应关系，这种驱动和响应关系也是该方法实现同步的主要手段。
PC同步的必要条件为响应系统的最大条件Lyapunov指数为负。条件Lyapunov指数是PC模型中提出的配套概念，所谓条件是指Lyapunov指数与控制信号有关，这里是指响应系统的Lyapunov指数是以驱动变量为前提条件的。
设存在某个 n 维混沌动力学系统，记为 Ḋ = f ( D )，将该系统分解为两个混沌子系统，记为
式中， D ={ d 1 , d 2 , …, d n }， V ={ v 1 , v 2 , …, v m }， W ={ w 1 , w 2 , …, w m }。式（2.21）和式（2.22）被称为驱动系统，现在复制一个响应系统，即
Ẇ = h ( V, W ) （2.23）
式中， V 为驱动变量，由驱动系统产生，用来驱动响应系统。而同步的Lyapunov指数的稳定判据是，当响应系统式（2.21）和式（2.22）的所有条件Lyapunov指数都为负时，才能达到驱动和响应系统的同步，即
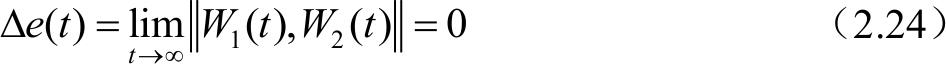
PC同步作为典型的非线性动力学系统的同步控制方法，由于其物理特性，某些混沌系统无法分解为两个子系统，这时PC同步将无法实现，可见PC同步也有其适用范围。
1995年，L. M. Pecora等人提出了具有普适效果的主从分解模型（Active- Passive Decomposition），也称主动-被动分解模型。
假设存在自治动力学系统：
可被改写为非自治动力学系统形式：
式中， s ( t )为驱动信号，其中两个系统的误差动力方程为
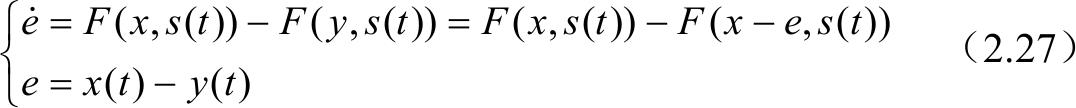
若在 e =0处有一个稳定点，则式（2.27）中两个系统存在同步流形 x ( t )- y ( t )。
通常， s ( t )与系统的状态 x 和信号 i ( t )均存在关系，即
s ( t )= h ( x , i ( t ））或 S = h ( x , i ( t ), s ) （2.28）
变量反馈模型（Variable Feedback Control）本质上沿用经典反馈控制理论，即应用混沌控制中的变量对原混沌系统提供反馈。这里的反馈有连续和离散之分，也有文献称其为连续反馈，与同脉冲反馈控制相区别，其基本思想如式（2.29）和式（2.30）所示。响应驱动系统方程较驱动系统增加了一个反馈器，根据Lyapunov稳定性原理，可设计保证同步实现的反馈项，即
ẋ = f ( x ) （2.29）
ẏ = f ( y )+ C ( x, y ) （2.30）
式中， C ( x , y )为适当的反馈控制函数，可以是线性函数，也可以是非线性函数。
如何设计出优良的反馈控制函数是同步控制的关键，混沌同步与混沌控制在稳定性问题上的一致性，使许多控制领域中的技术都可以用于设计反馈控制函数。其主要控制方式包括滑模控制方法、基于状态观测器的控制方法等。由于反馈控制函数的设计方法种类众多，微扰反馈同步模型已成为最简单有效并被广泛采用的一种同步模型。
此外，还可以考虑将多种同步控制方式进行分段组合实现控制，选择其中容易实现的合适形式。由于这种同步方法可以在复制系统上重现原始系统所有状态变量的演化，因而可以使同步化在混沌通信中的应用更为方便。除上述3种典型的同步方法外，近年来，新的控制理论逐步被引入混沌控制领域，如自适应同步方法、神经网络同步方法等。随着控制理论研究的不断深入，新的同步控制技术一定会越来越多。混沌同步之所以成为研究热点，其根本原因在于“要通信，先同步”是实现混沌保密通信的关键。今后混沌控制技术发展仍是研究热点，特别是与混沌通信紧密联系在一起的控制技术。