下载掌阅APP，畅读海量书库
立即打开
混沌来自系统的非线性性质，但是非线性只是产生混沌的必要条件而非充分条件。如何判断给定的系统是不是存在混沌运动，以及如何用数学语言描述混沌运动，并对其进行刻画，是一项具有创造性的工作。目前，国内外学者大都采用公式推导和数值实验来判断一个系统是否存在混沌运动，然后通过物理实验，如构建混沌电路等仿真手段，加以验证。
描述混沌状态的物理量有Lyapunov指数（Lyapunov Exponent，LE）、Kolmogorov熵、功率谱和Poincare映射等。其中，Lyapunov指数、Kolmogorov熵和分形维是定量化描述指标，具有独特的优点；此外，Lyapunov指数是研究混沌控制、反控制和混沌同步的一个重要特征量，也是混沌控制、反控制和同步的重要物理机制所在，所以研究Lyapunov指数计算方法具有重要意义。
Lyapunov指数是一种定量描述动力系统轨道局部稳定性的方法 [95] ，设相空间中一点 x (0)有半径为 ε (0)的邻域，该邻域随着动力系统的演化向相空间各方向延伸，形成一个超椭球，超椭球在各方向上的轴长为 ε i ( t )，则轨道 x ( t )在 i 个方向上的Lyapunov指数定义为
轨道在各方向上的Lyapunov指数共同组成Lyapunov指数谱，其中最大的Lyapunov指数对系统性质起决定性作用，因此被称为该系统的Lyapunov指数。Lyapunov指数刻画了在局部范围内轨道间的分离程度，若Lyapunov指数为正，则表示相邻轨道发散，说明系统具有混沌特性；若Lyapunov指数为负，则表示系统处于稳定状态，收敛于不动点或出现周期解；若Lyapunov指数为零，则分支点对应稳定轨道的边缘，系统处于临界状态。总之，Lyapunov指数的正、零和负分别表示系统是混沌的、临界的和稳定的状态。
对于高于一维的系统，存在Lyapunov指数的集合，称之为Lyapunov指数谱。Lyapunov指数谱中的每个Lyapunov指数都刻画了系统运行轨迹在某一特定方向的收敛或发散特性。例如，三维相空间的所有奇异吸引子都具有同样类型的Lyapunov指数谱（+, 0, -），其中，正Lyapunov指数表示奇异吸引子内部的混沌，零Lyapunov指数表示沿着轨道低于指数速度的运动，而负Lyapunov指数表明相空间包含一个奇异吸引子。在实际应用中，研究最大Lyapunov指数 λ max 具有重要意义，其定义式为
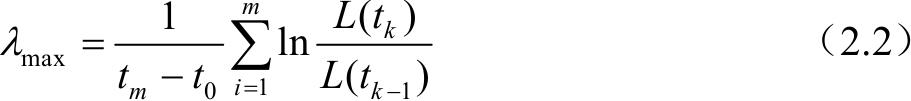
式中， L ( t k )为 t 时刻最邻近两点间的距离； m 为迭代总步数。 λ max 不仅是区别奇异吸引子的指标，而且是混沌系统对初始确定性放大率的定量描述。
混沌轨道的局部不稳定性使其相邻轨道间以指数速率分离，因此在初始测量中无法区分两条轨道，随着时间的推移或迭代步骤的增加，轨道间出现了指数分离的情况，使得再次测量时这两条轨道无法区分。所以不可能通过一次测量来获得关于混沌系统以后的全部变化趋势和信息，即混沌的运动是长期不可预测的，必须通过不断更新测量结果来获得混沌系统产生的信息。为了衡量混沌运动产生信息流的能力，我们引入Kolmogorov熵（K熵）的概念。
设以一定的精度对混沌轨道进行测量，相空间在该精度下被划分为不同的区间，记为{ s i }，我们以相同的时间间隔对轨道进行测量，可以得到符号序列 S m ( x 0 )= s i 1 , s i 2 ,…, s im ，则该符号序列的熵定义为
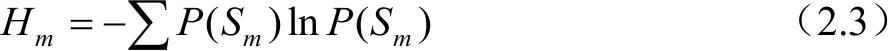
K熵就是熵 H m 随时间增长的速率，设时间间隔为Δ t ，所选择的测量方法为 β ，则该速率可定义为
K熵的取值可以判断系统运动的无规则程度，对于规则运动的确定性系统，其K熵为0；对于随机运动系统，其K熵趋近于无穷大；而对于混沌系统，由于新的测量始终会带来新的信息，所以其K熵大于0。K熵是否大于0，是判断动力系统是否处于混沌运动的有力依据。
谱分析是研究振动和混沌的重要手段。根据Fourier分析，任何周期为 t 的周期运动 x ( t )都可以展成Fourier级数，其系数与相应的频率关系为离散的分离谱，而非周期运动的频率是连续谱。对于随机信号的样本函数， x ( t )的功率谱密度函数定义为
式（2.5）中， R x ( τ ）为 x ( τ ）的自相关函数，即
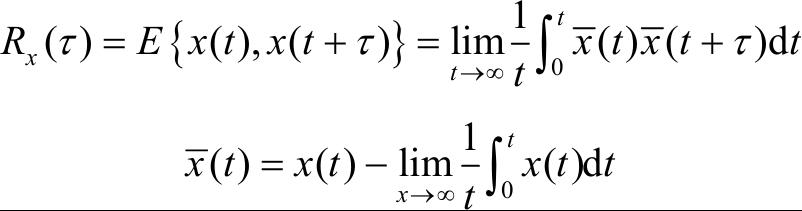
式中， τ 为采样间隔。
对于周期运动，功率谱只在基频及其倍频处出现尖峰。准周期对应的功率谱在几个不可约的基频及由它们叠加的频率处出现尖峰。混沌运动的功率谱为连续谱，即出现噪声背景和宽峰。由于 S x ( w )与 R x ( τ ）互为Fourier正、反变换，它表示序列相关程度。因此，在规则运动的情况下，表示运动的函数产生的序列自相关函数 R x ( τ ）具有常数数值和周期振荡；在混沌运动情况下， R x ( τ ）将按指数迅速衰减到零。
分形维反映了混沌系统在相空间上的几何分布，具有分形结构的奇异吸引子有非整数的分形维数，代表了其在相空间上几何分布的奇异性。
Hausdorff维可以用来描述空间、集合和奇异吸引子的几何性质。 n 维空间中的子集的Hausdorff维数定义为
式中， N ( a )为覆盖集合 S 所需边长为 a 的 n 维超立方体的最小数目。在实际应用中，计算Hausdorff维是基本不可能实现的，因而其主要作用是从理论上了解混沌系统分形的几何性质。
盒子维是应用最广泛的维数之一，因为这种维数的数值计算方法及其经验估计相对容易。设 S 是 n 维空间中的任意非空有界子集，对于每个 r →0， N ( S , r )表示用来覆盖 S 的半径为 r 的最小闭球数，若
存在，则 S -盒子的维数为
盒子维数有许多等价定义，主要区别在于盒子的选取，式（2.8）中选择的盒子为闭球，根据实际情况还可以选择线段、正方体或立方体。盒子维数特别适合科学计算，用数值计算的方法求出Logistic映射 x n +1 =3.57 x n (1- x n )奇异吸引子的盒子维数约为0.75（选择 r =3×10 -6 ）。
从几何直观角度考虑，具有正Lyapunov指数和负Lyapunov指数的方向都对扩张成奇异吸引子起作用，而负Lyapunov指数对应收缩方向，在抵消膨胀方向的作用后，提供奇异吸引子维数的非整数部分。因此，我们将负Lyapunov指数从最大的
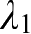开始，把后续的Lyapunov指数逐个相加。若加到
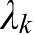时，
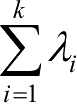为正数，而加到下一个
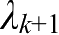后，
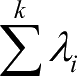为负数，则可用线性插值来确定维数的非整数部分。奇异吸引子的Lyapunov指数定义为
式中，
k
为使
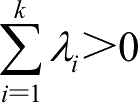成立的最大整数。
Lyapunov指数对描述奇异吸引子非常有用，对 n 维空间来说有以下结论。
（1）定常吸引子： λ 1 <0, λ 2 <0, …, λ n <0，此时Lyapunov维数为0，对应平衡点（不动点）。
（2）周期吸引子： λ 1 =0, λ 2 <0, …, λ k <0, …, λ n <0，此时Lyapunov维数为1，对应平衡点（周期点）。
（3）准周期吸引子： λ 1 =0, λ 2 =0, …, λ k =0, …, λ k +1 <0, …, λ n <0，此时Lyapunov维数为0，对应平衡点（准周期吸引子）。
（4）混沌吸引子：有0< k < n ，并且 S k <- λ k +1 =| λ k +1 |，此时Lyapunov维数总是分数（ k < d L < k +1）。
混沌信号并非随机却貌似随机，具有非周期性、连续宽带频谱、类噪声的特性，具有异常复杂的运动轨迹和不可预测性，使它具有天然的隐蔽性，适合作为保密通信的载体。一般而言，混沌保密通信会在发送端把信息表示成具有混沌特性的波形或者码流；会在接收端从接收到的信号中恢复出正确信息。在公共信道中，混沌信号是信息的载体，在多数情况下，这个信号又作为同步发送端和接收端混沌系统的信号。另外，混沌系统本身是具有确定性的，完全由非线性系统的方程、参数和初始条件决定，从而易于产生和复制出数量众多、非相关、类随机而又确定的混沌序列。混沌信号的隐蔽性、不可预测性、高度复杂性和易于实现的特点使它特别适用于保密通信。混沌保密通信要求发送端和接收端的混沌系统同步，这样混沌同步就成了混沌保密通信的关键问题和重要的理论基础。