




统计学这门学科通常比较枯燥、一成不变或者专业性很强,但现代社会的方方面面几乎都与之相关。它可以告诉我们一种新研发的药品对治疗癌症是否有效;还能帮助农产品检验人员判断我们的食品是否安全;它还可以指导和解释民意调查;在商业上,我们运用统计方法进行市场调查和广告推广;在体育领域,统计学经常作为运动员和团队排名的方法。实际上,你会发现在某些重要领域几乎任何话题都与统计学有关。
本书最基本的目标是帮助读者学习一些统计方法背后的核心思想。值得称道的是,即使本书包含很少的统计理论,书中大量的案例也能帮助你理解在新闻、课堂、工作地点,或者在日常生活中所遇到的统计问题。
在统计信息中,虽然有时候把单词data看作information的同义词,但实际上它是复数。在只有一则信息的时候叫作datum,当有两则或两则以上信息时才称作data。
我们从统计自身的定义开始学习。统计这个单词在英语中用作单数和用作复数时,意思是不一样的。当被看作单数时,统计是帮助我们理解如何去收集、整理和分析一些话题中的数据或其他信息的科学方法,在这里把数和其他信息作为参考数据。当被看作复数时,统计是描述某些事物属性的实际数据。例如,你的班里有30个学生,他们的年龄是17~64岁。在这里,“30个学生”“17岁”和“64岁”,从不同角度来说都是描述你所在班级某些属性的统计数字。
统计的两个定义
·统计是对某一现象有关数据的搜集、整理和分析。
·统计是描述、总结某种现象的数据或其他信息。
根据新闻报道,1.113亿美国人看到纽约巨人队取得了超级碗橄榄球比赛的冠军,这就解释了,为什么一条30秒的商业广告的价格为300多万美元。那么是谁统计了这几亿人的数据?
统计学起源于一些国家事务,如人口普查数据和税金数据的采集。这就是为什么统计(statistics)这个词的词根是国家(state)。
答案是没有人统计这些数据。1.113亿美国人观看超级碗橄榄球比赛的这个数据来自于一家名为尼尔森媒介研究(Nielsen Media Research)的调查公司的统计研究结果。这家公司仅仅通过监控5000个住户的收视习惯,就编制出了著名的尼尔森收视率。
如果你是统计学的初学者,那么会认为尼尔森所得的结论更像是一个延伸。只研究几千个数据怎么能得出关于上亿人的结论?然而,统计科学表示,只要统计研究设计精准,这个结论就相当准确。下面我们以超级碗的尼尔森收视率为例,研究一些关键问题来论证通常情况下的统计研究如何进行。
尼尔森的研究目标是确定美国观看超级碗橄榄球比赛的总人数。用统计学的专用术语表示,尼尔森所研究的所有美国人是一个总体;尼尔森所希望确定的数据,即观看超级碗橄榄球比赛的总人数,是这个总体的一个主要特征,在统计学中,这个总体特征被称为总体参数。
我们通常认为总体表示一群人,其实它可以是任意一个群体——人、动物或者事物。例如,在一个有关汽车安全的研究中,总体可以是在路上行驶的所有车辆。同样,总体参数这个术语,可以解释为总体的任何一个特性。在上例中,总体参数可以是某一时间段内所有行驶车辆的数量、行驶车辆的事故率或者行驶车辆的载重范围等。
总体 :在统计研究中,总体是所研究的人或事物的完整集合。
总体参数 :总体中对某变量的概括性描述。
例1 总体和总体参数
根据下列情况,描述研究的总体,并确定感兴趣的总体参数。
a.你在农夫保险公司工作,公司要求你确定在没有侧面撞击安全气囊的车祸事故中,对受害者赔付的平均金额。
b.你被麦当劳录用,确定每周用于炸薯条的土豆用量。
c.你是美国基因泰克公司下属的一个商业记者,正在调查一个新的治疗办法对儿童白血病是否有成效。
答案 a.总体包括所有的没有侧面撞击安全气囊的车祸事故中已经拿到保障金的受害者。相关的总体参数是对受害者赔付的平均金额(在之后的章节中,“average”将会被一个更准确的术语“mean”代替)。
b.总体包括每周运输过来的用于炸薯条的土豆重量。相关的总体参数是土豆的平均重量,以及其重量的差异(例如,大多数每周用量是接近还是远高于平均值)。
c.总体包含所有患白血病的儿童。其中重要的总体参数是没有用新治疗办法就痊愈的儿童百分比以及使用新治疗办法后痊愈的儿童百分比。
如果尼尔森的研究是无所不能的,它就能通过调查每个美国人来确定观看超级碗橄榄球比赛的人数。但现实中没有人能做到这样的全面调查,所以他们尝试研究相关的小集体来估计观看比赛的人数。尼尔森尝试通过监控美国人的一个较小样本群体,来研究所有观看比赛的美国人这个总体。尼尔森在大约5000个家庭中安放了记录装置,所以这些家庭的人们就成为尼尔森所研究的美国人样本。
亚瑟·C.尼尔森(Arthur C.Nielsen)在1923年建立公司并发明市场调查。1942年,他推出了尼尔森广播指数为广播节目定级,并在20世纪60年代把该方法扩展到电视节目领域。该公司现在也监测其他媒介(互联网、智能手机等),并不断地改变方法来适应新的媒介技术。
尼尔森从5000个家庭中收集的个体测量值组成了原始数据。它收集了很多原始数据,比如每个家庭在什么时候收看电视,收看多久,播放什么节目,谁在看等。尼尔森把这些原始数据组合成一系列描述某个样本特征的数据,比如样本中观看个别节目的观众百分比或者样本中观看超级碗橄榄球比赛的总人数。这些数据被称作样本统计量。
样本 是总体的一个子集,它的数据是进行实际测量而获得的。
原始数据 是对样本进行实际测量或观测所收集的数据。
样本统计量 是描述从原始数据中筛选总结的样本特征的数据。
美国劳工部定义,一些没有工作的人并不是失业。例如,家庭主妇或者家庭主夫都不计入失业人群,除非他们在很积极地尝试寻找工作。那些试图寻找工作最后却因挫折而放弃了的人也不算在失业人群中。
例2 失业调查
美国劳工部把城市劳动力定义为那些已就业或正在积极寻找就业机会的人。每个月,劳工部会报告失业率,其是指在全部城市劳动力中积极寻找工作的人的比率。为确定失业率,劳工部调查了60000个家庭,在失业率报告中,对以下术语进行描述:
a.总体 b.样本 c.原始数据 d.样本统计量 e.总体参数
答案 a.总体是美国劳工部想要研究的构成城市劳动力的群体。
b.样本是指60000个家庭调查中的所有人。
c.原始数据是指调查中收集到的所有信息。
d.样本统计量是对样本中原始数据的总结。在本例中,相关样本统计量是指积极寻找工作的人所占的百分比(劳工部同样也计算其他样本统计量,如青年、男性、女性和退伍军人的失业率)。
e.总体参数是指与样本统计量对应的总体特征。在本例中,相关总体参数是实际失业率。需要注意的是,劳工部并没有实际测算总体参数,只是从样本中收集数据来估计总体参数。
假设尼尔森调查发现5000个家庭的样本中,有31%的人观看超级碗橄榄球比赛。“31%”是样本统计量,它是对样本的描述。但尼尔森真正想了解的是相应的总体参数,是观看超级碗比赛的人占所有美国人的百分比。
尼尔森的调查者没有办法准确了解总体参数的数值,因为他们只研究了一个样本。然而,他们希望所做的工作可以保证样本统计量是总体参数很好的估计值。换句话说,他们希望得出结论,因为样本中31%的人观看超级碗,所以总体中也会有近31%的人观看。统计学的一个主要目标就是帮助调查者评估这类推论的有效性。
思考时刻
假设尼尔森的结论是30%的美国人观看超级碗橄榄球比赛。这表示有多少人观看比赛?(美国的总人口接近3.1亿。)
统计科学提供了一种方法,使得调查者能够确定样本统计量可以很好地估计总体参数。例如,调查或投票结果经常涉及误差幅度的概念。通过加减误差幅度,可以得到样本统计量的区间(即置信区间),它很可能包含总体参数。在大多数情况下,误差幅度被定义为该范围包含总体参数的置信度为95%。我们将在第八章讨论有关“可能”和“95%置信度”的精确定义。《纽约时报》( The New York Times )上有一个十分有用的解释(如图1-1所示)。在尼尔森案例中,误差幅度是1%。因此,如果样本中31%的人观看超级碗橄榄球比赛,那么总体中有30%~32%的人观看超级碗比赛的这个结论有95%的置信度。

图1-1 民意调查中的误差幅度
统计学最重要的一个标志性发现是,可以从非常小的样本中得到有意义的结果。然而,样本容量越大越好(当可行的时候),因为通常情况下,样本容量越大,误差幅度就越小。例如,在一个设计良好的投票选举中,在95%的置信区间内,当样本容量为400时,误差幅度通常为5%;当样本容量为1000时,误差幅度下降到3%;而当样本容量为10000时,误差幅度为1%(参考第八章,了解怎样计算误差幅度)。
统计研究中的 误差幅度 描述了一个很可能包含总体参数的值域或 置信区间 。置信区间可以通过样本统计量加减误差幅度获得。也就是说,很可能包含总体参数的值的范围是:从(样本统计量–误差幅度)到(样本统计量+误差幅度)。
误差幅度通常给定95%的置信区间,这意味着在研究中有95%的样本会得出此区间将包含实际的总体参数(5%的样本不会)。
例3 政治性丑闻
皮尤人口和压力研究中心共计采访了1002个美国成年人,调查政治性丑闻在最近的官方选举中有所增加的原因。57%的被采访者声称,其增加的原因是丑闻都暴露在媒体更强有力的监督下,而19%的人则认为增加的原因是道德水准的下降。投票的误差幅度为3%。请描述这次调查的总体和样本,并对57%的样本统计量作解释。我们如何推断出总体的百分比?即总体人群中“相信政治性丑闻的增加是由于媒体愈加强有力的曝光性”这部分人群的百分比。
答案 总体是所有成年的美国人,样本是1002个被采访的美国成年人。样本统计量的57%是样本中实际回答“政治性丑闻的增加是由于媒体愈加强有力的曝光性”的百分比。根据57%的样本统计量和3%的误差幅度,可以确定取值范围:从57%–3%=54%到57%+3%=60%。这个范围很可能包含总体参数(95%的置信区间)。
思考时刻
例3所描述的调查中,被采访者只在两个可能的答案——媒体高曝光率和日益下降的道德准则——中做选择。如果被采访者可以自己给出答案,你认为结果会改变吗?请解释。
统计学家通常把这个学科分为两个主要的分支:描述统计,即通过图表和样本统计量对原始数据进行处理;推断统计,即利用样本数据来推断总体特征。本书中,第二至第五章介绍描述统计,第六至第十章介绍推断统计。
尼尔森媒体调查的步骤也可以应用于其他统计研究中。图1-2和下面的框图总结了统计研究的基本步骤。注意这些步骤有些理想化,实际上每个研究的情况都不太相同。而且,这些基本步骤中隐藏的细节问题十分重要。例如,在步骤2中,一个选择不当的样本可能使整个研究毫无意义。从小样本中得出有关总体的结论需要格外谨慎。
统计研究的基本步骤
步骤1:明确表述研究的目标。确定想研究的群体以及想了解的内容。
步骤2:从总体中选择有代表性的样本。
步骤3:从样本中收集原始数据,通过计算感兴趣的样本统计量来总结数据。
步骤4:使用样本统计量对总体进行推断。
步骤5:得出结论,确定是否达到目标。
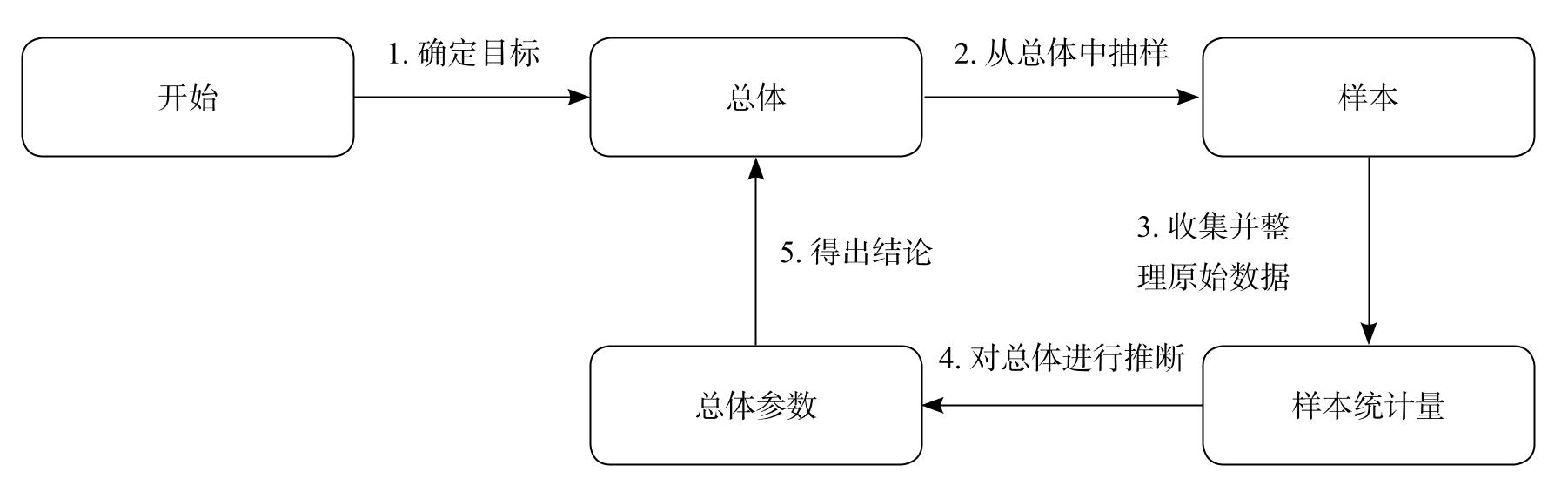
图1-2 统计研究的基本步骤
例4 确定步骤
确定例3中调查者进行统计研究的五个步骤。
答案 a.调查者以“美国人如何看待最近政治性丑闻增加的原因”为目标,以所有美国成年人为总体,谨慎地将儿童排除在外。
b.选择1002个美国成年人作为样本。虽然并未说明样本是如何选取的,但我们可以假设这1002个美国成年人包含总体美国人的所有类型。
c.调查者通过投票收集原始数据。所有的原始数据都是独立的回答。通过计算样本统计量总结归纳数据,如每个问题中回答是或否的人数所占的百分比。
d.调查者可以通过统计技术推断总体特征。在本例中,包含推断相关总体参数、计算误差幅度。
e.调查者通过计算确保正确研究和解释估计的总体参数,得出有关全体美国人对近期丑闻态度的结论。
到目前为止,我们讨论的大多数案例涵盖了调查和投票,而统计学所包含的内容不仅仅是这些,比如用实验检验新药品的治疗效果,分析全球变暖的危害,或者评估大学教育的价值。实际上,统计学的主要目标是帮助我们在面对很多可能的选择时做出恰当的决策。
统计学的目的
统计学有很多用处,而它最重要的目的是帮助我们在面对不确定的问题时做出决策。
我们讨论的大多数案例都基于以上目的,但偶尔也会讨论一些看似比较抽象的理论。如果记住了所有统计的目的,你最终会通过这些理论了解我们的世界。以下案例将会带给你一些启示,它包括在20世纪公共卫生方面取得巨大成就的一些重要理论。
在研发了索尔克疫苗后,小儿麻痹症在美国迅速减少,但在一些不发达国家这种病还是很常见。1998年,全球开始大力支持为儿童注射索尔克疫苗。尽管现在还没有达到完全根除这个疾病的目标,但对小儿麻痹症的抑制已经非常成功了。
工作的最大报酬,乃是获得可以做得更多的机会。
——乔纳斯·索尔克
案例研究 索尔克脊髓灰质炎疫苗
在20世纪四五十年代,如果你是一位家长,你最害怕的就是小儿麻痹这种疾病。在这个小儿麻痹症肆虐的时期,每年都会有数以千计的儿童因为这个病而瘫痪。1954年,乔纳斯·索尔克(Jonas Salk,1914—1995年)医生对新研制出的疫苗进行有效性实验。实验的样本为从美国所有儿童中选出的40万名儿童,其中的一半儿童注射了索尔克疫苗,而另一半只注射了生理盐水(生理盐水是安慰剂,见1.3节)。在注射索尔克疫苗的儿童中,只有33人患了小儿麻痹症。而未注射疫苗的儿童中,有115人患上了小儿麻痹症。通过统计分析,调查者认为疫苗对抑制小儿麻痹症有效。因此他们决定大力支持并改进索尔克疫苗,并为所有儿童注射。感谢索尔克疫苗,让恐怖的小儿麻痹症成为过去的一个回忆。