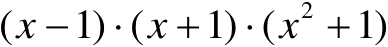(1)代数的基本含义是用字母来代表数、代表式。
(2)代数式:用基本的运算符号(加、减、乘、除、乘方、开方)把数或表示数的字母连接而成的式子,称为代数式。实数的运算规律也适用于代数式。单独的一个数或字母也是代数式。
(3)代数式的值:能用具体的数值代替代数式中的字母,按照代数式指明的计算,计算出的结果称为代数式的值。
(1)列代数式:把简单的与数量有关的词语用代数式表示出来,称为列代数式。
(2)公式:用等号连接起来的两个代数式,实际意义是表示物理量之间关系或数学运算关系的式子。
(1)代数式分类如下:
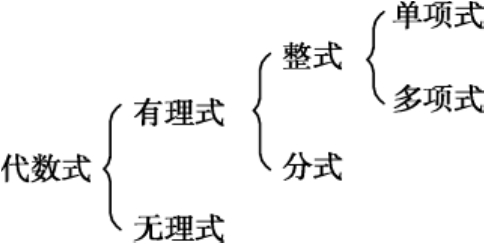
(2)单项式和多项式统称整式。
(3)分式:如果 A 、 B 为整式, B 中含有字母,式子 A / B 称为分式。
【例3】 说出下列代数式的意义。
(1)
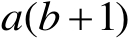 (2)
(2)
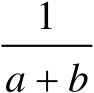
解: (1) a 乘以 b 与1的和的积。
(2) a 与 b 之和的倒数。
【例4】
当
a
=0,
a
=
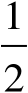 ,
a
=0.6时,求代数式
,
a
=0.6时,求代数式
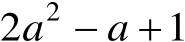 的值。
的值。
解: (1) a =0时,有
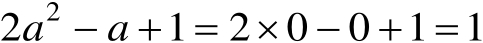
(2)
a
=
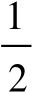 时,有
时,有
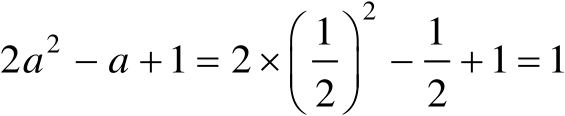
(3) a =0.6 时,有
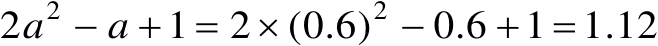
1.判断下列各式哪些是代数式,哪些不是代数式。
(1)
x
+
y
(2)3(
a
+
b
) (3)
S
=
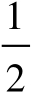 ab
ab
(4)5+3+2 (5)0 (6) a + b = x + y
2.求代数式
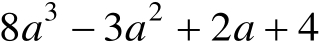 的值。
的值。
(1)
a
=0 (2)
a
=
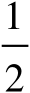 (3)
a
=-1
(3)
a
=-1
3.用代数式表示:
(1)比 x 大5的数与比 y 少8的数的和。
(2)两个数 a 、 b 的平方和与这两个数积的差的倒数。
(3)每件上衣售价 a 元,降价10%后的售价。
4.一个长方形纸箱,它的长是 a ,宽是 b ,高也是 b ,试写出这个纸箱的体积公式。
(1)单项式:不含加法或减法运算,都是数字与字母的积,这样的整式称为单项式。
(2)单项式系数:单项式中的数字因数(包括前面的符号)。
(3)单项式次数:单项式中所有字母的指数的和。
【例5】 指出下列各单项式的系数和次数。
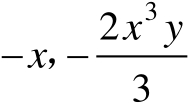
解: (1) - x ,系数为-1,次数为1。
(2)-
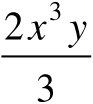 ,系数为-
,系数为-
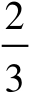 ,次数为4。
,次数为4。
(1)多项式:多个单项式的代数和。
(2)多项式的项:多项式中每一个单项式称为多项式的一项,有几个单项式称为几项式。多项式中不含有字母的项称为常数项。
(3)多项式的次:多项式中,次数最高的单项式的次数是多项式的次。
(4)多项式排列:
①降幂排列,即把一个多项式按其中某一个字母的指数由高到低的顺序排列。
②升幂排列,即把一个多项式按其中某一个字母的指数由低到高的顺序排列。
【例6】
指出多项式
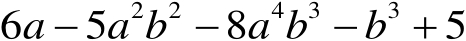 是几次几项式,其常数项是多少?并按字母
a
降幂顺序重新排列。
是几次几项式,其常数项是多少?并按字母
a
降幂顺序重新排列。
解: 多项式为七次五项式,常数项为5。
降幂排列为
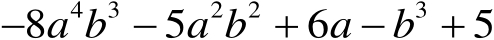
(1)同类项:多项式中所含字母相同且相同字母的指数分布对应相等的项。
(2)合并同类项:多项式中,凡同类项均可进行合并,合并的法则是系数与系数相加作为新的系数,字母和字母的指数不变。
(3)去括号和添括号:括号前面去掉(或添上)“+”号,括号内各项符号不变;括号前面去掉(或添上)“-”号,括号内各项都变号(正变负,负变正)。
【例7】 判断下列两个单项式是不是同类项。
(1)
 (2)
mn
和-4
nm
(2)
mn
和-4
nm
(3)
 (4)8与8
b
(4)8与8
b
解:
(1)
 不是同类项。
不是同类项。
(2) mn 和-4 nm 是同类项。
(3)
 不是同类项。
不是同类项。
(4)8和8 b 不是同类项。
【例8】 合并同类项:
(1)
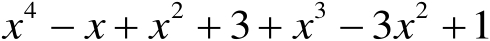
(2)
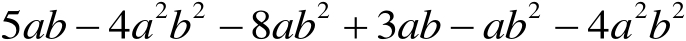
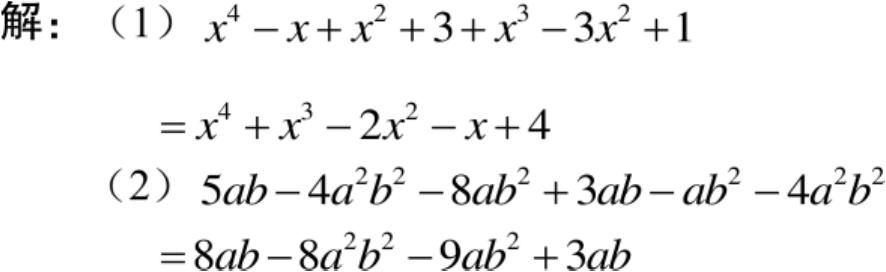
【例9】 对多项式4 a –(3 a -5 b -7 c) +3(-2 c +5 b )去括号。
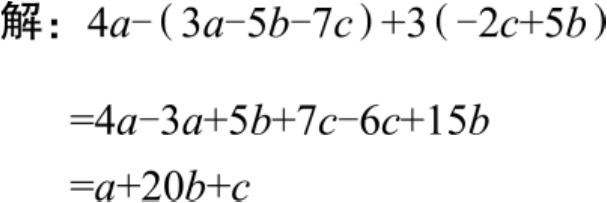
(1)整式的加减运算实际上就是合并同类项。
(2)运算的步骤是先去括号,再合并同类项。整式的加减结果仍为整式。
【例10】 计算:
(1)
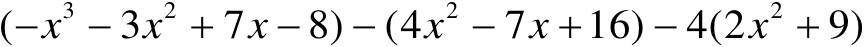
(2)
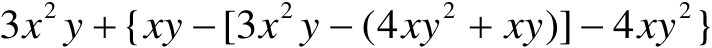
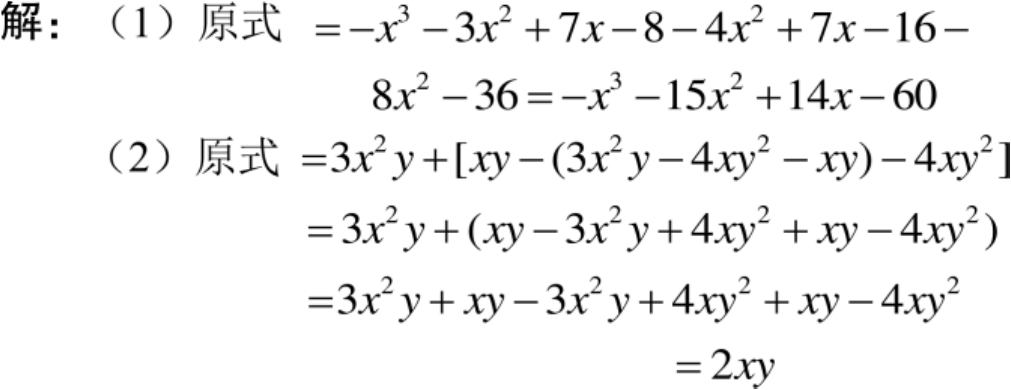
(1)
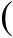 3
a
+5
b
3
a
+5
b
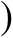 -
-
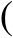 5
a
-7
b
5
a
-7
b
 -
-
 2
a
-4
b
2
a
-4
b
(2)
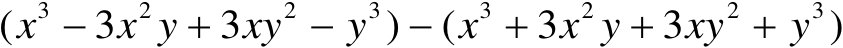
(1)
A
=
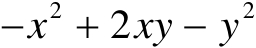 ,
B=
,
B=
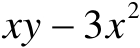 ,
C=
,
C=
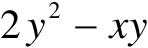 ,求
A
-2
B
+3
C
。
,求
A
-2
B
+3
C
。
(2)5
a
+
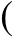 -2
a
-2
a
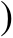 -[3×
-[3×
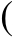 a
-1
a
-1
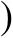 -4
-4
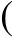 2
a
+1
2
a
+1
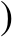 ],求
a
=-1的值。
],求
a
=-1的值。
a m a n = a m + n
a m ÷ a n = a m - n
( a m ) n = a mn
( ab ) n = a n b n
(1)积的系数为各个因式系数的积。
(2)相同字母相乘,按同底数幂的运算法则进行合并。
(3)保留仅在一个单项式中出现的因式。
(1)法则:单项式与多项式相乘,就是用单项式去乘多项式的每一项,变成单项式的乘法。
(2)对乘积进行合并同类项整理。
(1)法则:用一个多项式的每一项乘以另一个多项式的每一项,再把所得的积相加。
(2)对乘积进行合并同类项整理。
( a + b )( a - b )= a 2 - b 2
( a + b ) 2 = a 2 +2 ab + b 2
( a - b ) 2 = a 2 -2 ab + b 2
( a + b )( a 2 - ab + b 2 )= a 3 + b 3
( a - b )( a 2 + ab + b 2 )= a 3 - b 3
( a + b ) 3 = a 3 +3 a 2 b +3 ab 2 + b 3
( a - b ) 3 = a 2 -3 a 2 b +3 ab 2 - b 3
【例11】 化简:
(1)
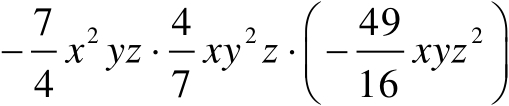
(2)
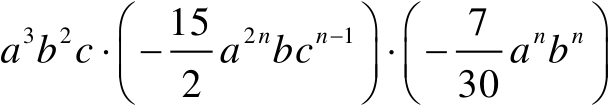
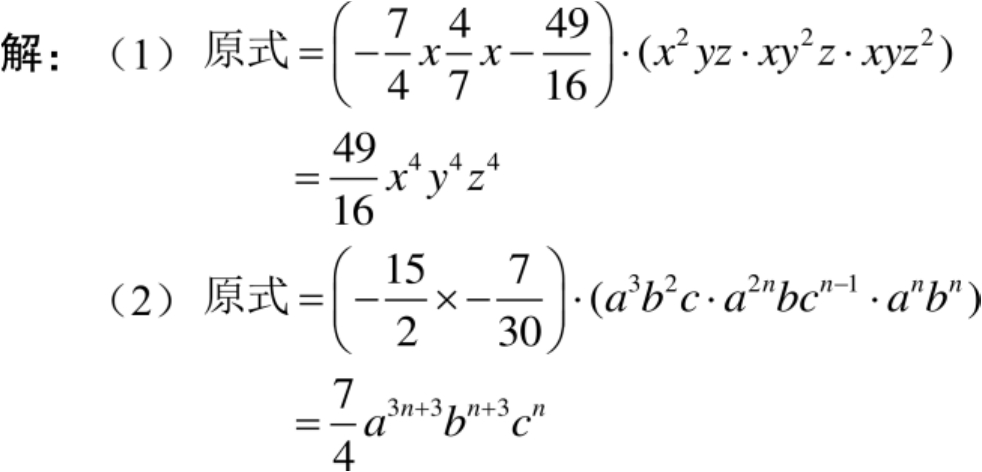
【例12】 化简:
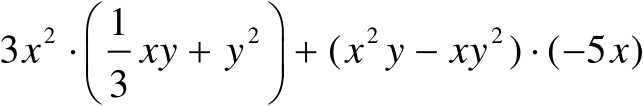
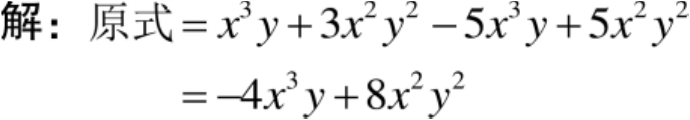
【例13】
化简:
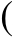 2
a
+3
2
a
+3
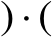 2
a
-5
2
a
-5
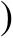 。
。
解:
原式
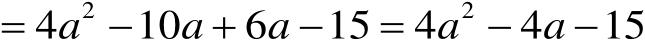
(1)
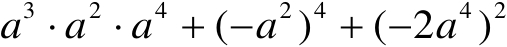
(2)
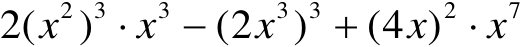
(1)
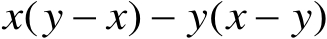
(2)
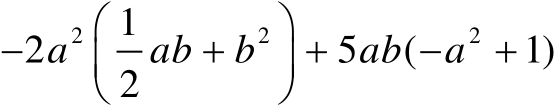
(3)
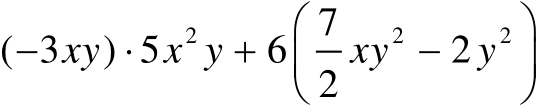
(1)
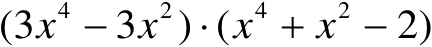
(2)