





一阶电路仅由储能元件的初始状态引起的响应称为零输入响应,即没有外界输入;仅由独立电源引起的响应称为零状态响应,即储能元件没有初始储能。
对于一个动态电路,仅由储能元件的初始状态引起的响应称为零输入响应(Zero-Input Response),此时 u C (0 + )≠0或 i L (0 + )≠0,即一阶电路的输入为零。
1.RC电路的零输入响应
如图2.4.1(a)所示电路,在 t <0时开关S在1端,电压源 U 0 通过电阻 R 1 对电容充电,充电完成时电容电压初始值为 U 0 ,此时电路处于稳定状态;在 t =0时发生换路,开关S迅速由1端转换到2端,如图5.4.1(b)所示。电容脱离电压源而与电阻 R 连接,此时无信号源作用,称为零输入响应,电容通过电阻放电,电容中的电场能通过电阻转化成热能而不断损耗,而电容的电压变为0。注意RC电路的零输入响应,电容的状态是由电压源 U 0 决定的,而不是由 U S 提供的。
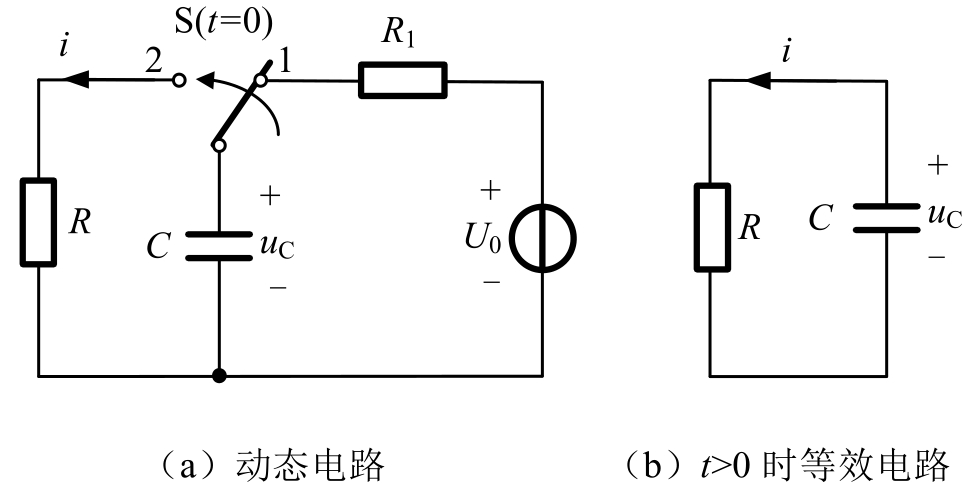
图2.4.1 RC电路的零输入响应
根据三要素式(2.3.3),在
t
<0时,
u
C
(0
-
)=
U
0
,在
t
=0时发生换路,根据换路定则,
u
C
(0
+
)=
U
0
,在
t
>0时,电容通过电阻放电,至电容电压为零,即
u
C
(∞)=0。戴维南等效电阻
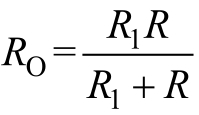 ,
τ
=
R
O
C
,则得到图2.4.1(b)所示电路的零输入响应为
,
τ
=
R
O
C
,则得到图2.4.1(b)所示电路的零输入响应为
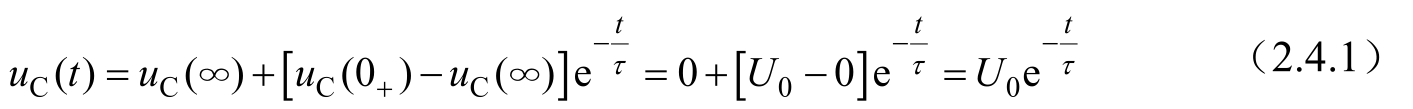
计算电流 i
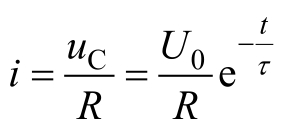
电压 u C ( t )的衰减快慢取决于时间常数 τ 。表2.4.1所示为不同时刻 t 对应的 u C 的数值。
表2.4.1 u C随时间衰减进度
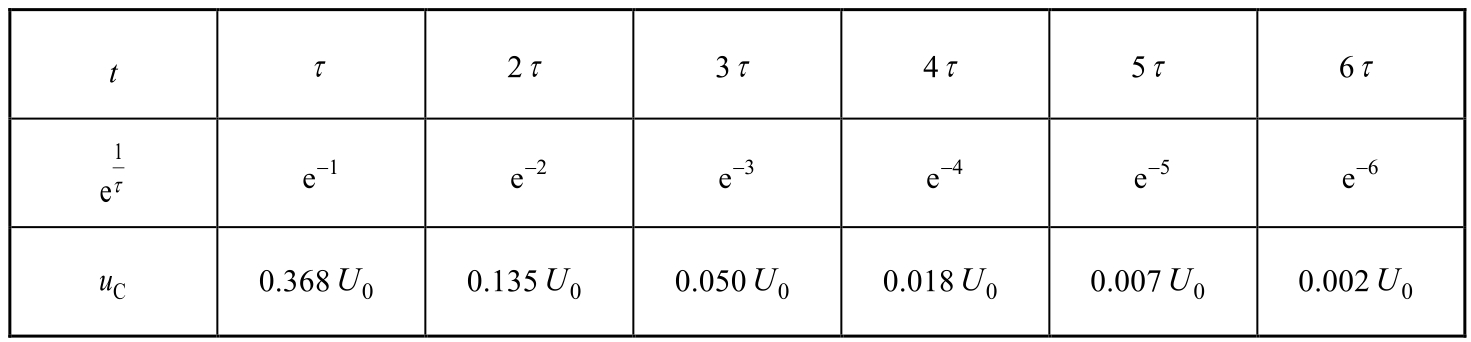
当 t =5 τ 时, u C (5 τ )=0.007 U 0 ,基本达到稳态值。工程上认为 t =(3~5) τ , u C 趋于 0,电容放电基本结束。
根据
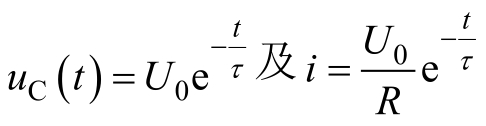 ,画出
u
C
、
i
的曲线,如图2.4.2所示。
,画出
u
C
、
i
的曲线,如图2.4.2所示。
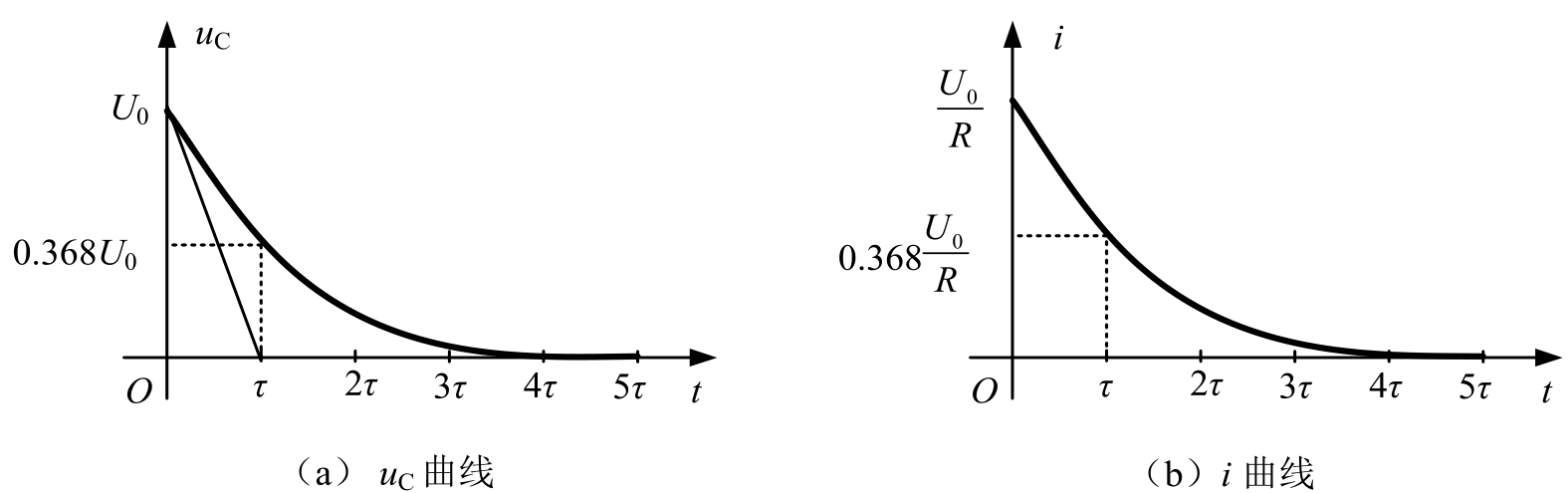
图2.4.2 一阶RC电路的零输入响应曲线
由此可见,时间常数 τ 等于电压 u C 衰减到初始值36.8%时所需的时间。此外,可以通过数学方法证明指数曲线上任意点的次切距的长度都等于 τ ,即过曲线上 t =0 处做曲线切线,则交横轴于 τ 。 τ 的大小取决于电路结构和元件参数,而与激励(外电源)无关。
从以上分析可知,RC 电路的零输入响应实际上是电容的放电过程,其物理意义是电容不断释放能量被电阻吸收,直到全部消耗完毕,使得原来存储在电容中的电场能全部被电阻吸收而转换成热能。
【例2.4.1】 电路如图2.4.3(a)所示,换路前电路处于稳定状态。 t =0时刻开关断开,求 t >0的电容电压和电容电流,指出属于什么响应并画出电容电压和电流波形图。
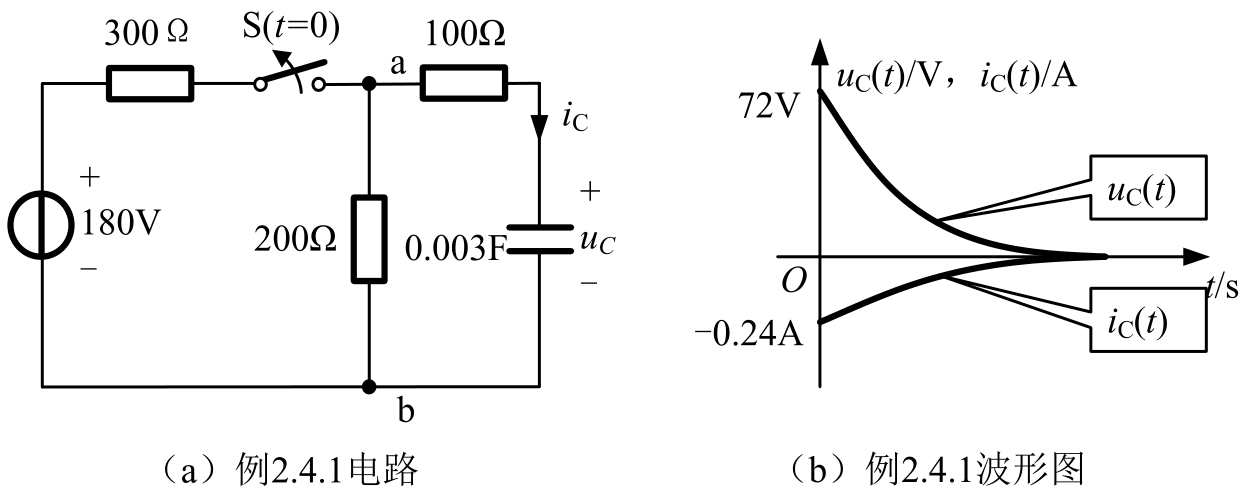
图2.4.3 例2.4.1电路及波形图
解: 此电路为一阶电路,适用三要素法求电压电流。
(1)求初始值。
换路前开关闭合,电路处于稳定状态,电容开路,其电流为零,电压等于 200Ω 电阻的电压,由此得到
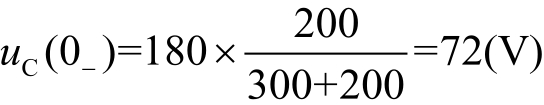
根据换路定则——容压感流, u C (0 + )= u C (0 - )=72(V)。
(2)求稳态值。
电容放电完毕后,电容的电压为0V,所以 u C (∞)=0(V)。
(3)求时间常数。
换路完成后电容两端看进去的戴维南等效电阻 R O 为
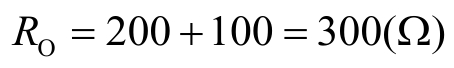
时间常数 τ = R O C =300×0.003=0.9 (s)。
(4)用三要素法公式求得。
将三要素代入式(2.3.3),得
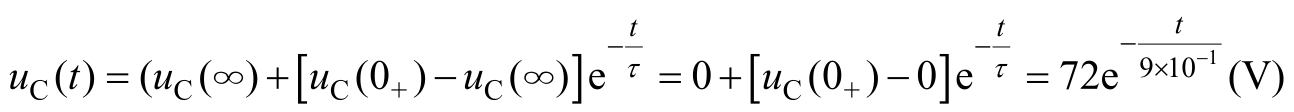
(5)求电容电流。
方法一:利用式(2.1.2)求电容电流
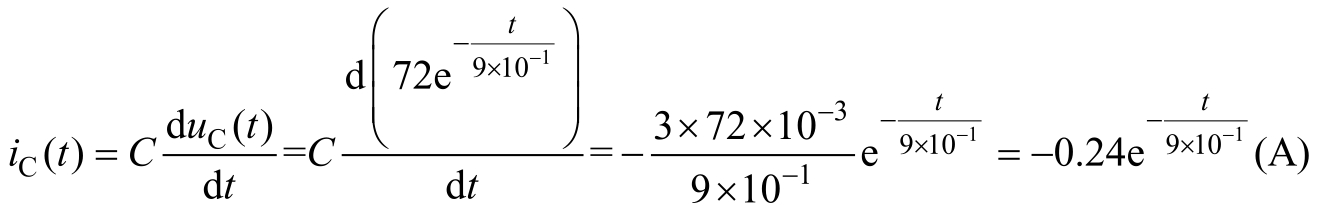
方法二:
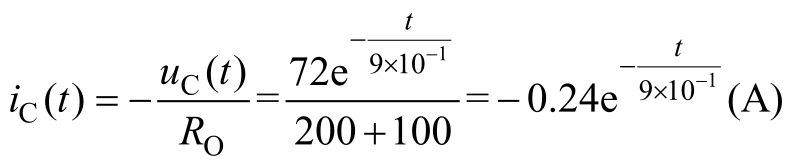
此电路为电容电压的零输入响应。波形图如图2.4.3(b)所示,电容放电至结束。
2.RL电路的零输入响应
以图2.4.4所示电路为例来说明RL电路零输入响应的计算过程。开关在1处时,如图2.4.4(a)所示,电感由电压源 U 0 充电。开关换路在2处时,电路如图2.4.4(b)所示,电感脱离电压源而与电阻 R 连接,此时无信号源作用,称为零输入响应。
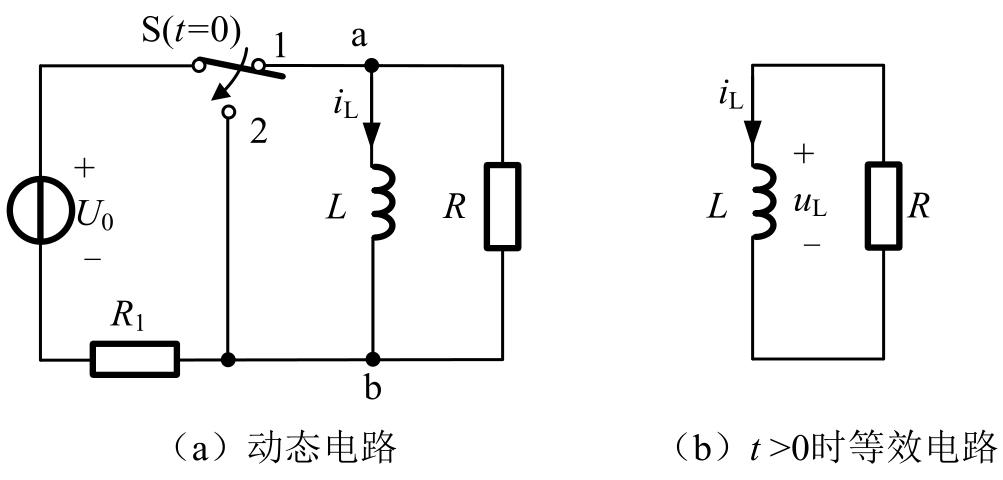
图2.4.4 RL电路的零输入响应
根据三要素式(2.3.3),在
t
<0时,电感储存一定的磁场能量,
i
L
(0
-
)=
I
0
,其中
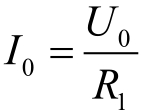 ,在
t
=0时开关S由1端倒向2端,发生换路,如图2.4.4(b)所示,根据换路定则,
i
L
(0
+
)=
I
0
,在
t
>0时,电感通过电阻放电,至电感电流为零,即
i
L
(∞)=0。戴维南等效电阻
R
O
=
R
,
,在
t
=0时开关S由1端倒向2端,发生换路,如图2.4.4(b)所示,根据换路定则,
i
L
(0
+
)=
I
0
,在
t
>0时,电感通过电阻放电,至电感电流为零,即
i
L
(∞)=0。戴维南等效电阻
R
O
=
R
,
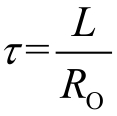 ,则得到图2.4.4(b)所示的RL零输入响应为
,则得到图2.4.4(b)所示的RL零输入响应为
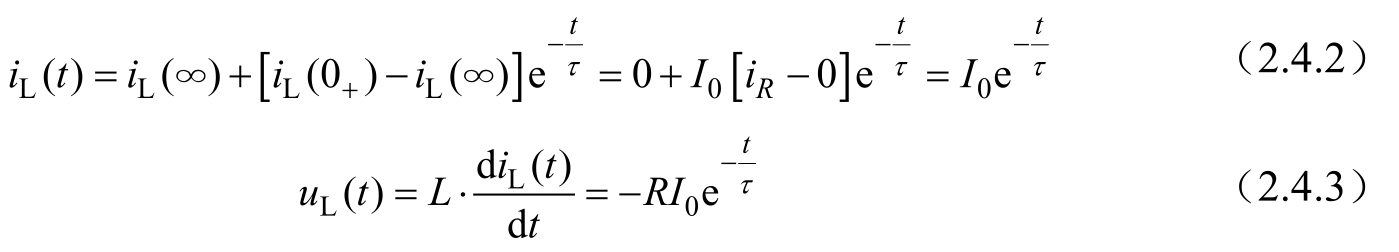
综上所述,图2.4.4(b)所示RL电路是电感 L 的初始储能逐渐释放出来消耗在电阻中的过程。
RL电路零输入响应波形如图2.4.5所示。图2.4.5(a)所示是电流从初始值,逐渐减小到零的过程,图 2.4.5(b)所示是电压从初始值,逐渐减小到零的过程。由零输入响应的波形及数学表达式可以看出,RL电路与RC电路都是从初始值开始按指数规律衰减的,衰减的快慢取决于时间常数 τ 。
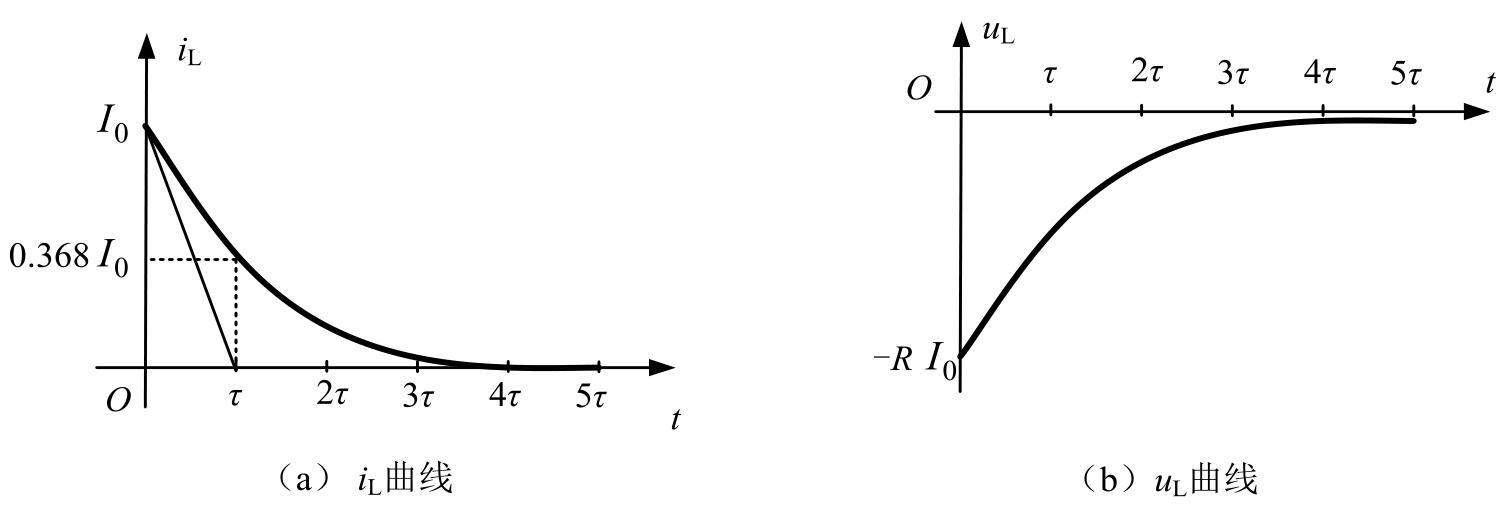
图2.4.5 RL电路零输入响应波形
【例2.4.2】 电路如图2.4.6(a)所示,换路前开关S处于1端,电路处于稳态。 t =0时开关S由1端合向2端,求换路后的 i L ( t )和 u L ( t ),指出属于什么响应并画出电感电压和电流波形图。(注:本书中有数值的,就给出了单位。)
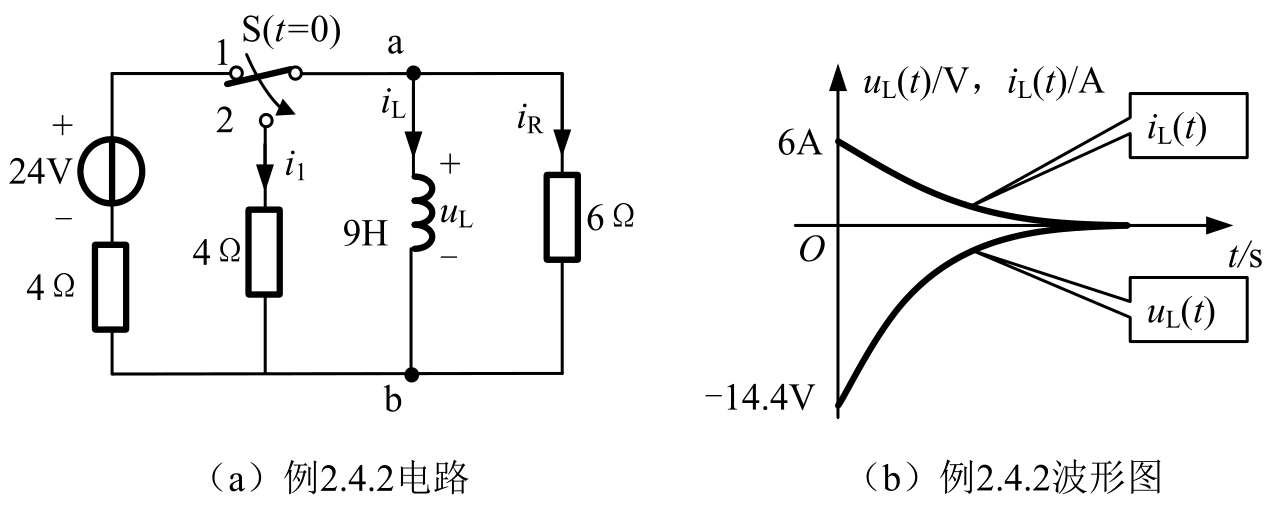
图2.4.6 例2.4.2电路及波形图
解: 此电路为一阶电路,适用三要素法求电压电流。
(1)求初始值。
换路前电路已稳定,电感相当于短路,
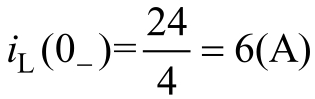 。
。
由换路定则——容压感流,可得 i L (0 + )= i L (0 - )=6(A)。
(2)求稳态值。
开关在2端,电感放电完毕后,电感的电流为0A,所以 i L (∞)=0(A)。
(3)求时间常数。
换路完成后从电感两端看进去的戴维南等效电阻 R O 为
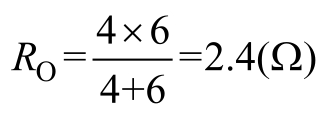
时间常数为
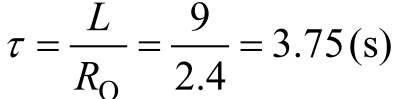 。
。
(4)用三要素法公式求解。
将三要素代入式(2.3.3),求得电感电流的零输入响应为
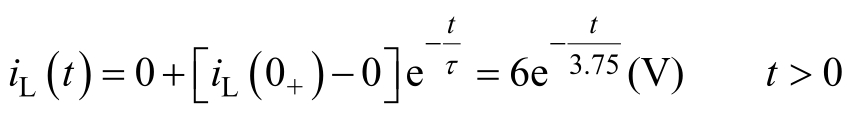
(5)电感电压。
方法一:根据式(2.1.4),得
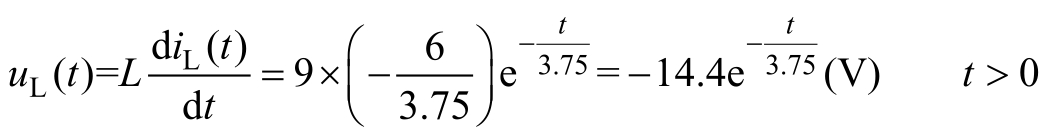
方法二:
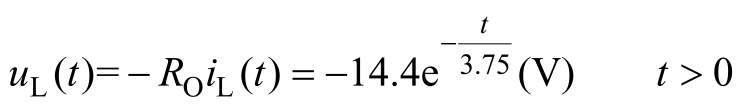
此电路为RL零输入响应。波形图如图2.4.6(b)所示,电感放电至结束。
一阶电路的初始状态为零,即 u C (0 + )=0或 i L (0 + )=0,由外加激励引起的响应,称为零状态响应(Zero-State Response)。
1.RC电路的零状态响应
如图2.4.7(a)所示电路,根据三要素式(2.3.3),在 t <0时,电容没有能量, u C (0 - )=0。在 t =0时开关S由1端转向2端,电压源 U S 接入RC电路发生换路,如图2.4.7(b)所示,根据换路定则, u C (0 - )= u C (0 + )=0,此刻电容电压为零,即换路瞬间电容短路。在 t >0时,电容通过电压源 U S 充电,至电容电压为 U S ,即 u C (∞)= U S 。戴维南等效电阻 R O = R 1 , τ = R 1 C ,则得到RC零状态响应电路为
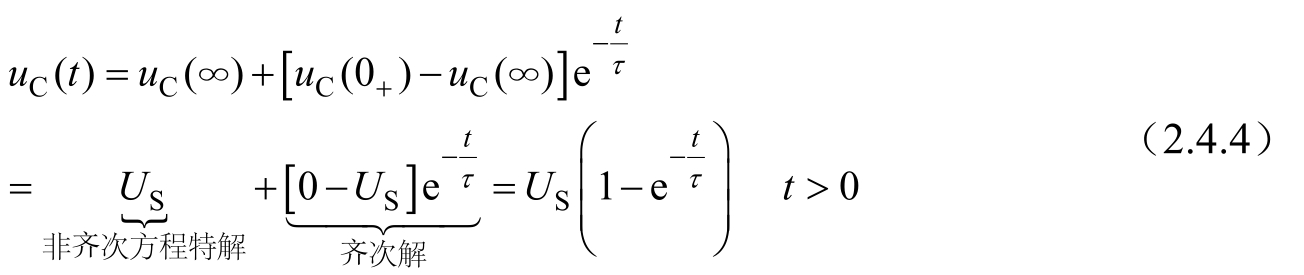
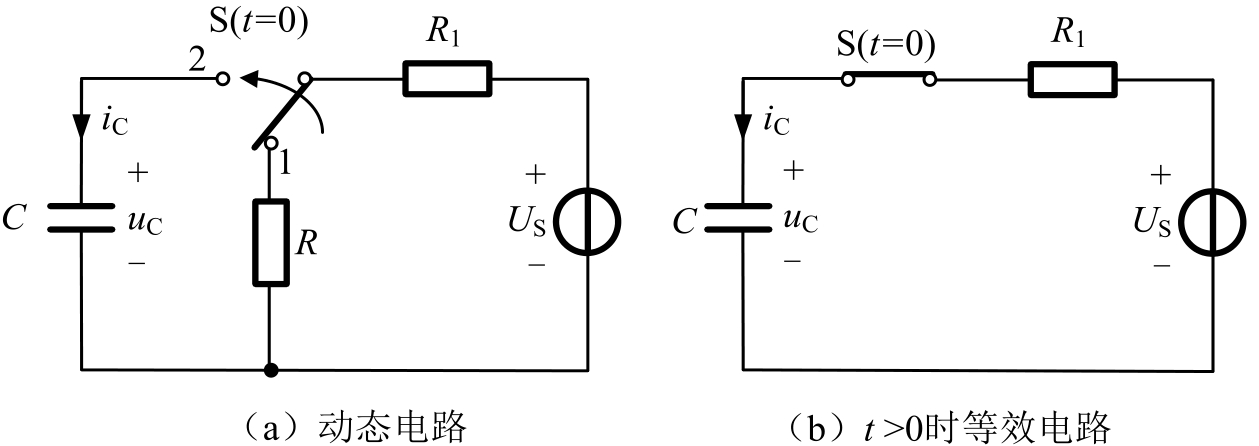
图2.4.7 RC电路的零状态响应
电容电流可以由电容伏安关系式(2.1.1)求得
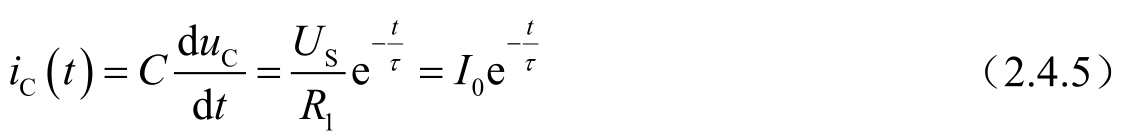
由式(2.4.4)可知,电容电压由两部分组成:第一部分是非齐次方程的特解
U
S
,与激励源形式相同的部分则称为“稳态响应分量”或“强制响应分量”;第二部分是对应的齐次微分方程的解
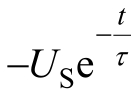 ,将随着时间的推移而逐渐地衰减为零,因此往往又把这一部分称为响应的“暂态响应分量”或“自由响应分量”。
,将随着时间的推移而逐渐地衰减为零,因此往往又把这一部分称为响应的“暂态响应分量”或“自由响应分量”。
RC电路的零状态响应曲线如图2.4.8所示。
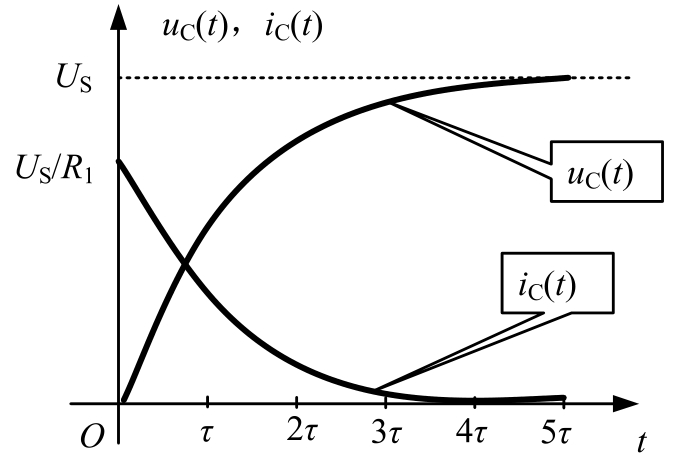
图2.4.8 RC电路的零状态响应曲线
在 RC 零状态电路的换路初始时刻,根据换路定则——容压感流,电容的电压为零,即电容短路,则电阻两端的电压为
U
S
,使电容电流由零跃变到
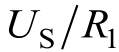 。随着时间
t
增加,电容的电压按指数规律不断充电,而电流按指数规律减小。当
t
>5
τ
时,电容的电压达到稳定值
U
S
,电流降为零,所以RC电路的零状态响应是一个电容充电的过程。
。随着时间
t
增加,电容的电压按指数规律不断充电,而电流按指数规律减小。当
t
>5
τ
时,电容的电压达到稳定值
U
S
,电流降为零,所以RC电路的零状态响应是一个电容充电的过程。
【例2.4.3】 电路如图2.4.9(a)所示,已知电容电压 u C (0 - )=0V, t =0开关S闭合,求 t >0的电容电压 u C ( t )和电容电流 i C ( t )。
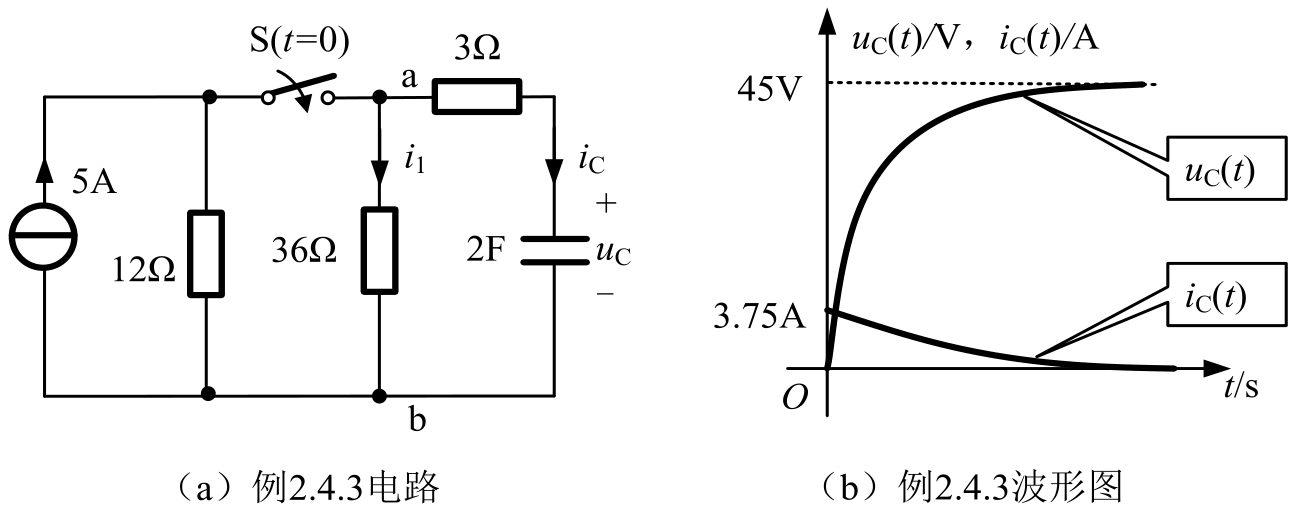
图2.4.9 例2.4.3电路及波形图
解: 此电路为一阶电路,适用三要素法求电压、电流。
(1)求初始值。
换路前电路已稳定,电容没有电流,其电压为0V,即 u C (0 - )=0(V)。
由换路定则——容压感流,可得 u C (0 + )= u C (0 - )=0(V)。
(2)求稳态值。
t
→∞时电容充电完毕后,电容相当于开路,电容两端的电压相当于36Ω电阻的电压,由此得到,
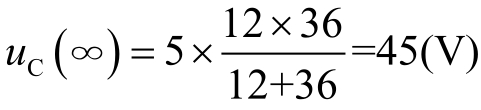 。
。
(3)求时间常数。
换路完成后从电容两端看进去的戴维南等效电阻 R O 为
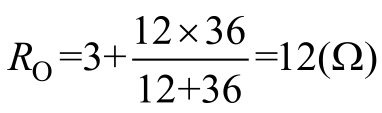
时间常数为 τ = R O C =12×2=24(s)
(4)用三要素法公式求解。
将三要素代入式(2.3.3),求得电感电流的零输入响应为
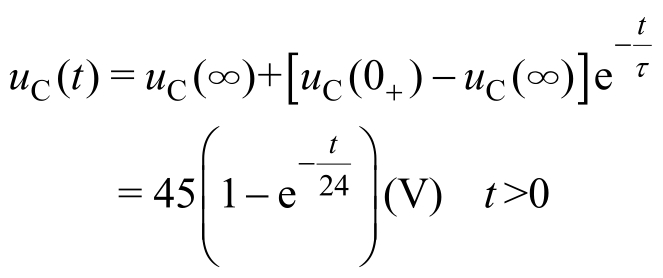
按式(2.1.1)可以得到电容电流
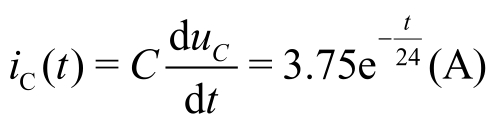
此电路为RC零状态响应。波形图如图2.4.9(b)所示。
2.RL电路的零状态响应
RL电路的零状态响应与RC电路的零状态响应相似,电路如图2.4.10所示。
根据三要素式(2.3.3),在
t
<0时,电感没有能量,
f
(0
-
)=0,在
t
=0时开关S由1端转向2端,电压源
U
S
接入RL电路发生换路,如图2.4.10所示,根据换路定则,
f
(0
+
)=0,在
t
>0时,电感通过电压源
U
S
充电,至电感电流为
U
S
/
R
,即
i
L
(∞)=
U
S
/
R
。戴维南等效电阻
R
O
=
R
,
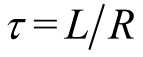 ,则得到RL零状态响应电路为
,则得到RL零状态响应电路为
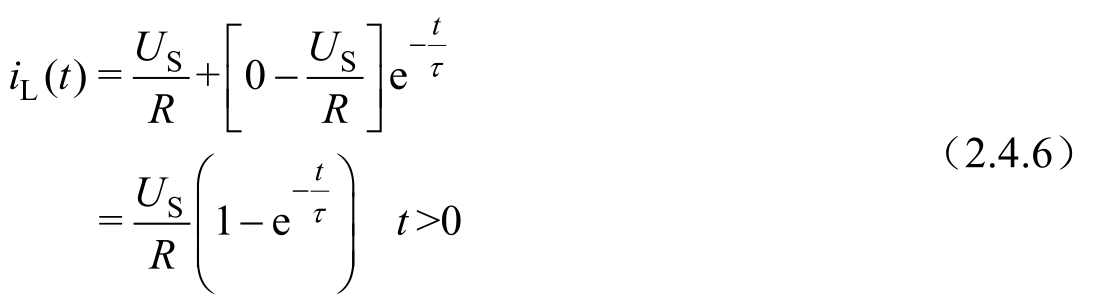
根据式(2.1.4),得
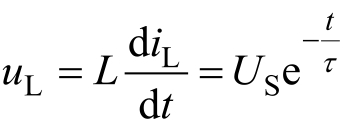 。
。
RL电路的零状态响应曲线如图2.4.11所示。(注:本书中没有具体数值的,就没有给单位;有具体数值的,就给出单位。)
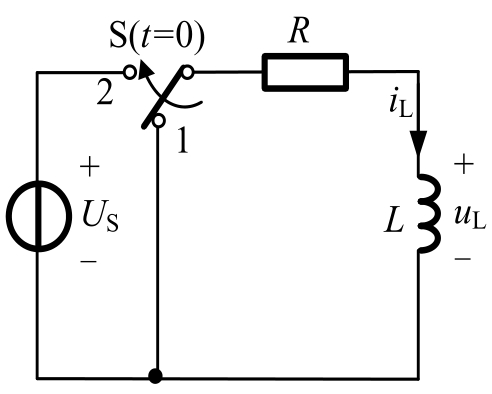
图2.4.10 RL电路的零状态响应
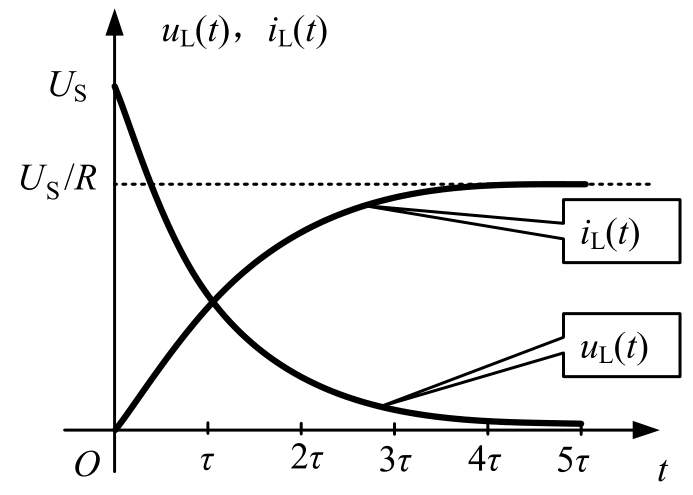
图2.4.11 RL电路的零状态响应曲线
一阶电路的零状态响应是动态元件在直流电源作用下储存能量的过程,动态元件的状态变量由初始值 0,按指数规律逐渐上升,最后达到稳态值。直流电源供给的能量一部分被电阻所消耗,一部分被动态元件转换为电场/磁场能储存起来。
零状态响应具有线性特性,即多个外加激励电源作用于初始状态为零的电路时,其零状态响应可以进行线性叠加,这种外加激励与零状态响应之间的正比关系称为零状态比例性。
【例2.4.4】 电路如图2.4.12(a)所示,已知电感电流 i L (0 - )=0A, t =0闭合开关S,求 t >0的电感电流 i L ( t )和电感电压 u L ( t )。
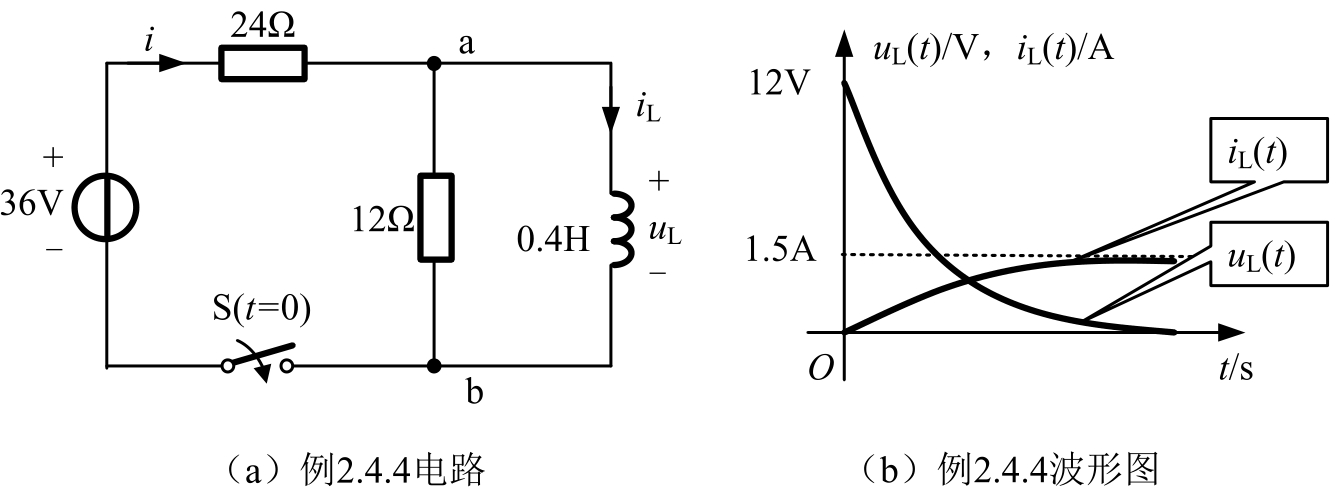
图2.4.12 例2.4.4电路及波形图
解: 此电路为一阶电路,适用三要素法求电压、电流。
(1)求初始值。
换路前电路已稳定,电感上没有电流,即 i L (0 - )=0(A)。
由换路定则——容压感流,可得 i L (0 + )= i L (0 - )=0(A)。
(2)求稳态值。
电感充电完毕后,电感相当于短路,注意电流不流经12Ω电阻,所以
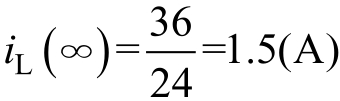 。
。
(3)求时间常数。
换路完成后从电感两端看进去的戴维南等效电阻 R O 为
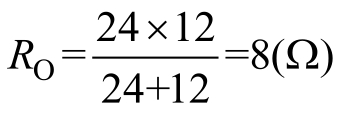
时间常数为
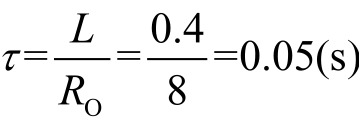 。
。
(4)用三要素法公式求解。
将三要素代入式(2.3.3),求得电感电流的零输入响应为
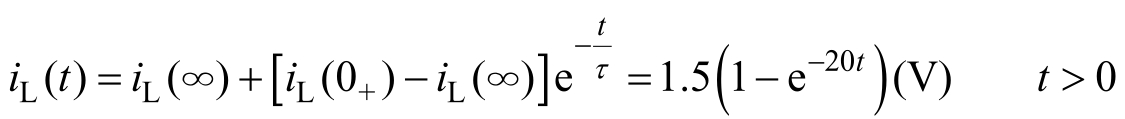
电感电压根据式(2.1.4),得
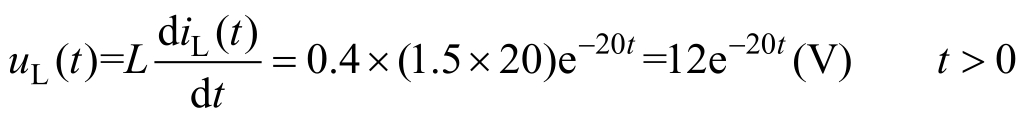
此电路为RL零输入响应。
式(2.3.3)又可写成
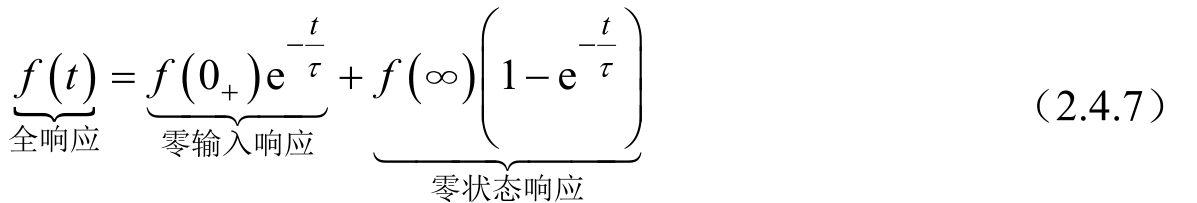
式(2.4.6)中等式右边第一项是零输入响应,第二项是零状态响应,这表明全响应为零输入响应与零状态响应的线性叠加,这是叠加定理在线性动态电路分析中的体现,这种分解方式强调外加激励与响应的因果关系。
三种响应的曲线如图2.4.13所示,零输入响应是初始状态的线性函数,零状态响应是外加激励的线性函数,全响应既不是激励的线性函数,也不是初始状态的线性函数,因此全响应不具有比例性。
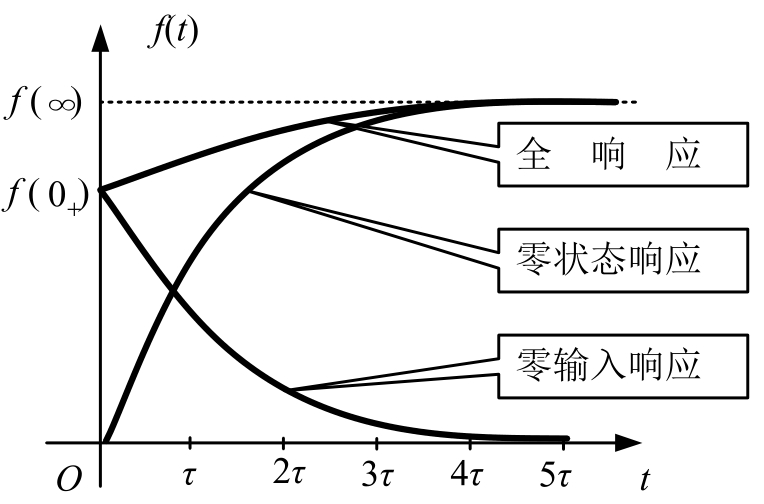
图2.4.13 三种响应的曲线
【例2.4.5】 电路如图2.4.14(a)所示,已知 u C (0 - )=-5V, t =0闭合开关S,求 t >0的电容电压 u C ( t )和电流 i ( t ),并画出电容电压 u C ( t )和电流 i ( t )响应曲线。
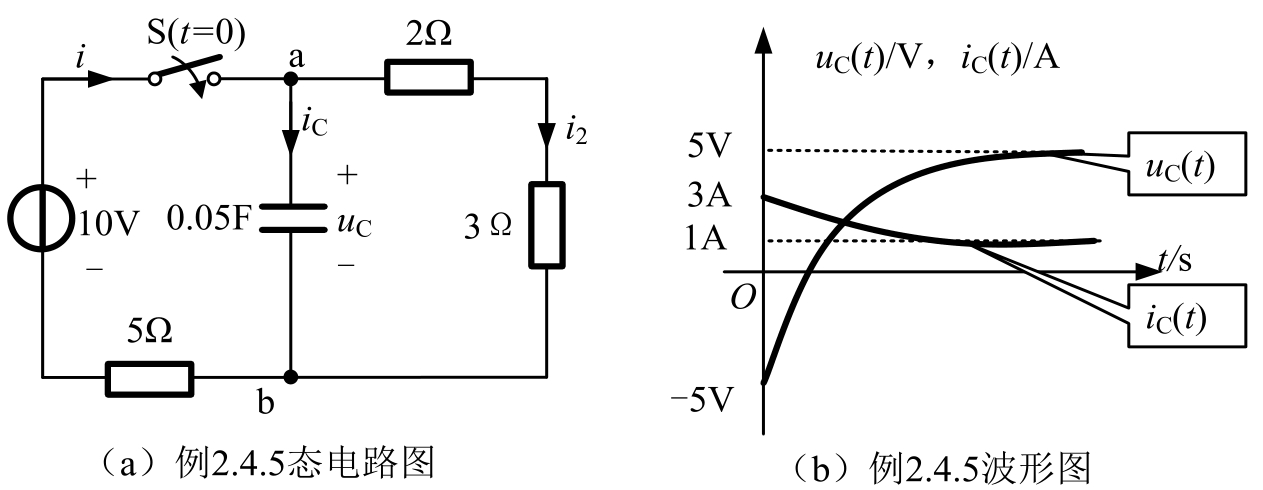
图2.4.14 例2.4.5电路及波形图
解: 由于在开关S闭合前,电容已有电压,即电容状态不为0,开关S闭合后,在 t →∞时电容电压是两电阻串联电压,因此电容先是放电再充电,这个过程是全响应。适用三要素法求元件的电压电流。
(1)求初始值 f (0 + )。
根据题意 t =0 - 时的电容电压初始值 u C (0 - )=-5(V)。
根据换路定则, u C (0 + )= u C (0 - )=-5(V)。
(2)求稳态值 f (∞)。
t →∞时电容用开路代替或电感用短路代替,得到一个直流等效电路,电容电压是两电阻串联电压,即
稳态值 u C (∞)=5(V)。
(3)求时间常数 τ 。
① 戴维南等效电阻 R O 。
在
t
→∞时的等效电路中,断开电容,将所有的独立电源置零(电压源短路,电流开路)后,从电容两端看进去,
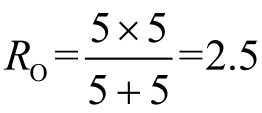 。
。
② 时间常数 τ 。
τ = R O C =2.5×0.05=0.125(s).
(4)求一阶电路响应 f ( t )。
利用三要素法式(2.3.3)得
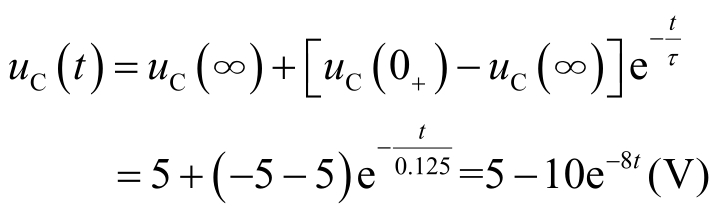
(5)电阻上的电流 i ( t )。
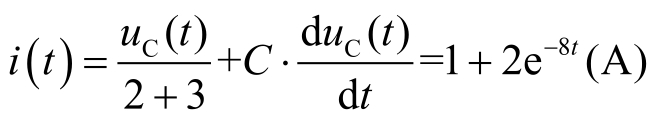
波形如图2.4.14(b)所示,电容是先放电再充电。
【例2.4.6】 电路如图2.4.15(a)所示, t >0时,开关S 1 断开,开关S 2 处于1端,电路已处于稳态,电容未储能, t =0时开关S 1 闭合, t =1s时,开关S 2 由1端转到2端,试分析电感电流的 i L 变化规律及响应变化情况。
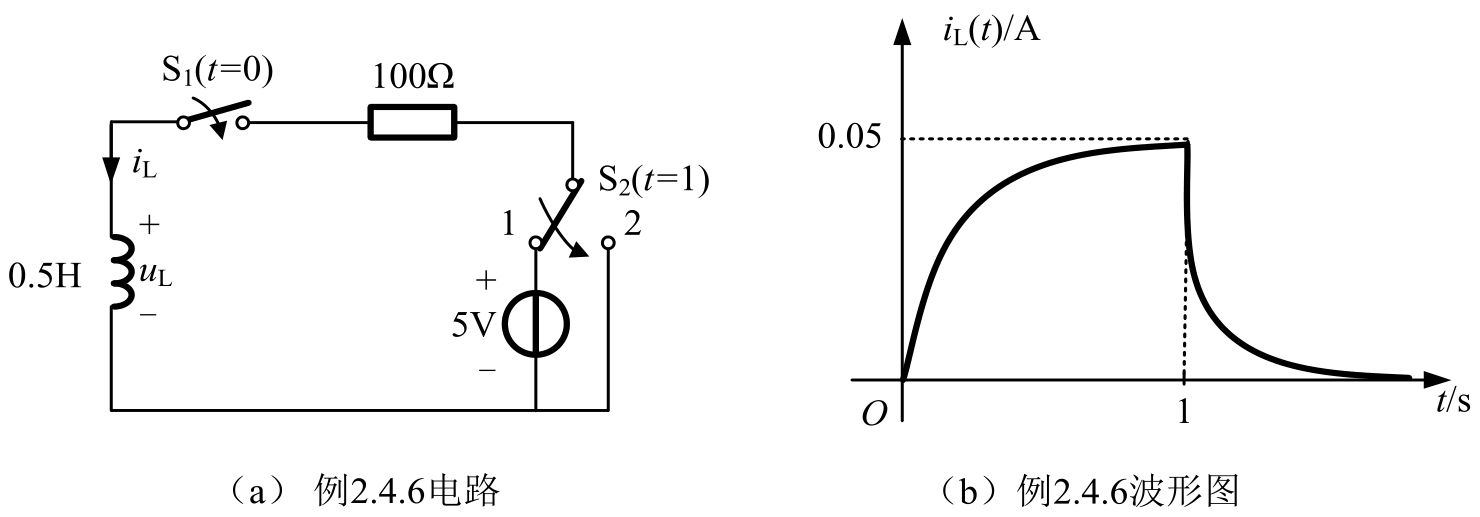
图2.4.15 例2.4.6电路及波形图
解: 此题电感先进行充电,再进行放电,所以分两部分分析。
(1)在0< t <1 期间电感充电至结束。
① 求初始值。
开关S 1 闭合,电感开始充电, i L (0 - )=0(A),根据换路定则——容压感流,得 i L (0 + )= i L (0 - )=0(A)。
② 求稳态值。
电感充电结束,此时电感相当于短路,
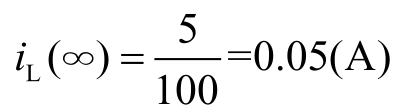 。
。
③ 求时间常数。
换路完成后从电感两端看进去的等效电阻
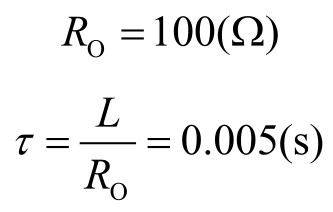
④ 用三要素式求解。
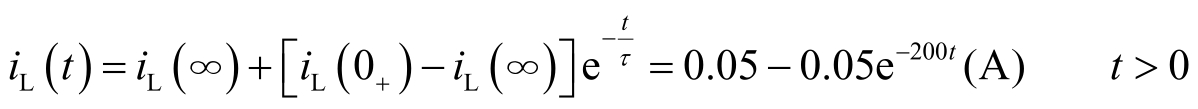
由于 τ ≪1s,所以电感很快从0A充电到0.05A。
(2)在 t >1期间,开关S 2 闭合,电感放电至结束。
① 求初始值。
开关 S 2 闭合,电感开始放电, i L (0 - )=0.05(A),据换路定则——容压感流,得 i L (0 + )= i L (0 - )=0.05(A)。
② 求稳态值。
电感放电结束, i L (∞)=0(A)。
③ 求时间常数。
换路完成后从电感两端看进去的等效电阻
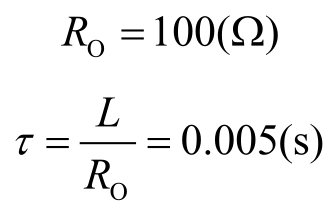
④ 用三要素式求解。
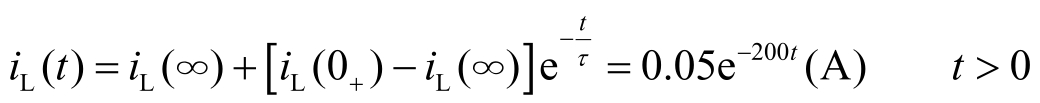
由于 τ ≪1s,所以电感很快从0.05A放电到0A。整个过程波形如图2.4.15(b)所示。