





有了这些工具,我们现在就可以开始进行第一个真正的分类示例了。
以兰普威尔小镇为例,那里的人们为他们的两支球队——兰普威尔红队和兰普威尔蓝队——而疯狂。红队已经存在很长时间了,人们很喜欢这支队伍。但是后来,一些外地来的富翁买下了红队的最佳射手,成立了一支新的球队——蓝队。令多数红队球迷不满的是,这位最佳射手将继续带领蓝队夺得冠军。多年后,尽管一些球迷对他早期的职业选择强烈不满,但他还是回到了红队。可是不管怎么说,你会明白为什么红队的球迷和蓝队的球迷一直不能和睦相处。事实上,这两队的球迷是如此分裂,以至于他们从未在同一处居住过。我们甚至听说过这样的故事:当蓝队球迷搬到隔壁时,红队球迷就会故意离开。故事是真实的!
不管怎样,我们是新到镇上的,我们正挨家挨户向人们推销蓝队产品。然而,我们偶尔会遇到心在滴血的红队球迷因为我们推销蓝队的东西而对我们大吼大叫,还把我们赶出他们的草坪。太不友好了!完全避开这些红队球迷,而只拜访蓝队球迷,这样压力会小很多,我们的时间也能更好地被利用。
我们相信可以预测红队球迷的生活区,开始记录我们的活动轨迹。如果我们路过红队球迷的家,则会在手边的城镇地图上画一个红色的三角形;否则会画一个蓝色的正方形。一段时间后,我们对每个人的居住地有了一个很好的了解,如图3-3所示。
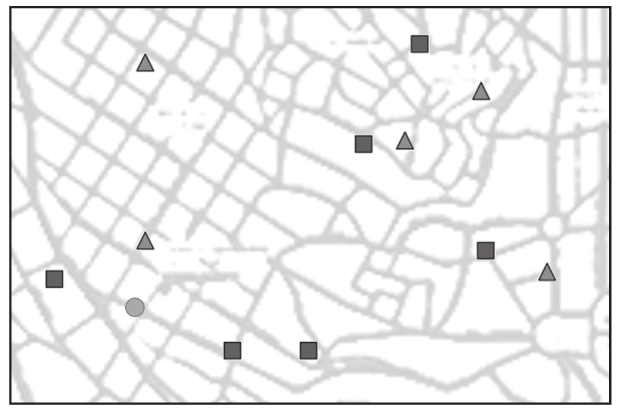
图3-3 在地图中用不同颜色标记红队和蓝队球迷居住地
可是,在图3-3中,我们正在靠近一间标记为绿色圆圈的房子。我们应该敲他们的门吗?我们试图找到一些线索,以确定他们可能是哪个队的球迷(也许在后门廊上挂着队旗,可我们没看到)。我们怎样才能知道敲他们的门是安全的呢?
这个例子恰恰描述了监督学习算法可以解决的问题。我们有一堆观测数据(房子、位置以及颜色),这些数据构成了我们的训练数据。我们可以利用这些数据从经验中学习,当我们要对一个新房子进行颜色预测的任务时,我们就可以做出明智的估计。
正如前面说过的那样,红队球迷对他们的球队充满感情,所以他们永远不会和蓝队球迷住在一起。我们能不能利用这些信息,观察一下周围的房子,再看看新房子里住的是哪个队的球迷?
这正是k-NN算法能够实现的。
k-NN算法可以说是机器学习算法中最简单的一个。原因是我们基本上只需要存储训练数据集。然后,要预测一个新的数据点,我们只需要找到训练数据集中最近的数据点:它的最近邻居。
简而言之,k-NN算法认为一个数据点可能与其邻居属于同一类。想想看,如果我们的邻居是红队球迷,我们可能也是红队球迷;否则,我们早就搬走了。对于蓝队球迷来说也是如此。
当然,有些邻居可能稍微有点复杂。在这种情况下,我们可能不只要考虑我们的最近邻居(k=1),而且还要考虑离我们最近的k个最近邻居。让我们继续前面介绍过的例子,如果我们是红队球迷,我们不可能搬到大多数人都认为可能是蓝队球迷的社区。
这就是它的全部。
使用OpenCV,通过cv2.ml.KNearest_Create()函数我们可以很容易创建一个k-NN模型。构建模型包括下列步骤:
1)生成一些训练数据。
2)对于一个给定的数k,创建一个k-NN对象。
3)为我们要分类的一个新数据点找到k个最近邻。
4)根据多数票分配新数据点的类标签。
5)绘制结果。
首先,我们导入所有必要的模块:OpenCV的k-NN算法模块、NumPy的数据处理模块、Matplotlib的绘图模块。如果你正在使用Jupyter Notebook,请不要忘记调用%matplotlib inline魔术命令:

第一步是生成一些训练数据。为此,我们将使用NumPy的随机数生成器。正如3.2节讨论过的,我们将固定随机数生成器的种子,这样重新运行脚本总是可以生成相同的值:

好了,现在让我们开始吧。我们的训练数据应该是什么样子的呢?
在前面的例子中,每个数据点都是城镇地图上的一个房子。每个数据点都有两个特征(即数据点在城镇地图上的位置坐标x和y)以及一个类标签(即蓝队球迷居住地是一个蓝色方块,红队球迷居住地是一个红色三角形)。
因此,单个数据点的特征在城镇地图上可以用x和y坐标的一个二元向量来表示。类似地,如果是一个蓝色方块,那么标签是0;如果是一个红色三角形,那么标签是1。这个过程包括数据点生成、数据点绘制以及新数据点的标签预测。让我们来看看如何实现这些步骤:
1)随机选择地图上的位置以及一个随机标签(0或者1),我们可以生成单个数据点。假设城镇地图的范围是0≤x≤100和0≤y≤100。那么,我们可以生成一个随机数据点,如下所示:

在上述输出中我们可以看到,这将在0到100之间选择两个随机整数。我们把第一个整数解释为地图上数据点的x坐标,第二个整数解释为数据点的y坐标。
2)类似地,我们为数据点选择一个标签:
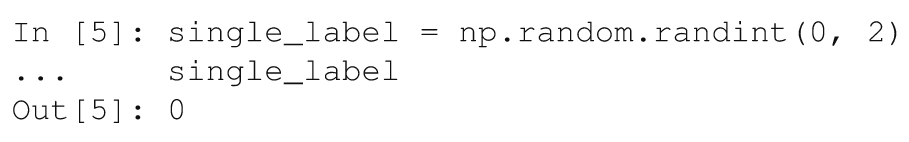
这个数据点的类是0,将其解释为一个蓝色方块。
3)让我们将这个过程封装到一个函数中,该函数以生成的数据点数(即num_samples)和每个数据点的特征数(即num_features)作为输入:

因为在我们的例子中,特征数是2,所以可以使用这个数作为默认的参数值。这样,如果我们在调用函数时,没有显式地指定num_features,那么会将一个为2的值自动分配该函数。我相信你现在已经明白了。
我们要创建的数据矩阵应该有num_samples行num_features列,而且矩阵中的每个元素都应该是从(0, 100)范围内随机选取的一个整数:

类似地,我们要创建一个向量,包含(0, 2)范围内的一个随机整数标签,对于所有样本:

不要忘记让函数返回生成的数据:
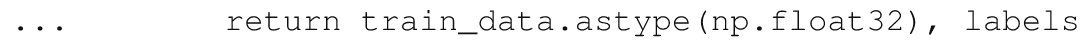
在涉及数据类型时,OpenCV可能有点挑剔,因此一定要将数据点转换成np.float32!
4)让我们对该函数进行测试并生成任意数量的数据点,假设为11个数据点,其坐标是随机选择的:

5)正如我们在上述输出中看到的那样,train_data变量是一个11×2的数组,每一行对应一个数据点。通过在数组中建立索引来查看第一个数据点及其对应的标签:

6)这就告诉我们第一个数据点是一个红色三角形(因为它的类是1),在城镇地图上的位置是(x, y)=(71, 60)。如果需要,我们可以使用Matplotlib绘制城镇地图上的这个数据点:

我们得到的结果如图3-4所示。
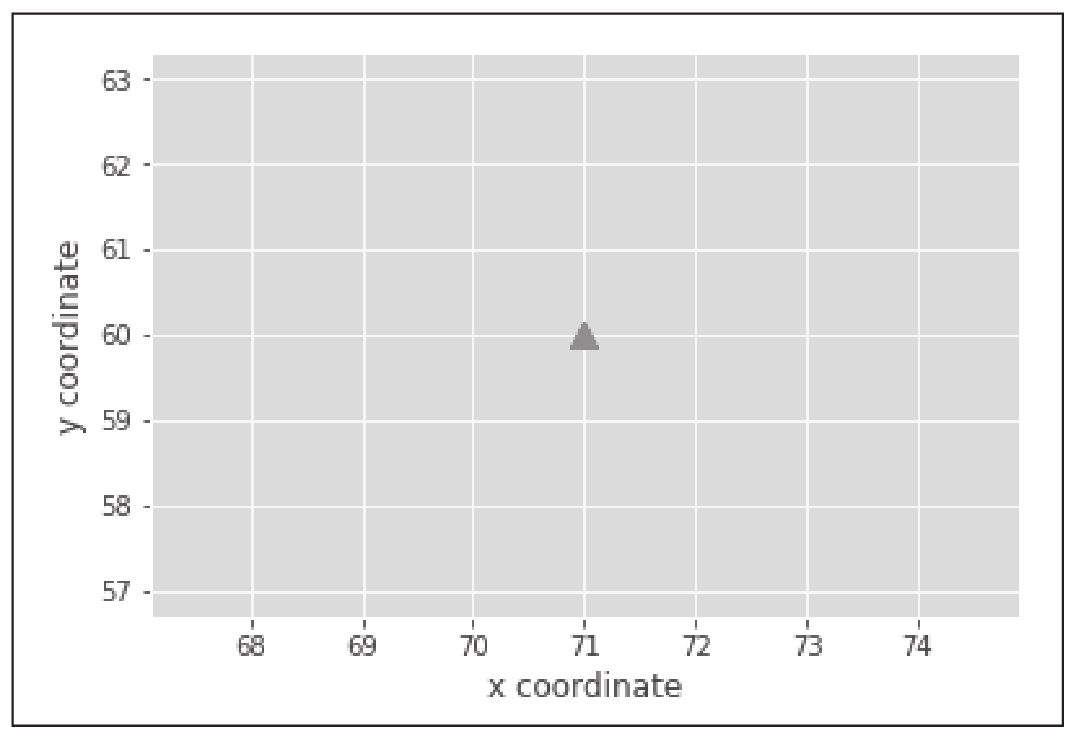
图3-4 生成第一个数据点及其标签
7)但是,如果我们想一次看到整个训练集呢?让我们为此编写一个函数。应该把所有蓝色方块数据点的列表(all_blue)以及所有红色三角形数据点的列表(all_red)作为函数的输入:

8)我们的函数应该把所有的蓝色数据点绘制成蓝色方块(使用颜色“b”和标记“s”),这可以使用matplotlib的scatter函数来实现。为了使其可以工作,我们必须以一个N×2的数组形式传递蓝色数据点,其中N是样本数。然后,all_blue [:, 0]包含数据点的所有x坐标,all_blue[:, 1]包含数据点的所有y坐标:

9)类似地,所有的红色数据点也可以这样实现:

10)最后,我们用标签标注图:
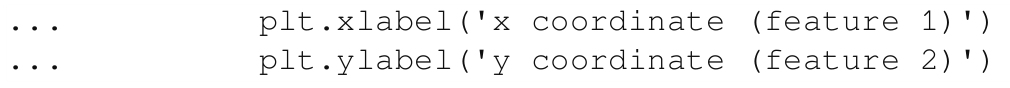
11)让我们在数据集上试试看!首先,我们必须将所有的数据点拆分成红色数据集和蓝色数据集。使用下列命令,我们可以快速选择前面创建的label数组中所有等于0的元素(ravel平展数组):

12)所有蓝色数据点是之前创建的train_data数组的所有行,对应的标签是0:

13)对于所有的红色数据点也可以这样实现:

14)最后,让我们绘制所有的数据点:
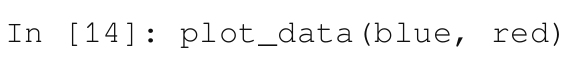
创建的图如图3-5所示。
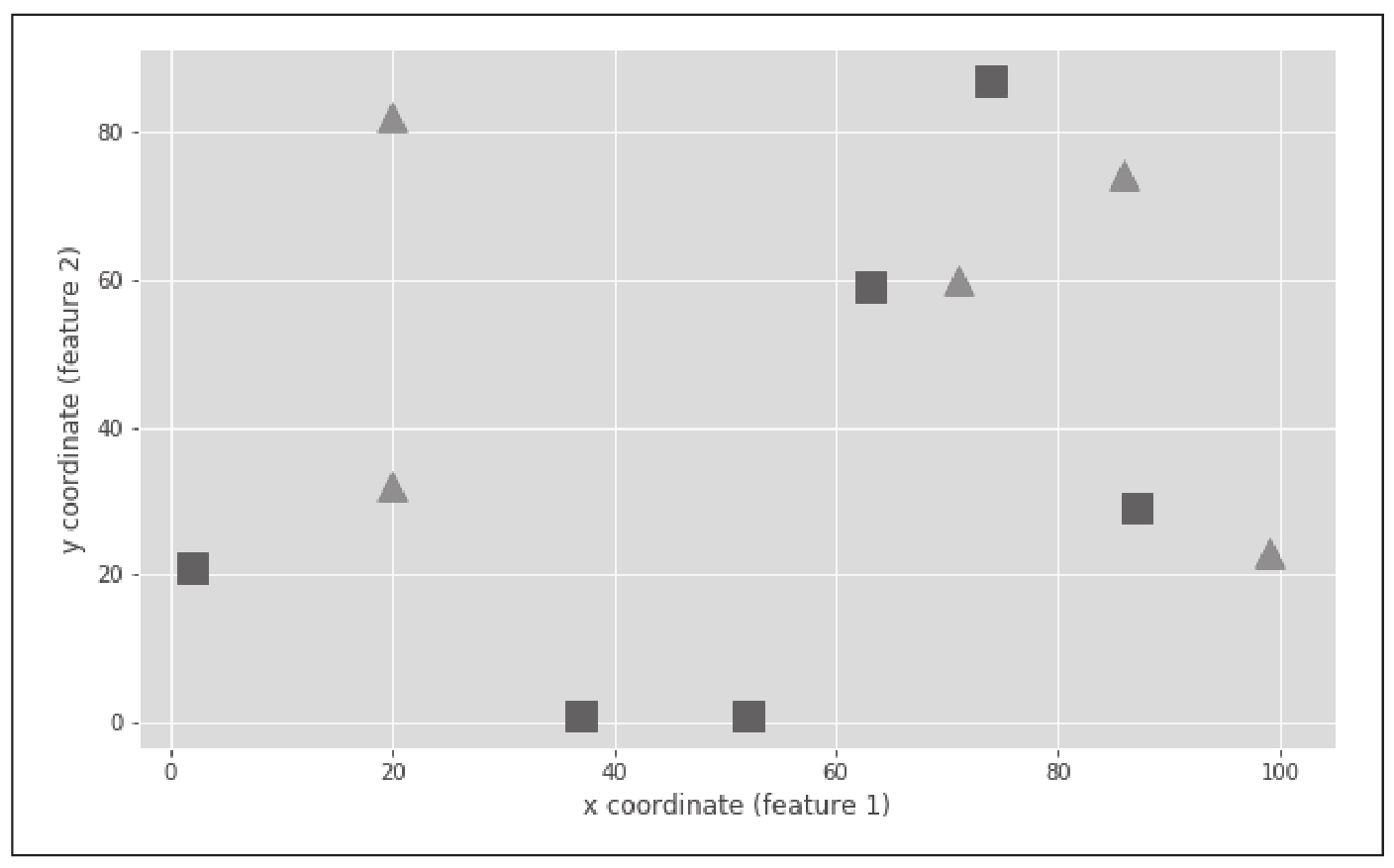
图3-5 生成所有数据点
现在是时候训练分类器了。
与机器学习的所有其他函数一样,k-NN分类器是OpenCV 3.1 ml模块的一部分。使用下列命令,我们可以创建一个新的分类器:
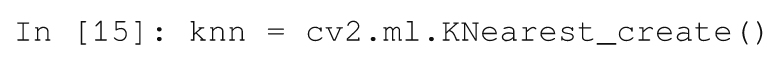
在OpenCV的老版本中,这个函数被称为cv2.KNearest( )。
然后,我们将训练数据传递给train方法:

此处,我们必须让knn知道我们的数据是一个N×2的数组(即每一行是一个数据点)。成功后,函数返回True。
knn提供的另一个非常有用的方法是findNearest。该方法可以基于其最近邻居预测一个新数据点的标签。
generate_data函数生成一个新的数据点实际上是很容易的!我们可以把一个新数据点看成大小为1的数据集:
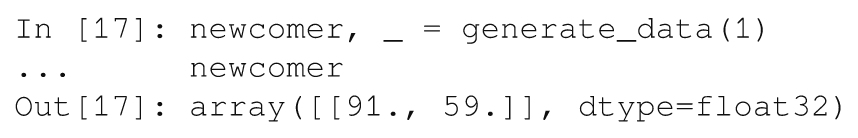
我们的函数还会返回一个随机标签,可是我们对此并不感兴趣。我们想用已训练的分类器来预测!我们可以让Python忽略一个带有下划线(_)的输出值。
让我们再来看看我们的城镇地图。我们将像前面那样绘制训练集,而且还将新数据点添加为一个绿色圆圈(因为我们还不知道这个数据点应该是蓝色方块还是红色三角形):

你可以向plt.plot函数调用添加一个分号来抑制其输出,与Matlab中的一样。
上述代码将生成图3-6(–环)。
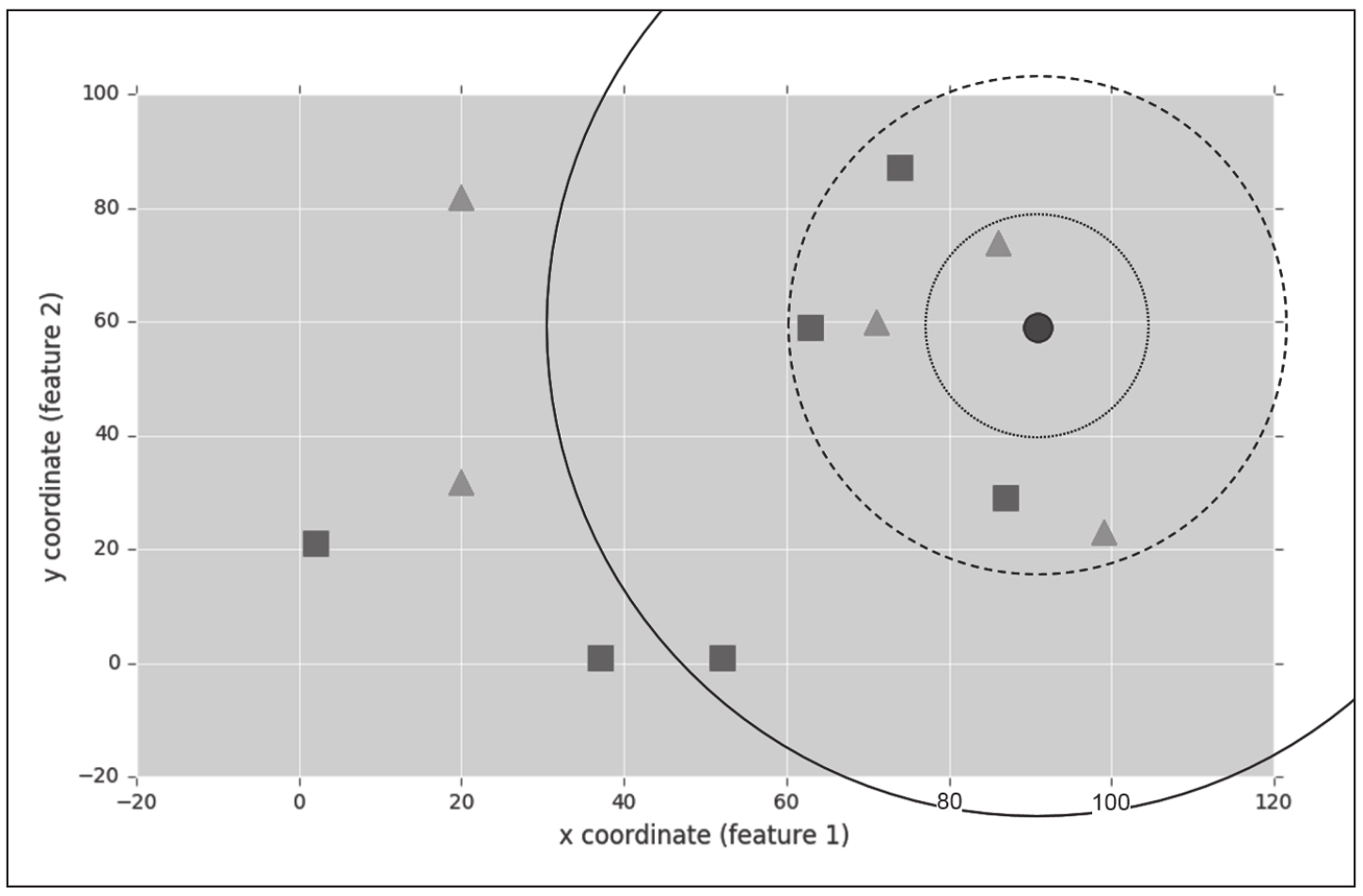
图3-6 生成的结果图
如果你必须根据该数据点的邻居来猜测的话,你会为新数据点分配什么标签?蓝色方块,还是红色三角形?
这要看情况,不是吗?如果我们查看离该点最近的房屋(大概在(x, y)=(85, 75),在图3-6中的虚线圆圈内),我们可能也会给新数据点分配一个三角形。这也正好是我们的分类器所预测的k=1:

这里,knn报告最近邻居是250个任意单位距离,这个邻居标签是1(我们说过它对应于红色三角形),因此,新数据点也应该标记为1。如果我们看看k=2的最近邻居和k=3的最近邻居,情况也是一样的。但我们要注意不要令k为偶数,这是为什么呢?在图3-6中(虚线圆圈)可以看到原因,在虚线圆圈内的6个最近邻居中,有3个蓝色方块,3个红色三角形——打平了!
在平局情况下,OpenCV的k-NN实现将更喜欢与数据点的总体距离更近的邻居。
最后,如果我们扩大搜索窗口,根据k=7的最近邻居对新数据点进行分类,结果会怎样呢(图3-6中的实线圆圈)?
我们通过调用findNearest方法、k=7的邻居找出答案:

此时,预测标签变成了0(蓝色方块)。原因是,现在我们在实线圆圈内有4个邻居是蓝色方块(标签0),只有3个邻居是红色三角形(标签1)。因此,多数票表明这个新数据点也应该是一个蓝色方块。
或者,可以使用predict方法进行预测。但是,首先我们需要设置k:

如果我们设置k=7会怎样呢?让我们来看看吧:

正如你所看到的,k-NN的结果随k值的变化而变化。但是,通常我们事先并不知道k取什么值最合适。对于这个问题,最简单的解决方案是尝试一系列k值,看看哪个值表现最佳。在本书的后续章节中,我们将学习更复杂的解决方案。