





1.理解空间直角坐标系的概念。
2.会用空间两点间的距离公式计算两点间的距离。
3.了解向量的概念,会求向量的模、单位向量、向量的方向余弦等。
【 定位问题 】一学生进入教学楼大门后向西走5 m,通过电梯到2楼,每层楼高约4 m,再向北走10 m,那么如何表示学生所在的位置?
在空间任取一点 O ,过点 O 作三条两两互相垂直且具有相同单位长度的数轴,分别称为 x 轴(横轴)、 y 轴(纵轴)、 z 轴(竖轴),统称为 坐标轴; 三轴的交点 O 称为 原点 ;任意两条坐标轴所确定的平面称为 坐标面 ,即 xOy , yOz , zOx 三个坐标面。
建立空间直角坐标系时,习惯上常把
x
轴、
y
轴置于水平面上,而
z
轴置于铅垂线上,各轴正向及顺序遵循右手法则,即用右手握住
z
轴,右手的四指从
x
轴正向以
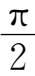 的角度转向
y
轴的正向时,大拇指的指向是
z
轴的正向,如图1-1所示。
的角度转向
y
轴的正向时,大拇指的指向是
z
轴的正向,如图1-1所示。
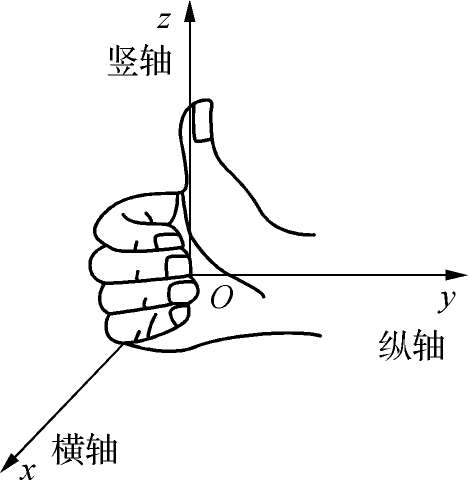
图1-1
三个坐标面又将空间分成八个部分,各部分依次称为第Ⅰ,Ⅱ,Ⅲ,Ⅳ,Ⅴ,Ⅵ,Ⅶ,Ⅷ卦限,如图1-2所示,坐标面是卦限的界面,不属于任何卦限。
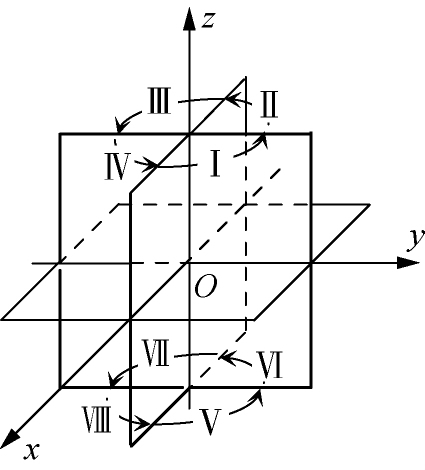
图1-2
设点 M 为空间的一点,过点 M 分别作与三条坐标轴垂直的平面,交点分别为 P , Q , R (如图1-3),这三点在坐标轴上的坐标依次为 x , y , z ,则空间的点 M 唯一确定了一个三元有序数组( x , y , z ).显然,空间的点 M 与有序数组( x , y , z )之间建立了一一对应关系。
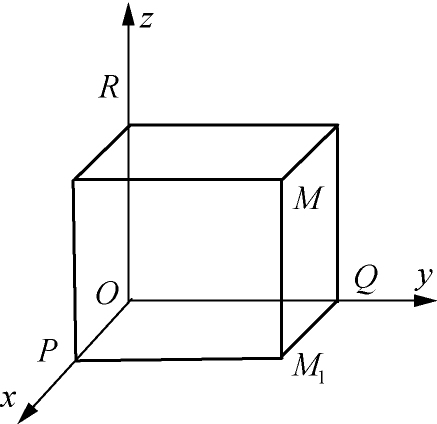
图1-3
空间直角坐标系中八个卦限上点的坐标特征列表如下(见表1-1):
表1-1
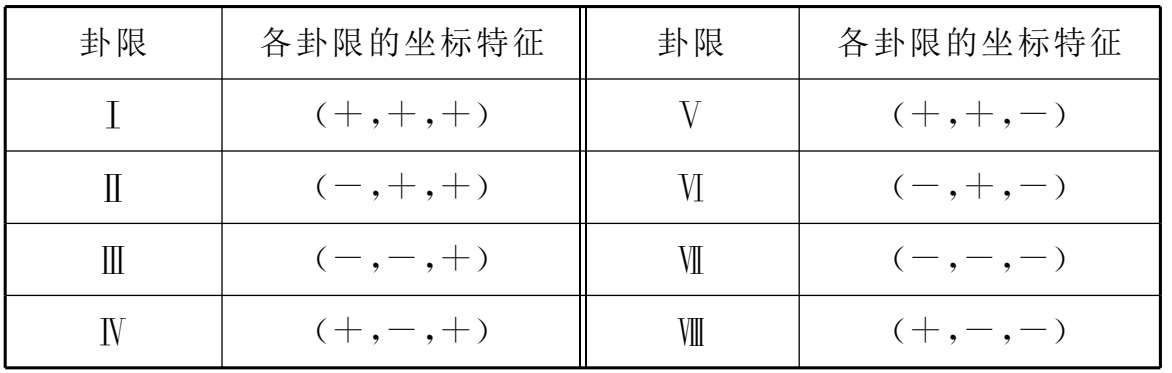
空间直角坐标系中坐标轴、坐标面上点的坐标特征列表如下(见表1-2):
表1-2
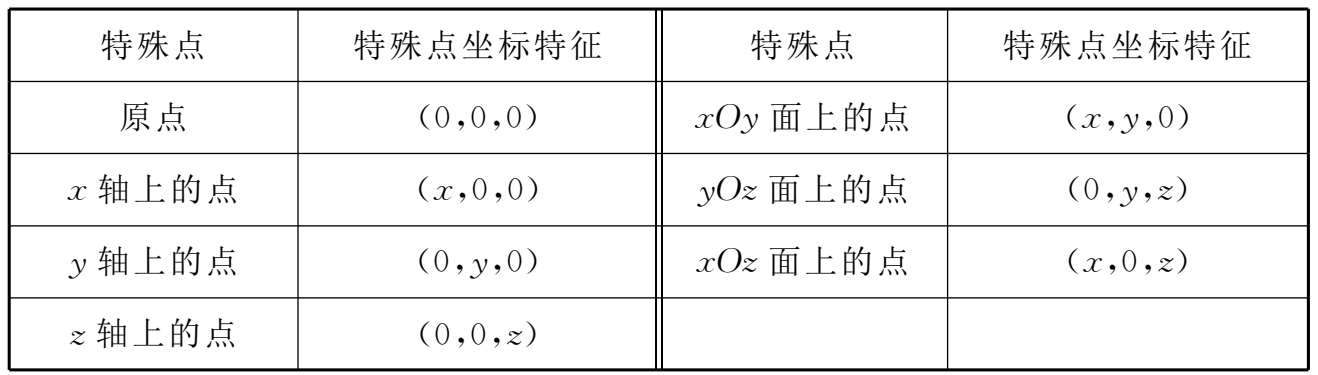
本节的引入问题就可通过建立空间直角坐标系来解决.若以教学楼大门为原点,向西方向为 x 轴正向,向上方向为 z 轴正向,根据右手法则,向南方向为 y 轴正向,则学生所在位置可表示为(5,-10,4)(单位:m)。
如图1-4所示,设 M 1 ( x 1 , y 1 , z 1 )、 M 2 (x 2 ,y 2 ,z 2 )为空间两点,过点M 1 、M 2 分别作垂直于三条坐标轴的六个平面,它们围成一个以 M 1 M 2 为对角线的长方体,其长、宽、高三条棱的长度分别为:
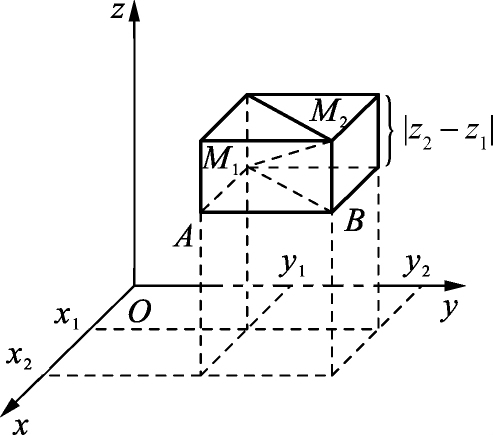
图1-4
| x 2 - x 1 |,| y 2 - y 1 |,| z 2 - z 1 |。
根据几何知识,长方体的对角线的平方等于三条棱长的平方和,即
| M 1 M 2 | 2 =| x 2 - x 1 | 2 +| y 2 - y 1 | 2 +| z 2 - z 1 | 2 ,
于是
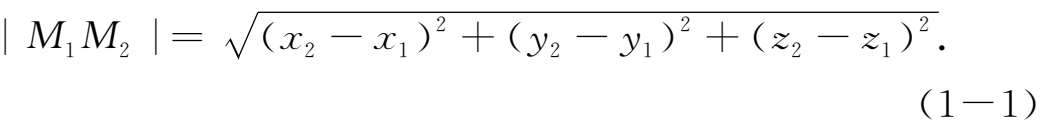
公式(1-1)称为 空间两点间的距离公式。 它是平面上两点间距离公式的推广。
特别地,点 M ( x , y , z )与原点 O 的距离公式为

例1 求点 M ( x , y , z )到三条坐标轴的距离。
解 设点 M 在 x 轴上的投影为点 P (如图1-3),则点 P 的坐标为 P ( x ,0,0),根据三垂线定理可知 MP ⊥ x 轴,即线段 MP 的长度就是 M 到 x 轴的距离,由公式(1-1),得
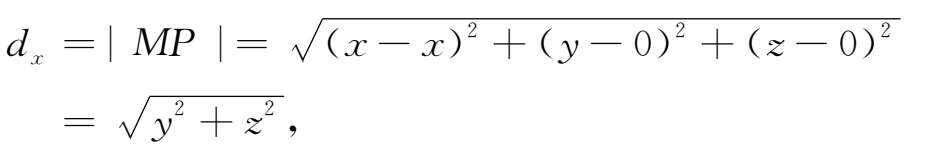
同理可得,点 M 到 y 轴、 z 轴的距离分别为
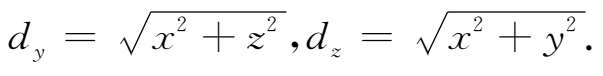
例2 已知点 A (7,-1,12), B (1,7,-12),在 z 轴上求一点 C ,使得∠ ACB 为直角。
解 由题意设点 C 的坐标为(0,0, z ),由公式(1-1),得
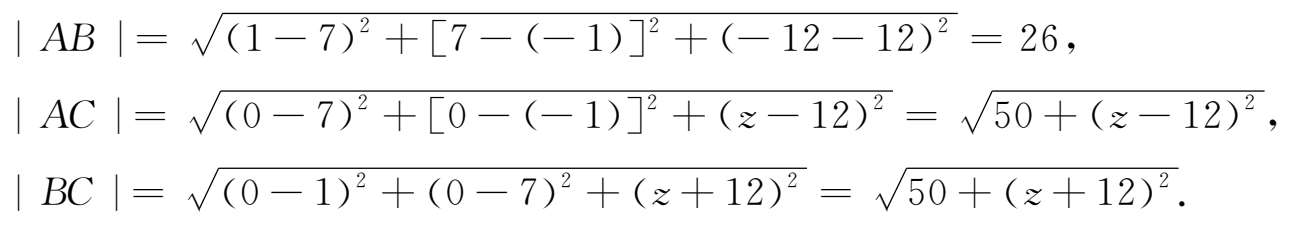
要使得∠ ACB 为直角,必有| AC | 2 +| BC | 2 =| AB | 2 ,即
[50+( z -12) 2 ]+[50+( z +12) 2 ]=26 2 ,
解得
z =±12。
所求点 C 为(0,0,12)或(0,0,-12)。
例3
设点
P
在
x
轴上,它到点
P
1
(0,
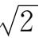 ,3)的距离为到点
P
2
(0,1,-1)的距离的两倍,求点
P
的坐标。
,3)的距离为到点
P
2
(0,1,-1)的距离的两倍,求点
P
的坐标。
解 设点 P 的坐标为( x ,0,0),依题意有
| PP 1 |=2| PP 2 |,
即
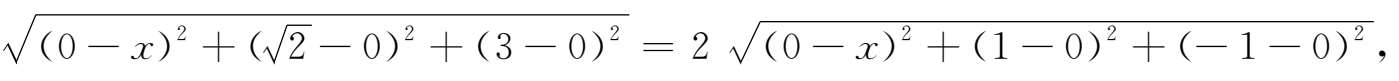
将上式两边平方,解得
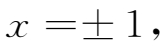
故所求的点 P 为(-1,0,0)或(1,0,0)。
在力学、物理学中,常常遇到两种类型的量,一种是如时间、温度、长度、质量、功等,只有大小,用一个实数就完全可以表示的量,这种量叫作 数量(标量); 另一种是如力、速度、位移、电场强度等既有大小又有方向的量,这种既有大小又有方向的量叫作 向量(矢量)。
向量通常用黑体小写字母
a
,
b
,
c
等表示,手写时可用标上箭头的小写字母表示,如
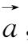
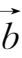 ,
,
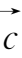 等.几何上,常用有向线段表示向量,起点为
A
、终点为
B
的向量记作
等.几何上,常用有向线段表示向量,起点为
A
、终点为
B
的向量记作
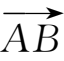
需要说明的是,为避免读者书写错误,本章用标上箭头的字母表示向量。
向量的长度称为向量的
模
,用
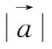 或
或
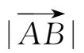 等表示。
等表示。
模等于0的向量,称为零向量,记作
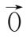 .零向量的方向可以看作任意的。
.零向量的方向可以看作任意的。
模等于1的向量称为
单位向量
.与非零向量
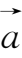 同向的单位向量记作
同向的单位向量记作
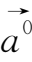 ,且有
,且有
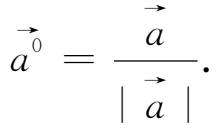
如果两个向量
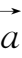 和
和
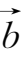 的模相等且方向相同,则称向量
的模相等且方向相同,则称向量
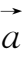 和
和
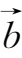 是
相等的向量,
记作
是
相等的向量,
记作
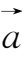 =
=
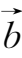 .根据这个规定,一个向量经过平行移动后能完全重合的向量是相等的向量.如果两个向量的模相等而方向相反,这时称其中一个向量是另一个向量的
负向量
,例如,向量
.根据这个规定,一个向量经过平行移动后能完全重合的向量是相等的向量.如果两个向量的模相等而方向相反,这时称其中一个向量是另一个向量的
负向量
,例如,向量
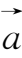 的负向量记为-
的负向量记为-
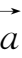 ,由负向量的定义可知-(-
,由负向量的定义可知-(-
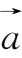 )=
)=
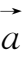 。
。
注意
向量只有相等与不相等之分,没有大小关系之别,即“大于”或“小于”的概念对向量不适用。如
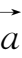 >
>
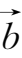 ,
,
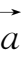 =3没有意义,但
=3没有意义,但
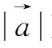 >
>
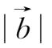 ,
,
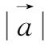 =3有意义。
=3有意义。
(1)向量的加法.两个向量
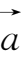 ,
,
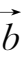 的和仍是向量,记作
的和仍是向量,记作
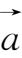 +
+
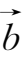 =
=
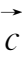 。
。
仿照物理学中力的合成可得向量和的
平行四边形法则
,如图1-5所示.由于向量可以平移,所以若把
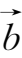 的起点平移到
的起点平移到
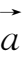 的终点上,则以
的终点上,则以
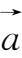 的起点为起点,以
的起点为起点,以
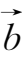 的终点为终点的向量即为
的终点为终点的向量即为
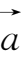 +
+
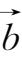 ,这种表示向量和的方法称为向量加法的
三角形法则
,如图1-6所示。
,这种表示向量和的方法称为向量加法的
三角形法则
,如图1-6所示。
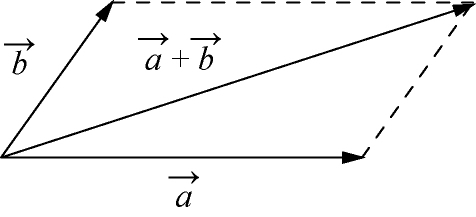
图1-5
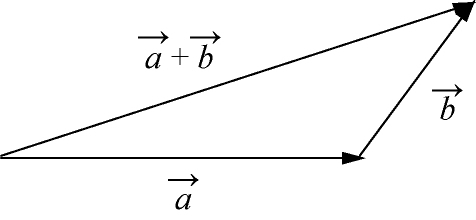
图1-6
向量的加法满足如下运算规律:
① 交换律:
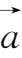 +
+
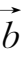 =
=
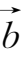 +
+
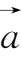 ;
;
② 结合律:(
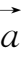 +
+
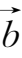 )+
)+
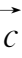 =
=
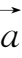 +(
+(
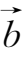 +
+
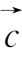 )。
)。
(2)向量的减法.向量的减法是加法的逆运算.若
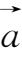 -
-
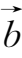 =
=
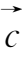 ,即
,即
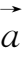 +(-
+(-
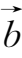 )=
)=
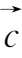 ,根据向量加法的三角形法则,可得向量减法的作图方法(如图1-7)。
,根据向量加法的三角形法则,可得向量减法的作图方法(如图1-7)。
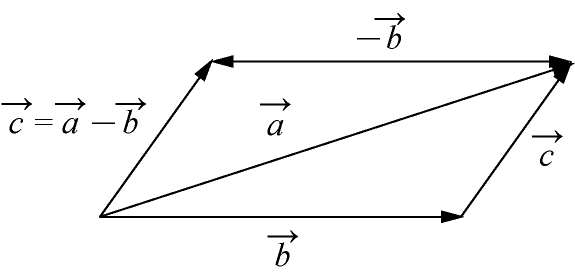
图1-7
(3)向量的数乘.设
λ
是一个数,向量
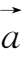 与数
λ
的乘积记为一个向量,记作
λ
与数
λ
的乘积记为一个向量,记作
λ
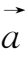 ,规定:
,规定:
①当
λ
>0时,
λ
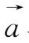 与
与
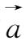 同向,
同向,
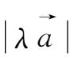 =
λ
=
λ
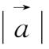 ;
;
②当
λ
=0时,
λ
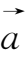 =
=
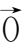 ;
;
③当
λ
<0时,
λ
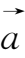 与
与
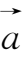 反向,
反向,
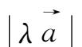 =
=
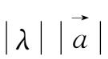 。
。
向量的数乘满足如下运算规律:
设
λ
,
μ
是两个实数,
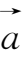 是一个向量,则有
是一个向量,则有
①结合律:
λ
(
μ
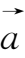 )=
μ
(
λ
)=
μ
(
λ
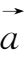 )=(
λμ
)=(
λμ
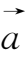 );
);
②分配律:(
λ
+
μ
)
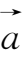 =
λ
=
λ
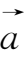 +
μ
+
μ
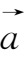 。
。
向量的加(减)法运算及数乘运算统称为向量的 线性运算。
(1)向量
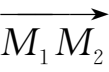 的坐标表示.在空间直角坐标系中,沿
x
轴、
y
轴、
z
轴正向分别取单位向量,称为
基本单位向量
,分别记作
的坐标表示.在空间直角坐标系中,沿
x
轴、
y
轴、
z
轴正向分别取单位向量,称为
基本单位向量
,分别记作
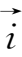 ,
,
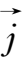 ,
,
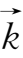 。
。
设向量
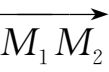 的起点为
M
1
(
x
1
,
y
1
,
z
1
),终点为
M
2
(
x
2
,
y
2
,
z
2
)(如图1-8).根据向量的数乘运算及向量相等的定义,得
的起点为
M
1
(
x
1
,
y
1
,
z
1
),终点为
M
2
(
x
2
,
y
2
,
z
2
)(如图1-8).根据向量的数乘运算及向量相等的定义,得
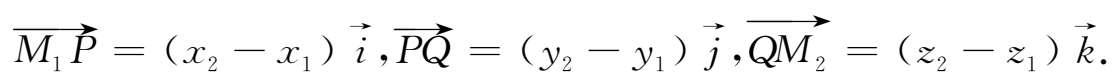
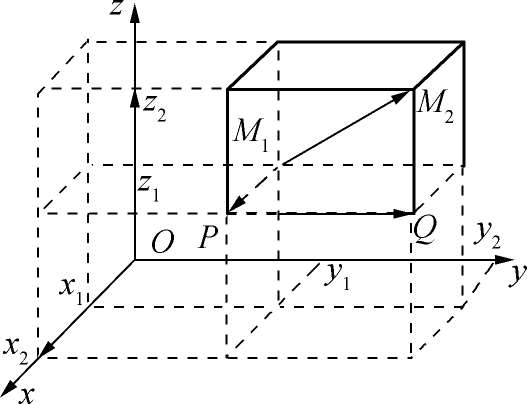
图1-8
由向量的加法,得
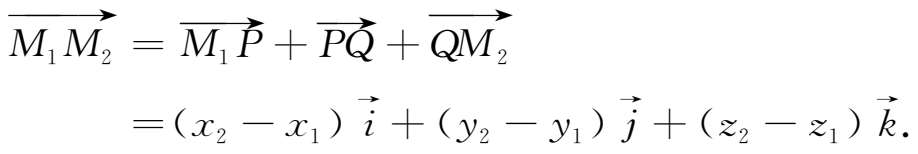
因此,向量
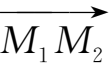 可以由其在
x
,
y
,
z
轴的分向量(
x
2
-
x
1
)
可以由其在
x
,
y
,
z
轴的分向量(
x
2
-
x
1
)
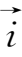 ,(
y
2
-
y
1
)
,(
y
2
-
y
1
)
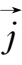 ,(
z
2
-
z
1
)
,(
z
2
-
z
1
)
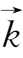 表示.由于向量
表示.由于向量
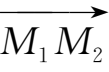 与有序数组
x
2
-
x
1
,
y
2
-
y
1
,
z
2
-
z
1
存在一一对应关系,故可用它来表示向量
与有序数组
x
2
-
x
1
,
y
2
-
y
1
,
z
2
-
z
1
存在一一对应关系,故可用它来表示向量
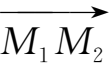 ,记作
,记作
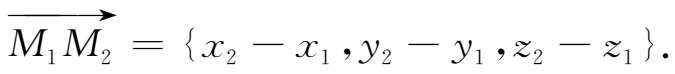
上式称为
向量
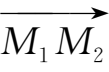 的坐标表示式。
向量
的坐标表示式。
向量
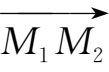 在三条坐标轴上的投影
x
2
-
x
1
,
y
2
-
y
1
,
z
2
-
z
1
称为
向量
在三条坐标轴上的投影
x
2
-
x
1
,
y
2
-
y
1
,
z
2
-
z
1
称为
向量
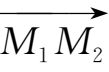 的坐标。
的坐标。
特别地,以原点
O
为起点、
M
(
a
x
,
a
y
,
a
z
)为终点的
向量
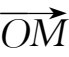 (如图1-9)的坐标表示式为
(如图1-9)的坐标表示式为
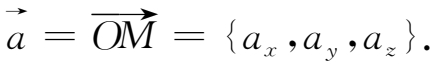
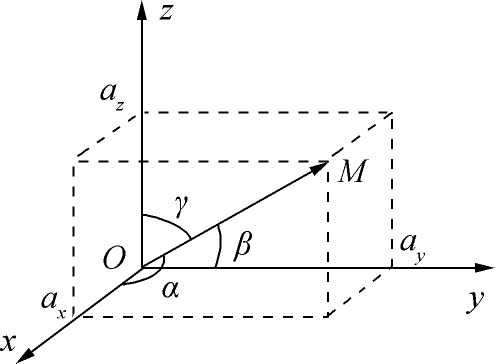
图1-9
注意
向量的坐标表示式不能与点的坐标混淆。例如
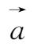 ={1,-2,0}表示向量,A(1,-2,0)则表示点A.
={1,-2,0}表示向量,A(1,-2,0)则表示点A.
例4 一向量的坐标为{4,-4,7},它的终点在点 P (2,-1,7),求这个向量的起点 M 的坐标。
解 设向量的起点 M 的坐标为( x , y , z ),则有
4=2- x ,-4=-1- y ,7=7- z ,
即得 x =-2, y =3, z =0,故起点 M 的坐标为(-2,3,0)。
(2)向量的模及方向余弦的坐标表示.任一非零向量
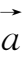 ={
a
x
,
a
y
,
a
z
}都可将其看作以原点
O
为起点,
M
(
a
x
,
a
y
,
a
z
)为终点的向量
={
a
x
,
a
y
,
a
z
}都可将其看作以原点
O
为起点,
M
(
a
x
,
a
y
,
a
z
)为终点的向量
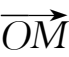 ,即
,即
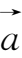 =
=
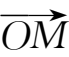 .由空间两点间的距离公式,可知向量
.由空间两点间的距离公式,可知向量
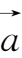 ={
a
x
,
a
y
,
a
z
}的模
={
a
x
,
a
y
,
a
z
}的模
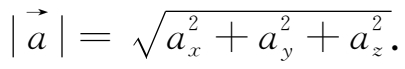
非零向量
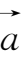 ={
a
x
,
a
y
,
a
z
}的方向可以分别用向量
={
a
x
,
a
y
,
a
z
}的方向可以分别用向量
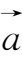 与
x
轴、
y
轴、
z
轴正向的夹角来确定(如图1-9)。
与
x
轴、
y
轴、
z
轴正向的夹角来确定(如图1-9)。
定义1-1
非零向量
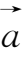 与
x
轴、
y
轴、
z
轴正向的夹角称为
方向角
,分别记作
α
,
β
,
γ
(其中0≤
α
≤π,0≤
β
≤π,0≤
γ
≤π),方向角的余弦称为非零向量
与
x
轴、
y
轴、
z
轴正向的夹角称为
方向角
,分别记作
α
,
β
,
γ
(其中0≤
α
≤π,0≤
β
≤π,0≤
γ
≤π),方向角的余弦称为非零向量
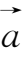 的
方向余弦。
的
方向余弦。
由图1-9可知,非零向量
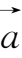 ={
a
x
,
a
y
,
a
z
}的方向余弦的坐标表示式为
={
a
x
,
a
y
,
a
z
}的方向余弦的坐标表示式为
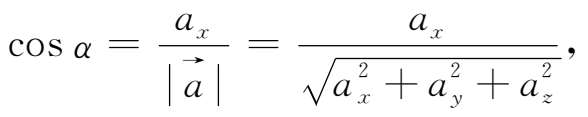
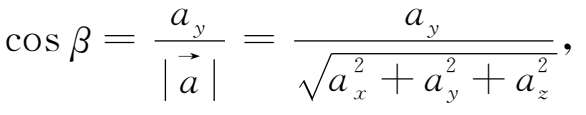
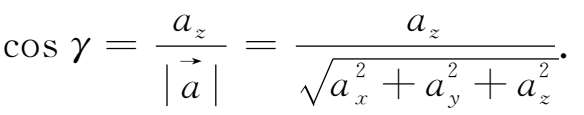
显然,方向余弦满足以下关系式
cos 2 α +cos 2 β +cos 2 γ =1。
与非零向量
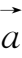 同方向的单位向量的坐标表示为
同方向的单位向量的坐标表示为
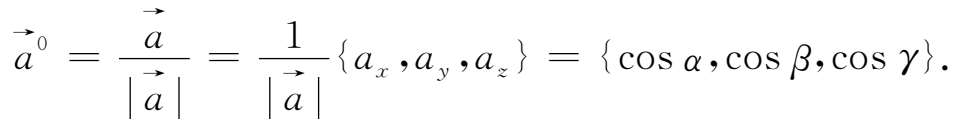
(3)向量线性运算的坐标表示.利用向量的坐标表示,可以将向量的线性运算转化为坐标间的代数运算。
设向量
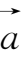 ={
a
x
,
a
y
,
a
z
},
={
a
x
,
a
y
,
a
z
},
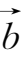 ={
b
x
,
b
y
,
b
z
},则有
={
b
x
,
b
y
,
b
z
},则有
①
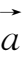 +
+
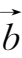 ={
a
x
+
b
x
,
a
y
+
b
y
,
a
z
+
b
z
};
={
a
x
+
b
x
,
a
y
+
b
y
,
a
z
+
b
z
};
②
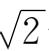 -
-
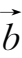 ={
a
x
-
b
x
,
a
y
-
b
y
,
a
z
-
b
z
};
={
a
x
-
b
x
,
a
y
-
b
y
,
a
z
-
b
z
};
③
λ
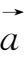 ={
λ
a
x
,
λ
a
y
,
λ
a
z
}(
λ
为实数);
={
λ
a
x
,
λ
a
y
,
λ
a
z
}(
λ
为实数);
④
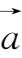 ∥
∥
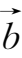
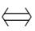
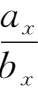 =
=
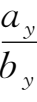 =
=
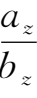 (若
b
x
,
b
y
,
b
z
中某一个为零,相应的分子也为零)。
(若
b
x
,
b
y
,
b
z
中某一个为零,相应的分子也为零)。
例5
求点A(4,0,1),B(3,
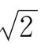 ,2)所确定的向量
,2)所确定的向量
 的坐标、模、方向余弦和方向角及与
的坐标、模、方向余弦和方向角及与
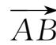 同方向的单位向量
同方向的单位向量
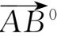
解
向量的坐标
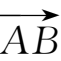 ={
x
,
y
,
z
}={3-4,
={
x
,
y
,
z
}={3-4,
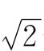 -0,2-1}={-1,
-0,2-1}={-1,
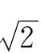 ,
1}。
,
1}。
向量
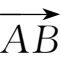 的模
的模
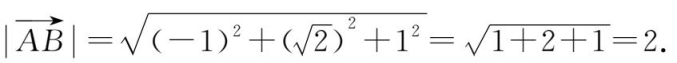
向量
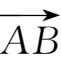 的方向余弦cos
α
=
的方向余弦cos
α
=
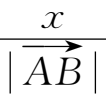 =-
=-
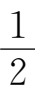 ,方向角为
α
=
,方向角为
α
=
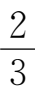 π,
π,
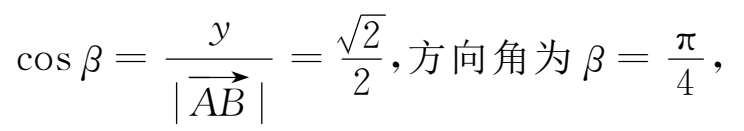
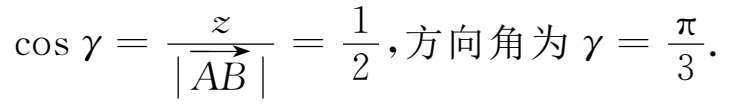
单位向量
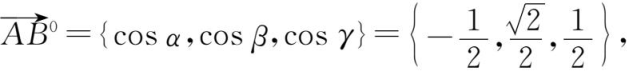
或
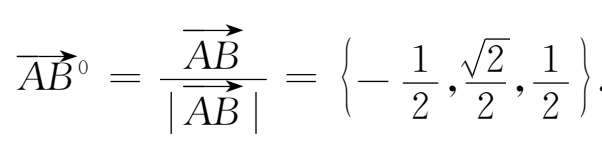
例6
设向量
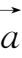 的方向角
α
=
的方向角
α
=
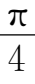 ,
β
=
,
β
=
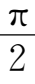 ,
γ
为锐角,且
,
γ
为锐角,且
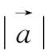 =2,求向量
=2,求向量
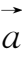 的坐标表示式。
的坐标表示式。
解 因为cos 2 α +cos 2 β +cos 2 γ =1,
且
α
=
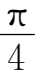 ,
β
=
,
β
=
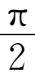 ,
γ
为锐角,
,
γ
为锐角,
于是有
cos
γ
=
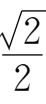 (cos
γ
=-
(cos
γ
=-
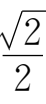 不合题意,舍去),
不合题意,舍去),
所以
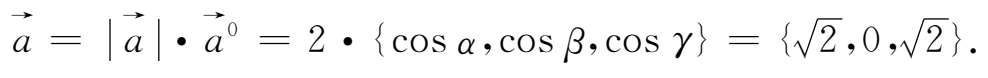
1.写出点 M (-1,2,3)关于原点、三个坐标轴、三个坐标平面的对称点的坐标。
2.在 P (1,-5,2), Q (1,2,-1), R (1,0,3)中,哪一个点在 xOz 平面之中?哪一个点距离 xOy 平面最近?
3.设
α
,
β
,
γ
是向量
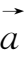 的三个方向角,则sin
2
α
+sin
2
β
+sin
2
γ
为多少?
的三个方向角,则sin
2
α
+sin
2
β
+sin
2
γ
为多少?
1.在 x 轴上求与两点 P 1 (-4,1,7)和 P 2 (3,5-2)等距离的点。
2.求证以 M 1 (4,3,1), M 2 (7,1,2), M 3 (5,2,3)三点为顶点的三角形是一个等腰三角形。
3.求点 P (3,-1,2)到原点及三个坐标轴的距离。
4.在 yOz 平面上,求与 A (3,1,2), B (4,-2,-2), C (0,5,1)等距离的点。
5.已知
A
(-2,3,5),
B
(1,-1,
z
),
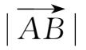 =13,求点
B
的未知坐标。
=13,求点
B
的未知坐标。
6.求向量
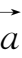 ={2,-5,
={2,-5,
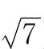 }的模、方向余弦及与
}的模、方向余弦及与
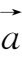 同方向的单位向量。
同方向的单位向量。
7.【
平衡合力
】已知力
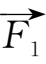 ={1,1,3},
={1,1,3},
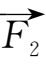 ={2,-3,1}作用于同一点,问如何使力才能与
={2,-3,1}作用于同一点,问如何使力才能与
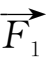 和
和
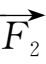 的合力达到平衡?
的合力达到平衡?
8.已知
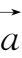 ={3,2,5},
={3,2,5},
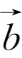 ={2,4,3},
={2,4,3},
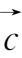 =
=
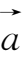 -
-
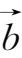 ,求向量
,求向量
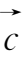 的方向余弦及与
的方向余弦及与
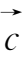 平行的单位向量。
平行的单位向量。
9.已知两点
M
1
(1,-
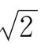 ,5),
M
2
(2,0,4),求向量
,5),
M
2
(2,0,4),求向量
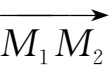 的模、方向余弦、方向角及与
的模、方向余弦、方向角及与
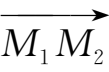 同方向的单位向量
同方向的单位向量
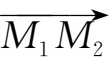 0
。
0
。
10.设向量
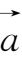 与各坐标轴成相等的锐角,
与各坐标轴成相等的锐角,
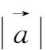 =
=
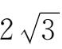 ,求向量
,求向量
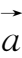 的坐标表示式。
的坐标表示式。
11.设向量
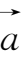 的方向角
α
=
的方向角
α
=
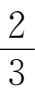 π,
β
=
π,
β
=
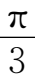 ,
γ
为锐角,且
,
γ
为锐角,且
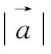 =4,求向量
=4,求向量
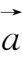 的坐标表示式。
的坐标表示式。