





建立语音信号的产生模型对于语音处理而言具有重要的意义。前面介绍了发声器官和语音的产生,有了这些基础便可以建立一个离散时域的语音信号的产生模型。当然,要建立一个十分精确的语音信号的产生模型是很困难的,这是因为语音的产生不仅是一个复杂的生理和心理过程,而且与声道的形状、声道中的声激励等因素都有关系。本节仅给出一个比较简单的模型(如图2-9所示),这个模型可以满足大多数语音处理研究和应用的需要。
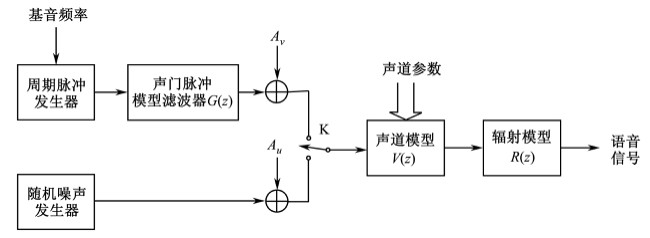
图2-9 语音信号的产生模型
图2-9中的语音信号的产生模型包括三个部分:激励源、声道模型和辐射模型。激励源分为浊音和清音两种。由浊音/清音开关K所处的位置来决定产生的语音是浊音还是清音。浊音时,激励信号由一个周期脉冲发生器产生,产生的序列是一个频率等于基音频率的冲激序列。为了使浊音的激励信号具有声门脉冲的实际波形,还需要使上述的冲激序列通过一个声门脉冲模型滤波器G(z)。对声门波形的频谱分析表明,其幅度频谱按每倍频程12dB的速度递减,如果令
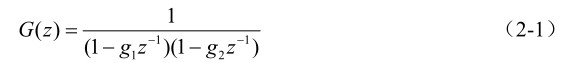
其中g 1 和g 2 都很接近于1,那么由之形成的浊音激励信号的频谱很接近于声门脉冲的频谱。图2-9中的乘系数A v 的作用是调节浊音信号的幅度。
清音时,激励信号由一个随机噪声发生器产生。可设定其平均值为0,其自相关函数是一个单位冲激函数。这表明它的任何两个不同样点都不相关且其均方差值为1。此外,还假定它的幅度具有正态概率分布。图2-9中的乘系数A u 的作用是调节清音信号的幅度。
声道模型V(z)给出了离散时域的声道传输函数。将实际声道作为一个变截面声管加以研究并采用流体力学的方法,就可以导出该模型。在大多数情况下,V(z)是一个全极点函数。因此,V(z)可以表示为

式中,a 0 =1,a i 为实数。这里,把截面积连续变化的声管近似为p段短声管的串联,每段短声管的截面积是不变的,p称为这个全极点滤波器的阶。显然,p值取得越大,模型的传输函数与声道实际传输函数的吻合程度就越高。一般地,对大多数实际应用而言,p值取8~12。若p取偶数,一般有p/2对共轭极点,极点的频率分别与语音的各个共振峰相对应。
辐射模型R(z)与嘴型有关,一般可以表示为
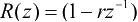 ,r≈1。
,r≈1。
在语音信号的产生模型中,除了G(z)和R(z)保持不变以外,基音频率、A v 、A u 、浊音/清音开关的位置及声道模型中的参数都是随时间变化而变化的。由于发声器官的惯性使得这些参数的变化速度受到限制。对于声道参数而言,在10~30ms的时间间隔内可以认为它们保持不变,因此语音的短时分析帧长一般取为10~30ms左右。对于激励源参数而言,大部分情况下这一结论也是正确的。但有些音的变化速度特别快,如塞音[t]或塞擦音[c]的爆破段,20ms时间间隔就过长,这时取5ms的间隔更为恰当。此外,语音信号的产生模型将语音信号截然分为周期脉冲激励和噪声激励两种情况,与实际情况也不完全符合。如果将此模型的激励源改为上述两种激励按任意比例相叠加,就更加接近于实际情况。除了上面讨论的一些限制以外,语音信号的产生模型的局限性主要表现在它的传输函数不包含有限传输零点,而像鼻音、擦音这样一些音的声道传输函数中是包含有限零点的。一种解决问题的方案是在V(z)中引入若干有限传输零点,但是这将使模型复杂化;另一种方法是适当提高阶数p,使得全极点模型能更好地逼近具有此种零点的传输函数。
根据语音信号的产生模型,离散时域语音信号s(n)的Z变换S(z)可以用一个统一的公式来计算:

在浊音的情况下,E(z)是一个周期冲激序列的Z变换,且A=A v ,H(z)=G(z)V(z)R(z);在清音的情况下,E(z)则是一个随机噪声的Z变换,且A=A u ,H(z)=V(z)R(z)。