




定义:若集合A和集合B之间存在一一映射,则称集合A和集合B对等,记作A~B。
【例 1-1】集合{1,2}对等于集合{0,2}。
【例 1-2】集合A={1,2,3,4,5,…}对等于集合B={2,4,6,8,10,…},在本例中,集合A和自己的一个真子集B存在着对等关系,这种与自身真子集存在对等关系的情况不可能发生在元素个数有限的集合(有限集)中,只有无限集合才可能具有这一性质。
【例 1-3】图 1-3 中线段AB和CD是点构成的集合,对于AB上的任意一点P,都可以用图示的方法对应到CD上的一点P′,反之亦然,所以集合AB和CD是对等的。
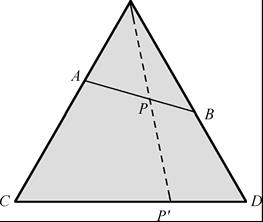
图 1-3 集合AB和CD对等
元素的个数是对集合大小的很自然的描述。对于有限集,元素的个数是可以数得过来的,或者说等于某个自然数。但对于无限集,由于其中元素个数为无穷多个,怎么比较大小呢?康托尔从对等的概念出发,认为互相对等的集合元素个数是相同的,把对等集合的这个公共的性质归纳出来,就称为集合的基数。我们把相互对等的集合归为一类,称其公共的“元素个数”为这一类集合的基数或势。规定空集的基数为零、有限集的基数为自然数、无限集的基数为超限数。
集合论的魅力表现在无限集合中,我们遇到的第一个无限集合是自然数集合N={0,1,2,3,4…},称自然数集N的基数为ℵ 0 ,读作阿列夫零。
定义:凡是能与自然数集N对等的集合统称为可列集,不是可列集的无限集合称为不可列集。因此,所有可列集的基数都是ℵ 0 。
【例 1-4】如下 4 个集合都是可列集:
(1){1,2,3,4…};
(2){2,4,6,8…};
(3){1,1/2, 1/3,1/4…};
(4){…-3,-2,-1,0,1,2,3…}。
下面我们不加证明地给出可列集的一些性质:
(1)有限个可列集的并集是可列集;
(2)可列个可列集的并集是可列集;
(3)若集合A, B是可列集,则A×B是可列集。
定理 1-1:有理数集Q是可列集。
定理 1-2:实数集R是不可列集。
把实数集R的超限基数记作c,根据集合论中连续统假设,有 2ℵ 0 = c,且不存在集合,其基数介于ℵ 0 和c之间。实数集似乎已经很大了,那么还有没有无限集合其基数大于c呢?答案是肯定的。如果一个有限集A的基数是a,则不难验证A的幂集 2 A 的基数是 2 a > a。类似的结论对于无限集也成立,实数集的幂集的基数是 2 c > c,如果把这个取幂集的操作持续做下去,则其基数将持续增长,所以基数没有最大的。
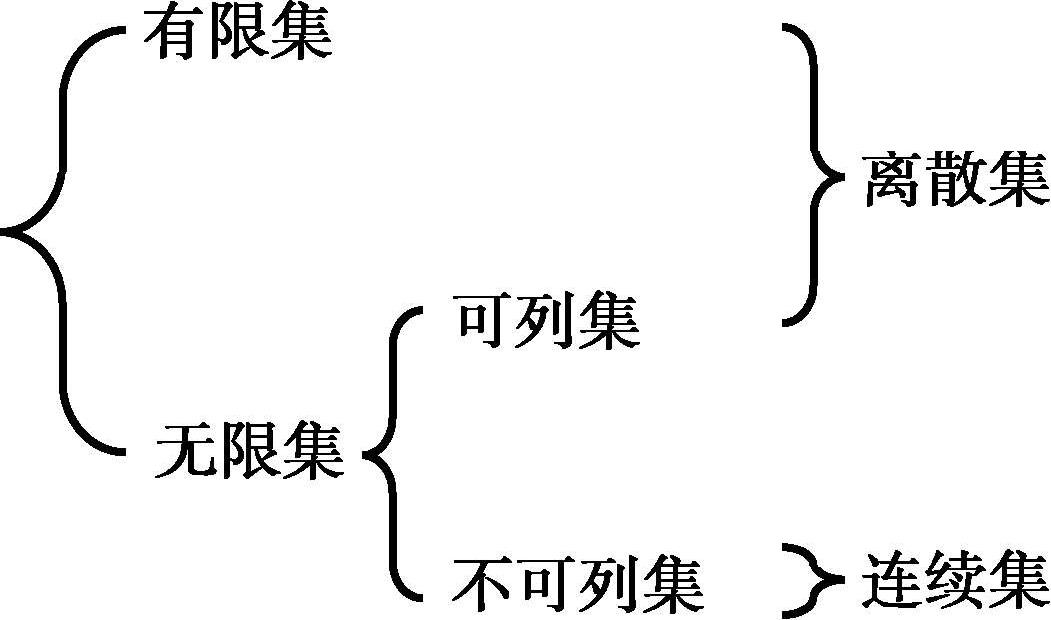
图 1-4 集合的分类关系
根据 1.4.2 节的讨论,我们可以根据集合的基数对集合加以分类,分为有限集和无限集,无限集又分为可列集和不可列集。在工程应用中,经常用术语离散集和连续集,其中离散集包括了有限集和可列集,连续集则指不可列集。其分类关系如图 1-4 所示。
按照基数从小到大的次序可以把各种集合排序,如表 1-1 所示。
表 1-1 集合基数的比较
