
下载掌阅APP,畅读海量书库
立即打开




设X和Y是两个非空集合,若存在一个规则f,使得对于X中的每一个元素x,按照f,都存在Y中的唯一一个元素y与之相对应,则称f是定义在X上取值在Y中的映射,记作f: X→ Y。X是f的定义域,集合ran(f)={y|y=f(x), x∈ X}是f的值域;x和y分别称为映射f的原象和象。
对于映射f的值域ran(f )中的每个象元素y,若唯一的存在自己的原象x,则称该映射为单射。
如果集合Y中每个元素y都存在原象x,即Y就是映射f的值域Y=ran(f),则称该映射为满射。
既是单射又是满射的映射称为一一映射。
4 种映射的示意如图 1-2 所示。
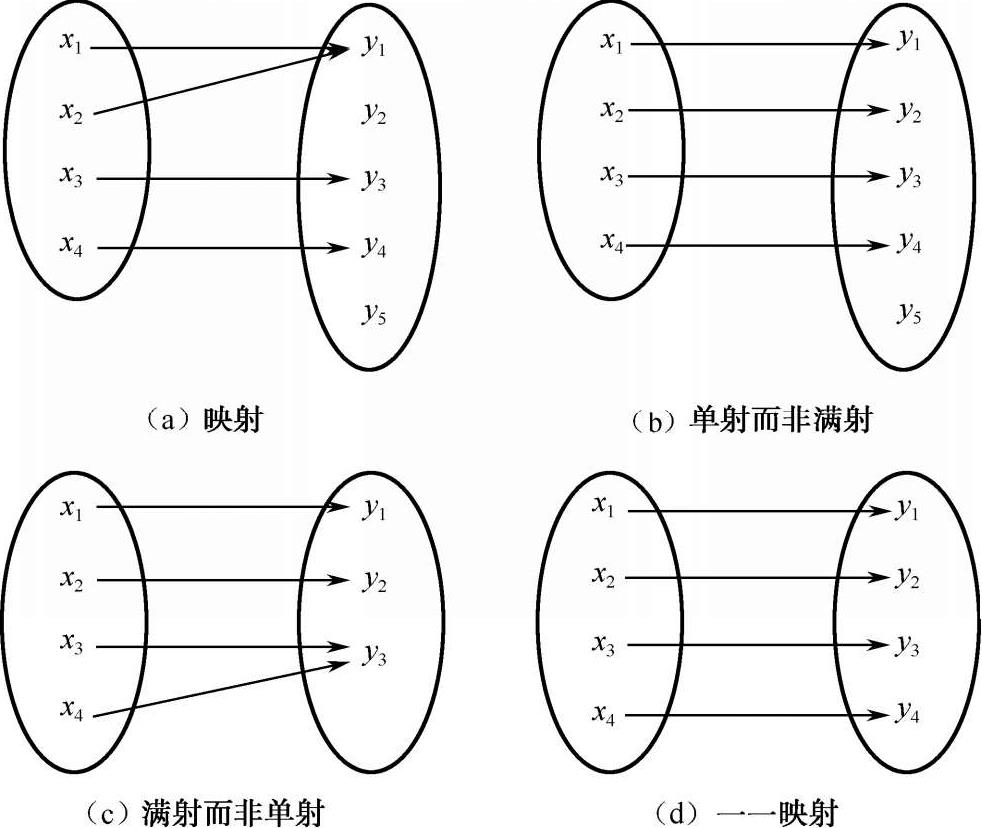
图 1-2 映射