




集合的运算是指集合与集合之间的运算,包括交、并、差、补、笛卡儿积和幂集,这些运算的结果是一个新的集合。可以用文氏图(Voronoi diagram)清楚直观地表示集合的运算。在文氏图中,以大的矩形区域表示全集Ω,以矩形区域内部小的区域表示各个子集。
交运算用描述法表示为:A∩B={x| x∈ A且x∈ B}。A∩B也可记作AB。当两个集合没有交集,即A∩B=∅时,称A和B互不相容或互斥。
并运算用描述法表示为:A∪B={x| x∈ A或x∈ B}。当且仅当A和B互不相容时,A∪B也可以记作A+B。特别地,当A∩B=∅且A∪B=Ω时,称A和B是对立的。推广到有限多个集合的情形,对于集合A 1 ,A 2 ,A 3 ,…,A n ,若
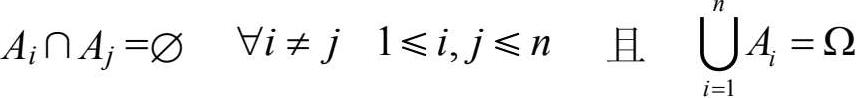
则称A 1 ,A 2 ,A 3 ,…,A n 为完备互斥的。
差运算用描述法表示为:A\B={x| x∈ A且x∉ B},不难证明,A\B= AB c 。
集合A的补集定义为全集Ω和集合A的差集,即A
c
=Ω\A,集合A的补集由全集Ω中所有不属于集合A的元素构成,补集又称余集或绝对补集,也可记作
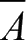 。
。
笛卡儿积又称为集合的乘积,其结果是一个新的集合,该集合由A和B中的元素组成的有序数对构成。因为是有序数对,所以笛卡儿积的运算不满足交换律,即A×B≠B×A。
集合A的幂集是一个集合类,由A的全部子集所构成,用 2 A 表示。
集合的各种运算结果用文氏图表示如图 1-1 中的阴影部分所示。
集合运算具有如下一些性质:
(1)交换律:
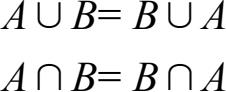
(2)结合律:
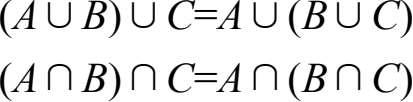
(3)分配律:(4)De Morgen律:
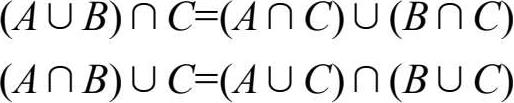
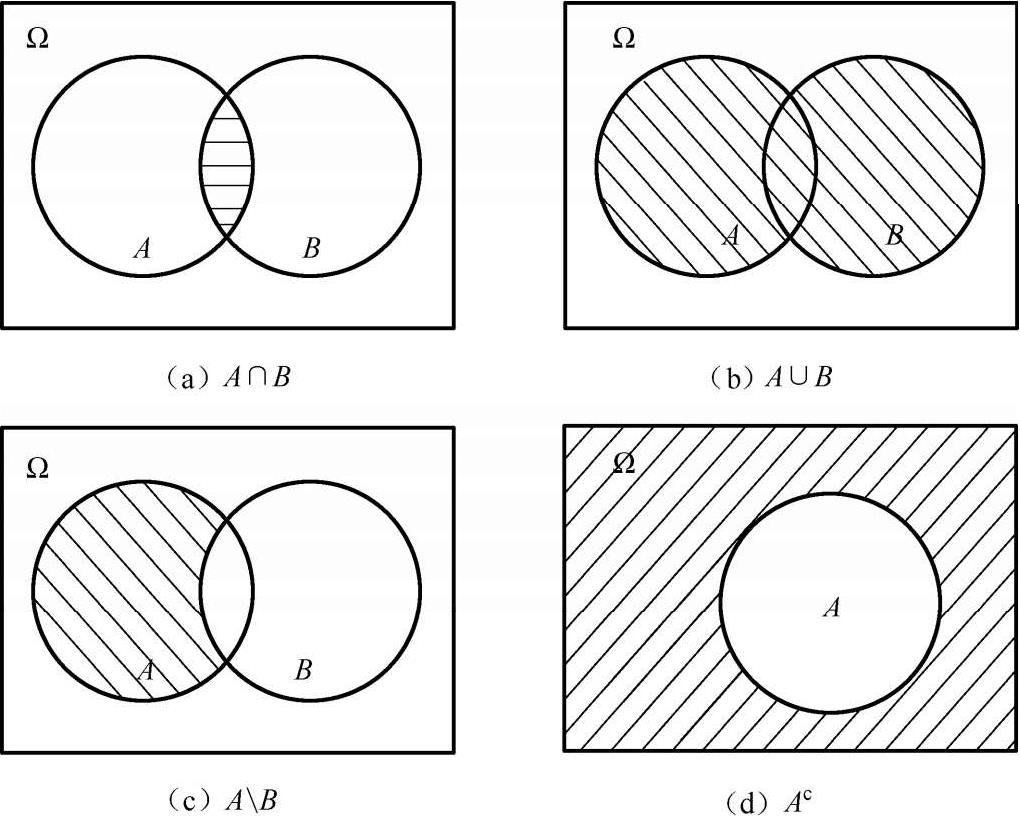
图 1-1 集合运算的文氏图表示
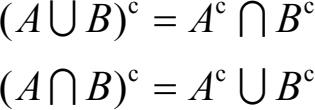
这些性质可以应用文氏图自行检验。