几何型随机试验基于点的集合,在该试验中,我们定义点落在某个集合中的概率为该集合的测度与全集的测度之比,即P(A)=L(A)/L(Ω)。几何概率,又称积分几何,把集合的类型加以推广,面对的是各种几何体(线、面、体),研究的是如何把概率的思想和方法应用到几何体构成的集合上,本书只以直线集合为例介绍几何概率的基本思想。
几何概率最早可以追溯到两个世纪以前的Buffon针问题。在该学科漫长而曲折的发展历史中,曾遭遇了如Bertrand悖论
[196][74]
等困境,一度动摇了其数学基础。为了摆脱这种尴尬境地,Poincaré建议限制几何概率的定义,使其满足几何群不变性准则。概率、测度、群、几何等概念构成了几何概率的数学基础。为了把概率的思想应用到随机几何对象上,首先需要定义这些几何对象的密度和测度。在几何概率中,平面上的一条直线由其到原点的距离s和其法线与x轴夹角θ所决定(如图 2-19 所示),(s,θ )同时也是从原点到该直线所做垂线的垂足的极坐标。进一步,定义ds dθ为平面上直线集合的密度,定义
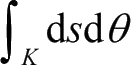 为区域K中直线集合的测度。简化起见,这里仅考虑K为凸集。根据几何概率的原理,这样定义的直线的密度和测度是唯一满足刚体运动群不变性的密度和测度。直线方程定义为
为区域K中直线集合的测度。简化起见,这里仅考虑K为凸集。根据几何概率的原理,这样定义的直线的密度和测度是唯一满足刚体运动群不变性的密度和测度。直线方程定义为
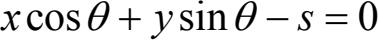
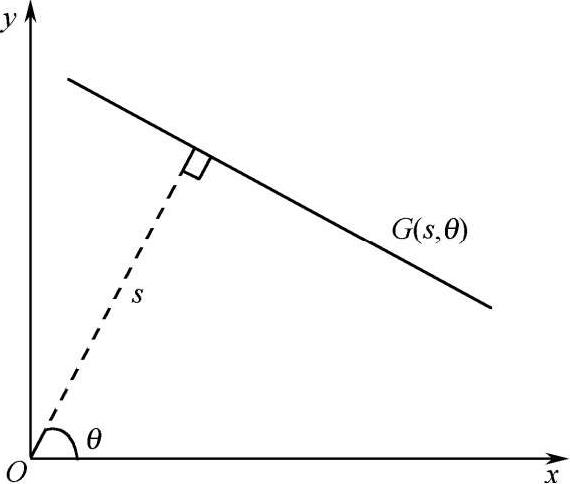
图 2-19 平面上的直线由其坐标(s ,θ)所决定
为了理解几何概率的思想,让我们讨论一下著名的Buffon针问题,如图 2-20所示。平面上以等间距d平行放置着无数根直线,把一根长度为l(l≤d)的针随机地抛掷在平面上,求针与直线相交的概率p。
解:以s表示针的中点距离最近直线的距离,以θ表示针与直线垂线的夹角。充分考虑针抛掷位置的对称性,则针的所有位置构成的集合的测度为
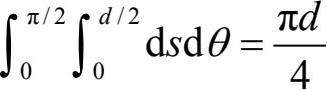
其中,考虑到只有当s小于等于(l/2)cosθ时,针才能与直线相交,所以,能够与直线相交的那些针的位置集合的测度为
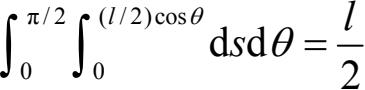
由此,针与直线相交的概率为
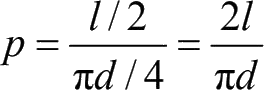
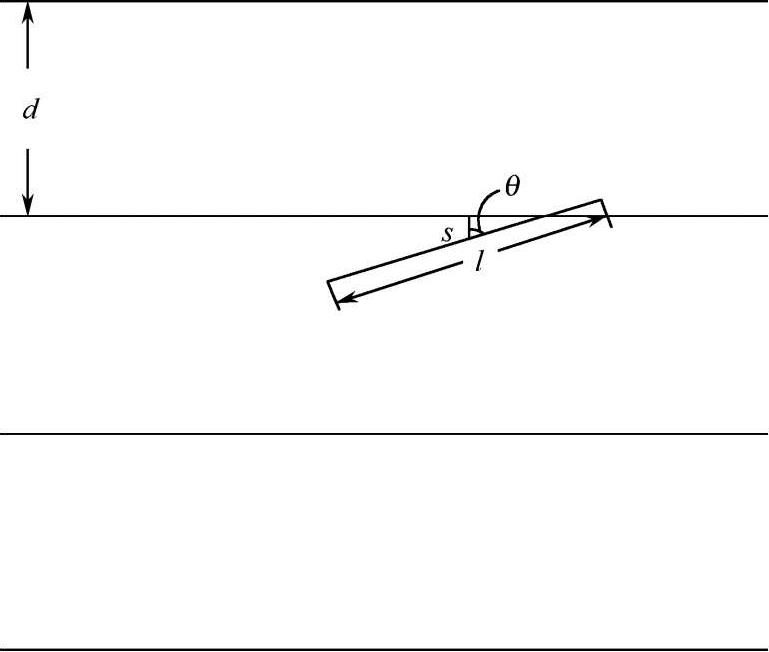
图 2-20 Buffon针问题
最后不加证明地给出与移动模型分析有关的几何概率的几个重要结论 [102] :
(1)与闭凸集K相交的直线集合的测度满足
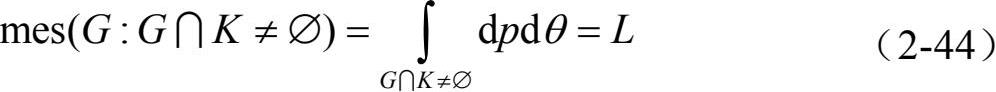
其中,mes(·)表示集合的测度,L是区域K的边界的周长,也就是说与有界闭凸集相交的直线集合的测度等于该凸集边界的周长。
(2)以σ表示直线G被凸集K所截得的弦长,则有
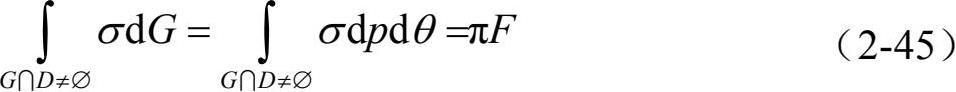
进一步,凸集K的平均弦长E(σ )满足

其中,F表示K的面积,L表示K的周长。
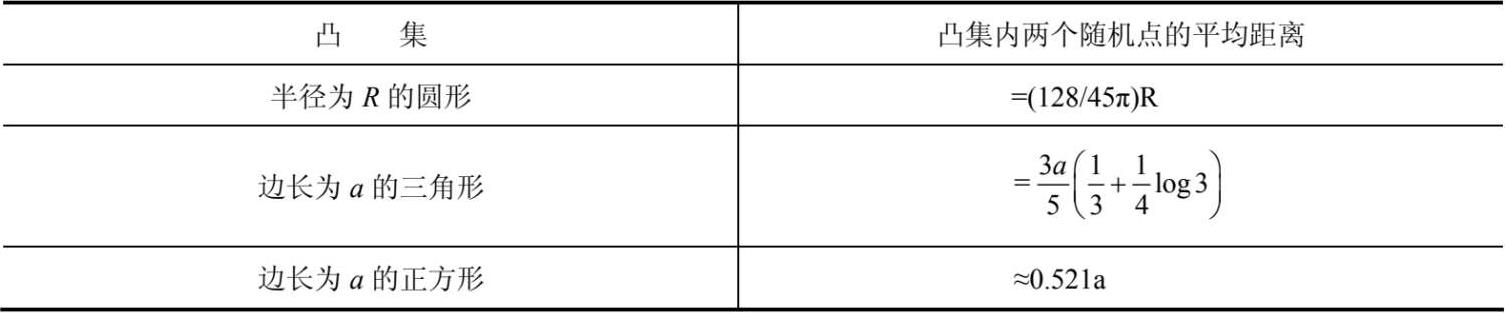
(3)凸集K中两个随机点的平均距离E(r)如表 2-6 所示。
表 2-6 凸集K中两个随机点的平均距离