




人们在长期的生产实践中发现,尽管单次随机试验具有不确定性,但大量的重复试验中,某事件A发生的频率具有稳定性,总是围绕在某个值(即该事件的概率)附近波动,而且试验次数越多,波动幅度越小,也就是越接近其概率值。大数定律就是这种现象的理论根据,反映了大量随机试验中某量的算术平均值将收敛于其统计平均值。
设
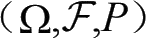 是某一概率空间,X=X(ω)是一个非负随机变量,则对于∀ ε> 0,有
是某一概率空间,X=X(ω)是一个非负随机变量,则对于∀ ε> 0,有

称该不等式为切比雪夫不等式。基本的切比雪夫不等式只是针对非负随机变量的,对其稍加修改,即可得到应用更为广泛的切比雪夫不等式的变形。设X是任意的随机变量,则对于∀ε > 0,有
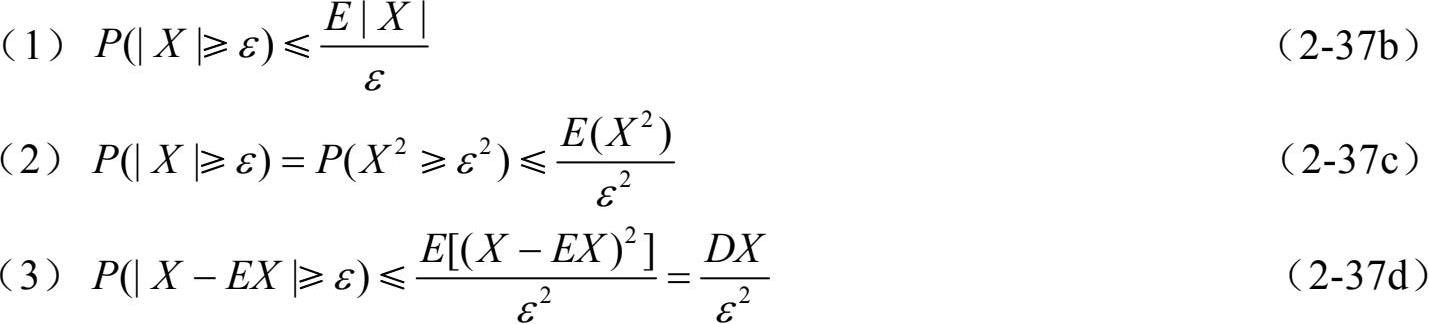
设单次伯努利试验中,事件A发生的概率为p,0≤p ≤ 1,以S n 表示前n次试验中A发生的次数,则对于∀ ε> 0,有

设X
1
, X
2
, X
3
,…, X
n
是独立同分布的随机变量序列,且数学期望E(X
i
)=μ和方差D(X
i
)= σ
2
存在,令
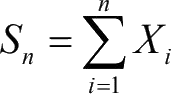 ,则对于∀ ε> 0,有
,则对于∀ ε> 0,有

证明:
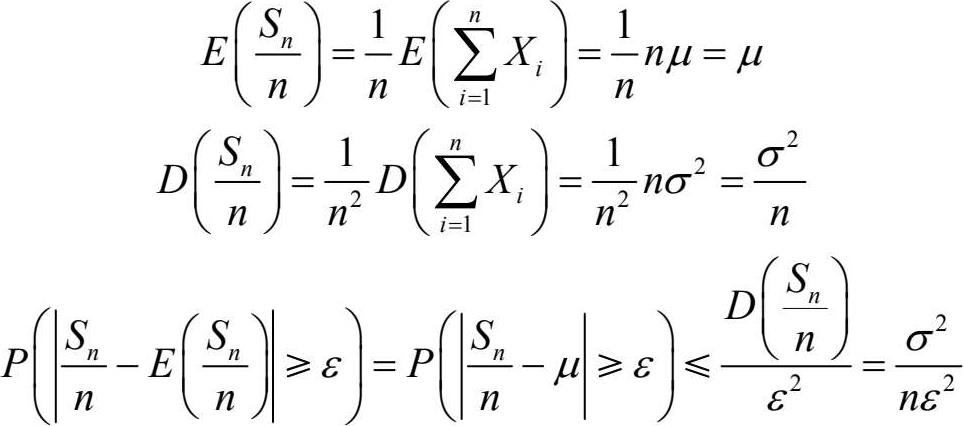
所以当n →∞时,有
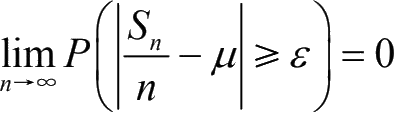 。
。
辛钦大数定律的意义是,对于独立同分布的随机变量序列X 1 , X 2 , X 3 ,…, X n ,当n →∞时,它们的算术平均值依概率收敛于它们共同的数学期望E(X i )。
设独立随机变量X 1 , X 2 , X 3 ,…, X n 的数学期望E(X 1 ), E(X 2 ), E(X 3 ),…,E(X n )和方差D(X 1 ), D(X 2 ), D(X 3 ),…,D(X n ) 都存在,且方差有公共上界K,则对于∀ ε> 0,有
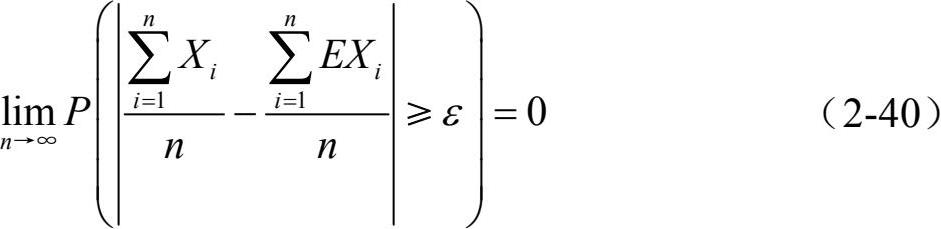
1.棣莫佛(De Moirve)-拉普拉斯(Laplace)局部极限定理
以X i 表示伯努利型随机变量,即P(X i =1)=p,P(X i =0)=q。以随机变量S n 表示n个独立的X i 之和,则S n 服从二项分布B(n, p),即
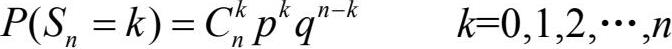
当n很大时,用二项分布计算S n 非常不便,De Moirve和Laplace给出了对S n 的估计式,即对于很大的n和S n 位于np附近时,有
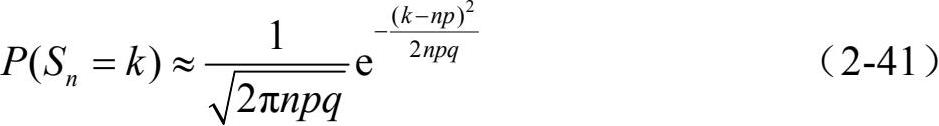
即随机变量S n 在其均值np附近近似服从正态分布N(np, npq),这个结论被称为DeMoirve -Laplace局部极限定理。该定理说明当n充分大时,大量的服从两点分布的随机变量的和S n 近似服从正态分布N(np, npq),因此我们可以用正态分布来逼近二项分布。以参数p=0.2 为例绘图 2-17 和图 2-18。
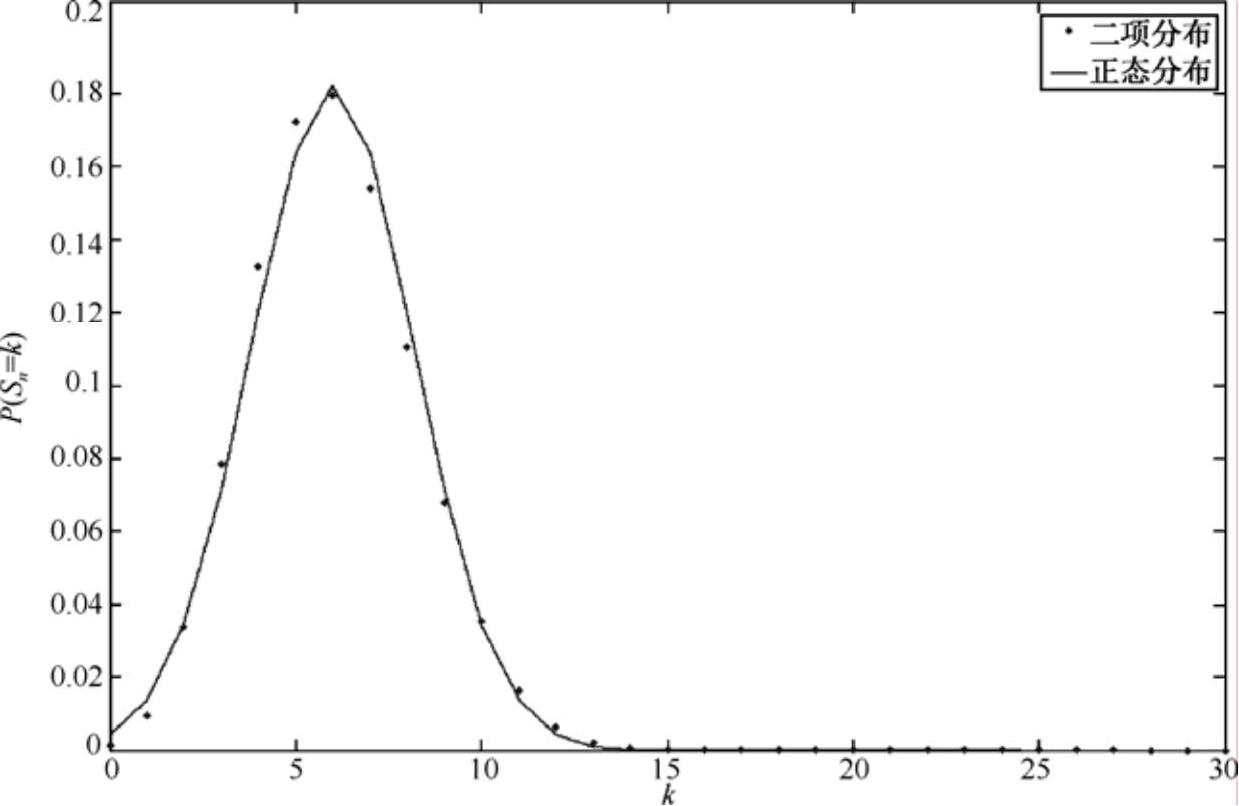
图 2-17 p=0.2,n=30 的二项分布与正态分布
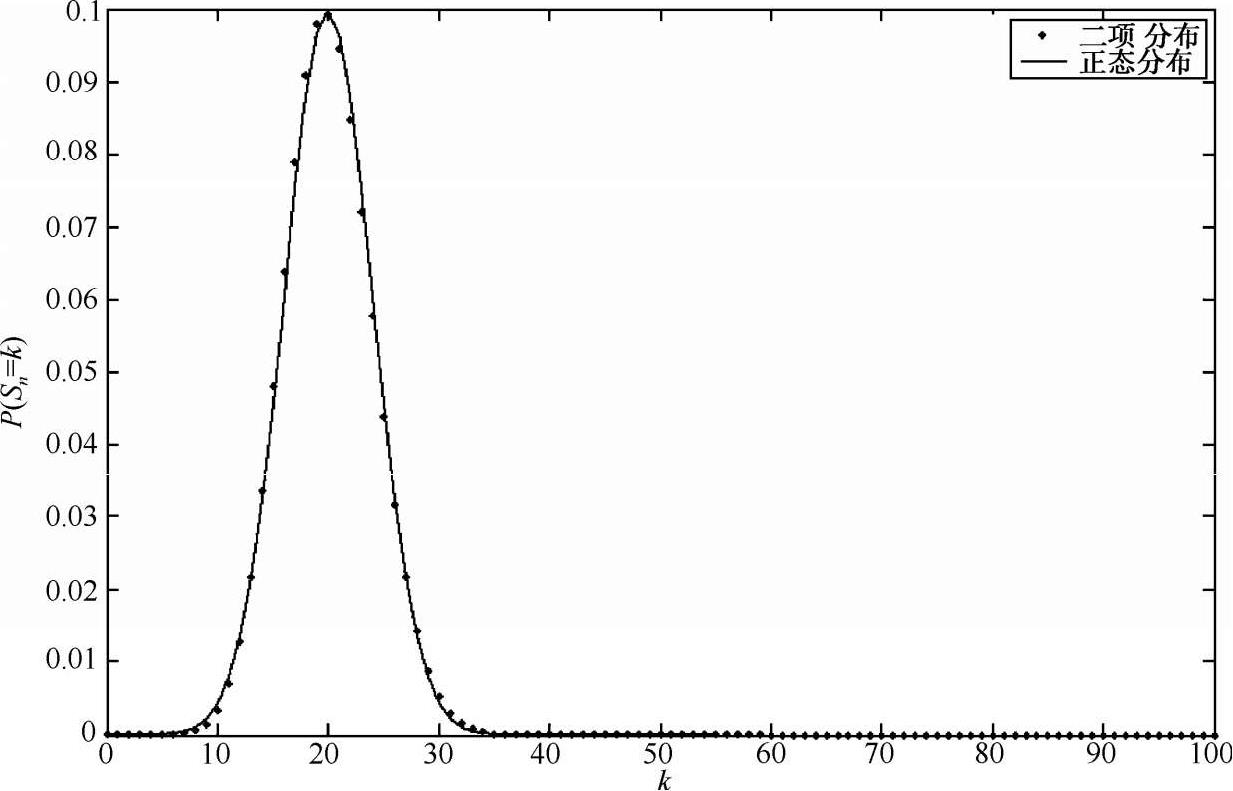
图 2-18 p=0.2,n=100 的二项分布与正态分布
设X 1 , X 2 , X 3 ,…,X n 为独立同分布的随机变量,E (X i )= μ,D (X i )= σ 2 ,则当n →∞时,S n 近似服从正态分布,即满足

设独立的随机变量X 1 , X 2 , X 3 ,…,X n ,E (X i )= μ i ,D (X i )= σ i 2 ,则
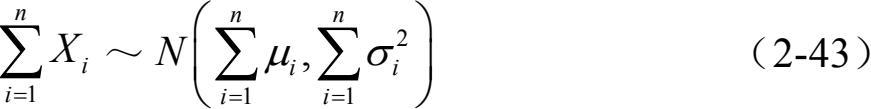
中心极限定理说明如果一个随机变量(或现实量)是大量独立的随机变量之和,其中每个分量对总量只做微小的贡献,则可以认为总量服从正态分布。