随机变量的分布函数和概率分布是对随机变量概率特征的精确、完备的描述，然而很多实际问题并不需要知道随机变量概率分布如此细致的刻画，只需要知道一些基本特征即可，这就需要引入随机变量数字特征的概念。

2.3.1 数学期望

1．离散型随机变量的数学期望

设一维离散型随机变量X的概率分布如表 2-4 所示。

定义一维离散型随机变量X的数学期望为

和式中可能是有限项取和，也可能是可列无穷多项构成的级数，根据X的取值情况决定，数学期望又叫均值。

2．连续型随机变量的数学期望

设一维连续型随机变量X的概率密度函数为f _X （x），定义其数学期望为

3．数学期望具有的性质

（1）常量的期望等于该常量，即E（C）=C。

（2）常量因子可以提到期望算符的外边，即E（CX）=CE（X）。

（3）随机变量和的期望等于各自期望的和，即E（X+Y）=E（X）+E（Y）。

（4）独立随机变量乘积的期望等于各自期望的乘积。

4．一维随机变量X的函数Y=g（X）的数学期望

5．二维随机变量（X，Y）的函数Z=g（X，Y）的期望

（1）假设二维离散型随机变量（X，Y）的联合概率分布如表 2-5 所示。

则Z=g（X，Y）的期望的计算公式为

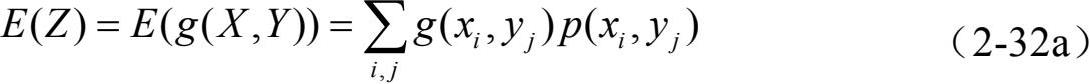
（2）假设二维连续型随机变量（X，Y）的联合概率密度函数为 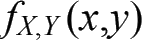，则Z=g（X，Y）的期望的计算公式为

2.3.2 矩

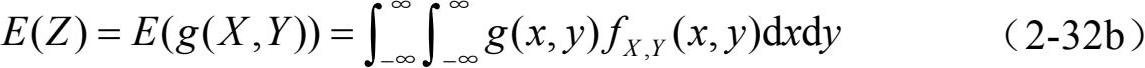
对于随机变量X，有一些特殊函数Y=g（X）的数学期望，对应着X的各种数字特征，称为矩（moment）。

（1）令 ，

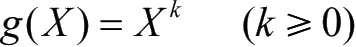则

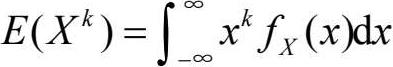
称为X的k阶原点矩。

（2）令 ，

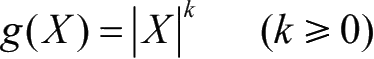则

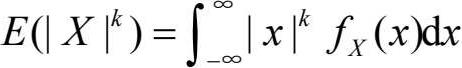
称为X的k阶绝对原点矩。

（3）令 ，

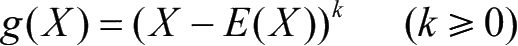则

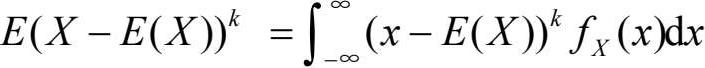
称为X的k阶中心矩。

（4）令 ，

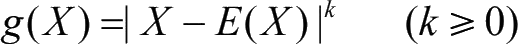则

称为X的k阶绝对中心矩。

其中，1 阶原点矩就是期望，2 阶中心矩也是一个很重要的数字特征，称为方差。

2.3.3 方差

在概率中用以描述随机变量X在其均值附近散布程度的数字特征是方差，记作D（X）或简写作DX，定义为：D （X ） =E[ （X -EX） ² ]，其中EX表示X的期望。

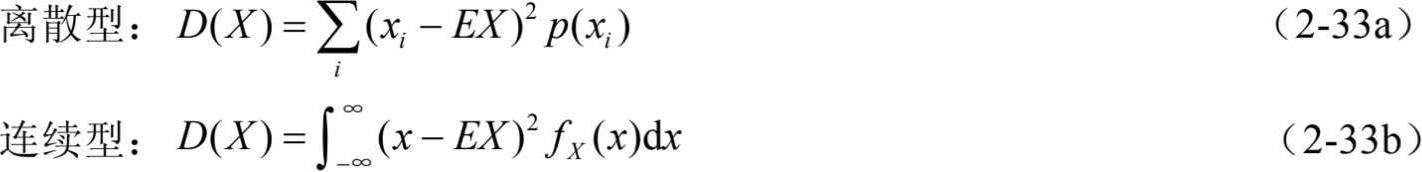
定义随机变量X的标准差为 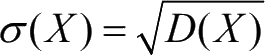。此外，

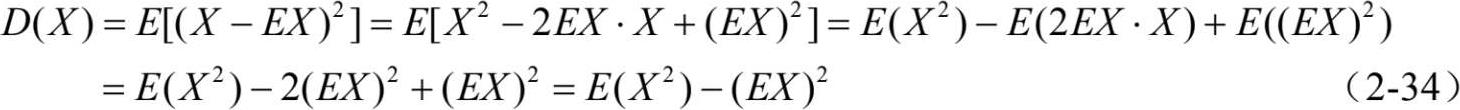
方差具有如下性质：

（1）非负性，即D（X）≥0。

（2）常量的方差为 0，即D（C）=0。

（3）设C为常量，则有D（CX）=C ² D（X），即方差算符内的常量因子提到算符外边的时候要取平方。

（4）设随机变量X，Y独立，则有

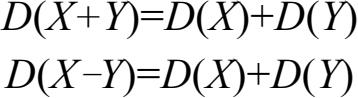
（5）方差的量纲是随机变量量纲的平方。

2.3.4 协方差和相关系数

定义二维随机变量（X， Y）的协方差为

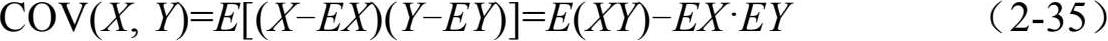
协方差也称为二阶混合中心矩。若r.v. X， Y独立，则COV（X， Y）=0，但反之不成立。COV（X， Y）=0 也被称为X， Y不相关，因此独立是不相关的充分条件而非必要条件。

协方差具有如下性质：

（1）COV（X，X）=D（X）

（2）COV（X，Y）= COV（Y，X）

（3）COV（aX，bY）= ab COV（X，Y）

（4）COV（X ₁ + X ₂ ，Y）= COV（X ₁ ，Y）+ COV（X ₂ ，Y）

（5）D（X+Y）=DX+DY+2COV（X，Y）；D（X-Y）=DX+DY-2COV（X，Y）

定义随机变量（X ， Y）的相关系数为

可见相关系数对协方差做了归一化处理，使之不依赖于原点和测量单位的选择。相关系数具有如下性质：

（1）-1≤ρ （X，Y）≤1。

（2）X， Y独立→ρ （X，Y）=0，即X，Y独立是相关系数为 0 的充分条件。

（3）| ρ |=1 当且仅当X，Y是线性相关的，即存在常数a，b（a≠0），使得Y=aX+b。 LgW9T3kUSsuem1WMZOFcJK8kxUYdxptgEMvn8qRXNNdANhwqfoTOm+OT1Zs5DS75