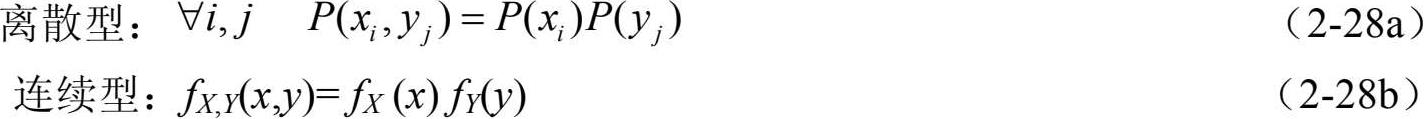定义:设
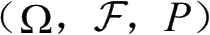 是一个概率空间,ξ( ω)是定义在基本事件空间Ω上的单值实函数,如果对于任意实数x,集合{ω:ξ(ω)≤x}都是一个事件,即
是一个概率空间,ξ( ω)是定义在基本事件空间Ω上的单值实函数,如果对于任意实数x,集合{ω:ξ(ω)≤x}都是一个事件,即
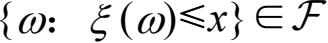
则称ξ (ω)为随机变量(random variable简记为r.v.)。
根据随机变量值域类型的不同,可以把随机变量划分为两种类型。
离散型随机变量:仅能取有限个或可列个数值,即变量的值域是离散集合。
连续型随机变量:能够取不可列个数值,即变量的值域是连续集合。
随机变量ξ (ω)取某些值(或位于某个区域)总可以映射成基本事件空间Ω的某个子集,如图 2-3 所示,所以可以通过计算该事件的概率得到ξ (ω)取这些值的概率。但在实际应用中随机变量的直观意义比样本空间Ω或事件的意义更为清晰明了,所以可以直接使用随机变量,而不必指明样本空间Ω。
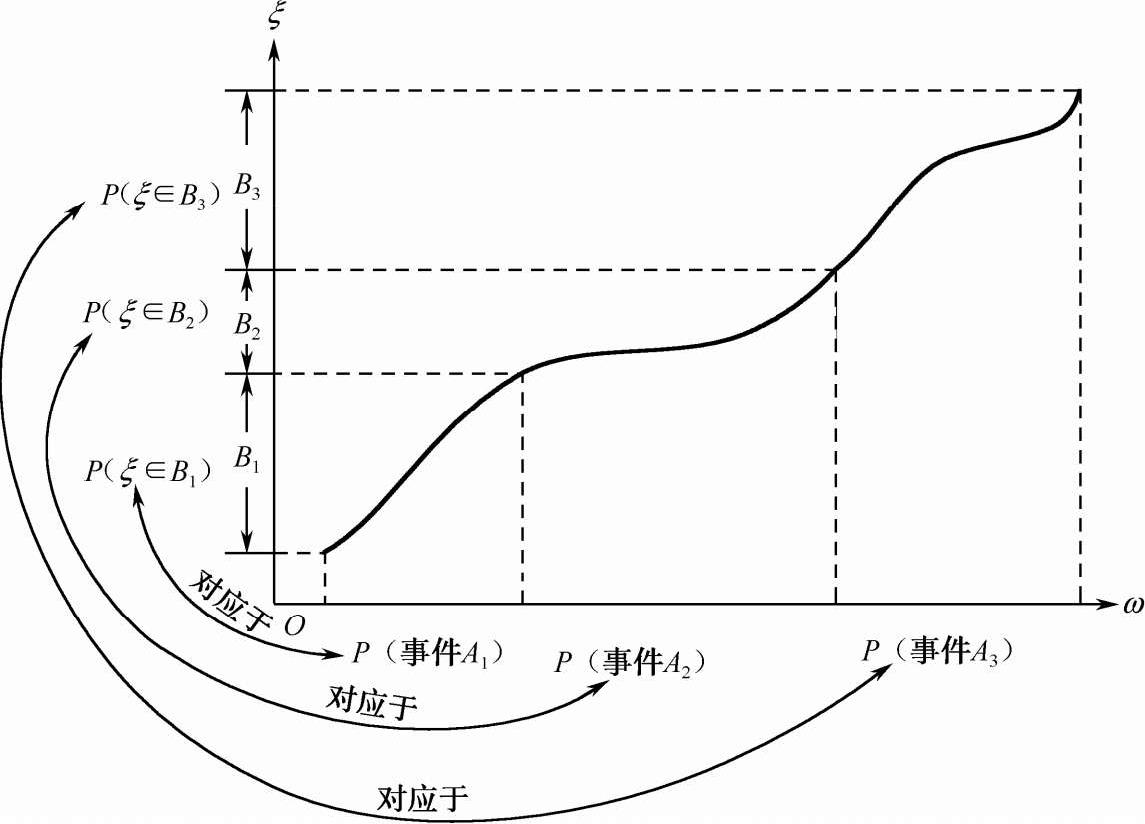
图 2-3 随机变量概率的获得
随机变量在其值域(离散型是离散集合;连续型是连续集合)内的概率分布是一个很重要的问题。离散型随机变量从有限集合或可列集合中取值,所以其概率分布总可以列成两行多列的表格(如表 2-2 所示)或图形(如图 2-4 所示)的形式。
表 2-2 离散型随机变量的概率分布

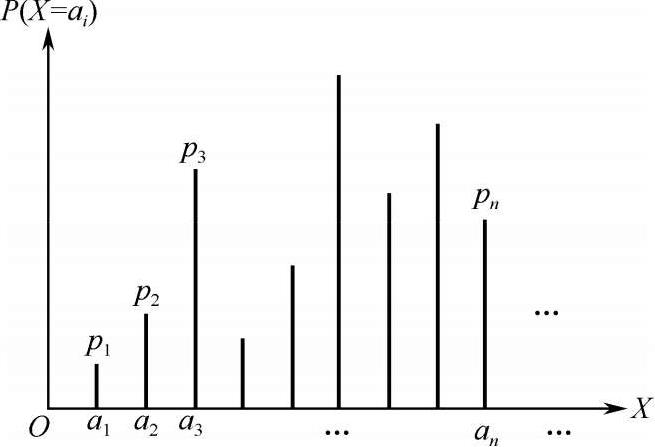
图 2-4 离散型随机变量的概率分布
离散型随机变量的概率分布应该满足:
非负性:
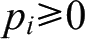
规范性:
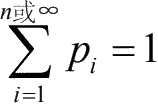
连续型随机变量X从不可列集合中取值,所以其概率分布应该是一个连续函数。对于这种情况,X等于某个单值的概率已经没有意义,只能说X位于某个区间(c, d)的概率是多少,如图 2-5 所示。
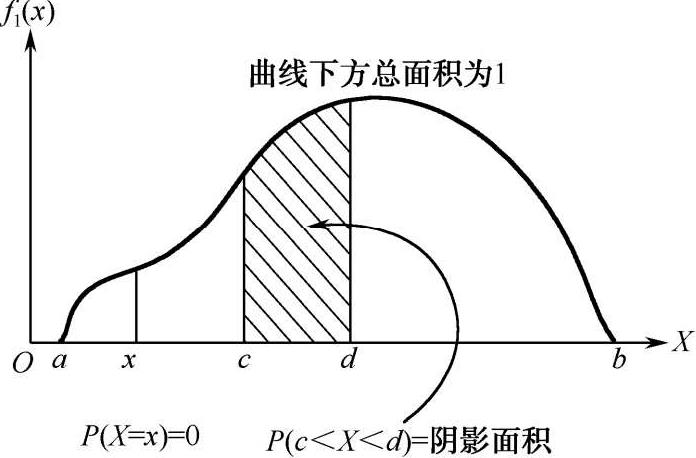
图 2-5 连续型随机变量的概率分布
图 2-5 中连续函数曲线
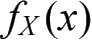 的作用类似于图 2-4 中离散的概率分布列,它清晰地反映了随机变量位于取值区间内各子区间的概率分布情况,
的作用类似于图 2-4 中离散的概率分布列,它清晰地反映了随机变量位于取值区间内各子区间的概率分布情况,
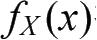 扮演的角色就好像某种物质散布在各处的密度一样,因此称为概率密度函数,简记作PDF。概率密度函数在某个子区间内取积分就是随机变量位于该子区间内的概率,即P(c<X<d) =
扮演的角色就好像某种物质散布在各处的密度一样,因此称为概率密度函数,简记作PDF。概率密度函数在某个子区间内取积分就是随机变量位于该子区间内的概率,即P(c<X<d) =
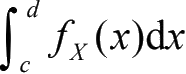 。
。
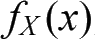 应满足:
应满足:
非负性:
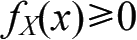
规范性:
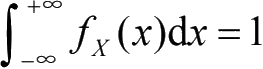
定义:对于r.v. X,称函数
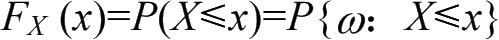 为X的分布函数或累积分布函数,简记作CDF。
为X的分布函数或累积分布函数,简记作CDF。
分布函数有如下计算公式:

分布函数具有如下性质:
(1)分布函数是单调不减函数,即对于数轴上任意的
 ,有
,有
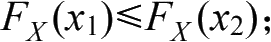
(2)分布函数的取值介于 0 和 1 之间,这是因为分布函数本身具有概率的含义;
(3)
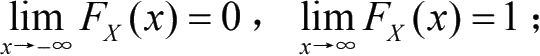
(4)分布函数
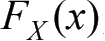 是右连续的函数,即对于数轴上任意点a,一定有
是右连续的函数,即对于数轴上任意点a,一定有
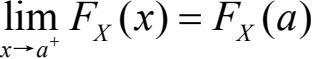
随机变量的分布函数也是对其概率分布的一种精确描述,因此应该与概率分布有着必然的联系。事实上,分布函数和概率分布是等价的、一一对应的,由概率分布可以得到分布函数,反之亦然。
对于离散型随机变量有
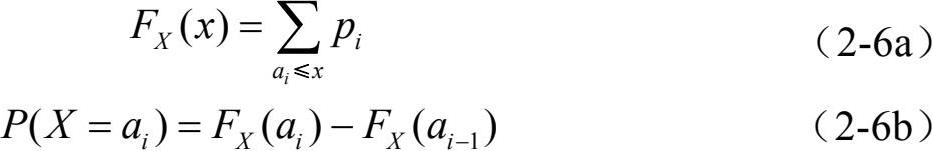
对于连续型随机变量有

1)两点分布
若随机变量X的概率分布为

其中 0<p<1,q=1-p,则称X的概率分布符合两点分布,其物理试验原型是扔硬币试验,把一面朝上记作X=0,另一面朝上记作X=1,其概率分布也可记作
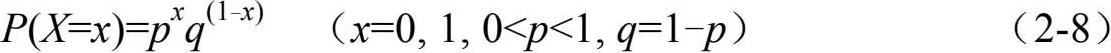
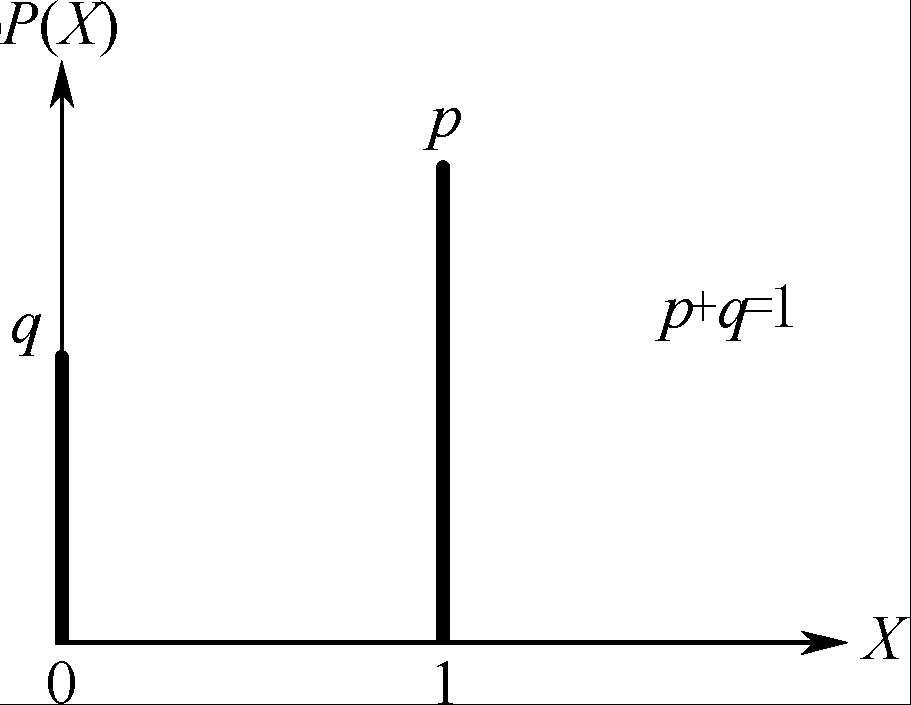
图 2-6 两点分布
如图 2-6 所示,可见,两点分布用于描述只有两种结果的随机试验,这种概率分布虽然简单,却是构成很多其他分布的重要基础。
2)二项分布
假设在单次随机试验(如打靶试验)中,成功(击中)的概率为p,失败(脱靶)的概率为q=1-p。如果把这个试验独立地进行n次,则根据独立性并应用组合分析不难计算,在n次试验中成功k次的概率为
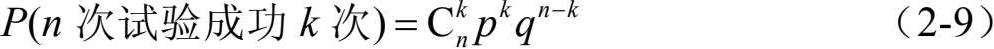
如果以r.v. X表示n次试验中成功的次数,则X的概率分布为

称r.v. X的概率分布为二项分布,记作
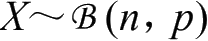 。显然,X的可能取值为 0,1,2,…,n,且X的概率分布为
。显然,X的可能取值为 0,1,2,…,n,且X的概率分布为
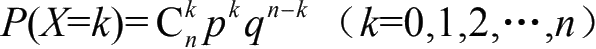 ,如图 2-7 所示。
,如图 2-7 所示。
3)几何分布
在打靶试验中,假设单次打靶击中的概率为p,脱靶的概率为q = 1- p,持续射击,直到射中为止,以r.v. X表示射击次数,则X的概率分布为
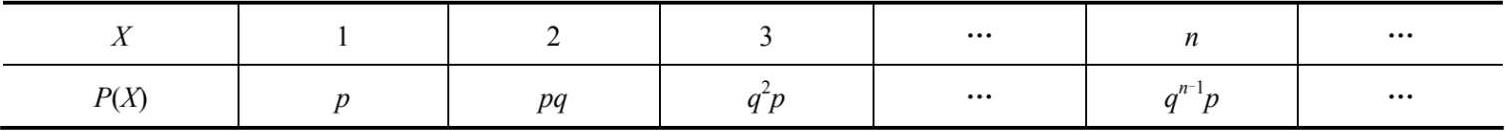
即
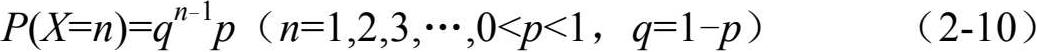
称r.v. X的这种分布为几何分布。取参数p=0.4 的几何分布如图 2-8 所示。
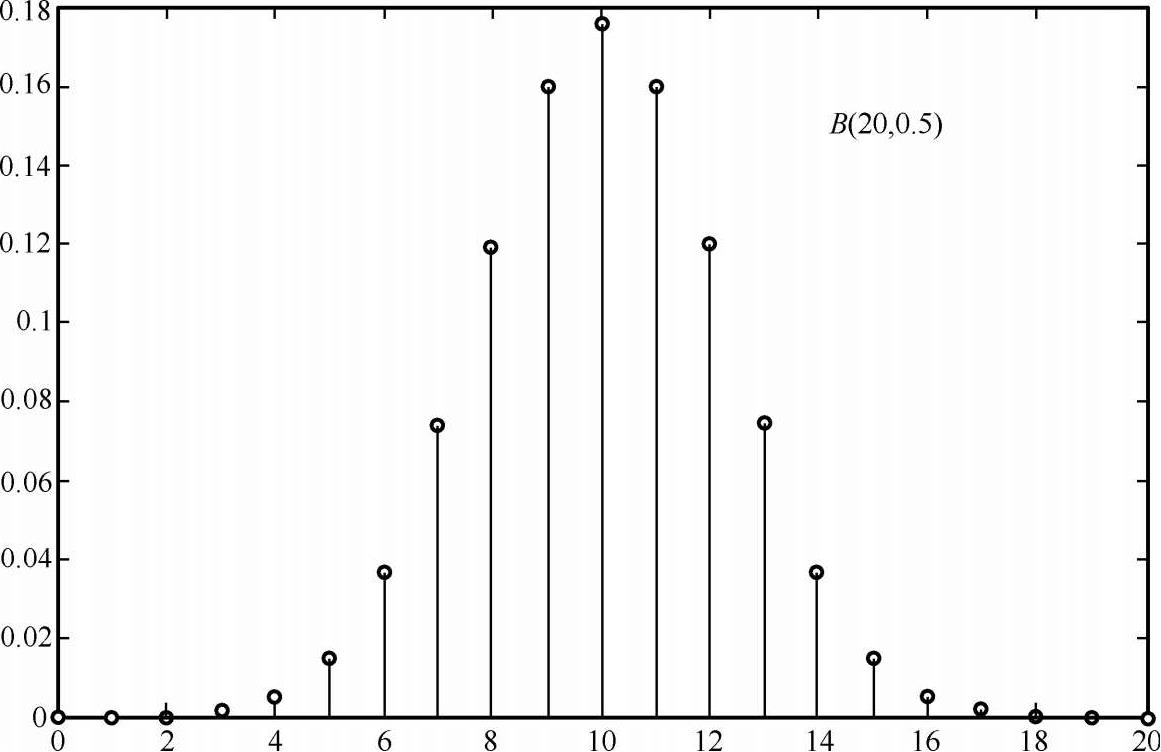
图 2-7 二项分布
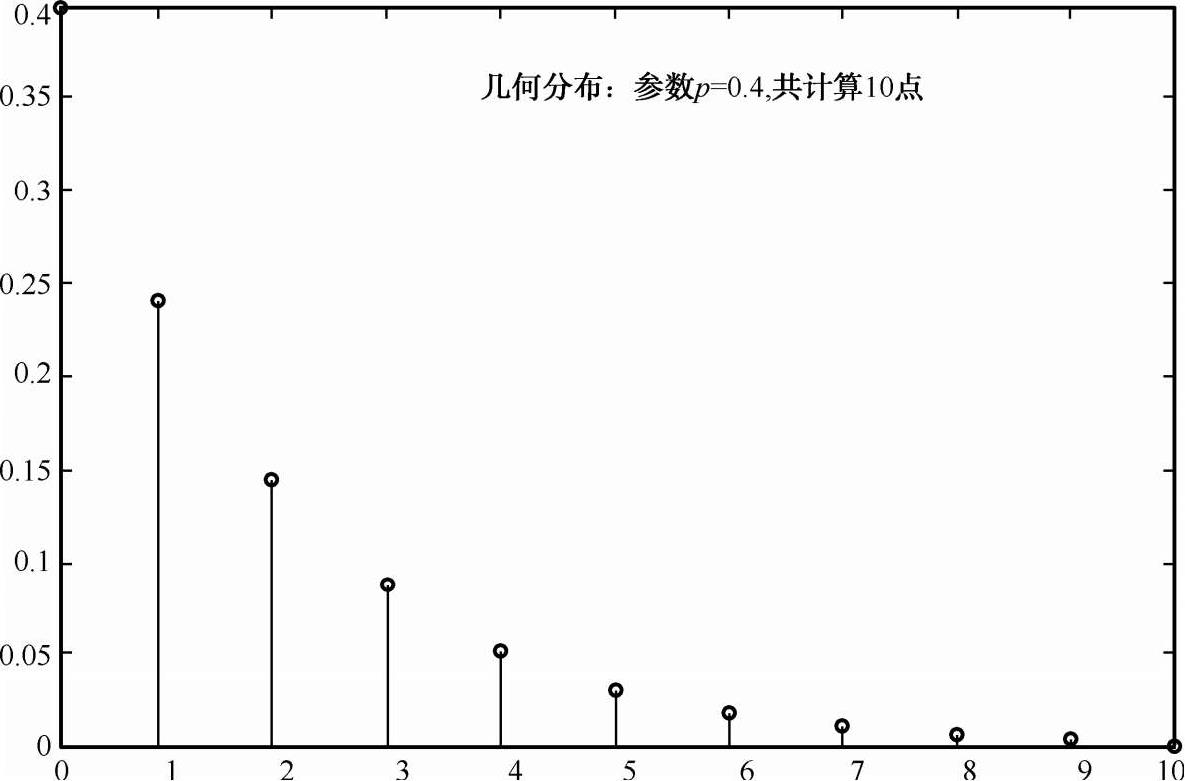
图 2-8 几何分布
4)超几何分布
假设袋子里有N个形状相同的球,其中有M个红球,N-M个黑球,从中任意抽取n个球,以r.v. X表示抽得的红球的数目,则X的概率分布为
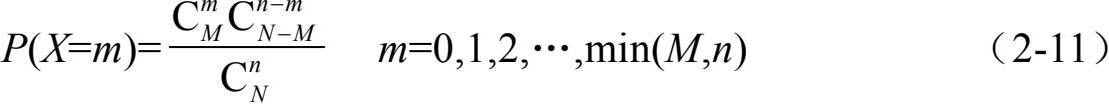
称X的分布为超几何分布,记作X~H(n,N,M)。取参数N=100,M=10,n=20 的超几何分布如图 2-9 所示。
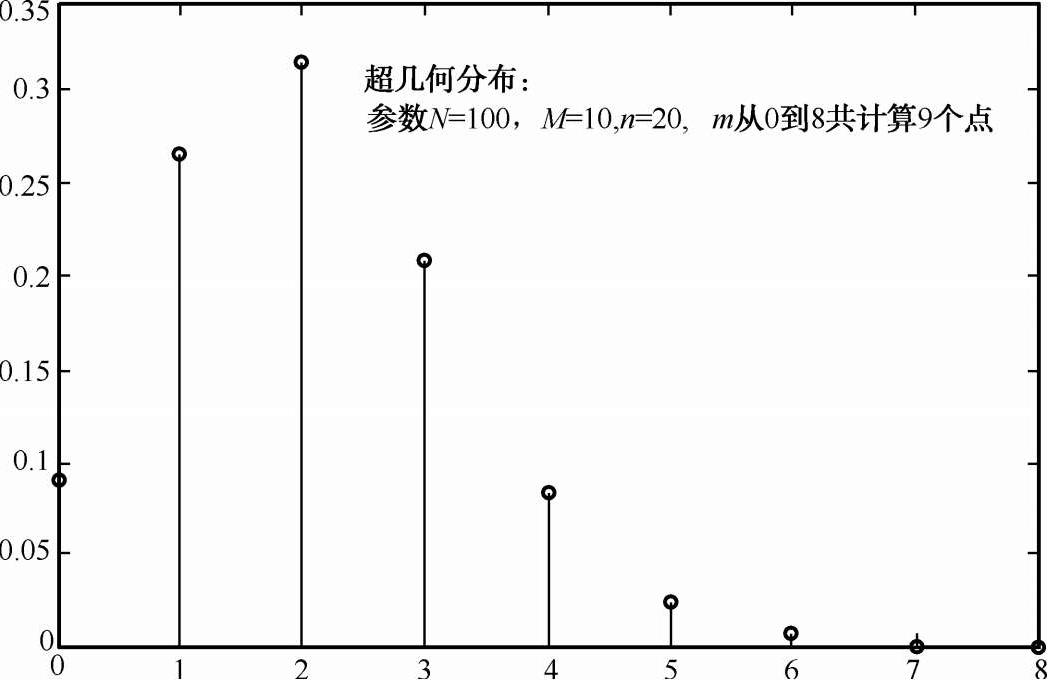
图 2-9 超几何分布
5)泊松分布
泊松分布是一种很重要的离散型概率分布。称概率分布
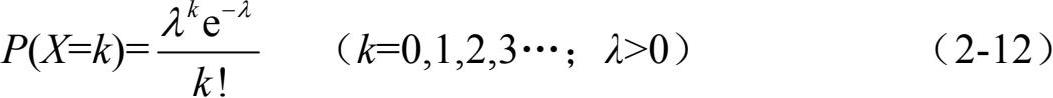
为泊松分布。取参数λ=5 的泊松分布如图 2-10 所示。
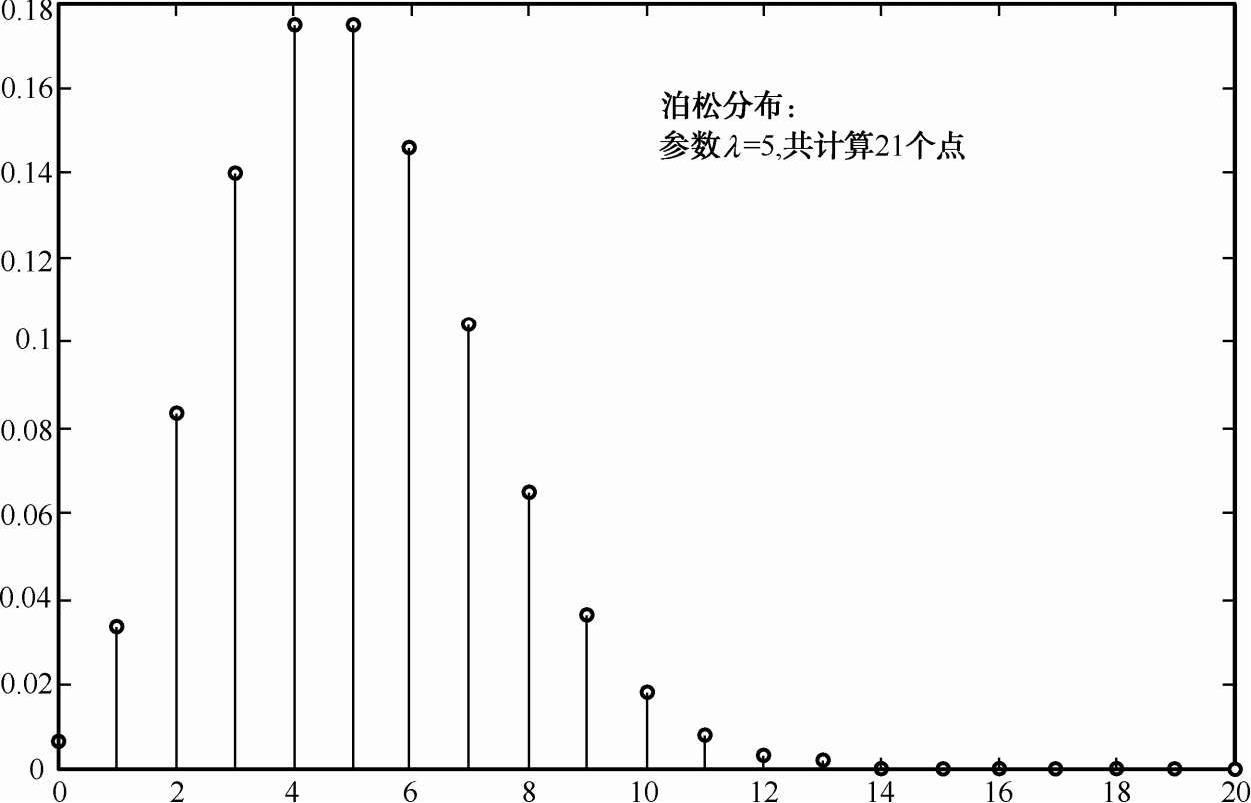
图 2-10 泊松分布
泊松分布是二项分布列的极限分布,或者说可以用泊松分布来逼近二项分布,这个性质被概括为泊松定理。
泊松定理:设有一系列n逐渐增大的二项分布
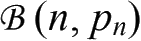 ,其中参数n和p
n
满足
,其中参数n和p
n
满足
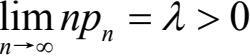
则对于任意的非负整数k,有
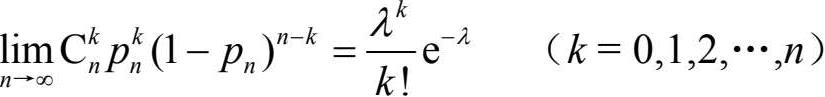
泊松分布还是对物理世界完全随机性的恰当的数学描述,因此泊松分布(更广泛意义上应称为泊松过程)又称纯随机或完全随机分布(完全随机过程)。这种随机分布的本质特征是统计独立性,即各个点在空间中的分布是彼此独立、互不影响的,泊松分布正是这种完全随机性的必然结果。排队论是研究排队或拥塞现象的规律的一门学科,在该理论中电话呼唤、顾客到达常被建模为泊松分布,称为泊松流(图 2-11)。

图 2-11 顾客到达服务台相当于泊松流
需要说明的是,在泊松分布公式中,λ的作用相当于泊松流中点分布的密度,λ越大,则点越密集。如果想统计t时间内到达服务台的客户数,假设也用X表示,则公式应修改为

连续型随机变量的分布函数和概率密度函数是连续函数,最常见的连续型随机变量的分布为均匀分布、指数分布和正态分布。
1)均匀分布
均匀分布的概率密度函数为
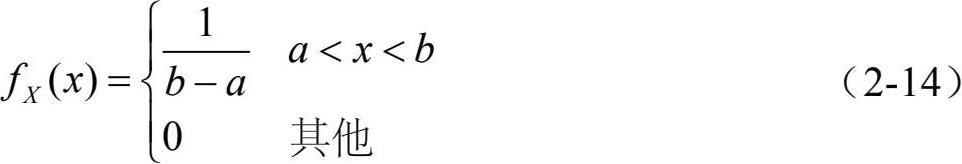
2)指数分布
指数分布的概率密度函数和分布函数分别为

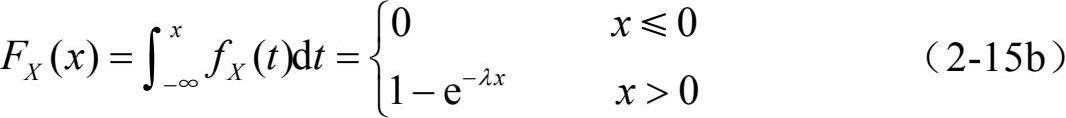
其中,λ>0 为常数。λ=1 的指数分布的概率密度函数和分布函数如图 2-12 所示。
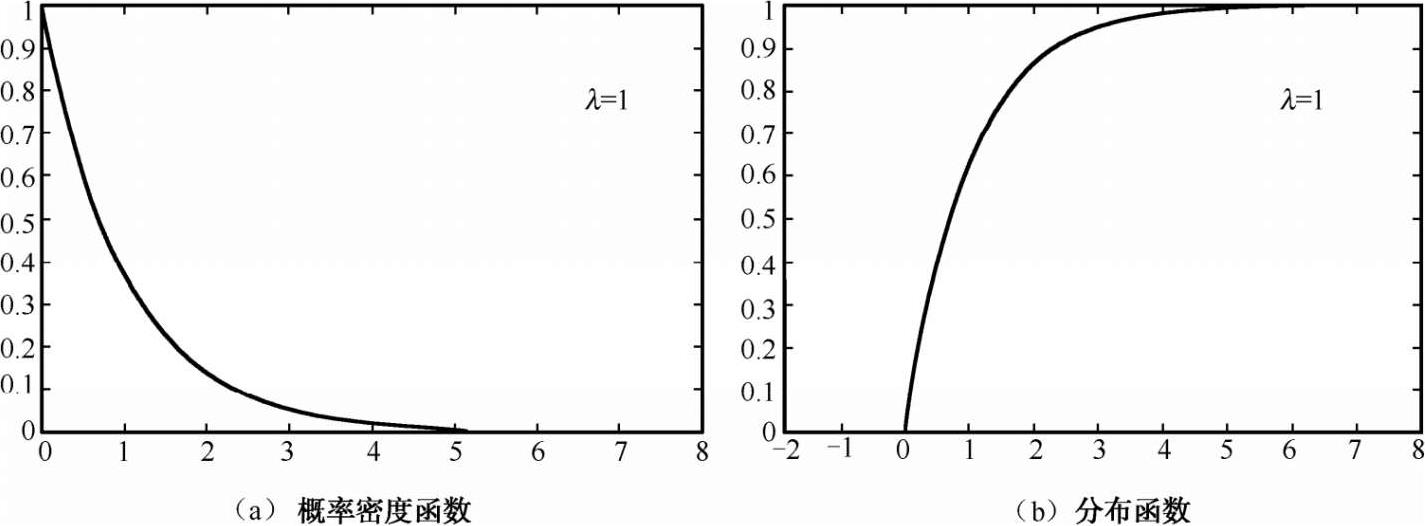
图 2-12 指数分布
指数分布与泊松分布有着密切关系,事实上,在泊松流中,事件点之间的间隔T如果看做是随机变量,是服从指数分布的,如图 2-13 所示。

图 2-13 泊松流中点的间隔服从指数分布
证明:以r.v. T表示相继两个事件点的间隔,显然T是连续型随机变量,其分布函数为
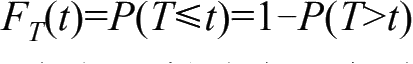 ,其中P(T>t)表示在时间段t内没有新的事件点到达的概率。根据泊松分布,在时间段t内有k个点到达的概率为
,其中P(T>t)表示在时间段t内没有新的事件点到达的概率。根据泊松分布,在时间段t内有k个点到达的概率为
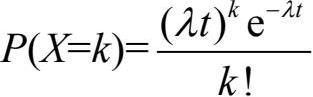
所以,在时间段t内没有新的事件点到达的概率应为
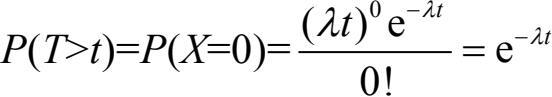
由此可得,
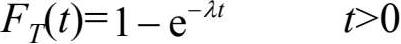
这正是指数分布的分布函数。
3)正态分布
正态分布在概率论中占据着核心的位置,其概率密度函数为
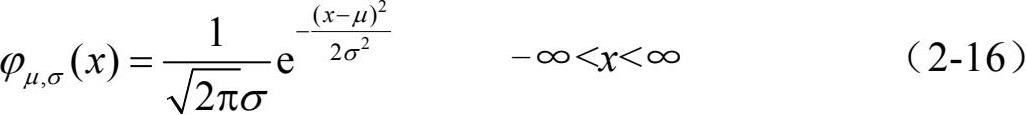
其中,μ和σ > 0 为常数,工程应用中也常称之为高斯分布,记作
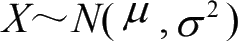 。特别地,当μ = 0且 σ
2
=1时,称这种正态分布为标准正态分布,记作X~N(0,1),其概率密度函数为
。特别地,当μ = 0且 σ
2
=1时,称这种正态分布为标准正态分布,记作X~N(0,1),其概率密度函数为
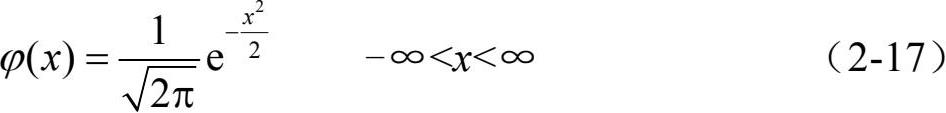
标准正态分布的概率密度函数如图 2-14 所示。
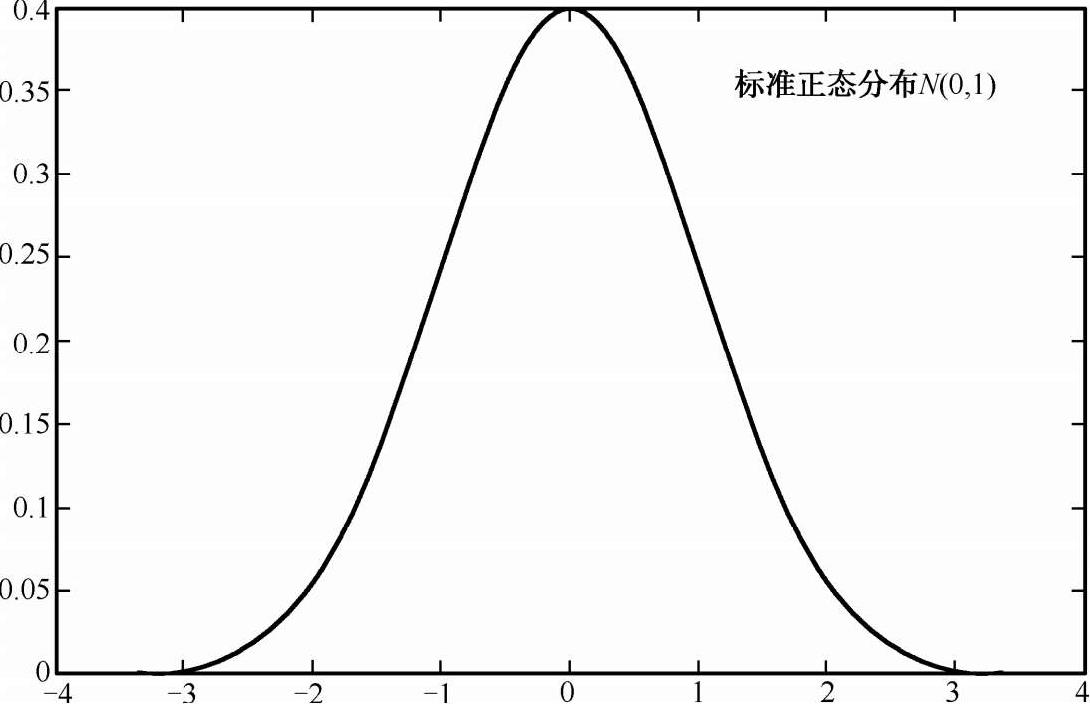
图 2-14 标准正态分布的概率密度函数
标准正态分布N(0,1)的分布函数为
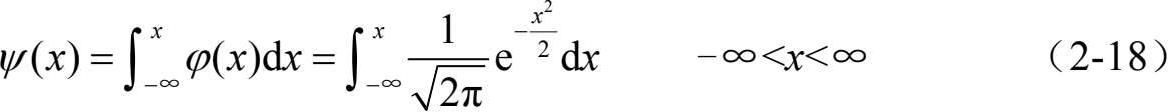
ψ (x)如图 2-15 所示。
ψ (x)具有如下性质:
(1)ψ (-∞ )=0;ψ (∞ )=1
(2)ψ (-x )=1- ψ(x)
(3)ψ (0)=0.5
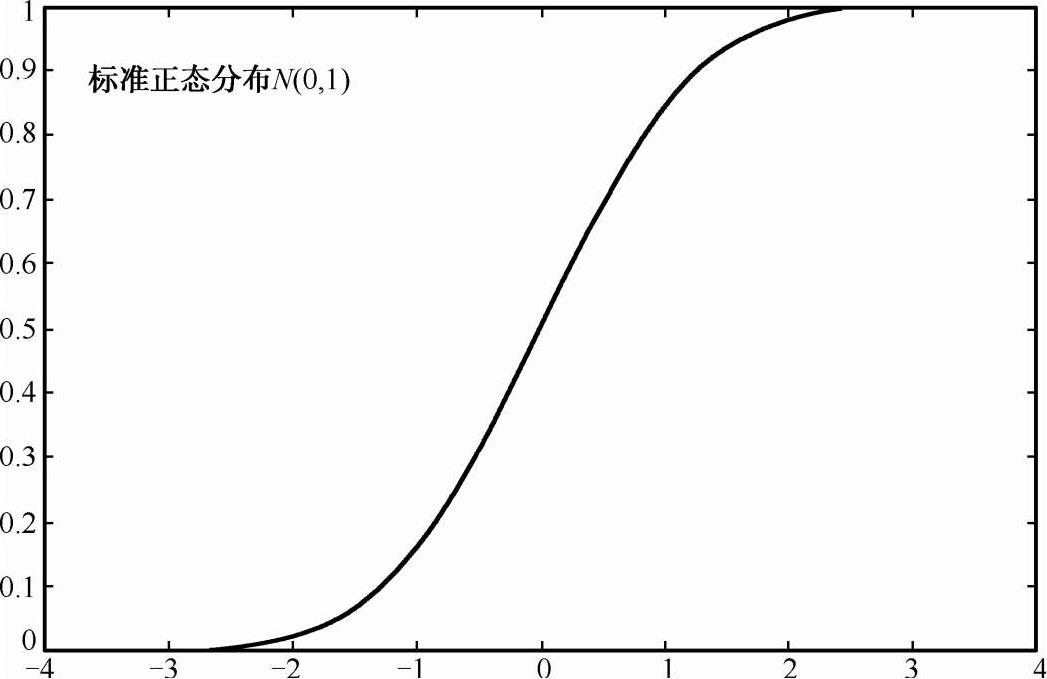
图 2-15 标准正态分布的分布函数
在概率论中,很多实际问题需要用多个随机变量来描述,如打靶击中点的坐标(X,Y)、掷两颗色子的结果(X 1 , X 2 )。这种由多个随机变量构成的变量组称为随机矢量或随机向量,其中随机变量的个数称为维数。由于随机矢量是由随机变量构成的,所以也有离散型和连续型之分。
二维离散型随机变量的概率分布可以列成如表 2-3 所示的形式。
表 2-3 二维离散型随机变量的概率分布
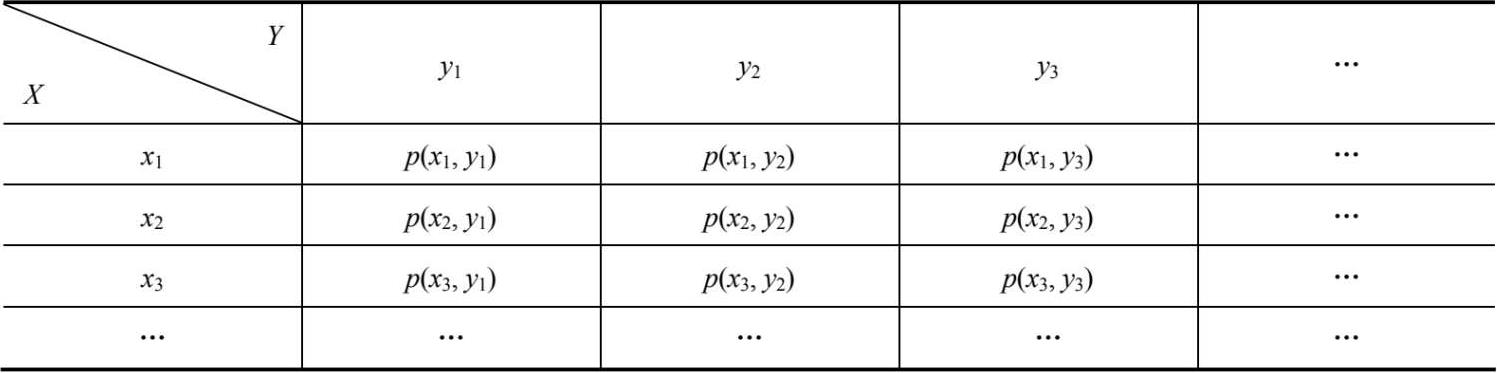
表中概率项可以是有限多个或可列无穷多个,这个概率分布表称为二维离散型随机变量的联合分布。二维离散型随机变量的概率分布也要满足非负性和规范性。
非负性:
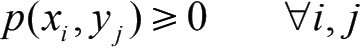
规范性:
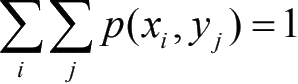
二维离散型变量(X, Y)的联合分布函数定义为
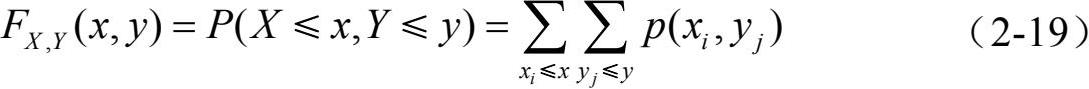
由二维离散型变量(X, Y)的联合分布可以很容易得到每个分量X、Y各自的概率分布,称其为二维离散型变量(X, Y)的边缘分布,由联合分布计算边缘分布应用如下公式:
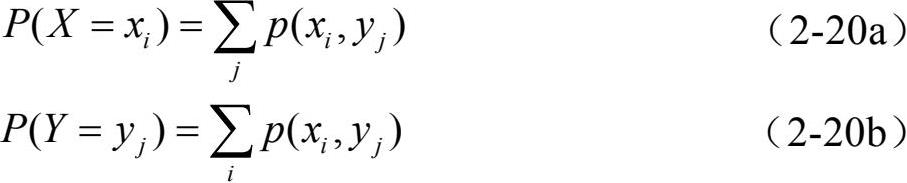
二维连续型随机变量的概率分布是由其联合概率密度函数f X ,Y(x,y)来表征的(如图 2-16 所示)。f X ,Y(x,y)需要满足:
非负性:
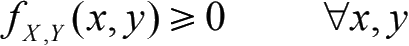
规范性:
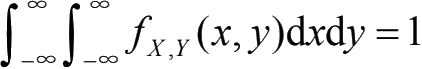
点(X, Y)落在x-y平面上任意区域D内的概率由二重积分给出:
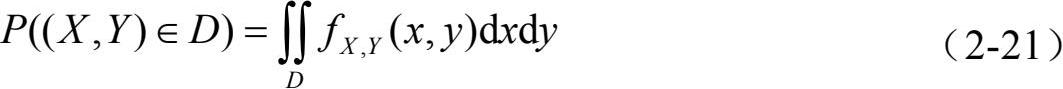
二维连续型变量(X, Y)的联合分布函数定义为
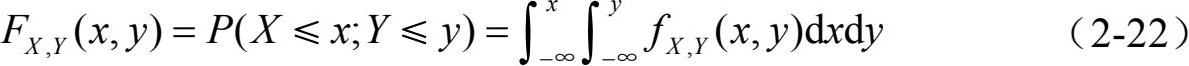
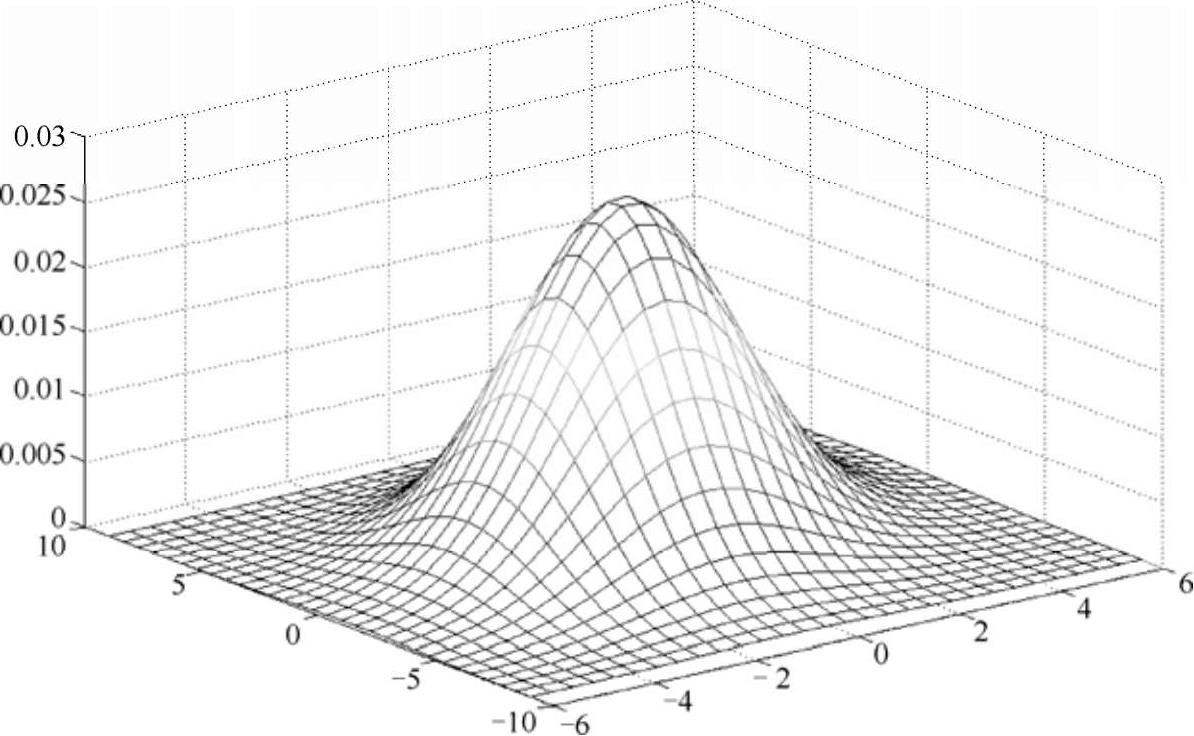
图 2-16 二维连续型随机变量的联合概率密度函数
由二维连续型随机变量的联合分布可以求其边缘分布。
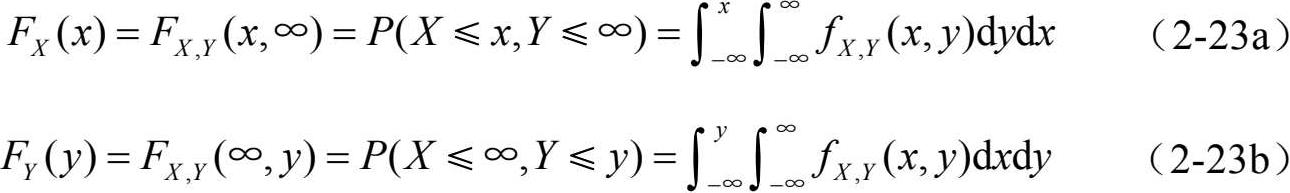
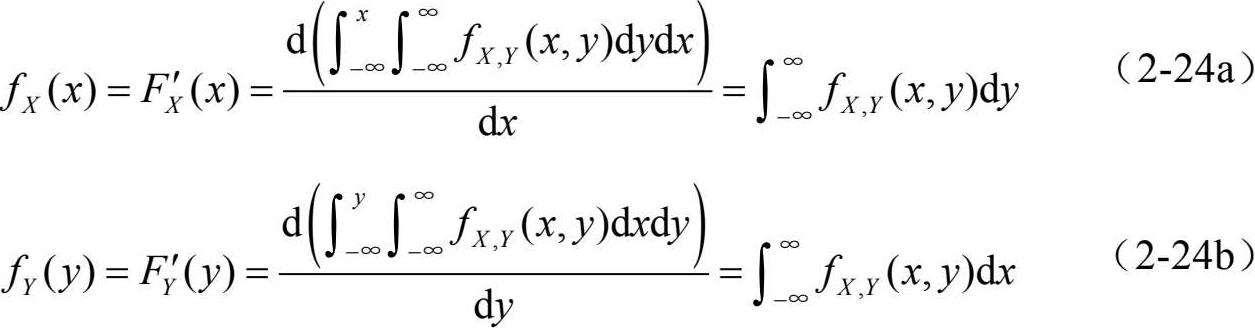
从事件的条件概率出发可以得到随机变量条件分布的概念。下面的讨论又将区分为离散和连续两种类型。
定义:设(X, Y)是二维离散型随机变量,若P(Y=y j )>0,则称
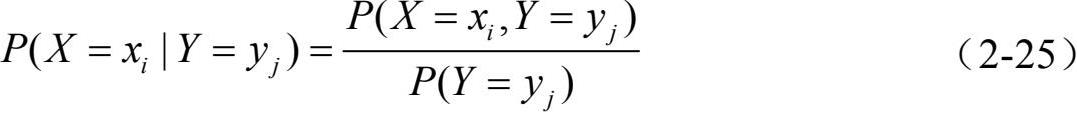
为在条件
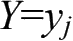 下随机变量X的条件分布。
下随机变量X的条件分布。
定义:设(X, Y)是二维连续型随机变量,其联合概率密度函数为
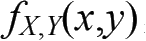 边缘概率密度函数为
边缘概率密度函数为
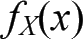 和
和
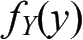 ,则当f
Y
(y)>0 时,称函数
,则当f
Y
(y)>0 时,称函数

为在条件Y=y下随机变量X的条件概率密度函数。
两个随机变量X, Y独立意味着它们的取值对彼此没有影响,其数学表现形式是(X, Y)的联合分布等于X, Y各自边缘分布的乘积。
(1)从分布函数看,联合分布函数等于边缘分布函数的乘积,即

(2)从概率分布看