





非色散介质材料中的电磁场能量密度由下式给出:
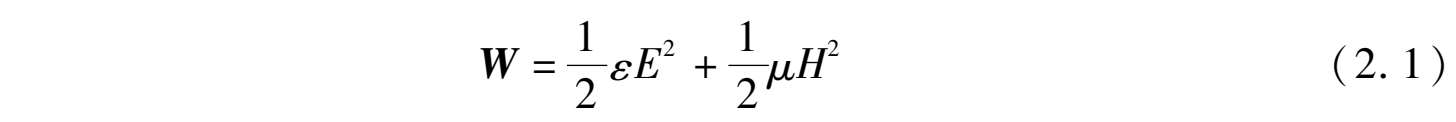
假如左手介质是非色散的,根据式(2.1),由于ε<0,μ<0则其中的电磁场能量密度W<0;那么,当电磁波由外部进入左手介质区域时,区域中存储的电磁能量会由正值变为负值,即无源的左手介质将会对外输出能量,这是违背能量守恒定律的,可见左手介质必然具有色散特性。色散的左手介质中的电磁能量密度具有如下形式:
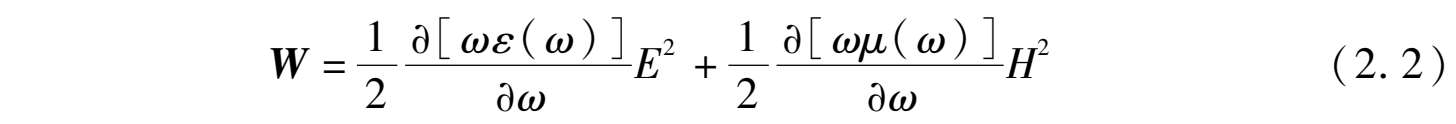
其中,ε(ω)和μ(ω)满足
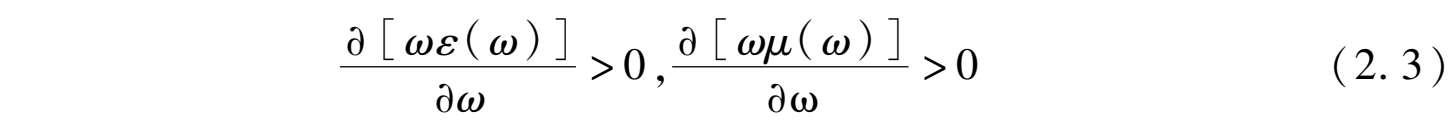
根据式(2.3),对左手介质有
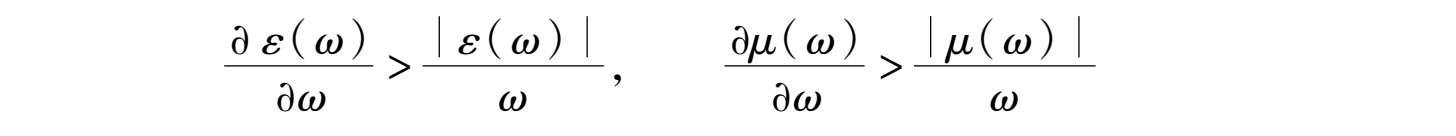
可见左手介质是强色散介质。左手介质的色散特性一直是受到关注的研究问题 [1,2] 。
D.R.Smith从左手介质中的面电流源辐射场的因果性问题出发,直观地论述了左手介质的色散特性 [3] ,这里作简要介绍。如图2.1所示,假设在空间中填充有介电常数ε,介电常数μ的均匀介质,在x=x 0 平面有均匀分布的z方向的电流源。
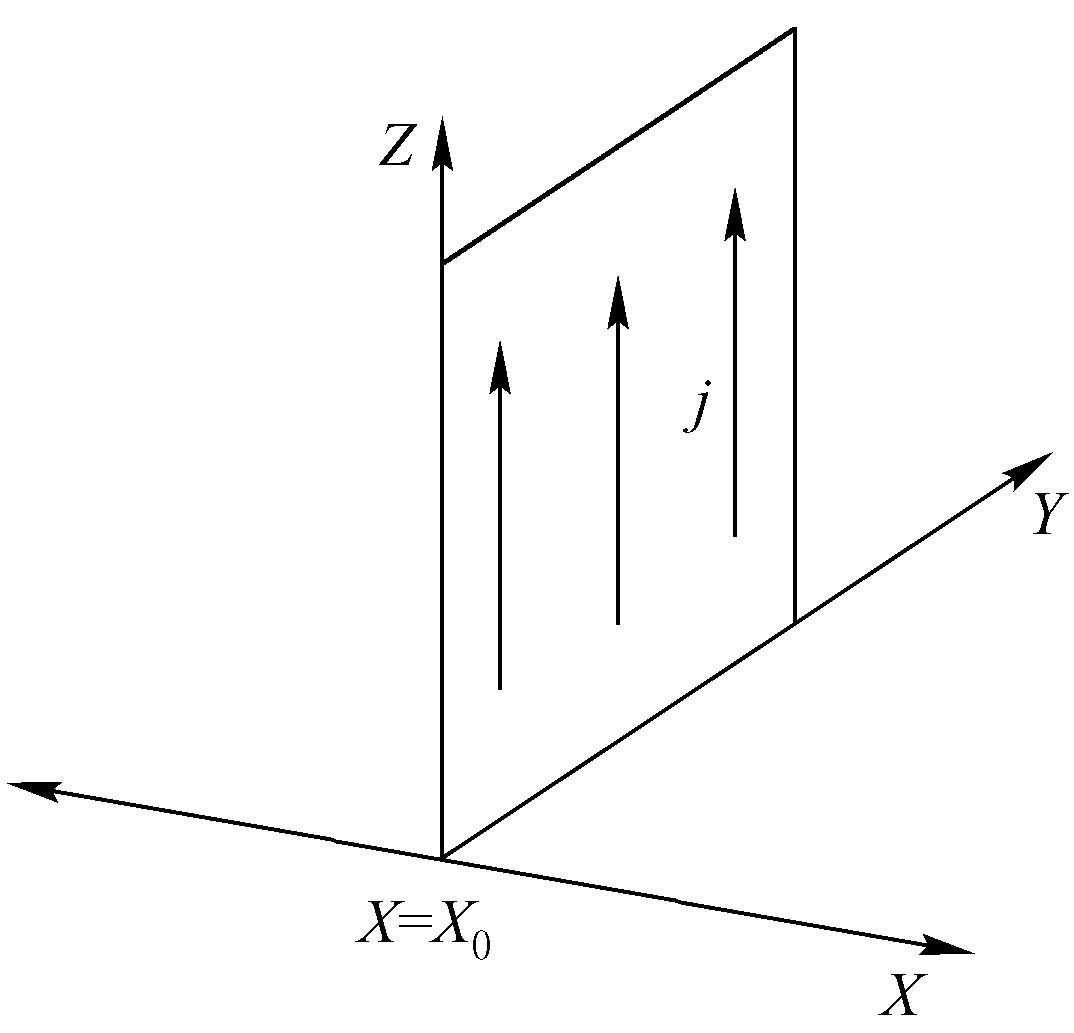
图2.1 均匀介质中的面电流源
设面电流是频率为ω,密度为j 0 (ω)的时谐源,即
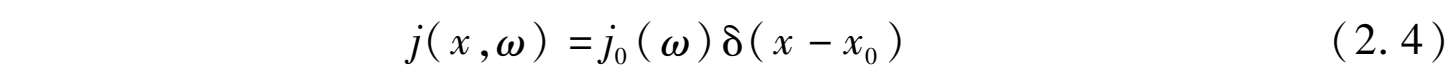
对应的一维电场波方程
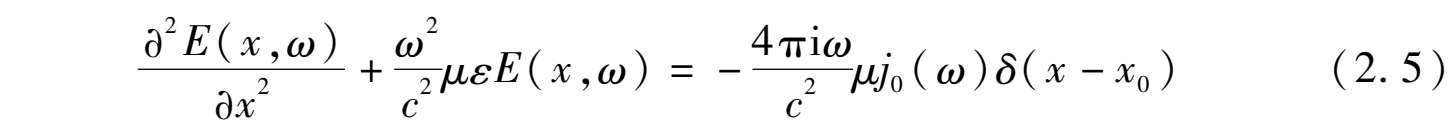
的解为
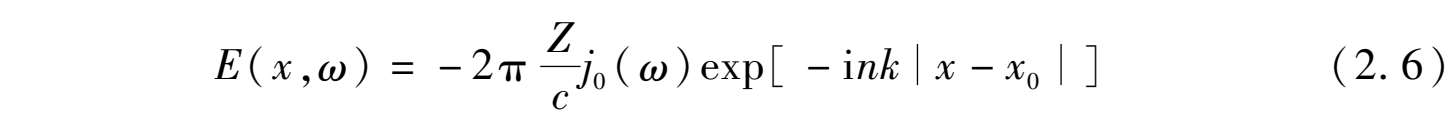
其中n
2
=με,Z=
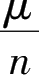 。单位面积电流源对场做的功为:
。单位面积电流源对场做的功为:
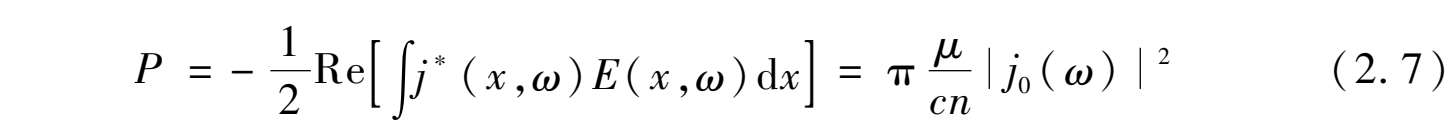
无论是右手介质还是左手介质,源对场都是做正功。对于普通右手介质,μ>0,则要求n>0。而左手介质μ<0,要满足P>0,n=n L (脚标L表示左手介质)必须为负值。
若位于x=x 0 的面电流源是任意时变电流源
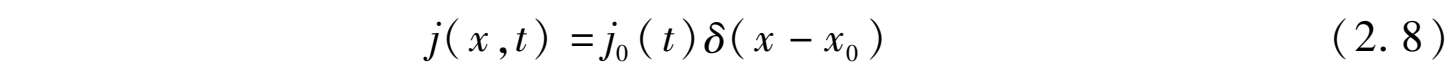
由它激励的电磁场可以通过对式(2.6)进行逆傅里叶变换得到:
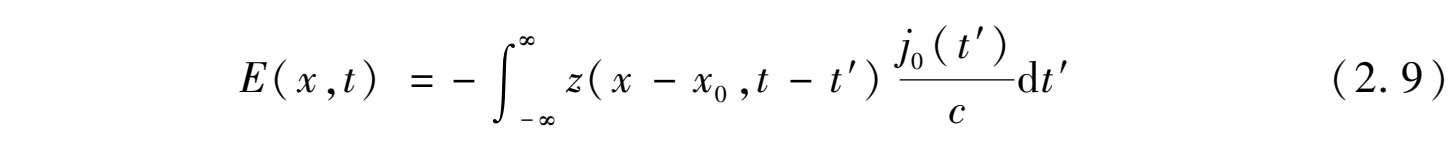
其中,
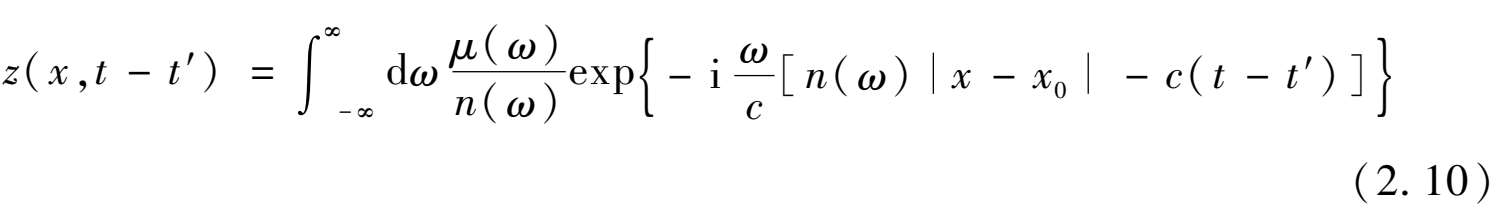
假设填充介质是非色散的,其介电常数和磁导率均为常数,式(2.10)可简化为
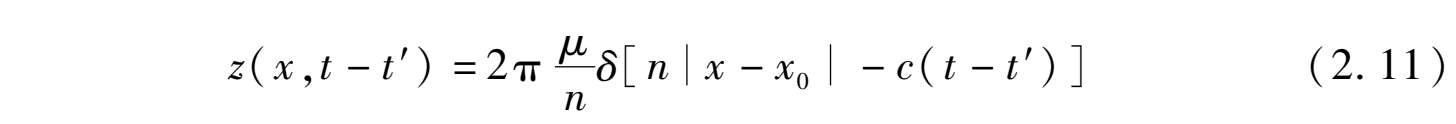
对于右手介质,n>0,当t<t′时,z(x,t-t′)=0;而对于左手介质,n=n L <0,则当t>t′时,z(x,t-t′)=0。可见因果律要求左手介质必须具有色散特性,非色散的左手介质是不满足因果律要求的。R.W.Ziolkowski等人通过对脉冲在左手介质中传播的分析也证实了,介质的色散特性对脉冲形状的改变是电磁信号在左手介质材料中传播不违反因果律的保障 [4] 。
利用周期的人工结构实现的左手介质,决定介质电磁特性的因素除单个微结构单元对电磁场的响应外,微结构单元间存在的多重耦合在一些情况下也是不可忽略的。考虑单元间存在的多重耦合,左手介质不仅是时间色散的,还具有空间色散特性。微结构单元虽然称为“人工的原子或分子”,但其几何尺寸远大于原子、分子的几何尺寸,因此单元间耦合对电磁场的影响将导致介质的空间色散。异向介质的空间色散特性在有限尺寸的人工电磁材料的设计中已受到关注 [5] 。