





使用矩阵进行运算的第一步是生成矩阵。本小节将介绍学习和工作中常用的MATLAB矩阵生成函数。
【功能简介】 生成不同维度和不同数据类型的零矩阵。
【语法格式】
1.B=zeros([m n p ...])或B=zeros(m,n,p,…)
生成m×n×p×…全零数组。
2.B=zeros([m,n])或B=zeros(m,n)
生成m×n全零矩阵。
3.B=zeros(n)
生成n×n全零矩阵。
4.B=zeros(size(A))
生成与A大小相同的全零矩阵。
5.B=zeros(…,type)
生成指定数据类型的零矩阵。可接受的参数有'double'、'single'、'int8'、'uint8'、'int16'、'uint16'、'int32'、'uint32'、'int64'和 'uint64'等。
【实例3.1】 生成二维和三维零矩阵。

【实例分析】 class函数用于显示变量的数据类型。
【功能简介】 生成单位矩阵。
【语法格式】
1.Y=eye([m,n])或Y=eye(m,n)
生成m×n单位矩阵。
格式变体:
■ Y=eye(n):生成n×n单位矩阵。
2.Y=eye(size(A))
生成与A大小相同的单位矩阵。
【实例3.2】 生成单位矩阵。

【实例分析】 eye函数生成的矩阵不一定是方阵。
【功能简介】 生成魔方矩阵。魔方矩阵是一个n×n方阵,n≥3,矩阵由1~n 2 中的数构成。矩阵每行、每列和两条对角线上的数之和是一样的,且等于sum(1:n^2)/n。如果n小于3,则返回的不是魔方矩阵。
【语法格式】

生成n×n魔方矩阵。
【实例3.3】 生成3×3魔方矩阵。

【实例分析】 矩阵的行、列、对角线之和都等于15。
【功能简介】 生成不同维度和不同数据类型的全1矩阵。
【语法格式】
1.Y=ones([m n p ...])或Y=ones(m,n,p,…)
生成m×n×p×…全1数组。
2.Y=ones([m,n])或Y=ones(m,n)
生成m×n全1矩阵。
3.Y=ones(n)
生成n×n全1矩阵。
4.Y=ones(size(A))
生成与A大小相同的全1矩阵。
5.Y=ones(…,type)
生成指定数据类型的全1矩阵。可接受的参数有'double'、'single'、'int8'、'uint8'、'int16'、'uint16'、'int32'、'uint32'、'int64' 和'uint64'等。
【实例3.4】 生成一个三维全1矩阵。

【实例分析】 ones函数的调用格式与zeros函数相同。
【功能简介】 生成线性等分向量。
【语法格式】
1.y=linspace(a,b,n)
在闭区间[a,b]上生成n个线性等分点。
2.y=linspace(a,b)
相当于y=linspace(a,b,100),在闭区间[a,b]上生成100个线性等分点。
【实例3.5】 分别用冒号运算符和linspace函数生成线性等分向量。
【实例分析】 冒号运算符能直接控制数字间距,linspace函数能直接控制向量长度。
【功能简介】 生成对数等分向量。
【语法格式】
1.y=logspace(a,b,n)
在闭区间[10 a ,10 b ]上生成n个对数等分点。
2.y=logspace(a,b)
相当于y=logspace(a,b,50),在闭区间[10 a ,10 b ]上生成50个对数等分点。
【实例3.6】 对数等分向量与线性等分向量的比较。

执行结果如图3-1所示。
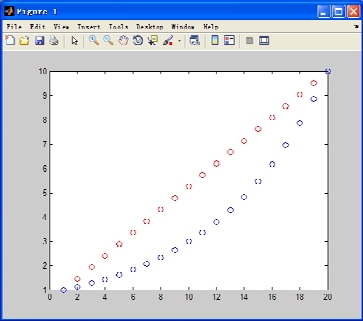
图3-1 对数等分向量与线性等分向量。
【实例分析】 红色坐标点为线性等分向量,蓝色坐标点为对数等分向量。
【功能简介】 生成[0,1]区间上均匀分布的随机矩阵。
【语法格式】
1.rand([m n p ...])或rand(m,n,p,…)
生成m×n×p×…均匀分布矩阵。
2.rand([m,n])或rand(m,n)
生成m×n均匀分布矩阵。
3.rand(n)
生成n×n均匀分布矩阵。
4.rand(size(A))
生成与A大小相同的均匀分布矩阵。
5.rand
相当于rand(1),只产生一个随机数。
6.rand(…,'double')或rand(…,'single')
生成指定数据类型的随机数矩阵。
【实例3.7】 利用rand函数生成100~150之间的随机数。

【实例分析】 rand是MATLAB中十分常用的函数。
【功能简介】 生成正态分布的随机矩阵。
【语法格式】
1.randn([m n p ...])或randn(m,n,p,…)
生成m×n×p×…正态分布随机矩阵。
2.randn([m,n])或randn(m,n)
生成m×n正态分布随机矩阵。
3.randn(n)
生成n×n正态分布随机矩阵。
4.randn(size(A))
生成与A大小相同的正态分布随机矩阵。
5.randn
相当于randn(1),只产生一个正态分布的随机数。
6.randn(…,'double')或randn(…,'single')
生成指定数据类型的正态分布随机数矩阵。
【实例3.8】 利用randn函数生成随机数矩阵。

执行结果如图3-2所示。
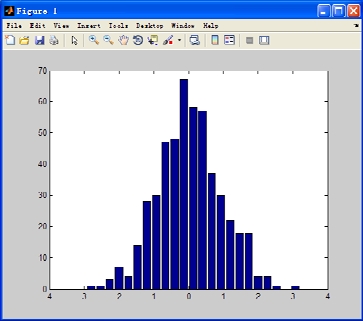
图3-2 随机数在各区间的数量分布。
【实例分析】 变量x用于统计各区间中随机数的个数。图3-2直观地显示了randn产生正态分布随机数的功能,由于数字是随机的,每次运行产生的结果都不相同,但多次实验后基本接近正态分布概率密度函数的形状。
【功能简介】 生成一定范围内整数的随机排列。
【语法格式】

生成1~n之间整数的无重复随机排列。
【实例3.9】 生成1~10之间整数的随机排列。

【实例分析】 randperm可以产生1~n之间的随机顺序。
【功能简介】 cat函数通过连接多个矩阵的方式生成多维矩阵。
【语法格式】
1.C=cat(dim,A,B)
沿着dim所指定的维度连接数组A与数组B。例如,当dim为1时,沿着列的方向连接A与B,即C=[A;B]。当dim为2时,沿着行的方向连接A与B,即C=[A,B]。
2.C=cat(dim,A1,A2,A3,A4,…)
沿着dim所指定的维度连接数组A1、A2、A3、A4等。
【实例3.10】 通过实例理解参数dim的作用。


【实例分析】 dim取1、2、3时,函数分别将a和b排列在列、行和页面中。
【实例3.11】 用cat函数从结构体数组中提取某一域,构成新的数组。

【实例分析】 data为结构数组,cat函数从中提取int域中的数,构成新的数值数组,便于计算。
【功能简介】 希尔伯特矩阵是一种数学变换矩阵,正定,且高度病态,MATLAB中用hilb函数生成希尔伯特矩阵。
【语法格式】

生成n阶希尔伯特矩阵,其元素为H(i,j)=1/(i+j-1)。
【实例3.12】 生成一个3阶希尔伯特矩阵。

【实例分析】 病态矩阵中,任何一个元素发生一点变动,整个矩阵的值和逆矩阵都会发生巨大变化,病态程度和阶数相关。
【功能简介】 由于希尔伯特矩阵中,数据的微小抖动都会引起逆矩阵的巨大变化,因此采用一般方法无法求希尔伯特矩阵的逆矩阵。MATLAB有专门的invhilb函数解决这个问题。
【语法格式】

生成n阶希尔伯特逆矩阵。
【实例3.13】 生成一个3阶希尔伯特逆矩阵。

【实例分析】 用invhilb函数才能可靠地求出希尔伯特矩阵的逆矩阵。
【功能简介】 生成帕斯卡矩阵。二项式展开的系数随n的增大组成一个三角形,称为杨辉三角形。由杨辉三角形表组成的矩阵称为帕斯卡(Pascal)矩阵。
【语法格式】
1.A=pascal (n)
生成n阶Pascal矩阵。返回的结果是对称、正定的矩阵,其元素由Pascal三角形组成,它的逆矩阵中所有元素都是整数。
2.A=pascal(n,1)
生成由下三角形排列的Cholesky系数组成的n阶Pascal矩阵,它的逆矩阵是它本身。
3.A=pascal(n,2)
生成pascal(n,1)的转置和交换形式。
【实例3.14】 生成3阶Pascal矩阵。

【实例分析】 容易看出,c=fliplr(b')。
【功能简介】 生成托普利兹(Toeplitz)矩阵。矩阵中,除第一行与第一列外,其他所有元素都与左上角相邻位置的元素相等,即T(i,j)=T(i-1,j-1)。
【语法格式】
1.T=toeplitz(c,r)
生成非对称托普利兹矩阵,将c作为第一列,r作为第一行,若c(1)与r(1)不相等,则使用c(1)作为矩阵的第一个元素,同时打印一条警告信息。
2.T=toeplitz(r)
生成对称的托普利兹矩阵,将r作为第一行与第一列。
【实例3.15】 用给定的向量c、r生成非对称托普利兹矩阵。

【实例分析】 当c与r第一个元素不相等时,采用向量c的第一个元素,忽略r的第一个元素。
【功能简介】 生成友矩阵。
【语法格式】

u为多项式向量,A返回多项式u的友矩阵。A的第一行元素为-u(2:n)/u(1),即u的第2~n个元素除以第1个元素再取相反数。矩阵A的特征值是多项式的根。
【实例3.16】 生成多项式(x-1)(x+2)(x-3)=x 3 -2x 2 -5x+6的友矩阵。

【实例分析】 eig函数求出矩阵的特征值,可以看出A的特征值等于多项式的根。
【功能简介】 生成Hankel矩阵。Hankel矩阵的构成方式是:先指定第一列和最后一行,矩阵中其他所有元素都与其左下角相邻位置的元素相等,即H(i,j)=H(i+1,j-1)。
【语法格式】
1.H=hankel(c,r)
生成非对称的Hankel矩阵。第一列元素为c,最后一行元素为r,若c的最后一个元素与r的第一个元素不相等,交叉位置的元素取c的最后一个元素。
2.H=hankel(c)
生成对称的Hankel矩阵。第一列元素为c,次对角线下方所有元素均为零。
【实例3.17】 给定向量c、r生成Hankel矩阵。
【实例分析】 除第一列与最后一行外,其余元素都等于其左下方相邻的元素。
【功能简介】 生成以输入元素为对角线元素的矩阵。
【语法格式】

生成以a,b,c,d,…为对角线元素的矩阵。
【实例3.18】 生成以1.5、2.5、3.5为对角线元素的矩阵。

【实例分析】 除对角线外,其余元素均为零。
【功能简介】 生成Wilkinson特征值测试矩阵。
【语法格式】

生成n阶特征值测试矩阵,它是一个对称的三对角矩阵。
【实例3.19】 生成4阶特征值测试矩阵。

【实例分析】 Wilkinson特征值测试矩阵是一个三对角矩阵。
【功能简介】 生成最小二乘增广矩阵。
【语法格式】

S返回一个稀疏、对称的非正定方阵,S=[c*I,A;A',0],c为残留比例因子,I为单位矩阵。函数的功能是求解一个最小二乘问题:
min(norm(b-A*x))
norm函数用于求第二范式,如向量[1,1]的第二范式为sqrt(1 2 +1 2 )=1.4142。最小二乘问题可以表述为:
r=b-A*x
S*[r/c;x]=[b;0]
【实例3.20】 生成一个最小二乘增广矩阵。
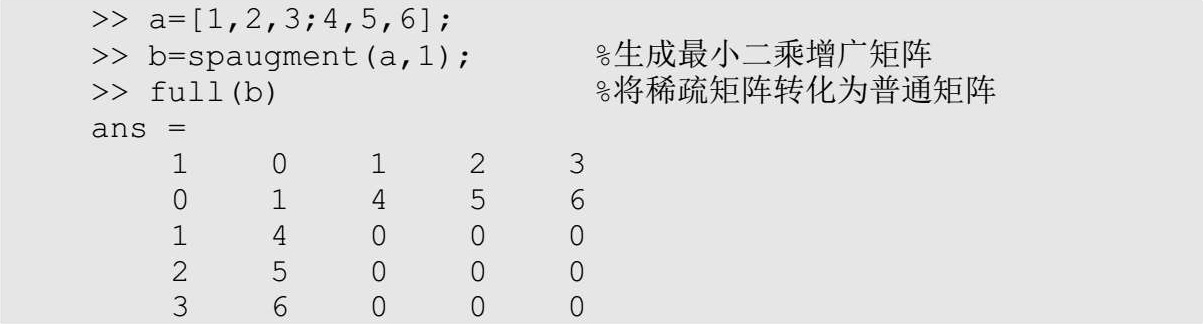
【实例分析】 关于最小二乘计算的详细信息,请读者查看相应的帮助文档。