




在19世纪末,物理学界普遍存在着一种乐观情绪,认为物理学大厦已经建立,对于物理现象的本质已经有了基本全面的认识,后辈的物理学家只需做一些修补工作。物理学家们陶醉于17世纪建立起来的力学体系、19世纪建立起来的电磁学、热力学及统计物理学,直到被开尔文(Kelvin)爵士一篇名为“19世纪的乌云笼罩着热和光的动力学理论”的报告所震动。报告中指出经典物理学的两个未能圆满解释的基本问题,被比喻为物理学悬浮着两朵乌云。“第一朵乌云”是指迈克尔逊—莫雷(Michelson-Morley)实验结果和以太漂移说相矛盾;“第二朵乌云”则指观测到的物理比热总是低于经典物理学中能量均分定理给出的值,其中尤以黑体辐射理论出现的“紫外灾难”最为突出。经典物理学经历着前所未有的巨大危机,急需新的理论来补充,相对论和量子力学就是在这种背景下进入了历史舞台的中心。爱因斯坦(Einstein)提出的狭义相对论,改变了牛顿(Newton)力学中的绝对时空观,指明了牛顿力学的适用范围,即只适用于速度v远小于光速的物质的运动。量子力学则涉及物质运动形式和规律的根本变革,经典物理学只适用于描述一般宏观条件下物质的运动,而对于微观世界和一定条件下的某些宏观现象,则只有在量子力学的理论上才能说明。本节从19世纪末经典力学遇到的困难出发,简要介绍量子力学的形成过程。
1895年,基尔霍夫(Kirchhoff)定量地研究了物体对光的吸收和辐射效应,发现所有物体发射光与吸收光的能力之比是一常数,这种能力只与物体自身的温度和光的波长有关,而与物体的材料及其结构无关。随后,基尔霍夫引入了黑体的概念,所谓黑体是指在任何温度下都能全部吸收到达其上的一切辐射的理想吸收体。可见,黑体的吸收能力达到最大,因此随后的研究大都集中在黑体的辐射能力上。
1896年,维恩(Wien)提出了一个辐射能量分布的半经验公式:

式中,E(ν)dν表示在频率范围(ν,ν+dν)和单位体积中温度为T的黑体辐射能量,c 1 与c 2 是两个参数。但后来的实验发现维恩公式只适用于较高频率和较低温度时的情形,如图1.1所示,在较高频率时维恩公式与实测值符合得较好。
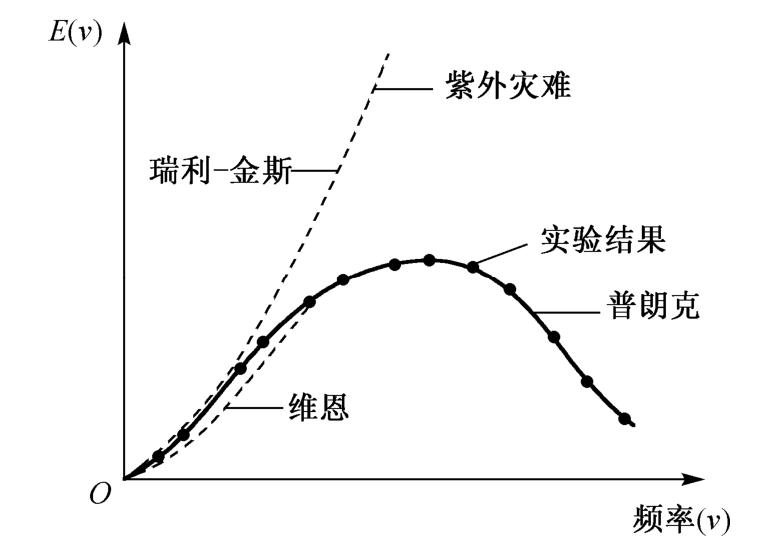
图1.1 黑体辐射的能量密度随频率的变化
1900年,瑞利(Rayleigh)根据经典电动力学和统计物理理论得出一个黑体辐射公式,并由金斯(Jeans)在1905年进行了修正,即瑞利-金斯公式:

该式在低频段时与实验值符合较好,但在高频段时与实验值相差较大。而且由式(1.2)可见,辐射能量密度与频率的平方成正比,当频率较高时,辐射能量趋于无穷大,即向紫外端发散,这完全不符合黑体辐射的真实情况,历史上称为“紫外灾难(Ultra-Violet Catastrophe)”,如图1.1所示。
1900年,普朗克(Planck)在分析维恩、瑞利-金斯公式的基础上,根据黑体辐射能量密度在红外波段(低频区)的精密测量结果,提出了普朗克公式:

c
3
与c
4
是两个参数。普朗克公式在全波段都与观测极为符合。在高频区
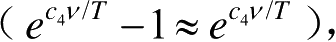 普朗克公式化为维恩公式,在低频区
普朗克公式化为维恩公式,在低频区
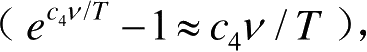 普朗克公式化为
普朗克公式化为

当c 3 /c 4 =8πk/c 3 时,k为玻耳兹曼常数,式(1.4)与瑞利-金斯公式等价。
普朗克发现,如果假定对于一定频率ν的辐射,物体只能以hν为单位吸收或辐射能量(h是一个普适常数,后来人们称之为普朗克常数),则可以从理论上导出它的黑体辐射公式(1.3)。也就是说,物体吸收或发射电磁辐射,只能以“量子”(Quantum)的方式进行,每个“量子”的能量为ε=hν,称为“作用量子”(Quantum of Action)。从经典力学来看,能量不连续的概念是绝对不允许的,所以尽管从这个量子假设可以导出与实验观测极为符合的普朗克公式,在相当长一段时间里普朗克的工作并未引起人们的重视。
爱因斯坦及德拜(Debye)进一步把能量不连续的概念应用于固体中原子的振动,成功地解决了当温度T→0 K时,固体比热趋于零的现象。至此,普朗克提出的能量不连续的概念才逐渐引起物理学家的重视,随后爱因斯坦将能量量子化引入到对光电效应的解释,玻尔将(Bohr)能量量子化引入到对原子结构和氢原子辐射光谱的解释,获得了成功。能量量子化的思想成了量子力学的基石。普朗克由于对基本作用量子的突出贡献,获得1918年诺贝尔物理学奖。
光电效应是指物质(包括金属,以及非金属的固体、液体或气体)中的电子在吸收较短波长的电磁辐射(如可见光或紫外线)的能量后从物质中发射出来的现象。从物质中发射出来的电子称为光电子。
实验发现,对于特定的物质,只有辐射的光大于某一临界频率时才能激发出光电子。该临界频率仅取决于物质组成,而出射的光电子能量取决于光的频率而与光强度无关,这一点无法用光的波动性理论解释。另外,光电效应还有一点与波动说矛盾。按照波动理论,如果入射光较弱,照射的光要经过一段时间的积累才能发射光电子,而实验发现,即使光强很弱,入射光的到达时刻与光电子的产生时间间隔非常短,实验测定值小于10 ns。
光电效应最早是1887年发现的。当时,赫兹(Hertz)发现用紫外线照射电极时更容易产生火花放电,随后,霍尔瓦克(Hallwachs)斯证实这是由于放电间隙出现电荷的缘故。之后,汤姆逊(Thomson)、勒纳德(Lenard)进行了深入的研究,但一直没有合理地解释观察到的现象,直到爱因斯坦给出了正确的解释。1905年,爱因斯坦认为光是由离散能量包(后来叫做光子)组成的,而不是连续波。在此思想的启发下,爱因斯坦得出了光电效应方程,与实验结果很吻合。公式如下:

式中,υ为光电子的速率,ν为入射光的频率,h为普朗克常数,m为光电子的质量,φ为从原子中逸出一个电子所需的能量。在该式中,爱因斯坦扩展了普朗克的黑体辐射理论,认为光量子能量等于频率乘以一个常数(即普朗克常数)。截止频率以上的光子拥有的能量能激发出电子,产生光电效应。采用光量子概念之后,光电效应中出现的疑难随即迎刃而解。由于对光电效应的研究和数学物理理论的卓越贡献,爱因斯坦获得了1921年诺贝尔物理学奖。
通过对光电效应的研究提出的光量子的概念发展了普朗克的能量子假说,对量子理论的发展起重要的作用,同时玻尔也将量子化的思想引入到原子结构中去。
原子的组成和内部结构是19世纪末物理学家关注的重点。1896年,汤姆逊提出如下原子模型:正电荷均匀分布于原子中,电子以某种规则排列镶嵌其中。然而,α粒子(He 2+ 离子)原子散射实验中出现的大角度散射现象对这一模型提出了疑问。基于此,1911年卢瑟福(Rutherford)提出了原子核式结构模型:原子的正电荷都集中在原子的中心,形成原子核,而电子则围绕原子核旋转。此模型可以很好地解释α粒子的大角度散射,但却遇到了如下难题:(1)如果电子围绕原子核做加速旋转运动,则按照经典电动力学,电子将不断产生电磁辐射而动能减小,轨道半径会不断缩小,最后将掉到原子核上去,原子随之塌缩,但是事实表明原子稳定地存在于自然界;(2)电子因电磁辐射而发射的光的频率等于原子中电子的运动频率,应当是连续的光谱,然而从氢气放电管中观察到的氢原子光谱是线状光谱。玻尔创造性地将量子化观点应用到原子中,将普朗克常数h引进卢瑟福模型,提出了三个假设:
(1)原子能够而且只能够稳定地存在于一些稳定的状态,即定态(Stationary State),这些状态分别对应于离散的能量E 1 ,E 2 ,…,可称为能级,原子状态的变化,包括吸收或发射电磁辐射,只能在两个定态之间跃迁(Transition);
(2)原子在两个定态间(对应能级为E 1 和E 2 ,设E 2 >E 1 )跃迁时,发射或吸收的电磁辐射的频率ν为ν=(E 2 -E 1 )/h,如图1.2所示;
(3)电子绕核运动的角动量是量子化的。
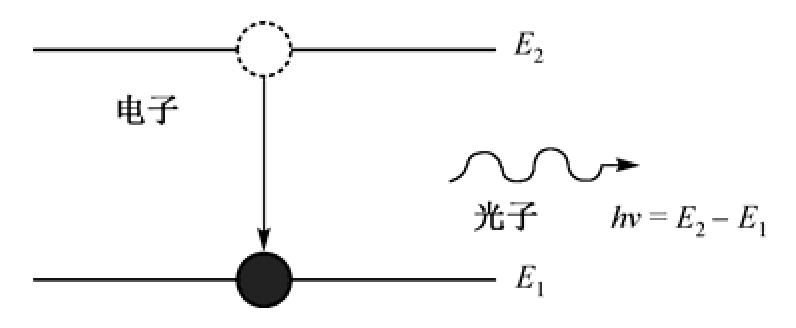
图1.2 原子轨道跃迁示意图
由上述假设(1)可知,原子能够稳定地存在于稳态,除非吸收或发射电磁辐射而改变状态,因而原子可稳定地存在于自然界中;由上述假设(2)可知,电磁辐射的频率与能级之间的能量差有关,因而是离散的;再结合假设(3),可以定量地确定氢原子的能级和光谱频率。可见,玻尔的理论对人们认识原子内部电子运动规律做出了重大贡献。
但是玻尔理论仍存在局限性。玻尔理论虽然成功地说明了氢原子和类氢离子的光谱结构,而且还肯定了氢同位素氘的存在,但是对于更复杂的原子(如氦原子)的光谱,则无能为力;玻尔在描述电子运动时仍采用了轨道的概念,难以解释电子定态能级之间跃迁的物理本质;玻尔理论未能提供处理谱线强度的方法;玻尔理论只能处理周期运动,而不能处理非束缚态问题等。但是,玻尔理论创造性地把量子化的思想用到卢瑟福的原子结构模型中,成功地解释了氢原子光谱之谜,波尔创立的旧量子理论在量子力学的发展上起到了非常重要的作用,为量子理论的发展奠定了基础,他本人也于1922年获得了诺贝尔物理学奖。
光的干涉和光电效应等现象说明了光具有波粒二象性。在普朗克-爱因斯坦的光量子论和玻尔的原子论的启发之下,1923年,德·布罗意(de Broglie)提出微观粒子,如电子、质子或中子,也具有波动性,即实物粒子也具有波粒二象性。他假定具有能量E和动量p的实物粒子,其呈现的物质波(Matter Wave)的频率和波长分别为

实物粒子的波动性在1927年得到实验验证。戴维孙(Davisson)和革末(Germer)将一束电子打在金属镍单晶表面上,观测到了电子衍射的现象,并证实了德· 布罗意关系λ=h/p的正确性。随后,科学家将电子束打在云母薄片上,得到了云母的电子衍射图,打在金箔上得到了同心圆环衍射图样。
后来大量的实验表明质子、中子、原子、分子等都具有波动性。可见,波动性是实物粒子普遍具有的一种性质,波粒二象性成为量子力学基本理论的重要组成部分,物质波的提出者德·布罗意也于1929年荣获了诺贝尔物理学奖。
在德·布罗意提出物质的波动性并得到实验证实后,玻恩(Born)提出用波函数描述微观粒子的状态,指出它是一种概率波。1926年薛定谔(Schrödinger)提出了波函数的波动方程(后来称为薛定谔方程)。薛定谔把原子的离散能级与微分方程在一定的边界条件下的本征值问题联系在一起,成功地说明了氢原子、谐振子等的能级和光谱规律,从而建立起来波动力学。
同年,海森堡(Heisenberg)、玻恩和约当(Jordan)也建立了矩阵力学。在矩阵力学中,每一个物理量(例如粒子的坐标、动量、能量等)都对应一个矩阵(或算符),它们的代数运算规则与经典物理量不同,两个量的乘积一般不满足交换律。量子体系中各力学量(矩阵或算符)之间的关系用矩阵方程或算符方程表述,虽然形式上与经典力学相似,但运算规则不同。矩阵力学成功地解决了谐振子、转子、氢原子等的离散能级、光谱线频率和强度等问题,引起物理学界普遍重视。
同在1926年,薛定谔证明了矩阵力学和波动力学之间是等价的,它们只是用了不同的数学语言来表述而已。虽然当时对量子力学的描述有着多种不同的数学体系,但只有波动力学和矩阵力学获得了广泛的应用。
在科学家对黑体辐射、光电效应、原子的结构和谱线之谜等困惑的探索和研究过程中,能量量子化、光量子理论、物质波等新的思想和理论不断地提出,较好地解答了这些疑惑,量子力学逐渐建立起来了。
量子力学建立后,证明了其在低速、微观的现象范围内具有普遍适用的意义。它是现代物理学基础之一,在现代科学技术中的表面物理、半导体物理、凝聚态物理、粒子物理、低温超导物理、量子化学以及分子生物学等学科的发展中,都有重要的理论意义。量子力学的产生和发展标志着人类认识自然实现了从宏观世界向微观世界的重大飞跃。