




由3.1.3节可知,量子信息的载体如光子、电子和约瑟夫结等都遵循量子力学的基本原理,因而量子信息具有不同于经典信息的特性。在3.2.3节中,我们了解到量子纠缠具有非定域性,在这一节将介绍非正交量子态的不可区分性、未知量子态的不可克隆性和量子测量中的海森堡不确定性原理。
本节我们研究以下问题:如果将信息“0”和“1”编码在两个量子态
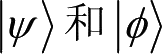 上,通过无噪声信道传输后,接收方能否获知编码的信息呢?设
上,通过无噪声信道传输后,接收方能否获知编码的信息呢?设
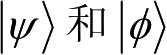 的内积为
的内积为
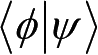 ,若
,若
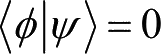 ,则称这两个态正交;若
,则称这两个态正交;若
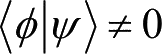 ,则称这两个量子态非正交。则有以下结论:
,则称这两个量子态非正交。则有以下结论:
定理3.2 如果两个量子态是正交的,则可以通过量子测量进行成功概率为1的准确区分;如果两个量子态是非正交的,则无法通过量子测量进行成功概率为1的准确区分。
证明:使用反证法,设存在一组量子测量算子可以概率1准确区分态
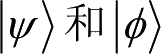 。不失一般性,令此组POVM测量算子具有形式:
。不失一般性,令此组POVM测量算子具有形式:
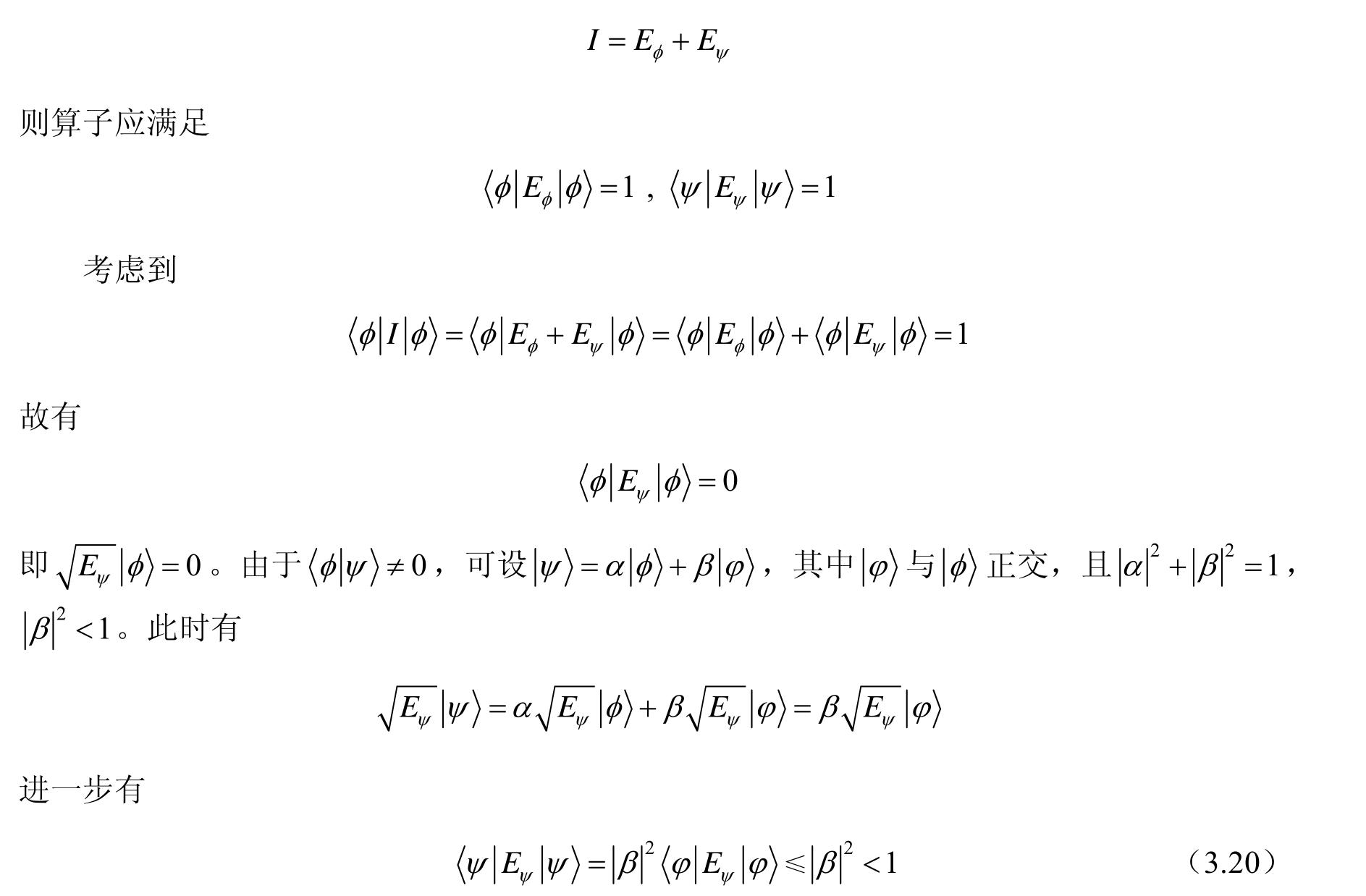
式(3.14)与假设
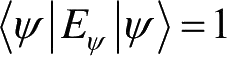 矛盾,故假设不成立,定理得证。
矛盾,故假设不成立,定理得证。
然而,尽管无法以概率1准确区分两个非正交量子态,但是尽可能最优地区分
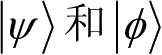 仍然是量子信息中的重要命题。此处有两种折中的手段,第一是牺牲一定的区分成功概率,但要求区分的结果必须准确,称为量子态的无误区分;第二是牺牲一定的准确率,但保证每次区分都给出结果。相关内容可参考文献
[Zeng 2010]
。
仍然是量子信息中的重要命题。此处有两种折中的手段,第一是牺牲一定的区分成功概率,但要求区分的结果必须准确,称为量子态的无误区分;第二是牺牲一定的准确率,但保证每次区分都给出结果。相关内容可参考文献
[Zeng 2010]
。
克隆(Clone)是遗传学上的术语,是指来自同一个祖先、经过无性繁殖所产生相同的分子(DNA、RNA)、细胞的群体或遗传学上相同生物个体。能否克隆出一个与未知量子比特完全相同的新量子比特,而且同时不破坏原来的量子比特?1982年Wootters和Zurek在《Nature》上发表了一篇题为“单量子态不可克隆”的论文,提出了著名的量子不可克隆定理 [Wootters 1982] 。
定理3. 3 未知量子态不可能被克隆。
下面看这个定理的简单证明 [Desurvire 2009] 。
证明:若要完成量子态克隆过程,需要两个量子系统,系统A作为待克隆的量子态输入,初始时可处于任意态
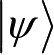 ,另外一个系统B,初始时处于一个标准的纯态
,另外一个系统B,初始时处于一个标准的纯态
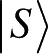 。克隆过程由A和B复合系统上的一个幺正算子U来描述,则克隆任意输入态要求式
。克隆过程由A和B复合系统上的一个幺正算子U来描述,则克隆任意输入态要求式
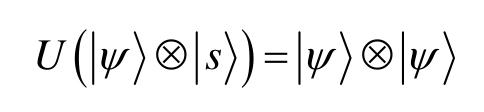
对任意输入态
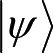 都成立。则对系统A中的另一个态
都成立。则对系统A中的另一个态
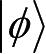 (满足
(满足
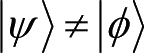 )也可以复制到系统B中,即
)也可以复制到系统B中,即
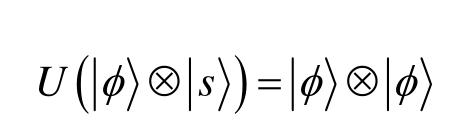
取上面两个方程的内积,并考虑幺正算符U的特性U
+
U=I,对纯态
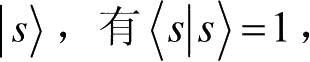 有
有
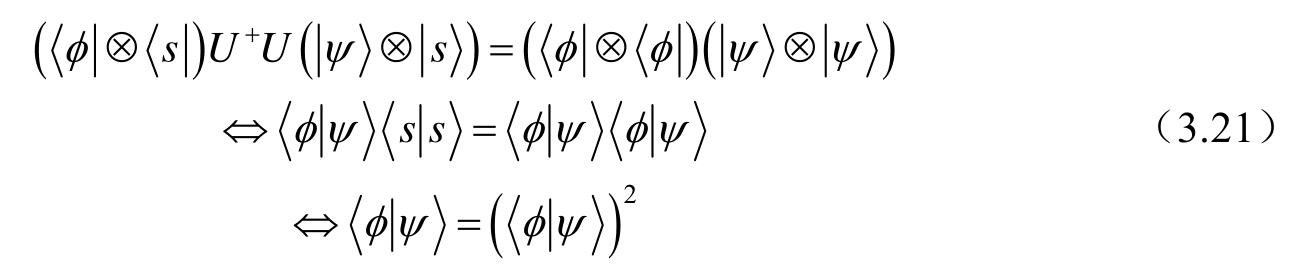
上式有两个可能的解:
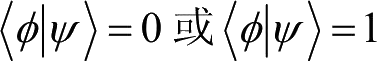 ,即两态相等或者正交。上述结果表明,一部以幺正变换的方式且成功概率为1的量子克隆机只能克隆相互正交的一对量子态。能够以幺正变换的方式且成功概率为1的克隆任意量子态的克隆机是不存在的。
,即两态相等或者正交。上述结果表明,一部以幺正变换的方式且成功概率为1的量子克隆机只能克隆相互正交的一对量子态。能够以幺正变换的方式且成功概率为1的克隆任意量子态的克隆机是不存在的。
海森堡不确定性原理(Heisenberg Uncertainty Principle)由德国物理学家海森堡于1927年提出,突出地表现了量子系统与宏观经典系统的显著不同。对两个力学量C和D,定义其测量的不确定量为


值得特别注意的是,一种常见的误解是将海森堡不确定性原理理解为“在对量子系统先后对力学量C和D测量时,对力学量C的测量将影响对力学量D的测量”。尽管量子测量将改变待测系统所处的量子状态,进而影响后续的测量结果,但这并非海森堡不确定性原理的准确含义。海森堡不确定性原理是指制备大量待测量子态
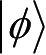 的条件下,对一部分系统测量C,另一部分测量D,则对力学量C和D测量的不确定量的乘积大于等于C与D对易算符期望的绝对值的一半。
的条件下,对一部分系统测量C,另一部分测量D,则对力学量C和D测量的不确定量的乘积大于等于C与D对易算符期望的绝对值的一半。