2.2 纯态与混合态

纯态与混合态是量子力学和量子通信中的重要概念。本节讨论纯态与混合态的定义与描述方式，包括密度矩阵的动力学方程、约化密度矩阵，以及Schmidt分解与混合态的纯化。

2.2.1　 混合态的定义与描述

在量子力学中，如果系统的状态可以用确定的态矢量（或概率幅）来描述，则称此状态为纯态（pure state）。最简单的纯态是力学量的一组完全本征态，当然，纯态也可以是本征态的相干叠加态。如果系统的若干个纯态以一定的概率非相干的混合，则形成的这种状态称为混合态（mixed state）。注意这些纯态不是相干叠加，否则为纯态。

定义 设系统处于混态，在某一时刻，系统按已知概率p _i 处于一些纯态 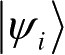，则此系统的状态由密度矩阵ρ描述为

密度矩阵也称为密度算子。若一个量子系统处于纯态 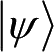，则密度矩阵为

任意可观测力学量Ω在混态系统中的期望值可写为

密度矩阵有如下的性质：

（1）密度矩阵为Hermite的，即ρ＝ρ ^＋ ；

（2）密度矩阵的本征值为非负；

证明：ρ是一个半正定算子：对于状态空间中任意向量，有

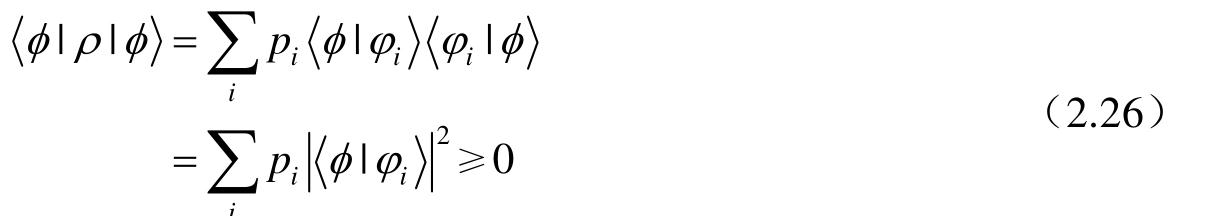
（3）ρ对角元0≤ρ _nn ≤1；

（4）ρ的迹等于1；

证明：

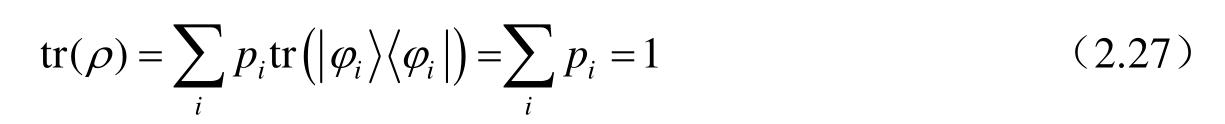
（5）tr(ρ ² )≤1；

当系统处于纯态时，密度矩阵的本征值为1；此时，密度矩阵为投影算符；tr(ρ ² )＝1。

2.2.2　混合态的动力学方程与测量

从薛定谔方程出发，可以推得混合态的动力学演化方程。假设一个量子系统以概率p _i 处于初始状态 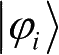，由公设3可以推知系统演化的动力学方程为

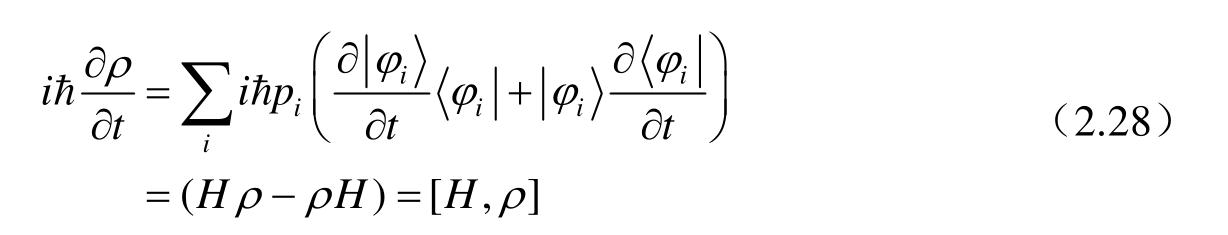
其中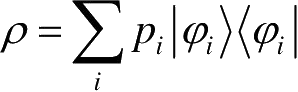， ，H为系统的Hamilton量，记[H,ρ]＝Hρ－ρH，称为算子H和算子ρ的对易子。

系统的演化可以用演化幺正算子U来描述，则系统演化发生以后，系统将以概率p _i 进入状态U 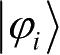。此时，混合态的演化可以描述为

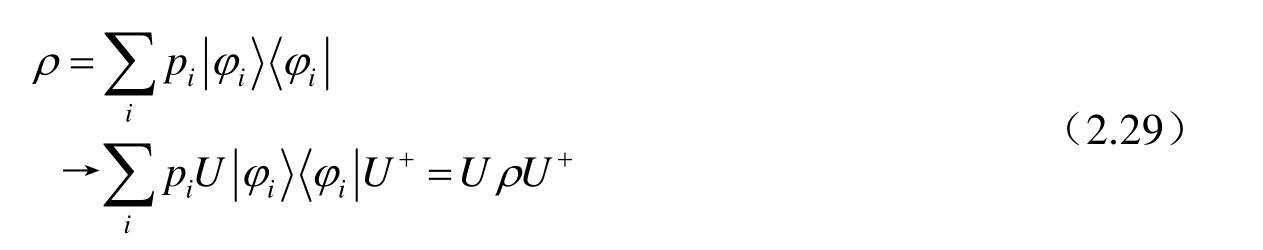
由测量公设出发，可以推出对混合态进行量子测量的数学描述。假设系统初始处于混合态 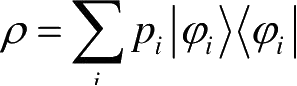，对该量子系统进行由测量算子M _m 描述的量子测量。由于系统以概率p _i 处于初始状态 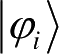，则当测量发生以后，针对 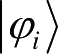得到结果m的概率是

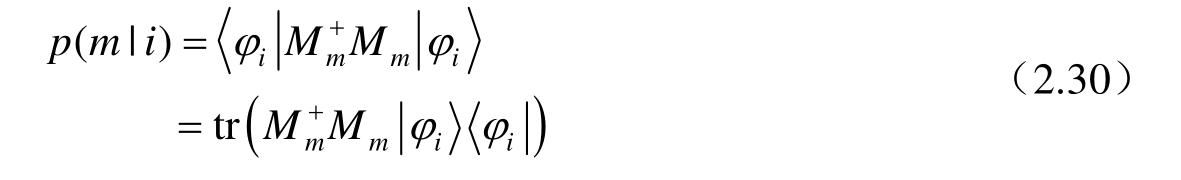
根据全概率公式，对所有可能的态，测量得到结果m的概率是

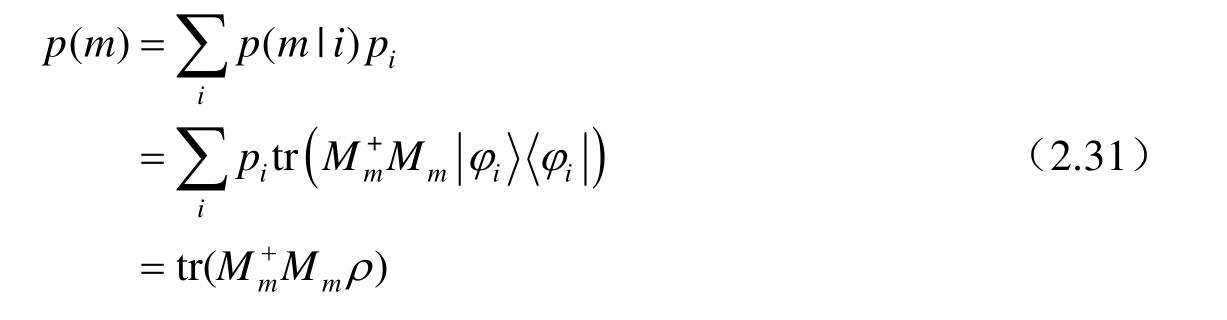
相应的系统末态密度算子为

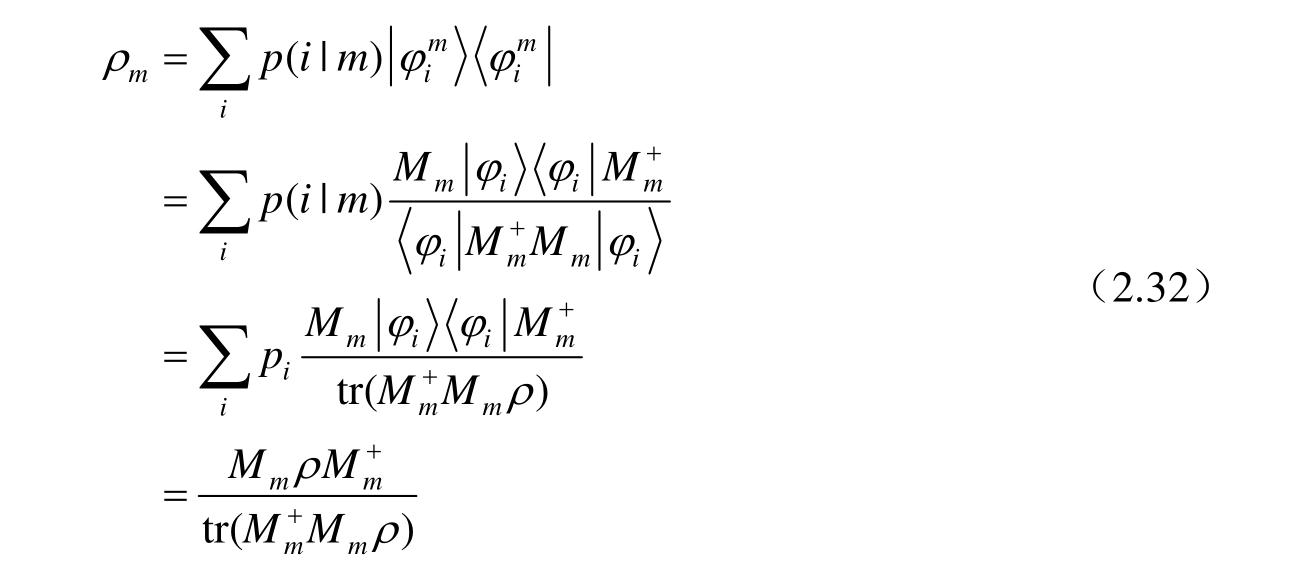
其中，测量算子满足完备性方程

2.2.3　约化密度矩阵

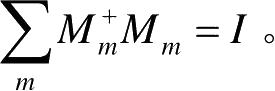
当研究的物理系统不再是一个封闭系统时，系统本身与外界环境不可避免地存在相互作用。在环境与研究者所关心的物理系统相互作用后，为了简化描述，可以采用约化密度矩阵的方式约去系统描述中环境的部分。设物理系统A和物理系统B（环境）组成复合系统，其状态由密度算子ρ _AB 来描述，则系统A的约化密度算子定义为 ^{[Nielsen 2000]}

其中，tr _B 是一个线性算子，称为系统B上的偏迹。当求偏迹的密度矩阵可以写成矩阵直积的形式时，偏迹定义为

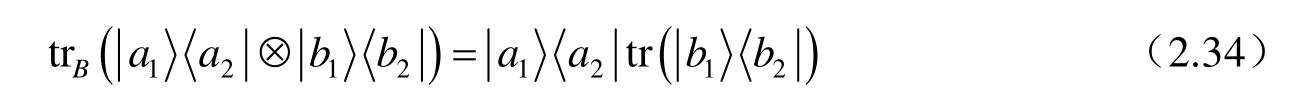
其中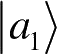， 和 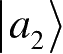是状态空间A中的两个向量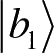， 和 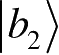是状态空间B中的两个向量。考虑到ρ _AB 总可以写成多个矩阵直积的和以及tr _B 的线性性质，式（2.34）实际上给出了求任意矩阵偏迹的方法，此处给出一个例子。

如果联合系统的状态是一个精确已知的纯态，表示为

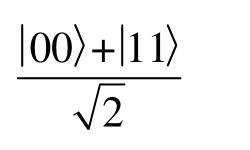
它的密度算子为

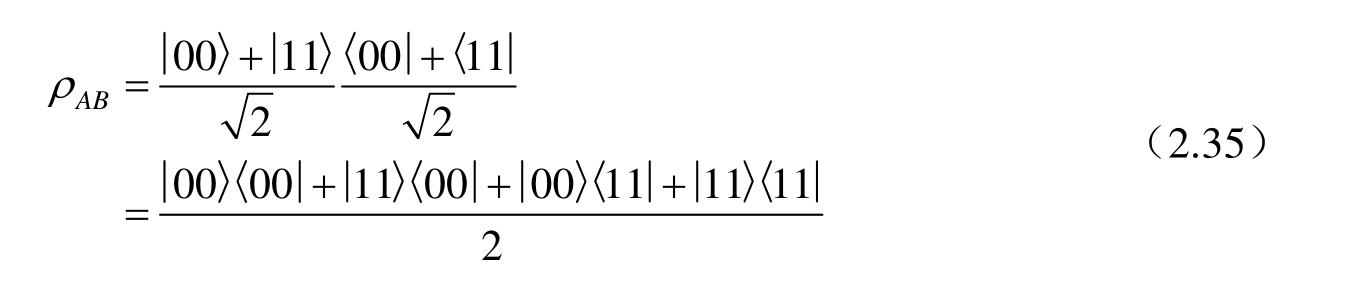
对子系统B求偏迹，可以得到子系统A的约化密度算子

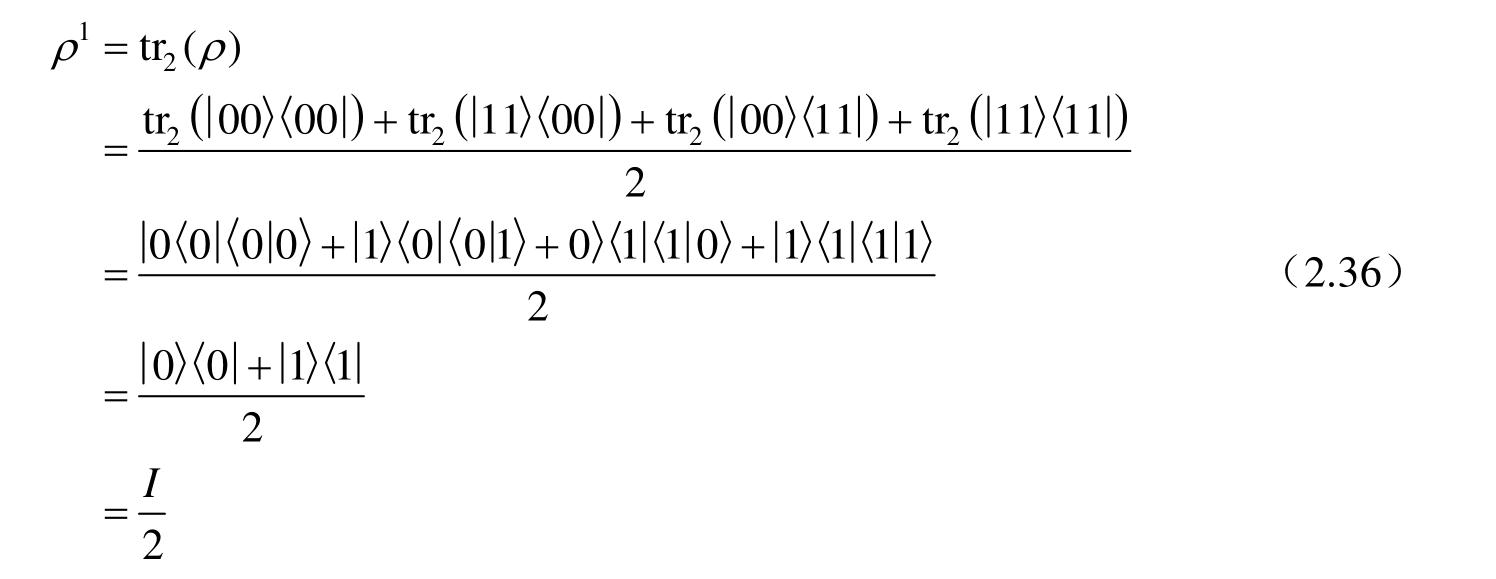
因为 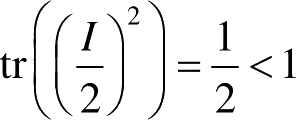，所以子系统A处于混合态，同样的方法可以验证子系统B也处于混合态。这个结果非常值得关注，复合系统的状态是一个精确已知的纯态，但第一个量子比特构成子系统，却处于混合态，其状态无法完全确知。换句话说，一个复合系统的联合状态全已知，但其子系统的状态却不知，这是量子系统区别于经典系统的特点之一。

2.2.4　Schmidt分解与混合态的纯化

研究复合量子系统时，除了密度算子和偏迹外，Schmidt分解和纯化（Purification）也可用来研究复合量子系统。这里，先给出Schmidt分解定理，并进行简要证明 ^{[Nielsen 2000]} 。

定理2.1 （Schmidt分解）设 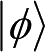是复合系统AB的一个纯态，则存在系统A的标准正交基 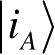和系统B的标准正交基 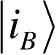，使得

其中，λ _i 是满足 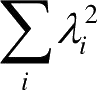＝1的非负实数，称为Schmidt系数。

证明 ：假定系统A和B的状态空间具有相同的维数，设 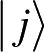和 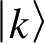分别为系统A和B的标准正交基，则 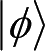对矩阵a（其元素a _jk 为复数）可写成

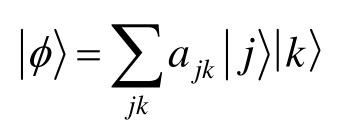
由矩阵的奇异值分解，a＝udυ，其中d是具有非负元素的对角阵，u和υ是幺正矩阵。于是

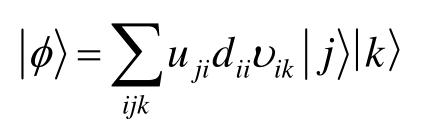
定义 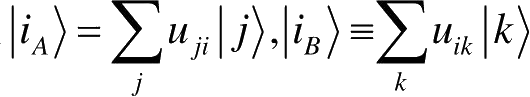和，λ _i ≡d _ii 可给出

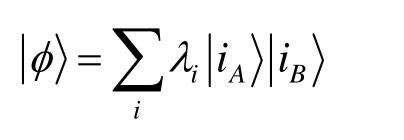
从u的幺正性和 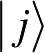的标准正交性，容易验证 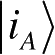构成一个标准正交集，同理 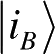也构成一个标准正交集.

基 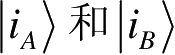分别称为A和B的Schmidt基，且非零λ _i 的个数称为状态 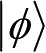的Schmidt数。

Schmidt数是复合量子系统的重要属性，在某种意义下是指量化系统A和B之间纠缠的“量”。Schmidt数在系统A或B的单独幺正变换下保持不变，这种代数不变性使Schmidt数成为非常有用的工具。

Schmidt分解在量子信息中非常有用，下面举例说明。

令 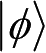是复合系统AB的一个纯态，则由Schmidt分解，可得 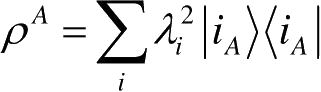和 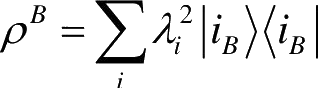，于是两个密度算子ρ ^A 和ρ ^B 的特征值相同，即均为 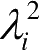。量子系统的许多重要性质完全取决于系统约化密度算子的特征值，因此对复合系统的纯态而言，两个系统的这些性质相同。

Schmidt分解在量子信息中还有许多其他的应用，它可以简化复合系统，便于分析。

与量子信息有关的另一技术是纯化（Purification）。给定量子系统A的状态ρ ^A ，可以引入另一个系统，记做R，并为联合系统AR定义纯态 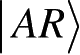，使得 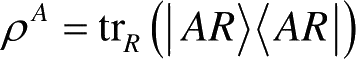。也就是说，当我们只看系统A时，纯态 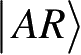退化为ρ ^A 。这是一个纯粹的数学过程，称为纯化，这就把纯态和混合态联系起来了。为此称R为参考系统：它是一个假想的系统，没有直接的物理意义。

为证明纯化可以对任意状态进行，我们来说明如何为ρ ^A 构造系统R和纯化 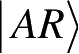。设ρ ^A 有标准正交分解 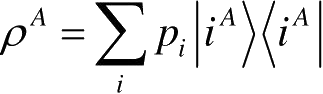，为对ρ ^A 进行纯化而引入系统R，它与A具有相同的状态空间，有标准正交基 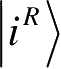。为复合系统定义纯态：

现在计算系统A对应于状态 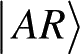的约化密度算子：

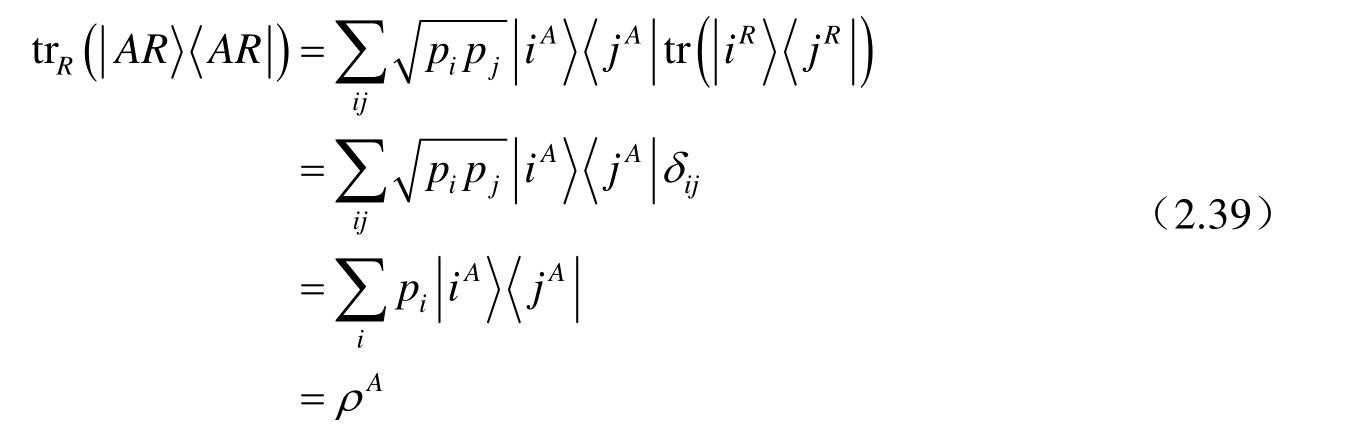
可见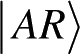， 是ρ ^A 的纯化。

注意Schmidt分解和纯化有密切的关系：用于纯化一个系统A混合态的过程是定义一个纯态。该纯态相对系统A的Schmidt基恰好将系统A混合态对角化，并且Schmidt系数是被纯化的密度算子的特征值的平方根。 HbIcoVXerUTunP5SEJyihX3gvWsYS3bBxujyBEaBlsajxdH5OhCAtkvBS2mXePsI