




本节将给出量子力学的5个公设,涵盖量子力学涉及的部分重要的基础理论,具体为:公设1说明量子力学如何描述物理系统;公设2说明量子力学如何刻画物理量;公设3给出封闭量子力学系统演化的动力学方程;公设4给出获取量子系统信息的测量理论;公设5描述如何描述复合量子系统。
公设1:任一孤立的物理系统中,都存在一个被称为系统状态空间的复内积向量空间(Hilbert空间)与之联系,系统状态完全由状态空间向量所描述,并且向量是系统状态空间的一个单位向量 [苏汝铿 2002] 。
在经典力学中,微观粒子在某一确定的时刻必然具有确定的位置。然而,在量子力学中,微观粒子在确定的时刻,一般没有确定的位置,而是以一定概率在每个可能的位置出现。量子力学理论认为,微观粒子的状态可以由波函数完全描述。
波恩(Born)指出:某一时刻,波函数在空间中某一点的强度(即其振幅模的平方)和在这一点中找到粒子的概率成正比,和粒子相联系的波是一种概率波。令波函数为
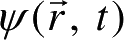 ,则
,则
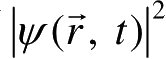 表示在t时刻粒子出现在
表示在t时刻粒子出现在
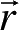 处的概率。由于某时刻粒子在空间中某点出现的概率是单值,因此在一般情况下,除个别孤立点外,波函数
处的概率。由于某时刻粒子在空间中某点出现的概率是单值,因此在一般情况下,除个别孤立点外,波函数
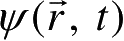 应该是
应该是
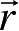 的单值、有界和连续函数。对于许多物理状态,粒子在全空间出现的概率为1,因此一般要求波函数
的单值、有界和连续函数。对于许多物理状态,粒子在全空间出现的概率为1,因此一般要求波函数
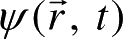 应是平方可积函数,且满足归一化条件,即
应是平方可积函数,且满足归一化条件,即

基于上述波函数的描述,如果
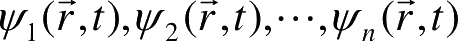 是体系的可能状态,则它们的线性叠加所得出的波函数
是体系的可能状态,则它们的线性叠加所得出的波函数
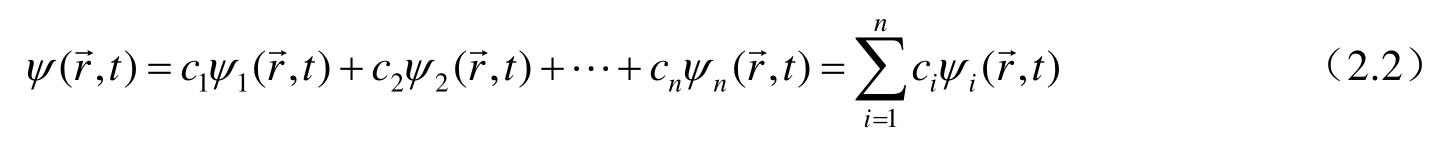
也是体系的一个可能状态,这称为量子力学的态叠加原理。在这里,并不要求各个波函数之间是正交的,但总可以通过Hilbert空间的正交化方法,把
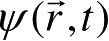 写成一组正交波函数的叠加。
写成一组正交波函数的叠加。
为了方便地表示系统的状态,狄拉克引入了符号
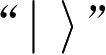 (右矢,ket)表示系统的状态,其转置共轭标示为“
(右矢,ket)表示系统的状态,其转置共轭标示为“
 ”(左矢,bra)。
”(左矢,bra)。
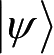 就可以表示系统的一个量子态,可以认为其等价于
就可以表示系统的一个量子态,可以认为其等价于
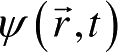 ,再比如
,再比如
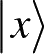 就可表示粒子处于位置x的量子态。本书中将更多地采用狄拉克符号表示法来表示系统的量子态,在无限维的Hilbert空间中,
就可表示粒子处于位置x的量子态。本书中将更多地采用狄拉克符号表示法来表示系统的量子态,在无限维的Hilbert空间中,
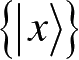 可以构成一组正交归一基函数。如果某粒子处于态ψ(x)(为方便起见,考虑一维空间,并且省去时间参数t),那么该粒子的的状态用狄拉克符号
可以构成一组正交归一基函数。如果某粒子处于态ψ(x)(为方便起见,考虑一维空间,并且省去时间参数t),那么该粒子的的状态用狄拉克符号
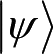 表示,可写为
表示,可写为

其中,
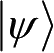 为粒子的状态,ψ(x)为粒子处于位置x处的概率幅,也就是波函数,
为粒子的状态,ψ(x)为粒子处于位置x处的概率幅,也就是波函数,
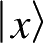 为基函数。由此可以看出,波函数和狄拉克符号都可以用来表述系统的量子态,两者一一对应。由于系统状态空间的“正交归一基态”
为基函数。由此可以看出,波函数和狄拉克符号都可以用来表述系统的量子态,两者一一对应。由于系统状态空间的“正交归一基态”
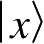 (基函数对应的状态)满足
(基函数对应的状态)满足
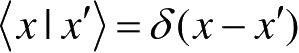 ,则
,则
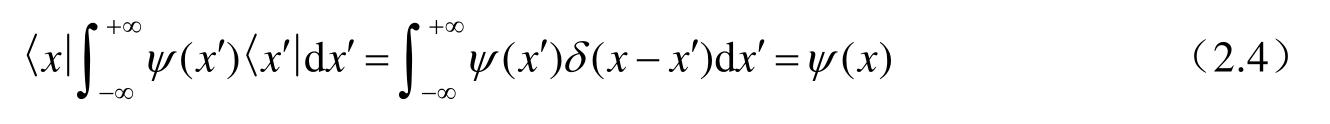
即,
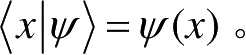
由公设1,系统的状态
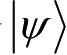 对应于Hilbert空间的单位向量,称
对应于Hilbert空间的单位向量,称
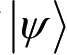 为态矢。式(2.3)即表示态矢按本征值展开,当本征矢为有限个时,式(2.3)可表达为
为态矢。式(2.3)即表示态矢按本征值展开,当本征矢为有限个时,式(2.3)可表达为

其中,
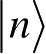 为本征矢,
为本征矢,
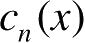 为对应系数,
为对应系数,
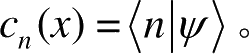
公设2:(力学量)量子力学中,任意实验上可以观测的力学量均由一个线性厄米算子F描述,其厄米性要求

F
†
表示F的转置共轭。线性厄米算子有两个重要性质:第一,线性厄米算子的本征值必为实数,其所有本征矢是完备的,且属于不同本征值的本征矢彼此正交;第二,任何量子态
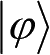 下,线性厄米算子的平均值
下,线性厄米算子的平均值
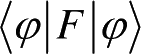 必为实数。
必为实数。
由公设1可知,若给出微观粒子的波函数,就确定了微观粒子的运动状态。此状态下系统的力学量,如坐标、动量、角动量、能量等,一般并不具有确定的数值,只具有一系列可能值,每一可能值均以一定的概率出现。当给定描述这一运动状态的波函数后,力学量出现各种可能值的相应的概率就被完全确定。
设定义在n维Hilbert空间中的力学量F具有n个本征值f
i
(非简并的情况),分别对应本征矢
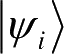 ,其中(i=1,…,n)。由
,其中(i=1,…,n)。由
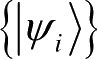 的完备性可知,系统所处的任意量子态
的完备性可知,系统所处的任意量子态
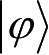 均可展开为
均可展开为
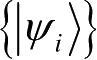 中元素的线性叠加
中元素的线性叠加

式中,
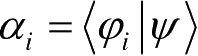 。当对力学量F进行测量时,每次测量的结果只能得到F的本征值之一,得到此结果的概率对应上式中的展开系数的模方
。当对力学量F进行测量时,每次测量的结果只能得到F的本征值之一,得到此结果的概率对应上式中的展开系数的模方
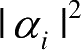 。
。
在量子通信中,经常会用到一组力学量算符
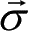 ,也称为Pauli算符,这里给出其各分量的定义:
,也称为Pauli算符,这里给出其各分量的定义:
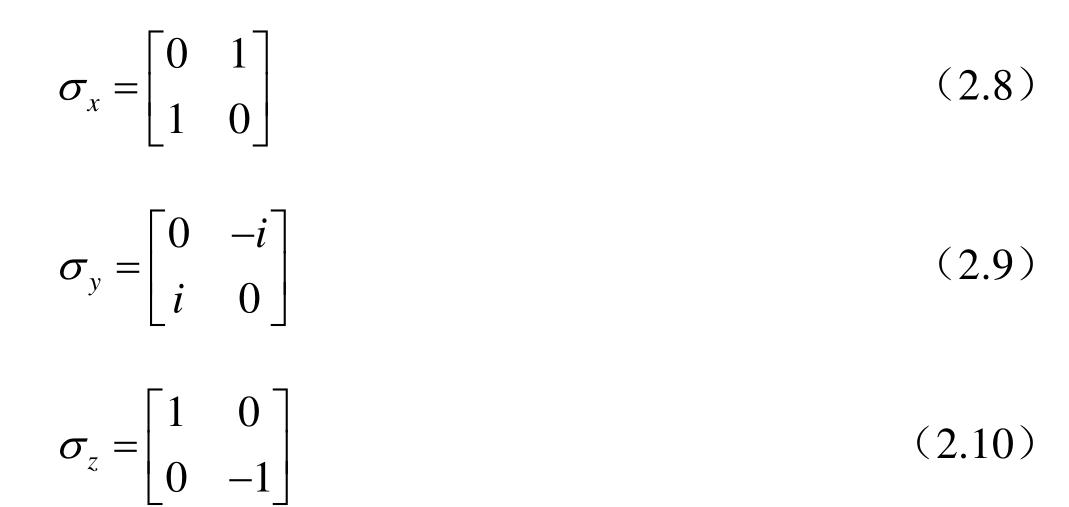
Pauli算符在不同的物理背景下代表的力学量有所不同,本书将在具体上下文中指明。
公设3:封闭量子系统的演化由Schrödinger方程描述

该方程中,ħ称为Planck常数;H是一个厄米算子,称为封闭系统的Hamilton量。由式(2.14)可见,系统的演化状态可以通过求解微分方程得出,而获得特定物理系统的Hamilton量的具体形式需要通过大量的实验确定,这一直是物理学研究的重要问题,而且对于一些常用的量子系统已经得到了很多明确的结论。在量子信息学中,一般不讨论如何确定Hamilton,只是简单假设所讨论量子系统的Hamilton为已知。
首先,Hamilton量可以用于确定系统可能处于的状态。由上所述,Hamilton量是一个Hermite算子,所以有谱分解

其中,λ
i
习惯上称做能量特征值;
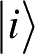 为对应的特征向量,习惯上称做能量本征态。对于氢原子Hamilton量来说,谱分解所得到的本征态联系着氢原子的一条谱线。
为对应的特征向量,习惯上称做能量本征态。对于氢原子Hamilton量来说,谱分解所得到的本征态联系着氢原子的一条谱线。
另一方面,若给定系统的Hamilton量和t 0 时刻的初态,由方程初值问题解的唯一性可知,系统t(t 0 <t)时刻的态是唯一确定的。采用狄拉克的表示方法,这个态演化的过程可以用一个算子U来描述,即有

式中,算子U(t 0 ,t)将系统t 0 时刻的态矢量变为t时刻的态矢量,称为演化算子。显然,演化算子的形式应由薛定谔方程中的Hamilton量所决定。特别地,当Hamilton量不含时间变量时,由薛定谔方程可导出演化算子的具体形式

公设4:一个一般的量子测量由一族线性算子{M m }来描述。这些算子作用在要测量系统的状态空间上,且满足完备性条件

其中,指标m表示测量可能产生的结果。假设测量前系统处于状态
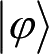 ,则观测到结果m的概率为
,则观测到结果m的概率为

测量后系统的状态为

公设4给出了量子测量的最一般形式,由这样一组线性算子{M m }来描述的测量一般称为量子广义测量,或量子一般测量 [Nielsen 2000] 。
量子广义测量是量子测量的最一般形式,其基本数学描述由公设4给出,其中包含两个要素:
(1)测量结果的概率特性。量子测量得到不同结果的概率由等式p(m)给出,完备性条件保证了所有结果的概率和为1。
(2)测量之后系统的态。系统测量后的态取决于测量结果,对应不同测量结果的末态形式由式(2.17)给出。
量子投影测量是量子广义测量的一个重要特例。当公设4中的测量算子{M m }除满足完备性条件等式外,还满足{M m }是正交投影算子的条件,即

则量子广义测量退化为投影测量{P m }。
量子投影测量的重要意义在于以下两个方面。第一,从抽象的数学描述来说,投影测量是量子测量中最简单的模型,例如,量子信息学中经常引用的在“某一组正交归一基
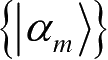 上的测量”即是指投影测量{P
m
},其中
上的测量”即是指投影测量{P
m
},其中

第二,从物理的角度看,对任何可观测的力学量所做的测量本质上都是投影测量。由公设3,任何可观测的力学量都可由一个线性厄米算子描述。设某一力学量对应线性厄米算子Q,
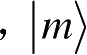 是Q属于特征值m的本征矢,则
是Q属于特征值m的本征矢,则
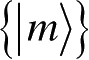 构成了原空间的一组正交归一基。对力学量Q的测量即为在正交归一基
构成了原空间的一组正交归一基。对力学量Q的测量即为在正交归一基
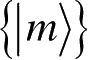 上进行的投影测量,其测量算子相应地记为
上进行的投影测量,其测量算子相应地记为
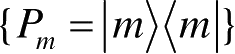 。设系统测量前处于状态
。设系统测量前处于状态
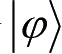 ,则对应特征值m的测量结果产生的概率为
,则对应特征值m的测量结果产生的概率为

这与公设3中给出的结果一致,又由公设4可知,测量后系统的状态将塌缩到态
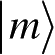 。
。
正算子测量(Positive-Valued Operator Measurement,PVOM)是量子广义测量的数学简化形式。在实际的信息处理中,许多情况下往往只对测量的结果感兴趣,而对测量后系统状态并不关心。设量子一般测量算子{M
m
}在状态为
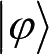 的量子系统上进行测量,此时可以重新定义
的量子系统上进行测量,此时可以重新定义

根据公设3和代数知识可知,E
m
是满足∑
m
E
m
=1和p(m)=
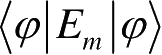 ≥0的半正定算子。E
m
称为一个PVOM元,完整的集合{E
m
}称为一个PVOM测量。需要注意的是,PVOM应被视为研究量子一般测量的统计特性时的一种方便的数学工具,而非一种特定的测量模式。从这个意义上来说,物理上实现一个量子一般测量和实现其对应的PVOM测量是等价的。
≥0的半正定算子。E
m
称为一个PVOM元,完整的集合{E
m
}称为一个PVOM测量。需要注意的是,PVOM应被视为研究量子一般测量的统计特性时的一种方便的数学工具,而非一种特定的测量模式。从这个意义上来说,物理上实现一个量子一般测量和实现其对应的PVOM测量是等价的。
公设5:复合物理系统的状态空间是分物理系统状态空间的张量积,若将分系统编号为1到n,系统i的状态被置为
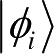 ,则整个系统的总状态为
,则整个系统的总状态为
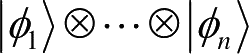 。
。
该公设描述了如何从分系统的状态空间构造出复合系统的状态空间。量子力学的态叠加原理说明,如果
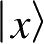 和
和
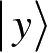 是量子系统的两个状态,那么它们的任意叠加α
是量子系统的两个状态,那么它们的任意叠加α
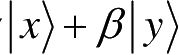 也是量子系统一个可能的状态,其中
也是量子系统一个可能的状态,其中
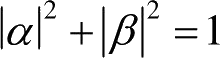 。对于复合系统,如果
。对于复合系统,如果
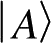 是系统A的一个状态,
是系统A的一个状态,
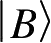 是系统B的一个状态,则联合系统AB的状态可以写为
是系统B的一个状态,则联合系统AB的状态可以写为
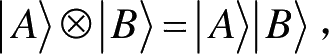 即A与B的张量积。
即A与B的张量积。