





在中段,弹头、诱饵及其他导弹衍生物在径向相对雷达的小幅(相对于目标与雷达的径向距离)非匀速运动或运动分量统称为微动 [8-17] 。微动可分为进动、章动、翻滚或摆动。在中段弹头等目标围绕旋转轴会以一定章动角进行旋转,如果章动角不随时间变化,则这种运动就被称为进动;若章动角随时间周期变化,则这种运动被称为章动 [8-17] 。简而言之,进动是两种单一运动的合成,即“自旋+锥旋”。若把章动角的变化看成是一种“波动”,那么章动就是三种单一运动的合成,即“自旋+锥旋+波动”。摆动为目标围绕摆动轴以固定角度进行的振动。
为了保持弹头在大气层外飞行的稳定性和提高命中精度,弹头在中段要进行姿态控制。虽然诱饵、碎片、末级弹体等衍生物的静态特性与真目标一致,但诱饵、碎片、末级弹体等衍生物一般没有姿态控制。弹头的微动特性与诱饵、碎片、末级弹体等衍生物的微动特性存在显著的差异。
弹道导弹目标可简化为一个锥体目标,锥体弹头的微动模型 [15,17] 如图2.9 所示。由图2.9可见,该目标在本地坐标系(x,y,z)中沿Oz放置(Oz是其对称轴),坐标原点O为其质心。若将其视为弹头,设弹头绕其自身的对称轴Oz自旋,同时绕某一矢量方向O′C旋转,这一旋转周期称为进动周期。O′为Oz与O′C的交点,Oz与O′C之间的夹角称为章动角。
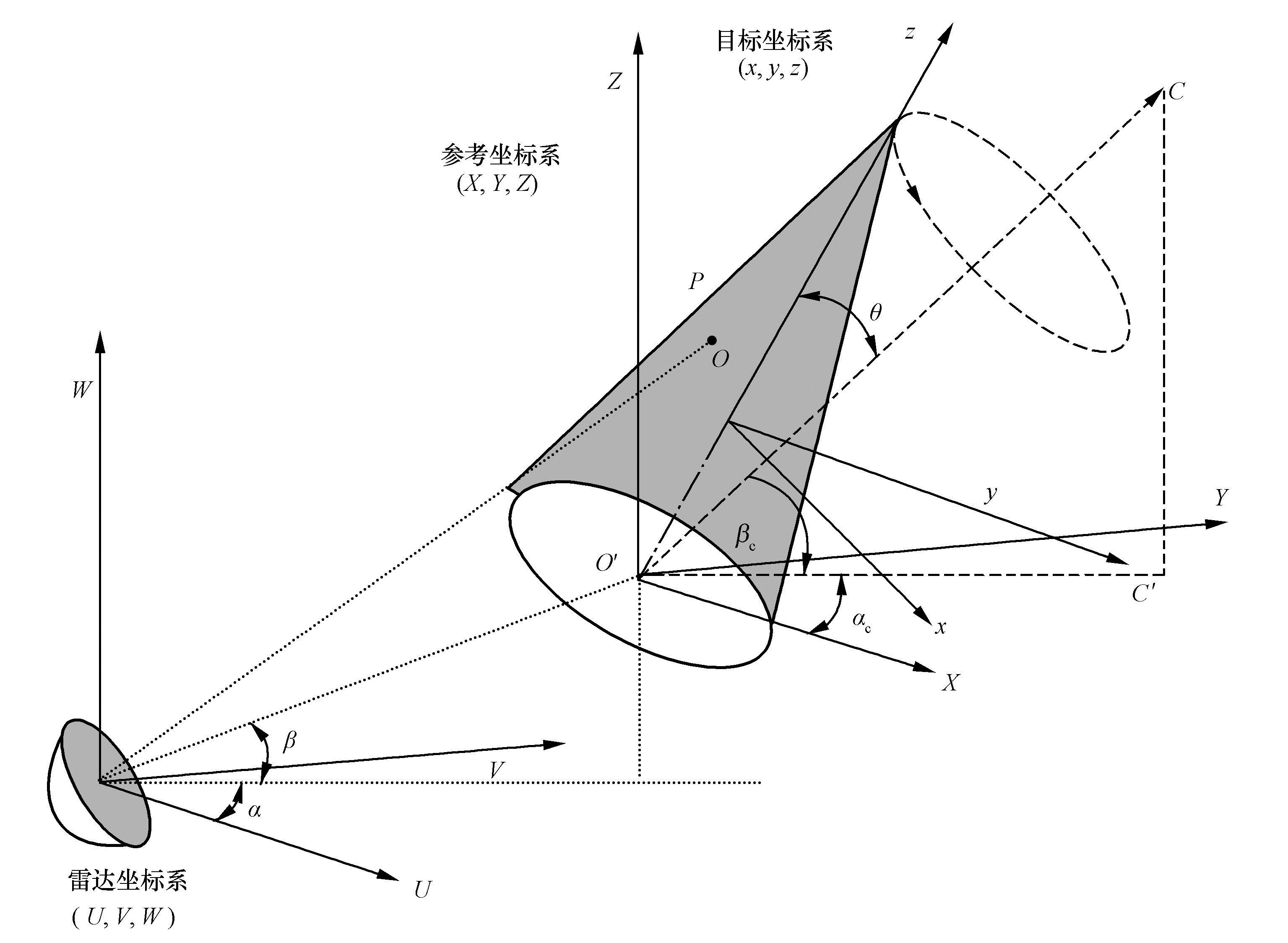
图2.9 弹头微动模型
设坐标原点O′在雷达坐标系中的坐标矢量为R 0 =(U 0 ,V 0 ,W 0 ),在本地坐标系中的位置为r c =(0,0,z 0 ) T 。P为锥体目标上任一散射点,P点在本地坐标系中的初始位置为r P =(x P ,y P ,z P ) T ,在参考坐标系中的初始位置为r 0 =R init (r P -r c ),则 P点在参考坐标系中t时刻的位置P′可以表示为:
r t =(X P ,X P ,X P ) T =T p r 0
(2.5)
式中,R init 为初始旋转矩阵;T p =T p (t)为t时刻的进动矩阵。
设锥体导弹目标的速度为V,则P′点在雷达坐标系中的瞬时位置R t 可以表示为:
R t =R 0 +Vt+r t
(2.6)
下面求进动矩阵T p 。进动是由自旋再锥旋形成的,即它是由自旋和锥旋分别作用而形成的,故t时刻的进动矩阵T p 可表示为:
T p (t)=R c (t)R s (t)
(2.7)
式中,R c (t)为t时刻的锥旋旋转矩阵,R s (t)为t时刻的自旋旋转矩阵。根据 Euler - Rodrigues 绕矢量旋转公式,可得
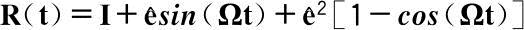
(2.8)
式中,I为3×3单位矩阵;Ω为旋转的角速度;
 为反对称矩阵;若旋转所绕单位矢量为
为反对称矩阵;若旋转所绕单位矢量为
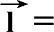 (l
x
,l
y
,l
z
),则
(l
x
,l
y
,l
z
),则
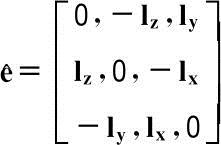
(2.9)
设锥旋的角速度为Ω c ,O′C的单位方向矢量为l c =(A,B,C),则
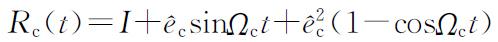
(2.10)
同理,设绕Oz自旋的角速度为Ω
s
,Oz在参考坐标系中的单位方向矢量为
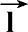 s
=(a,b,c),则
s
=(a,b,c),则
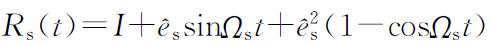
(2.11)
其中,
 c
和
c
和
 s
可以根据
s
可以根据
 得到。
得到。
诱饵等衍生物一般没有姿态控制,在自由段会发生摆动。简化为锥体目标后,诱饵微动模型 [15] 如图2.10所示。
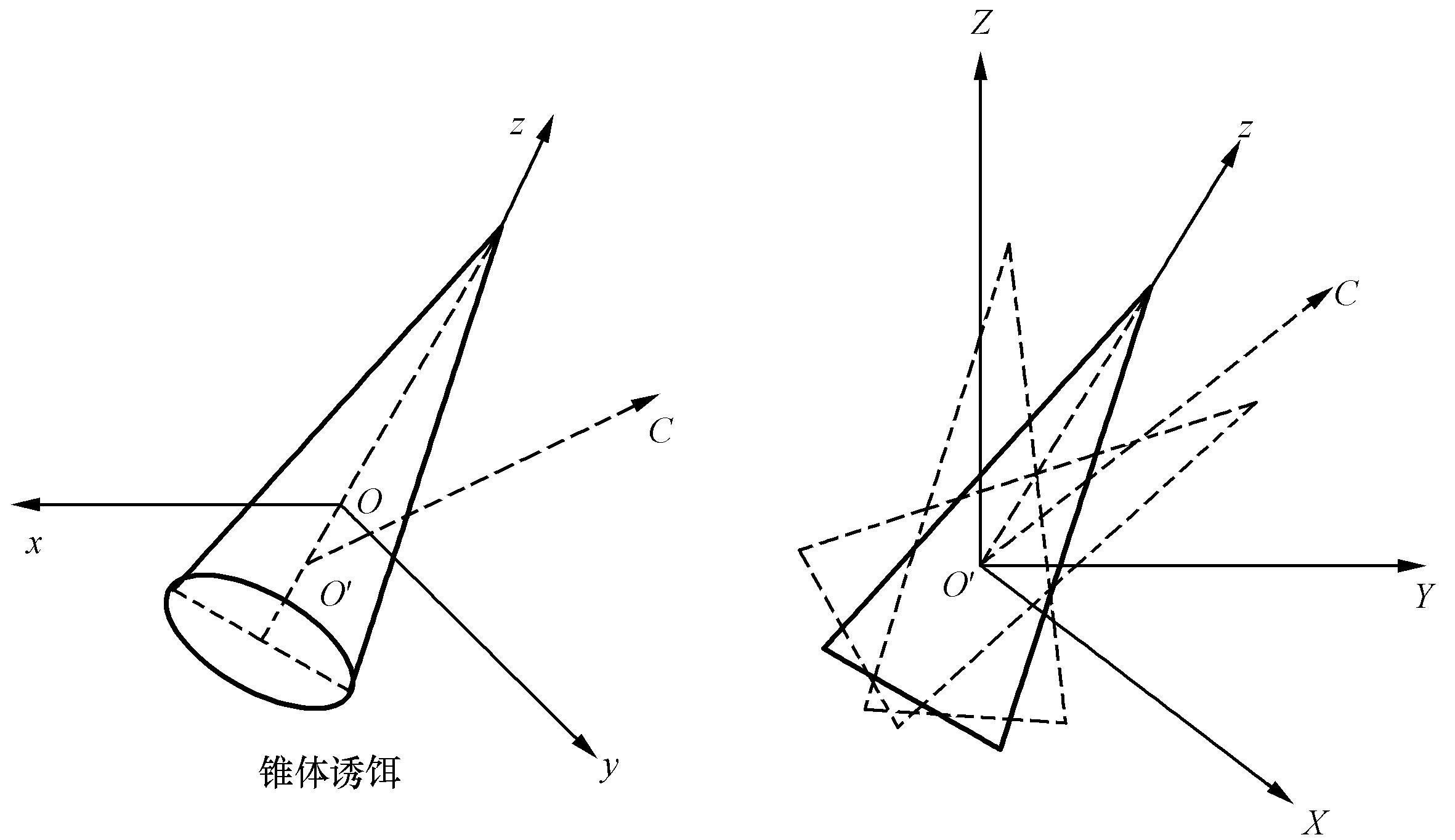
图2.10 诱饵微动模型
诱饵在本地坐标系(x,y,z)中沿Oz放置(Oz是其对称轴),坐标原点O为弹头的质心。给定方向矢量
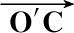 ,
,
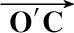 与锥体诱饵对称轴
与锥体诱饵对称轴
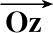 的交点为O′,参考坐标系(X,Y,Z)以O′为坐标原点,且与雷达坐标系(U,V,W)平行。诱饵以O′为中心在
的交点为O′,参考坐标系(X,Y,Z)以O′为坐标原点,且与雷达坐标系(U,V,W)平行。诱饵以O′为中心在
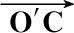 与
与
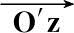 所确定的平面zO′C内摆动。
所确定的平面zO′C内摆动。
设坐标原点O′在雷达坐标系的坐标矢量
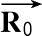 =(U
0
,V
0
,W
0
)
T
,在本地坐标系中的位置为
=(U
0
,V
0
,W
0
)
T
,在本地坐标系中的位置为
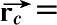 (0,0,z
0
)
T
。P为诱饵上任一散射点,P点在本地坐标系中的初始位置矢量
(0,0,z
0
)
T
。P为诱饵上任一散射点,P点在本地坐标系中的初始位置矢量
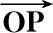 =
=
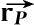 =(x
P0
,y
P0
,z
P0
)
T
,在参考坐标系中
=(x
P0
,y
P0
,z
P0
)
T
,在参考坐标系中
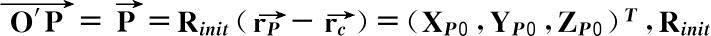 为表征诱饵初始姿态的
Euler
旋转矩阵,P点在参考坐标系中时刻摆动θ角后的位置矢量
为表征诱饵初始姿态的
Euler
旋转矩阵,P点在参考坐标系中时刻摆动θ角后的位置矢量
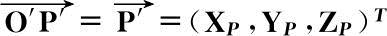 。设
。设
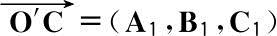 和
和
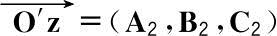 都是参考坐标系下(X,Y,Z)的单位矢量。
都是参考坐标系下(X,Y,Z)的单位矢量。
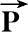 到
到
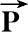 ′的变换可以用一个矩阵来表示,即
′的变换可以用一个矩阵来表示,即
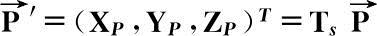
(2.12)
式中,T
s
是一个3×3的变换矩阵。设诱饵的对称轴在本地坐标系中的初始单位方向矢量为
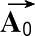 =(0,0,1)
T
,则诱饵的对称轴在参考坐标系中的初始单位方向矢量为
=(0,0,1)
T
,则诱饵的对称轴在参考坐标系中的初始单位方向矢量为
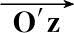 =R
init
(
=R
init
(
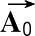 -
-
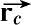 )。令
)。令
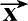 ′=
′=
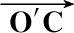 是单位方向矢量
是单位方向矢量
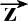 ′=
′=
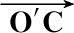 ·
·
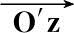 ,
,
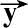 ′=
′=
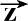 ′·
′·
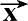 ′,则
′,则
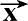 ′、
′、
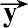 ′和
′和
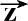 ′互相垂直,交于O′点,且满足右手法则。将
′互相垂直,交于O′点,且满足右手法则。将
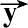 ′和
′和
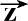 ′分别归一化,则
′分别归一化,则
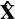 =
=
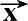 ′,
′,
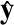 =
=
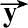 ′/‖
′/‖
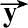 ′‖,
′‖,
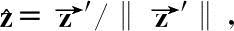 则
则
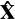 、
、
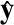 和
和
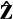 构成一个新的正交坐标系(x′,y′,z′),如图2.11所示。
构成一个新的正交坐标系(x′,y′,z′),如图2.11所示。
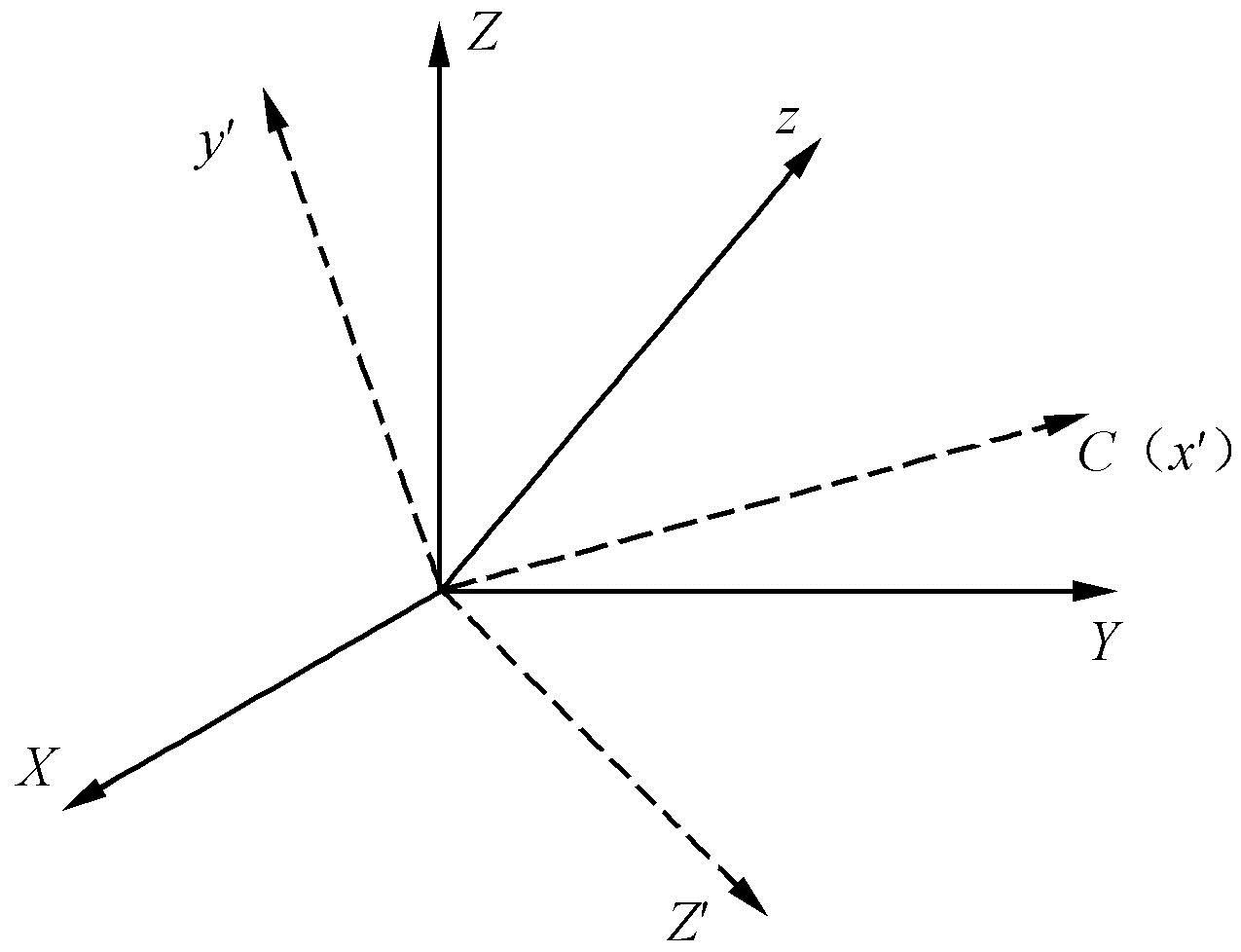
图2.11 复制诱饵摆动运动模型坐标系示意图
设参考坐标系(X,Y,Z)的三个单位方向矢量为
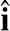 、
、
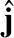 和
和
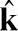 ,则有
,则有
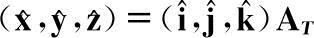
(2.13)
即A
T
为R
3
空间中两组基(
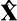 ,
,
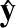 ,
,
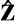 )和(
)和(
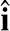 ,
,
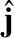 ,
,
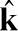 )之间的过渡矩阵,且A
T
为正交矩阵。又因为(X,Y,Z)为自然坐标系,即
)之间的过渡矩阵,且A
T
为正交矩阵。又因为(X,Y,Z)为自然坐标系,即
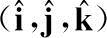 为单位阵,故
为单位阵,故
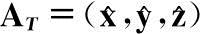
(2.14)
设P点在新坐标系(x′,y′,z′)中的坐标为
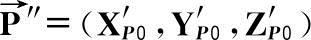 ,则根据基坐标变换公式可得
,则根据基坐标变换公式可得
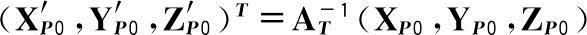
(2.15)
将矢量
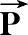 ″绕z′轴旋转角度θ,则得在新坐标系中的坐标为
″绕z′轴旋转角度θ,则得在新坐标系中的坐标为
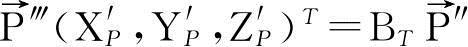
(2.16)
式中,B
T
=
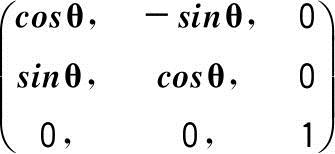 为绕z′转θ角的旋转矩阵,则点P′在坐标系(X,Y,Z)的坐标为:
为绕z′转θ角的旋转矩阵,则点P′在坐标系(X,Y,Z)的坐标为:
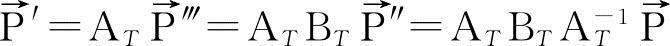
(2.17)
从而
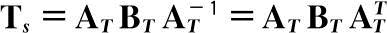
(2.18)
目标微动对电磁波的调制效应称为信号微多普勒调制,导致多普勒频移是时变的,表现在频谱上存在频谱展宽。微动引起的瞬时微多普勒效应可以通过时频像( Time - fre-quency Profile )描述。时频像从瞬时频率上描述了目标微动特征,表征一定观测时间内多散射目标各部件微动速度的分布。
当弹头在中段微动时,回波信号除去载频后的瞬时相位可以表示为:
φ
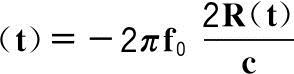
(2.19)
式中,f 0 为发射信号的载频;R(t)为雷达与目标之间的距离。目标的多普勒为:
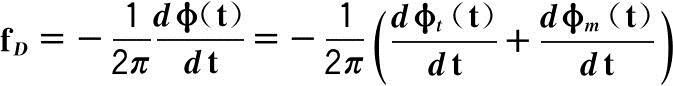
(2.20)
式中,φ t (t)为匀速运动对应的相位;φ m (t)为微动对应的相位。微动产生的多普勒频率为:
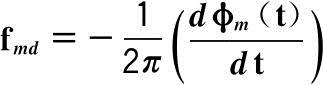
(2.21)
锥体摆动和进动微多普勒理论值和采用SPWD所获得的微多普勒测量结果如图2.12所示,其中锥体锥旋频率为2Hz,摆动频率为2.5Hz。
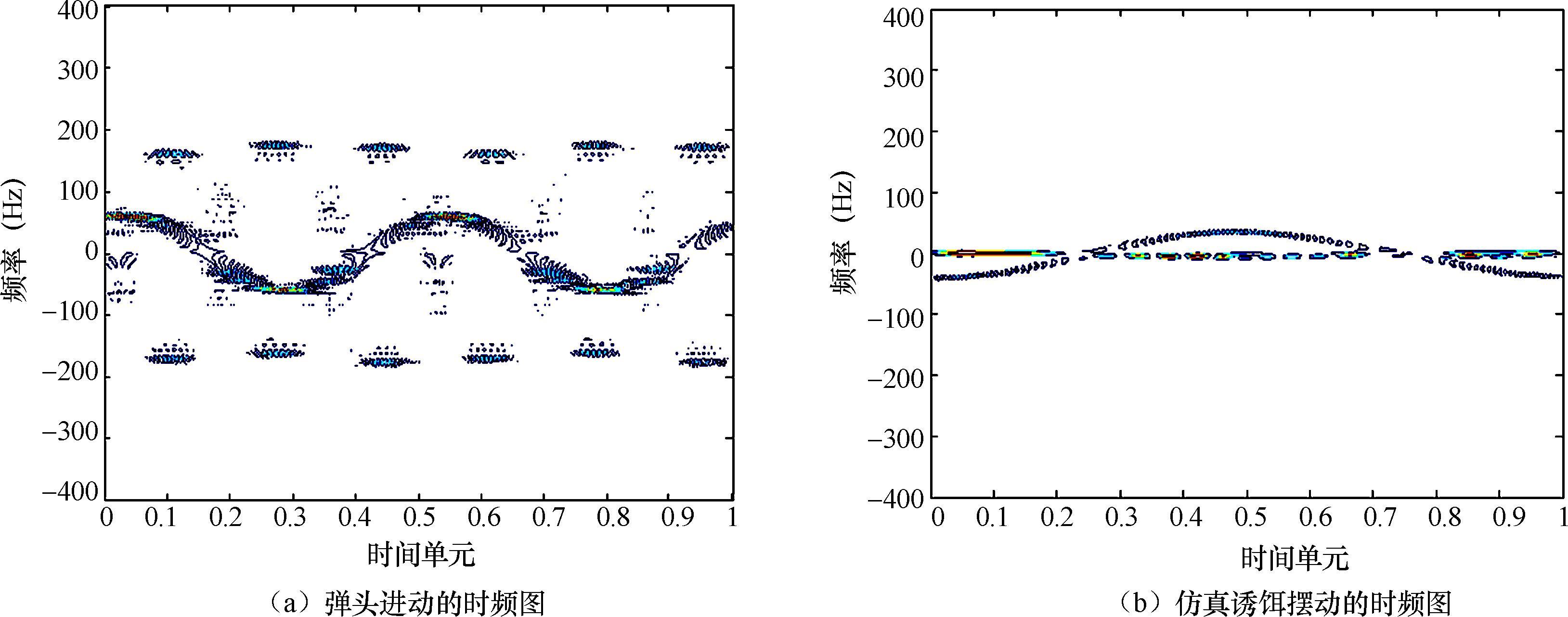
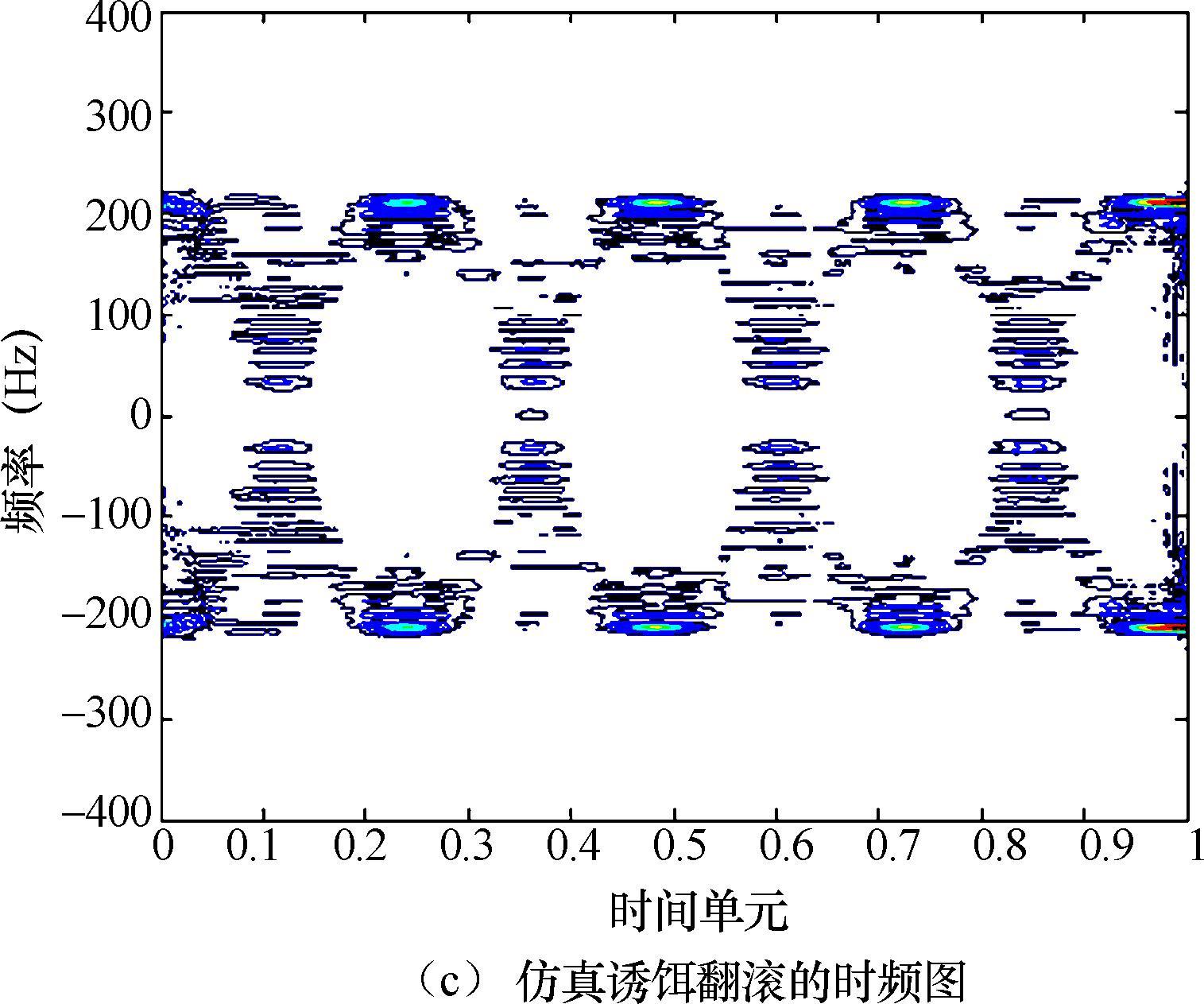
图2.12 导弹微动的时频图仿真
弹道目标在中段的微动会增加目标检测、目标成像和目标识别的难度。首先,弹道目标由于进动、章动和摆动等微动使得目标姿态角不断变化,导致目标回波的幅度起伏和相位的非线性变化,增加了积累检测的难度。其次,弹道目标在中段的微动增加了逆合成孔径雷达(ISAR)成像运动补偿的难度。在实际成像过程中,由于弹道目标的运动信息不完整,并且导弹的自身运动常伴有进动、章动等复杂运动,因此成像的平面会发生变化,造成成像困难。利用微动进行成像需要较高的采样率,目前的雷达很难满足这样的采样要求。最后,对于高分辨率雷达,由于微动弹道目标姿态不断变化,增加了对目标特征提取的难度。为了比较,图2.13给出了无微动和微动条件下导弹目标回波的多普勒谱,可以看出在微动时导弹多普勒谱被展宽,从而降低了相参积累的能量。
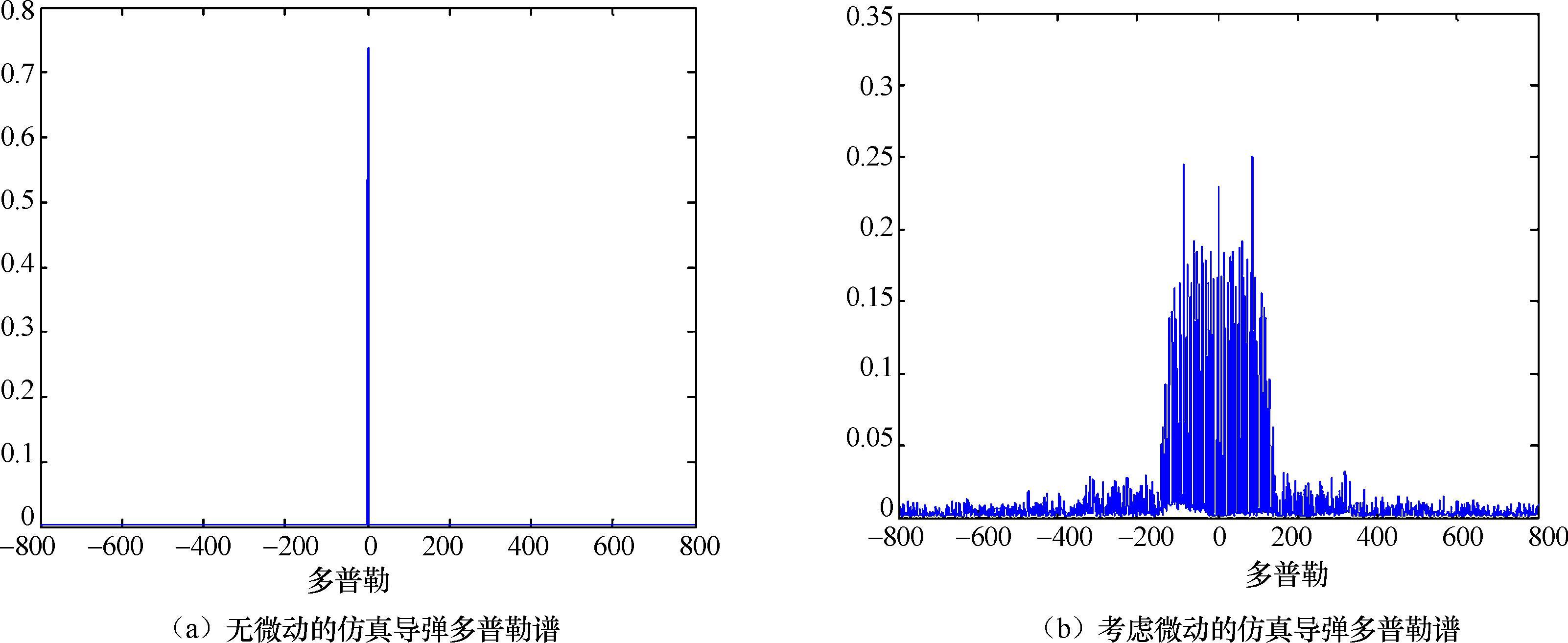
图2.13 无微动与微动条件下导弹目标回波的多普勒谱比较
如图2.14所示为无微动和存在微动条件下弹头目标ISAR成像比较,其中图2.14(a)为无微动时的导弹ISAR成像仿真结果,图2.14(b)为考虑弹道、自旋、锥旋时的导弹ISAR成像仿真结果,从中可以看出微动导致ISAR成像质量严重下降。
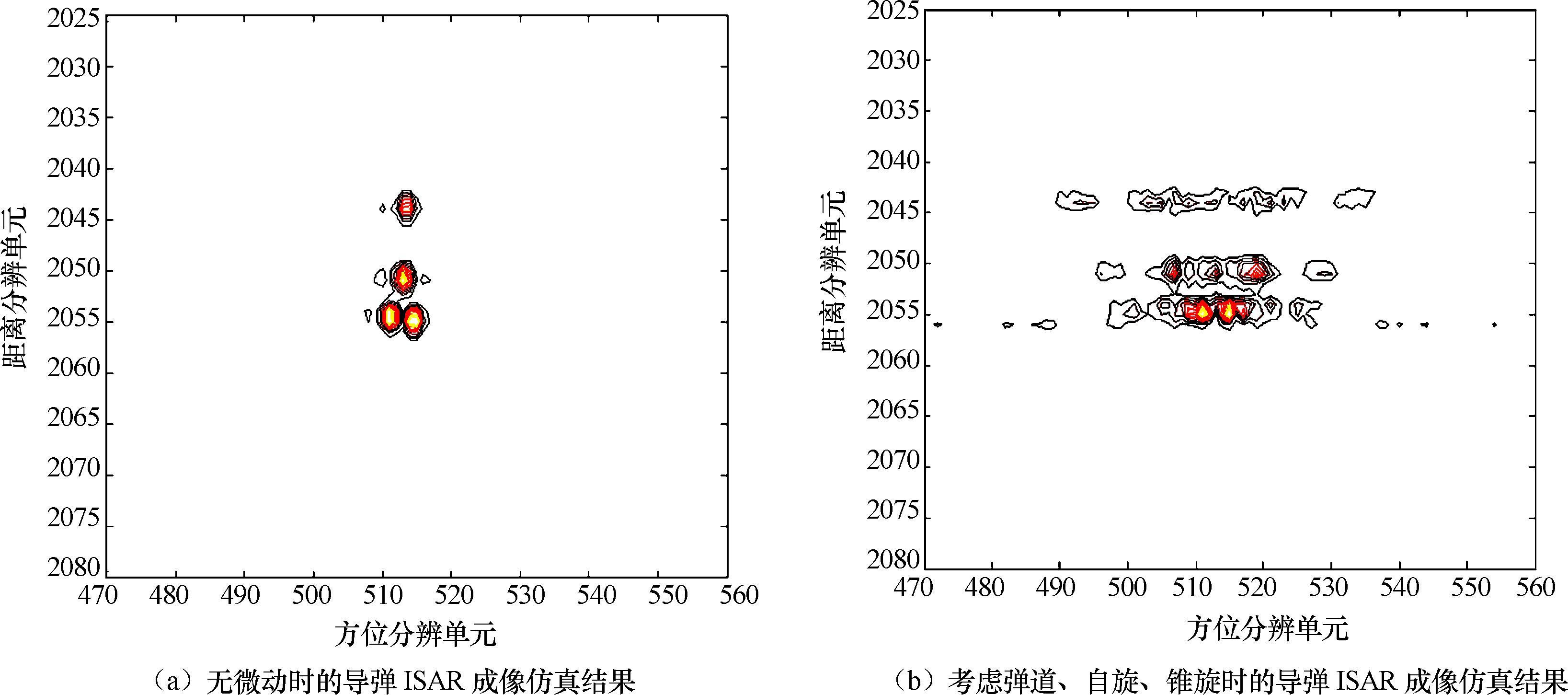
图2.14 无微动与微动条件下弹头目标ISAR成像比较
弹道导弹在沿弹道轨迹飞行时,弹头、诱饵、弹体等目标本身存在微运动(如振动、旋转、翻转、锥旋、摆动、进动和章动),这些微运动会对雷达回波产生微调制,形成附加的微多普勒频率。

图2.15 外太空充气诱饵
为了对抗与突防,美国“民兵-III”导弹携带有多种诱饵 [16] ,其中一种为外太空充气诱饵(IEO,Inflatable Exoatmospheric Object),如图2.15所示。IEO能够模拟真弹头的红外与雷达信号特征,具有非常高的逼真度。
由于IEO与真弹头具有相同的外形,IEO的静态RCS与真弹头静态RCS完全一样,因此单纯利用RCS无法区分真弹头与IEO,必须利用两者之间运动特性的差异进行识别。弹道导弹目标为了保证再入攻角,一般采用自旋定向,此时锥形目标易受扰动而产生进动或章动,这种运动方式是弹头目标所特有的运动特性。对于诱饵和其他碎片,由于没有姿态控制,目标会呈现翻滚等随机的运动方式。即使重诱饵和弹头的姿态运动形式类似,但弹头的质量较重诱饵大许多,和重诱饵相比,弹头进动角较小,进动周期较长,因此,弹头和重诱饵在自旋周期、进动周期、进动角等特征上存在较大差别,为识别提供了依据。结合目标的弹道运动和微动,对自旋弹头、重诱饵和翻滚弹体进行时频分析和频谱分析仿真。仿真条件如下:
(1) 弹头指向为再入方向,微动方式为进动,进动角为3°,自旋频率为3Hz,锥旋频率为1Hz;
(2) 诱饵指向弹道切线方向,微动方式为进动,进动角为15°,自旋频率为3Hz,锥旋频率为0.5Hz;
(3) 弹体沿弹道方向翻滚,翻滚频率为0.5Hz。
首先,需要计算雷达视线指向与目标自旋轴线之间的夹角。由于弹头、诱饵和弹体目标周期性运动,导致雷达天线波束指向与弹头自旋轴之间的夹角呈现周期性变化,如图2.16所示。
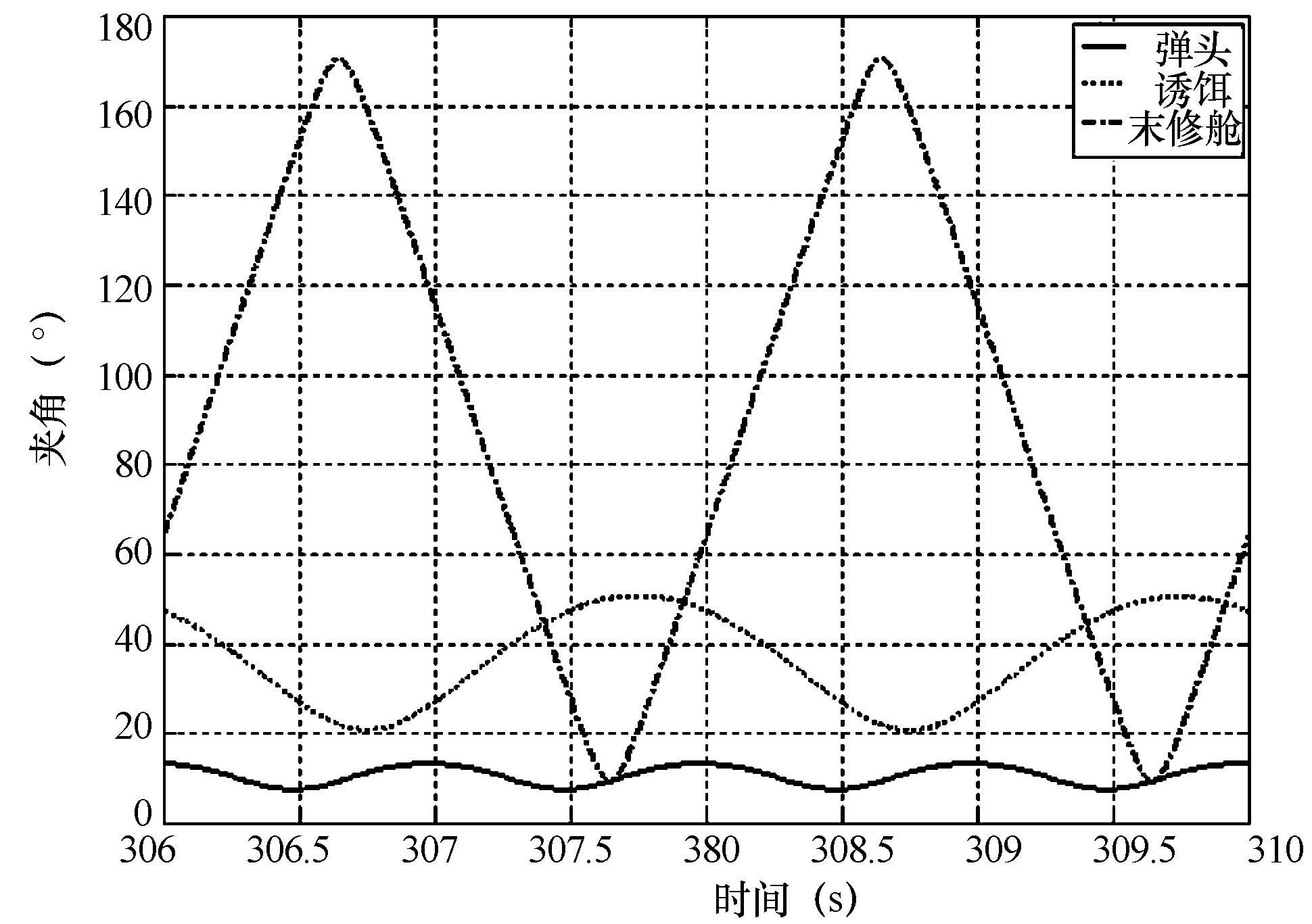
图2.16 雷达波束指向与目标自旋轴之间的夹角
对运动中所采集的目标RCS时间序列数据进行时频分析和频谱分析,获得弹头、诱饵、弹体目标的微多普勒信息,如图2.17所示。
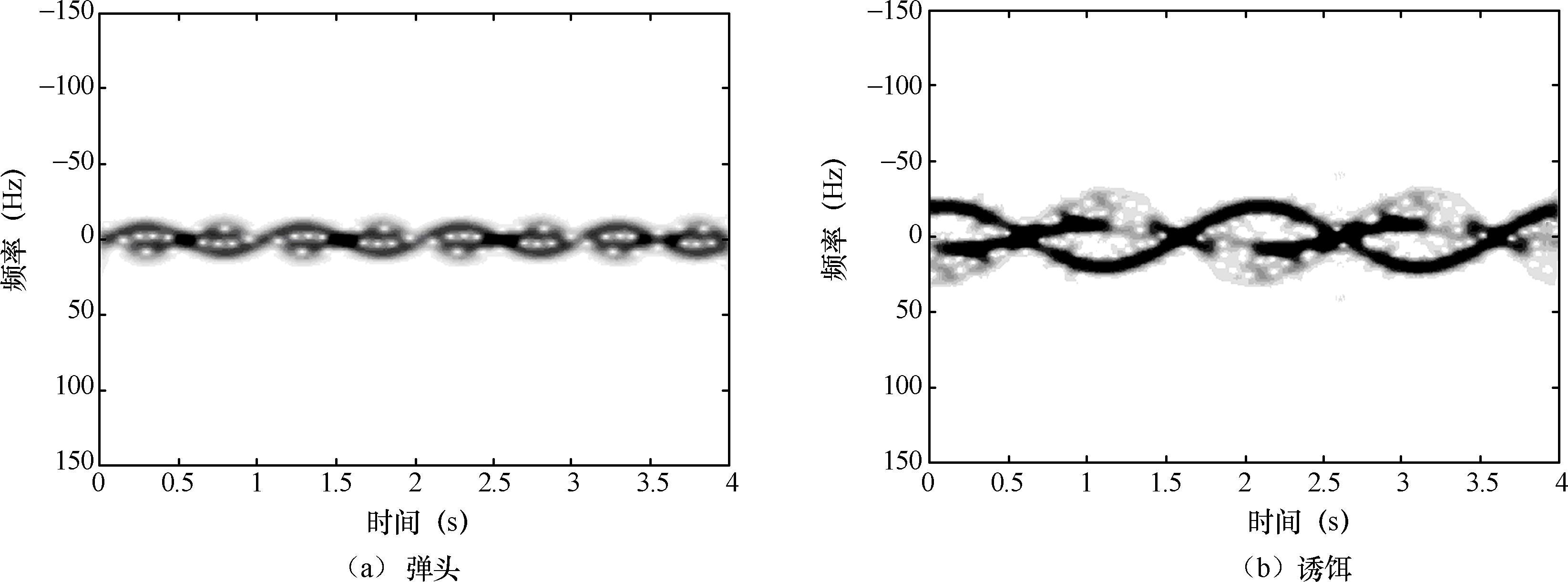
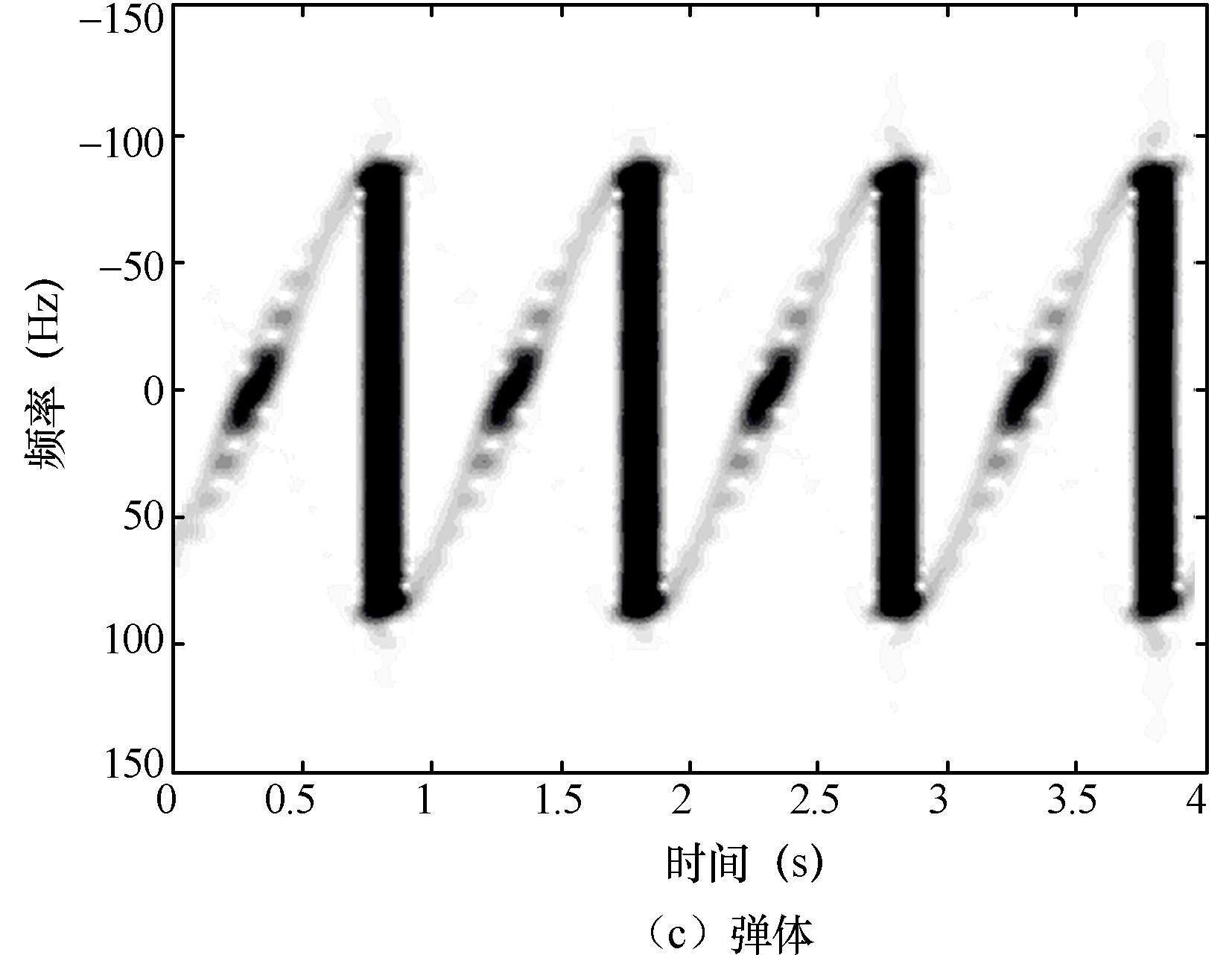
图2.17 导弹目标时频分析结果
由图2.18可见,诱饵与弹头相比,尽管二者外形尺寸一致,但由于目标运动指向、进动角、锥旋频率不同,相应的微多普勒频谱也不相同。
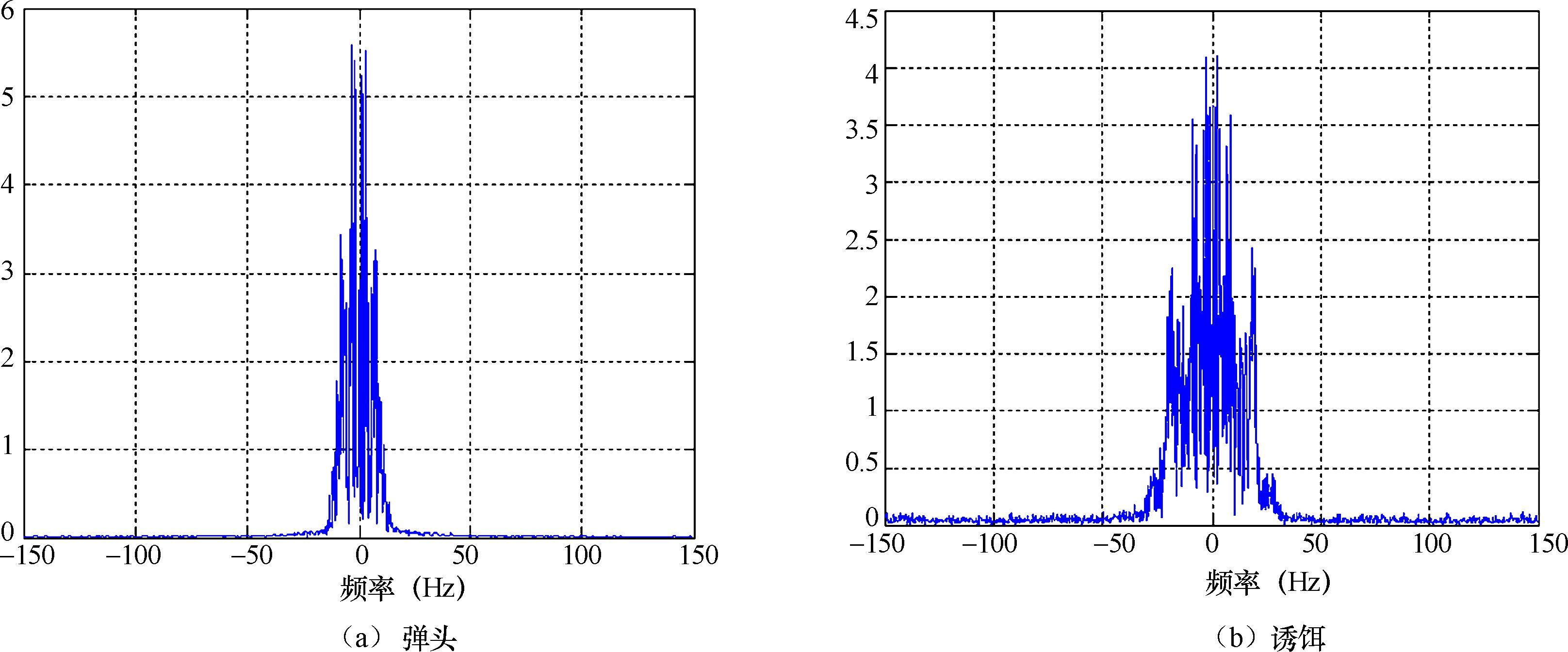
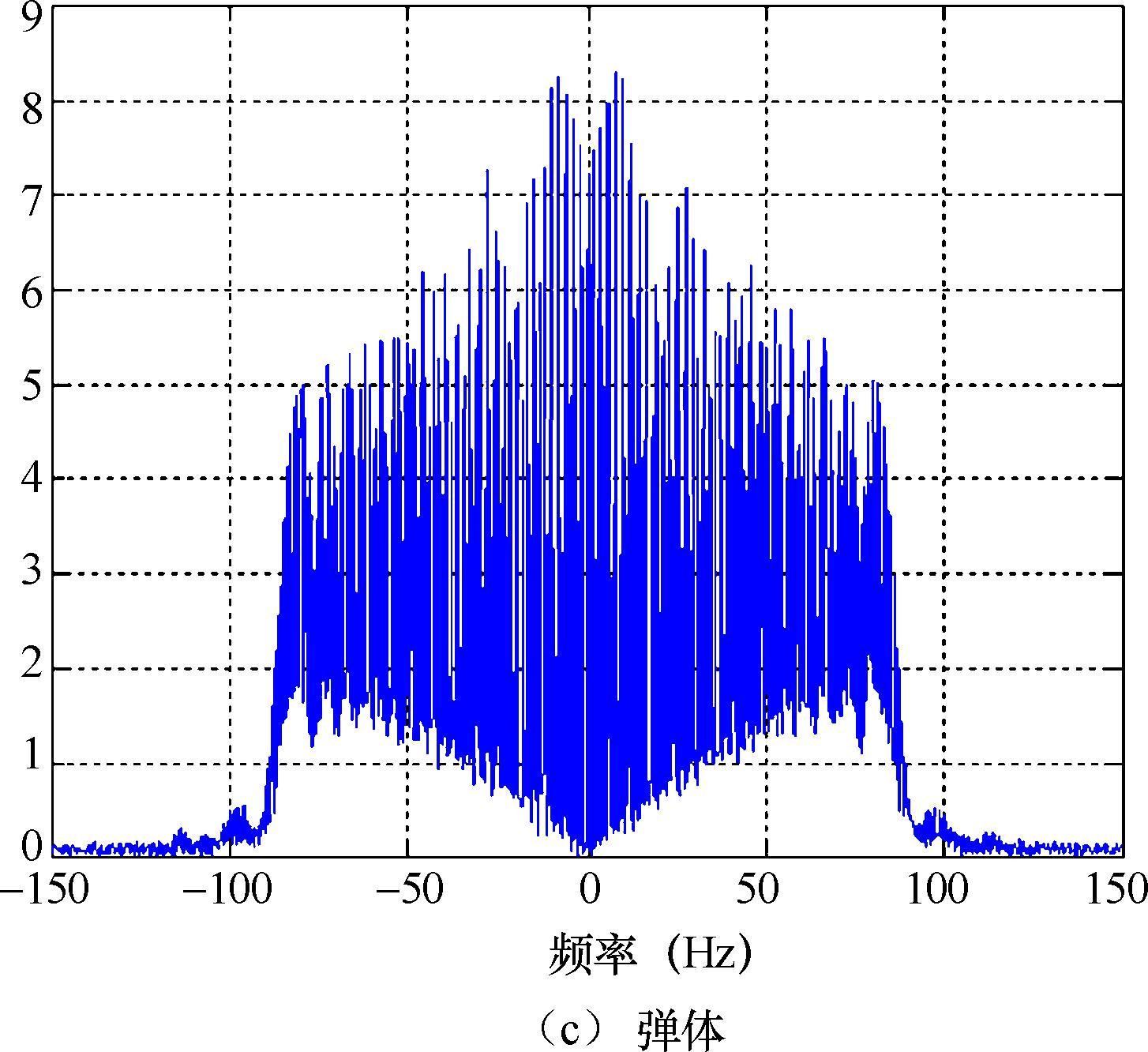
图2.18 导弹目标微多普勒频谱
弹体目标由于翻滚轴变化,可观测到弹体两侧平面,RCS序列出现突增现象。由于弹体在雷达入射方向上是对称的,RCS序列的微动周期设为1s,是仿真设置微动周期的一半。与进动目标相比,翻滚弹体目标的微多普勒谱宽更宽。