为了研究信号在局部时间段的频域特征，1946年Gabor提出了著名的Gabor变换，之后发展成为短时傅里叶变换（Short Time Fourier Transform，STFT）。其基本思想是对信号加窗，然后对窗内的信号进行傅里叶变换，因此它可以反映出信号的局部特征。STFT在实践中得到了广泛的应用。但由于STFT的定义决定了其窗函数的大小和形状与时间和频率无关，为固定窗函数的大小和形状（一般来说，实际中高频信号持续时间很短，而低频信号持续时间较长），因此希望能够对低频信号采用大时间窗进行分析，而对于高频信号采用小时间窗进行分析。小波变换继承了STFT的思想，它的窗口大小不变，但窗口形状可以改变，是一种时间窗和频率窗都可以改变的时频分析方法，即在低频部分具有较高的频率分辨率和较低的时间分辨率，在高频部分具有较高的时间分辨率和较低的频率分辨率，因此在时频域都具有很强的表征信号局部特征的能力 ^[27] 。

1.5.1 一维连续小波变换

定义 1.1 设φ（t）∈L ² （R），其傅里叶变换为φ（ω），当φ（ω）满足容许条件（完全重构条件或恒等分辨条件）

时，称φ（t）为一个基本小波或母小波。将母小波φ（t）经伸缩和平移后得：

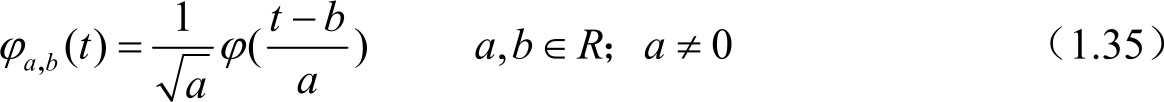
称其为一个小波序列。其中，a为伸缩因子，b为平移因子。

对于任意函数 f （t）∈L ² （R）的连续小波变换为：

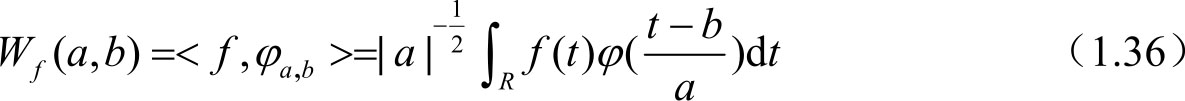
其重构公式（逆变换）为：

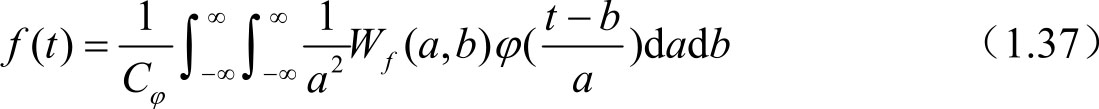
由于基本小波φ（t）生成的小波序列φ _{a ， b} （t）在小波变换中对被分析信号起着观测窗的作用，因此φ（t）还应该满足一般函数的约束条件：

故φ（ω）是一个连续函数。这意味着为了满足完全重构条件，φ（ω）在原点必须等于0，即

为了使信号重构的实现在数值上是稳定的，除了满足完全重构条件外，还要求小波φ（t）的傅里叶变换满足下面的稳定性条件：

式中，0＜A≤B＜∞。

从稳定性条件可以引出一个重要的概念。

定义 1.11 若小波φ（t）满足稳定条件，则定义一个对偶小波 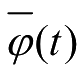，其傅里叶变换 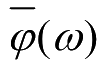为：

从式（1.41）可以看出，稳定条件实际上是对分母的约束条件，它的作用是保证对偶小波的傅里叶变换存在。

值得注意的是，一个小波的对偶小波一般不是唯一的，然而在实际应用中通常希望一个小波具有唯一的对偶小波。因此寻找具有唯一对偶小波的合适小波就成为小波分析的基本问题之一。

通过总结我们可以看出，连续小波变换主要具有以下重要性质：

（1）线性：一个多分量信号的小波变换等于各个分量的小波变换之和。

（2）平移不变性：若f （t）的小波变换为W _f （a，b），则 f （t-τ）的小波变换为：

（3）伸缩公变性：若f （t）的小波变换为W _f （a，b），则 f （ct）的小波变换为：

（4）自相似性：对应不同尺度参数a和不同平移参数b的连续小波之间是自相似的。

（5）冗余性：连续小波变换中存在信息表述的冗余。

1.5.2 离散小波变换

在实际运用中，尤其是在计算机上实现时，连续小波变换必须加以离散化。因此，有必要讨论连续小波序列φ _{a ， b} （t）和连续小波变换W _f （a，b）的离散化。

在连续小波中，考虑函数：

式中，b∈R，a∈R ₊ ，且a≠0，φ是容许的，为了方便起见，在离散化中，总限制a只能取正值，这样相容性条件就变为：

通常，把连续小波变换中尺度参数 a 和平移参数 b 的离散化公式分别取作 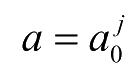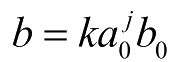， ，这里 j∈Z，扩展步长a ₀ ≠1是固定值，为方便起见，总是鉴定a ₀ ＞1 （由于m可以取正也可以取负，因此这个鉴定无关紧要）。所以对应的离散小波函数φ _{j ， k} （t）即可写作：

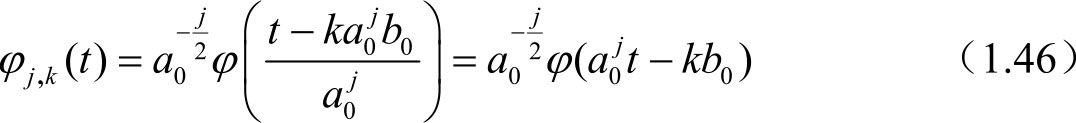
而离散化小波系数则可表示为：

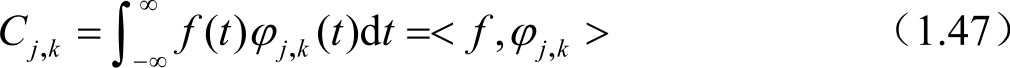
其重构公式为：

C是一个与信号无关的常数。 xF48AebJ41PPQbbfabZeaB80HX2ZckSjxm0oXcYeAdoPJqVT6UNvE1uAtdCAsUrp