




(1)方程:含有未知数的等式称为方程。
(2)方程的元:方程中含有未知数的个数。
(3)方程的次:方程中含有未知数的最高次幂的次数。
(4)方程的解:使方程左右两边相等的未知数的值称为方程的解。
(5)解方程:求方程解的过程称为解方程。
(6)方程组:由几个方程联立组成的一组方程,称为方程组。
(7)方程组的解:方程组里所有方程的公共解,称为方程组的解。
(8)解方程组:求出方程组的解或证明它们无公共解的过程,称为解方程组。
(1)移项:把方程中的已知项从方程的一边移到另一边,这种变形称为方程的移项。
(2)多项式中单项式移项(俗称左右移项):当一个单项式从一边移到另一边后,其符号要变号(+变-,-变+)。
(3)单项式的移项(俗称上下移项):当等式两边为分式形式存在时,分子项移到另一边变成分母项,而分母项移到另一边变成分子项。
【例14】 通过移项整理下列方程。
(1)3(x-(2x(x+1)))=2(1-x)
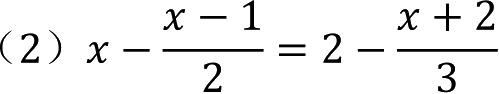
解: (1)3x-6x 2 -6x=2-2x
3x-6 x 2 -6x+2 x-2=0
-6x 2 -x-2=0
6x 2 +x+2=0
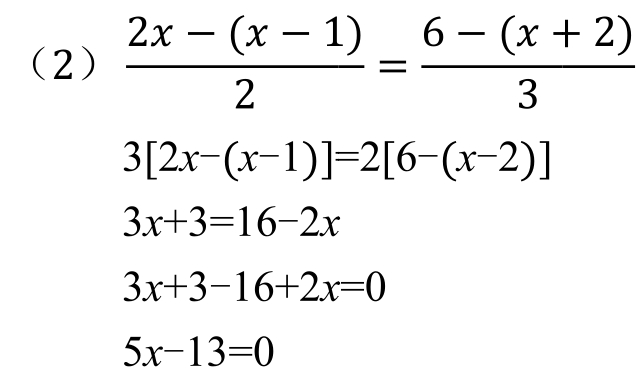
【例15】 整理方程,使左边为含未知数项,右边为常数项。
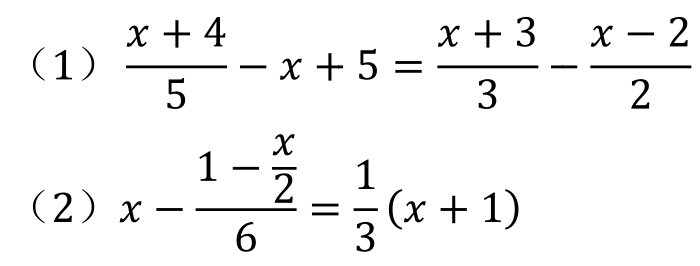
解: (1)6[(x+4)x+25]=10(x+3)-15(x-2)
6(x 2 +4x+25)=60-5x
6x 2 +2 4x+150=60-5x
6x 2 +2 9x=-90
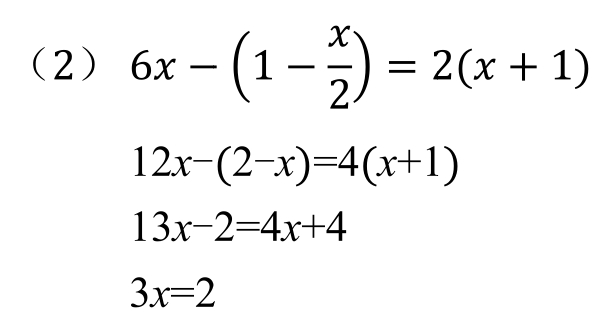
【例16】 解方程。
(1)10x+3=3(2x+1)-(3-x)
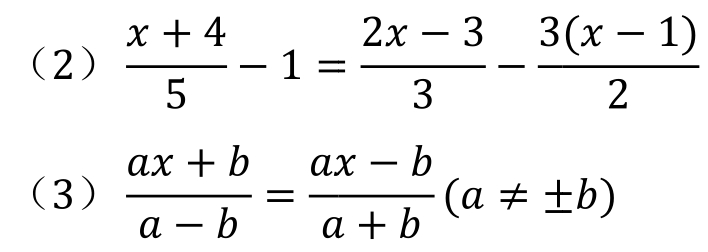
解: (1)去括号 10x+3=6x+3-3+x
移项 10x-6x-x=3-3-3
合并同类项 3x=-3
x=-1
(2)两边乘以30

(3)此类含有字母的方程,字母a,b要看作已知数,未知数是x。
乘除移项(a+b)(ax+b)=(a-b)(ax-b)
去括号 a 2 +ab+abx+b 2 =a 2 x-abx-ab+b 2
移项,合并同类项 2abx=-2ab
x=-1
1.解方程:
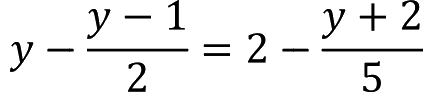
2.解方程:3[x-2(x-1)]=2(1-x)
3.解方程:m(nx-2)=2(mx-3)+n(m≠0,n≠2)
方程中只有一个未知数,且未知数的最高次幂为 1的方程,称为一元一次方程。
一元一次方程通过去分母、去括号、移项、合并同类项等步骤以后,都可以化成标准形式:
ax=b 或
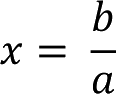
当a≠0时,方程有唯一解x=b/a。
当a=0,b≠0时,方程无解。
当a=0,b=0时,方程有无数个解。
一元一次方程常常用来求解电路中的未知量,因为电子电路中很多定理、定律都属于一元一次方程的范畴,例如,欧姆定律、基尔霍夫电流定律、基尔霍夫电压定律和叠加定理、等效电源定理等。往往把定律中某一参数设置为未知数,通过其他参数列出一元一次方程求解,下面通过几个例子给予说明。
【例17】 图1-4所示为发光二极管电路,设发光二极管正向压降为2.3V,导通电流为5mA,电源E=24V,求限流电阻R值。
解: 由基尔霍夫电压定律得
E=I · R+VD(一元一次方程)
则
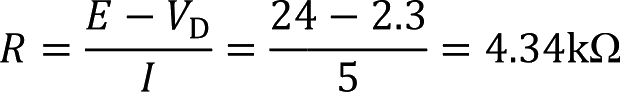
可选R=4.3kΩ。
【例18】 如图1-5所示,I=2A,E 1 =48 V,R 1 =R 2 0.5Ω,R 3 =6Ω,R 4 =5Ω,求E 2 的大小和极性。
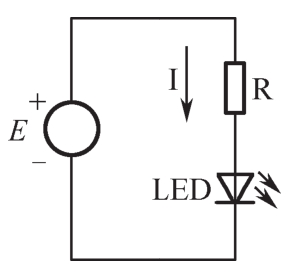
图1-4 例17图
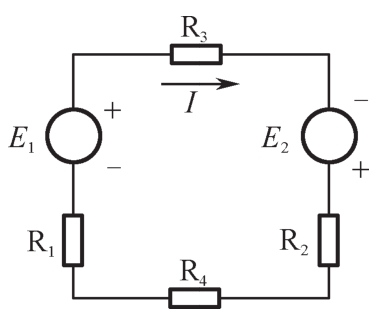
图1-5 例18图
解: E 2 的极性不知道,但不是上正下负,就是下正上负,根据1.1.2节所讲,先假设一正方向。例如,下负上正,如图1-5所示。
由基尔霍夫电压定律列顺时针回路方程,得
E 1 =IR 3 +(-E 2 )+IR 2 +IR 4 +I R 1
E 1 =I(R 1 +R 2 +R 3 +R 4 )-E 2
E 2 =I(R 1 +R 2 +R 3 +R 4 )-E 1
E 2 =2×12-48=-24V
E 2 的电压为24V,极性与假设相反,是上正下负。
方程中只有一个未知数,且未知数的最高次幂为2的方程,称为一元二次方程。
一元二次方程通过去分母、去括号、移项、合并同类项等步骤以后,都可以化成标准形式:
ax 2 +bx+c=0(a≠0)
一元二次方程的求解方法有因式分解法、配方法和公式法等,这里仅介绍公式法求解。
设一元二次方程的解为x 1 ,x 2 ,则其解为
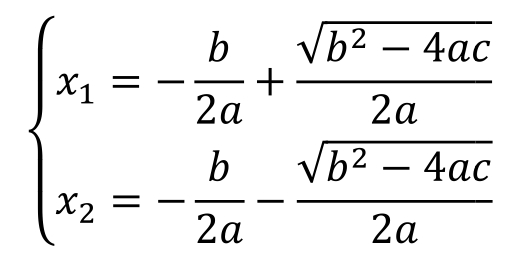
设Δ=b 2 -4ac,则有:
Δ>0,有两个不同的实数解;
Δ=0,有两个相同的实数解;
Δ<0,方程无实数解。
当x 1 ,x 2 为方程a x 2 +bx+c=0(a≠0)的两个解时,则下面关系式成立。
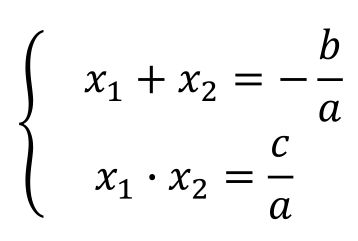
【例19】 用公式法解方程:3 x 2 +2x-8=0。
解: 依题意有a=3,b=2,c=-8。
代入公式,得
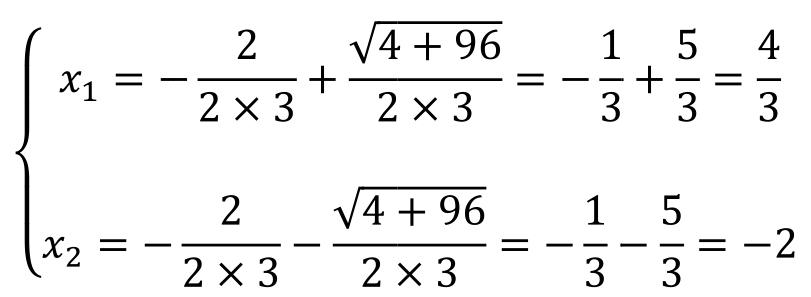
【例20】
当k为何值时,方程
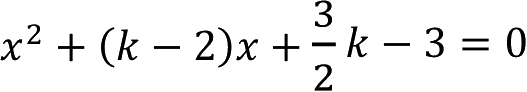 有两个相等的实数解。
有两个相等的实数解。
解: 依题意Δ=0时,方程有两个相等的实数解。
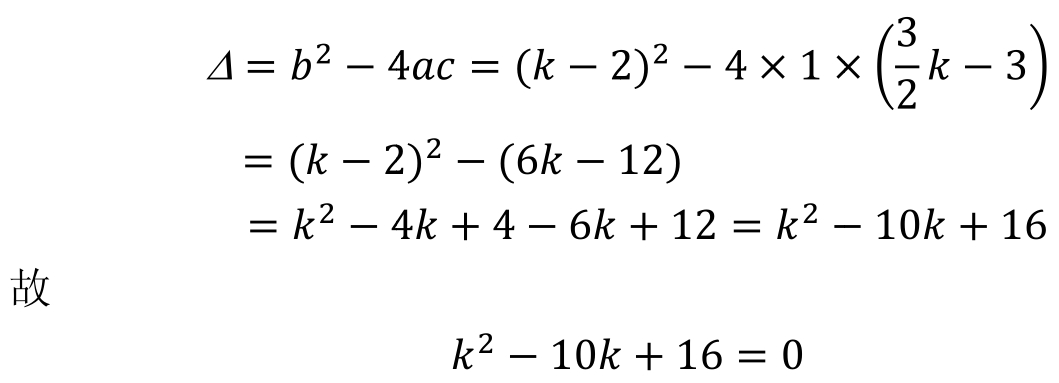
按公式法解出k 1 =8,k 2 =2。
即当k=8或k=2时,方程有两个相等的实数解。
【例21】 已知方程3x 2 +6x-2=0的两个解为x 1 ,x 2 ,不解方程,求下列各式的值。
(1)
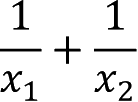 (2)x 1
2
+x2
2
(2)x 1
2
+x2
2
解: 由韦达定理可知
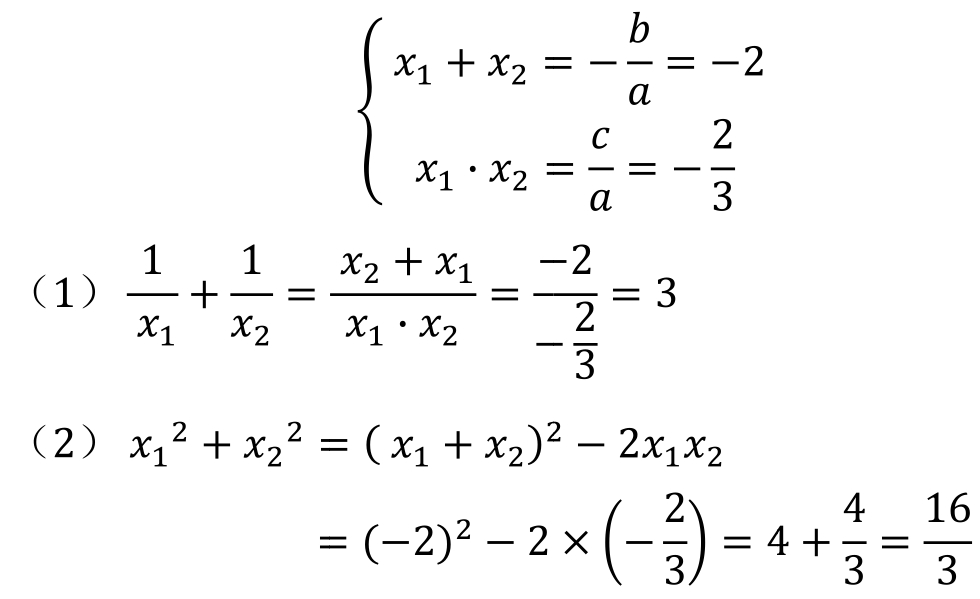
1.公式法解方程4(x+1) 2 =9(2x-3) 2 。
2.试判断方程4 x 2 -x+3=7x 解的情况。
3.已知一元二次方程的两个解9和-1,求该一元二次方程。
4.已知方程3x
2
-2x-1=0的两个解x
1
,x
2
,在不求出解的情况下,求
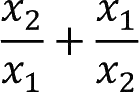 的值。
的值。
方程中含有两个未知数,且各未知数的最高次幂均为1的方程,称为二元一次方程,由两个二元一次方程组成的方程组称为二元一次方程组,其一般形式为
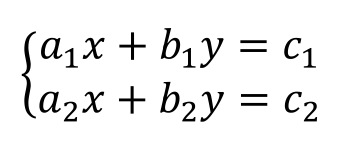
(1)二元一次方程组的解满足两个方程的左右两边值相等的两个未知数的值(称之一组解)。
(2)二元一次方程组常用解法有代入法、加减消元法和行列式法。
下面举例说明代入法和加减消元法的应用。
【例22】 试用代入法求解二元一次方程组
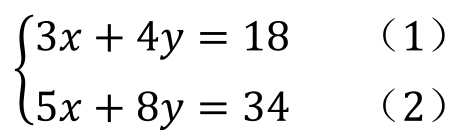
解: 代入法是在方程组中选出一个方程,然后用一个未知数的代数式表示另一个未知数,并把这个代数式代入另一个方程中,使另一个方程变成一个一元一次方程进行求解。解出一个未知数后,再通过代数式或代入原方程中求出另一个未知数。
选式(1),用x的代数式表示y,有
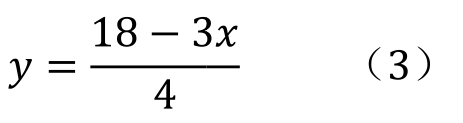
将式(3)代入式(2),得
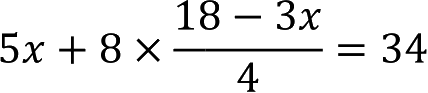
整理,得
5x+36-6x=34
-x=-2
解得
x=2
把x=2代入式(3),解得
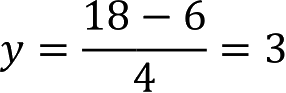
所以方程组的解为
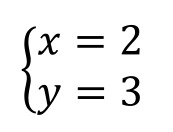
【例23】 用加减消元法求解二元一次方程组
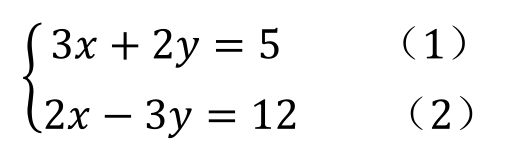
解: 加减消元法是指把方程组中一个未知数通过合理算法消去,转化成另一个未知数的一元一次方程进行求解。当同一未知数的系数符号相同时,用减法消元,当同一未知数的系数符号不同时,用加法消元。题中的x的系数相同,可以用减法消去x,而y的系数正好相反,用加法消元。试用加法消元消去y。
式(1)×3,并式(2)×2,有
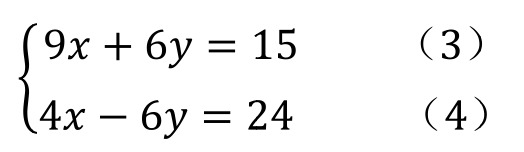
式(3)+式(4):13x=39
解得
x=3
将x=3代入式(1):3×3+2y=5
2y=-4
解得
y=-2
所以方程组的解为
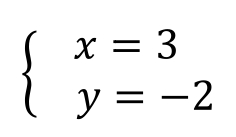
试分别用代入法和消元法求解下面二元一次方程组:
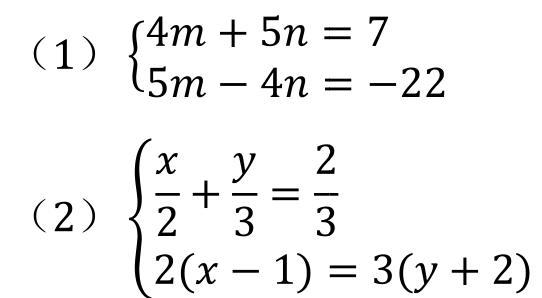
方程中有n个未知数且未知数的最高次幂为1,称为一元n次方程。由n个n元一次方程所组成的方程组,称为n元一次方程组,也称n元线性方程组。
n元线性方程组不能采用在二元一次线性方程组中所介绍的代入法和消元法进行求解,因为那样工作量太大。一般采用线性代数理论进行求解。这里不作介绍,读者可参阅相关资料。
在线性电路中,不管电路多么复杂,总是由许多支路组合而成的。而各条支路在电路上会组成许多节点(三条或三条以上支路的汇合点)和网孔(其中不含支路的闭合电路)。节点和网孔都可以根据基尔霍夫电流定律和基尔霍夫电压定律写出相应的n元一次方程,由这些n个一次方程组成的n元一次线性方程组,便是电路的解(节点电压或支路电流)。数学在这里发挥了巨大的作用。
【例24】 图1-6所示为某汽车等效电路图,图中,E G 为硅整流发电机,R G 为其内阻,E B 为蓄电池,R B 为其内阻,R L 为汽车用电器(灯,喇叭)总和。
设E G =18V,R G =1Ω,E B =12V,R B =2Ω,R L =10Ω。
(1)蓄电池工作在电源状态还是负载状态?I B =?
(2)欲使发电机I G =0,则E G =?
(3)欲使蓄电池以5A电流充电,则E G =?
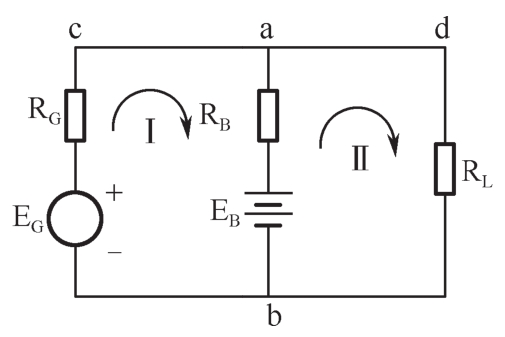
图1-6 汽车等效电路图
解: (1)用基尔霍夫定律列方程
对节点a有I G =I B +I L
对回路Ⅰ有I G R G +I B R B =E G -E B
对回路Ⅱ有I L R L -I B R B =E B
将数据代入,并整理有三元一次方程组
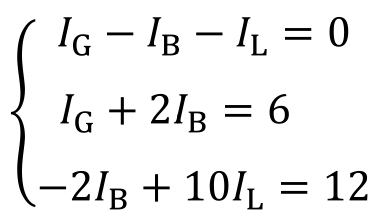
解方程,得
I B =1.5A
I B 为正值,方向与图中一致,蓄电池处于充电状态。
(2)当I G =0时,仅回路Ⅱ在工作,且I B =-I L ,对回路Ⅱ有E B =-I B R B +I L R C
=I L R B +I L R L =I L (R B +R L )
解得
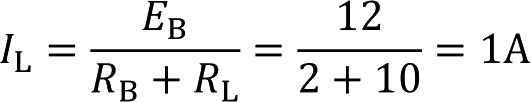
则
U ab =U ab =I L R L =1×10=10V
由
U ab =U ab =-I G R G +E G
因为
I G =0
所以
E G =U a b =10V
(3)将I B =5A代入方程组,有
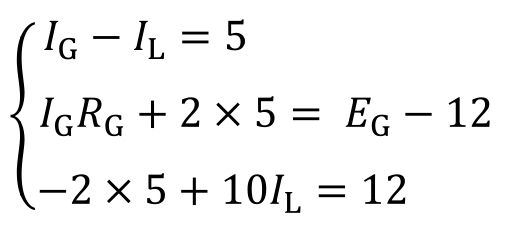
解得
E G =29.2V