




数轴上的每一个点都表示一个实数,而每一个实数都可以在数轴上找到其对应的点,这就是数轴上的点和数的一一对应关系。数轴上的数都是相对于原点距离来确定的,原点可以称为起点或参考点,这就是数轴上点的位置确定方法。如果一个点在平面上,那么它的位置是如何确定的呢?有两种主要方法可以确定平面上点的位置。
(1)直角坐标法:如图2-1(a)所示,在平面上作两条互相垂直的线(坐标轴),点P是平行于两个坐标轴的直线的交点,交点坐标值(x,y)就是点P的位置。
(2)极坐标法:如图2-1(b)所示,在平面上作一条射线OX,连接OP,则OP的距离和其与射线之间的夹角(r,θ)就是点P的位置。
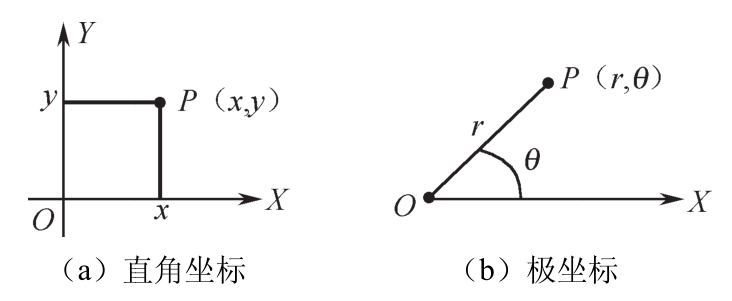
图2-1 两种坐标
上面两种方法说明,平面上的点,其位置必须用两个数才能确定。本章仅讨论直角坐标法,极坐标法会在第3章中介绍。
(1)定义:在平面内,两条互相垂直且有公共原点的数轴组成平面笛卡儿坐标系。水平的数轴称为X轴或横轴,垂直的轴称为Y轴或纵轴。两条轴的交点O称为坐标原点,如图2-2所示。
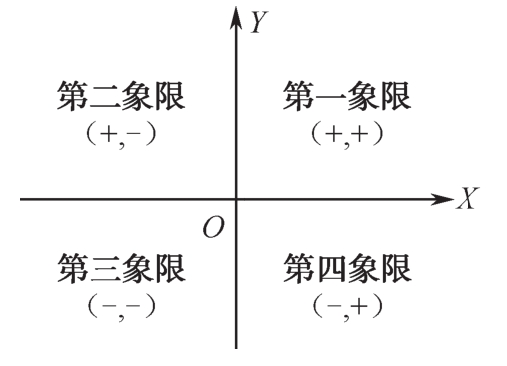
图2-2 平面笛卡尔坐标系
(2)象限:平面笛卡儿坐标系把整个平面分成4个部分,分别称为第一象限、第二象限、第三象限和第四象限,平面上所有的点均落在这四个象限的一个象限内,如图2-2所示。
(1)对平面内任意一点P,过P点分别向X轴和Y轴作垂线,垂足在X轴及Y轴上的对应的数x、y分别称为点P的横坐标、纵坐标。有序数对(x,y)称为P点坐标,如图2-1(a)所示。
(2)平面内的点都可以用其坐标(x,y)来表示,并且点和坐标(x,y)存在一一对应关系,即每一个平面内的点只能有一个坐标(x,y)表示,每一个坐标数(x,y)只能表示一个点。
(3)点在4个象限内的坐标值的符号是一定的。例如,在第一象限内,坐标值x>0,y>0均为正值,用(+,+)表示。在第三象限内,坐标值x<0,y<0。用(-,-)表示。同理,在第二象限为(-,+),第四象限为(+,-)。只要知道点的坐标值,就知道它在第几象限,如图2-2所示。
(4)特殊点的坐标。
笛卡儿坐标系中有几个特殊点的坐标,如图2-3所示。这些特殊点为:
●原点坐标(0,0),如图2-3的O点。
●X轴上点坐标(x,0),如图2-3的A点。
●Y轴上点坐标(0,y),如图2-3的B点。
●平行于X轴的直线上点坐标(x,a),如图2-3的点C。
●平行于Y轴的直线上点坐标(b,y),如图2-3的点D。
特殊点的坐标要求能记住。
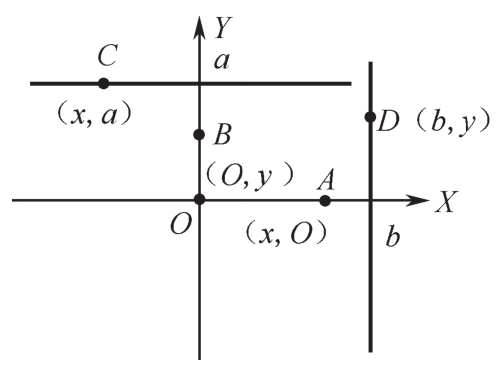
图2-3 特殊点坐标
(1)对称点坐标指与点关于轴对称和原点对称的坐标,设平面上点的坐标为(x,y),则其关于X轴的对称点的坐标为(x,-y);关于Y轴的对称点的坐标为(-x,y),关于原点的对称点坐标为(-x,-y),如图2-4所示。
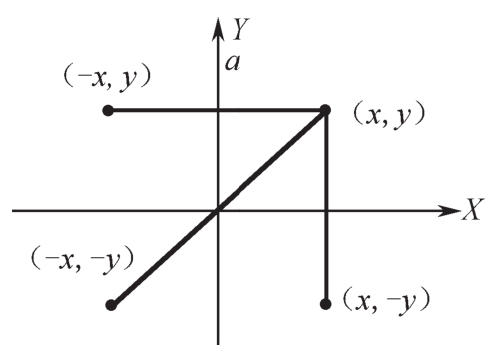
图2-4 对称点坐标
(2)点到直线,点到点的距离公式。
设平面上点的坐标为(x,y),则点到X轴的距离为|y|,点到Y轴的距离为|x|,点到原点O的距离公式为
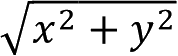 。
。
平面上有两个点A(x 1 ,y 1 )和B(x 2 ,y 2 ),则两点的距离为
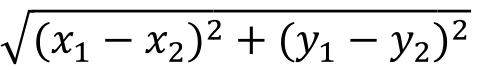
【例1】 若点P(a,5-a)是第二象限的点,求a值的取值范围。
解: 第二象限点为(-,+),则
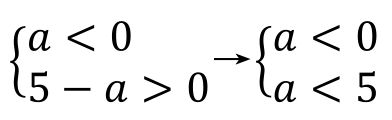
所以
a<0
【例2】 坐标平面内点P(-3,6),试写出对称点坐标,并指出它们在第几象限。
解: X轴对称点坐标(-3,-6)第三象限
Y轴对称点坐标(3,6)第一象限
原点对称点坐标(3,-6)第四象限
【例3】 试求点P(4,-6)到坐标轴及原点距离。
解: 到X轴距离为|-6|=6
到Y轴距离为|4|=4
到原点距离为
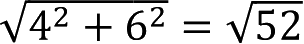
1.指出下列各点在哪一个象限内。
A(4,-6)B(-3,-8)C(-10,
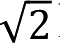 )
)
2.如果点A(2,y 1 )和点B(x,-3)为关于X轴的对称点,求A点和B点的坐标。
3.点(2,-3)和点(10,-7)的距离是多少?