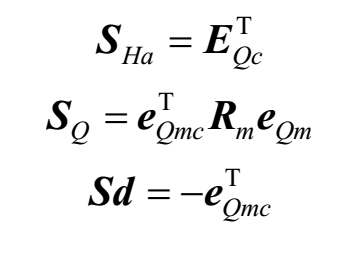为了建立状态方程，必须找到系统状态的独立变量。不难发现通过树和连支的概念可以很容易实现。根据图论原理，借用树和连支的概念，首先定义通风网络的树，使之包含执行机构分支，取连支流量作为状态变量。为了便于分析，标志连支从1到l=N-n _c +1，N=n+g为包含执行机构的分支个数，非执行机构树枝从l+1到n，执行机构树枝从G ₁ 到G _g 。

定义：

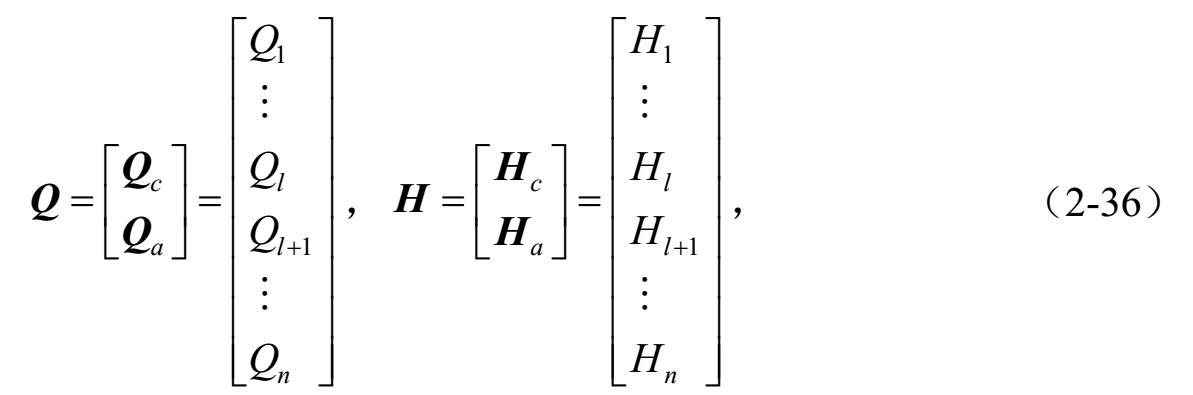
即 Q _c 和 H _c 矩阵分别描述连支中的流量和压降， Q _a 和 H _a 矩阵分别描述树枝中的流量和压降，但并不包括执行机构的分支。

定义 Q _D 和 K 如下：

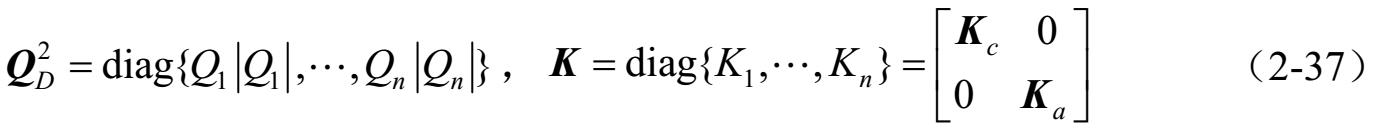
则式（2-24）可以重新写为：

命题2.1 ：存在维数一定的矩阵 A , B , C , Y _RQ , Y _Q 和 Y _d ，使得流体网络全阶模型可以表示为：

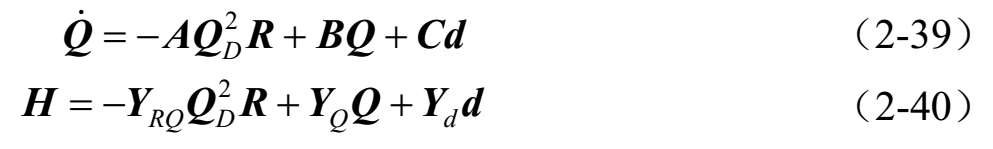
式中， Q 是系统的状态； R 和 d 是输入； H 是系统的输出。

证明：

矩阵 E _H ， E _Q ， e _Hm 和 e _Qm 可用如下形式来表示：

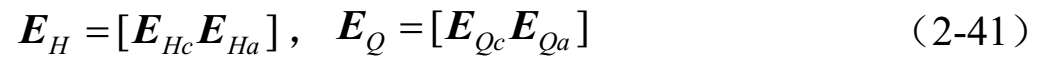
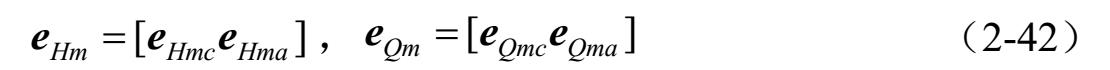
式中，

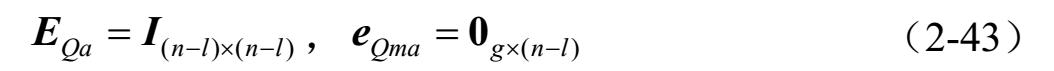
现在通过连支的流量来表示树枝的流量，由式（2-26）、式（2-36）和式（2-41）得：

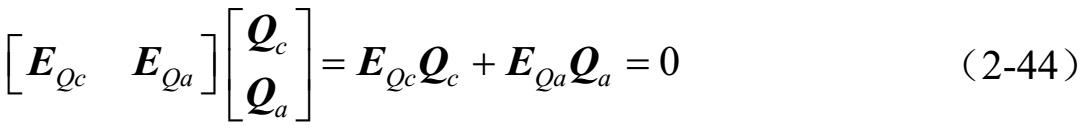
由式（2-43）中的E _Qa =I( _n-l)×(n-l) 知：

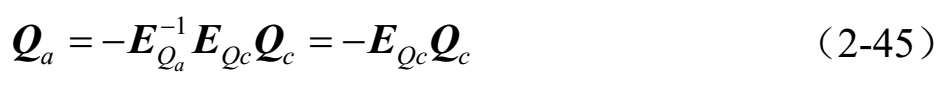
由式（2-30）和式（2-32）可得：

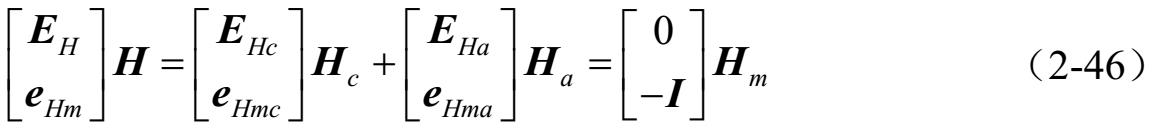
因此，如果 的逆存在（详见引理2.1），则H _c 表示如下：

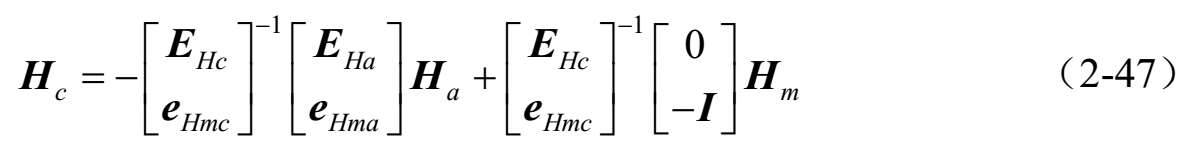
通过式（2-35），重写式（2-47）如下：

式中：

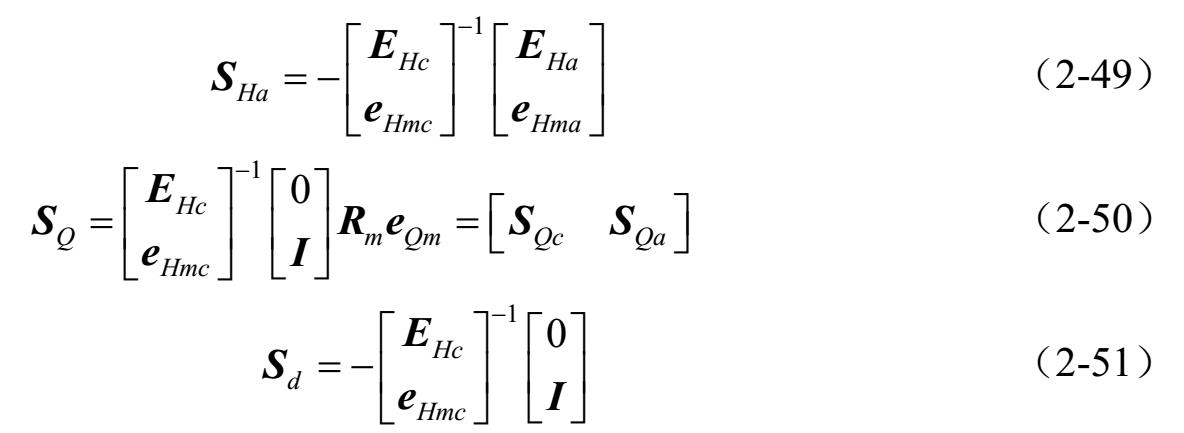
微分 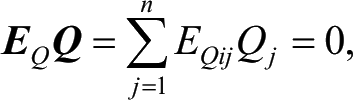可得 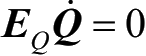，由式（2-37）和式（2-38）可得：

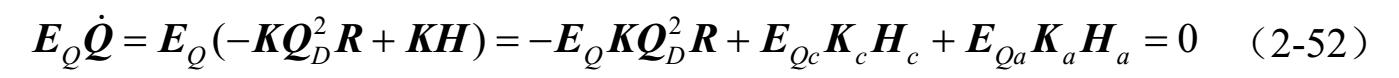
由式（2-52）和式（2-48）可得：

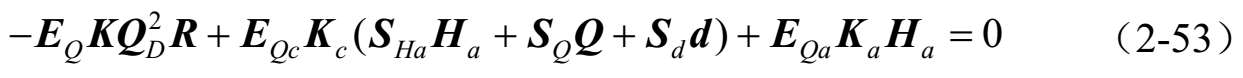
由式（2-43）得：

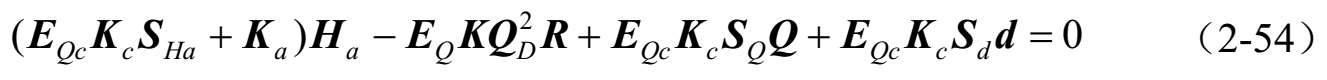
因此

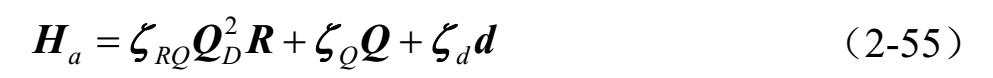
式中：

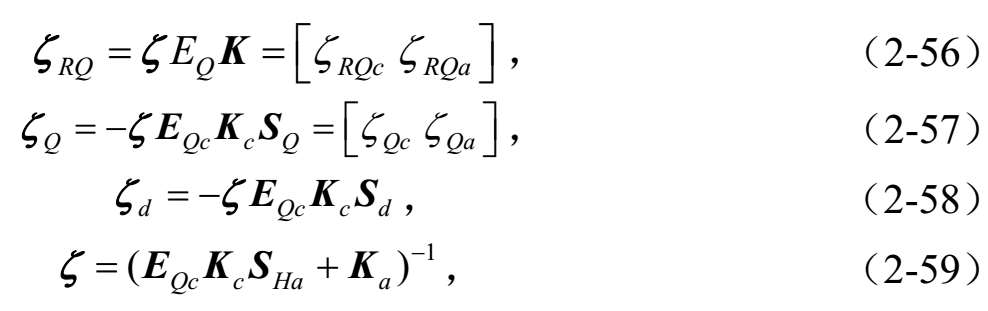
其中，式中( E _Qc K _c S _Ha + K _a )的逆存在，证明详见引理2.2。

把式（2-55）代入式（2-48）得：

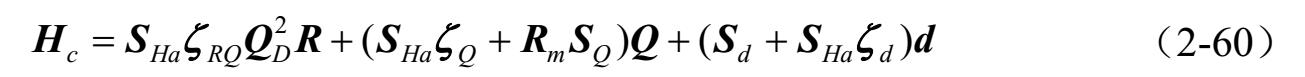
由式（2-36）、式（2-55）、式（2-60）得：

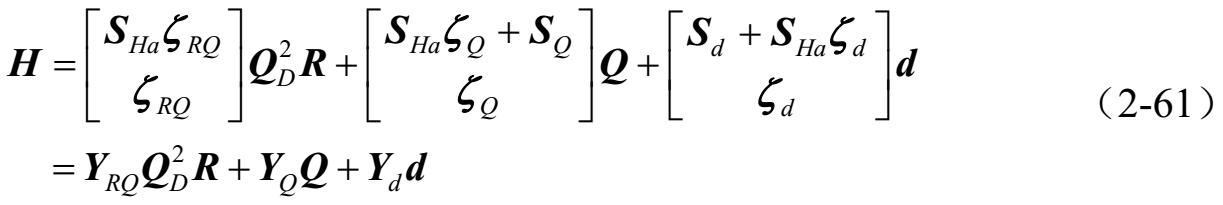
式中：

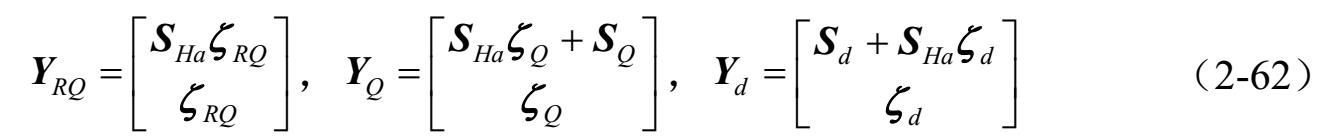
把式（2-61）代入式（2-38）可得：

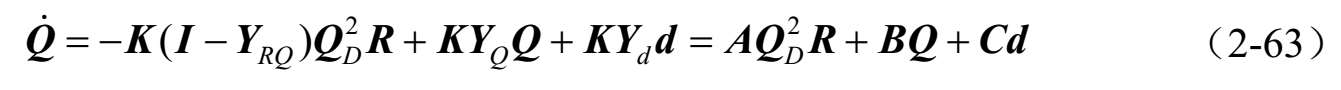
式中：

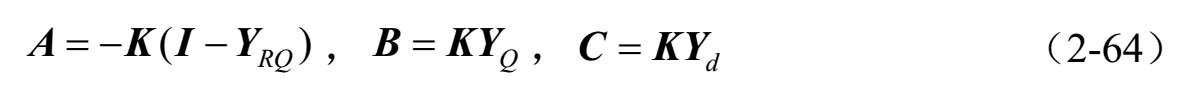
从而建立了以所有分支流量 Q 为系统的状态，压力 H 为系统的输出的流体网络全阶模型。

引理2.1 ：矩阵 的逆存在。

证明：

由参考文献[144]可知，在多执行机构流体网络中考虑到没有全为树枝的回路，则 是一个满秩的矩阵。

反证法，假定 存在两行向量是等同的，则必存在一个全为树枝的回路，但这又与上述描述相违背；同样的，可以用反证法证明在 的列向量中也不存在其中一列为其他列的线性组合。

证毕

引理2.2 ：矩阵 E _Qc K _c S _Ha + K _a 的逆存在。

证明：

写出满足KVL的回路矩阵和满足KCL的割集矩阵的紧式。

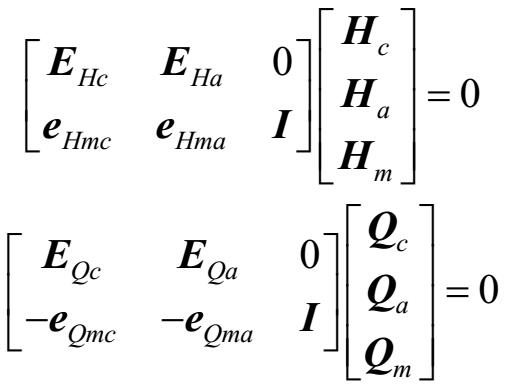
由参考文献[144]可知，回路矩阵和割集矩阵存在如下关系：

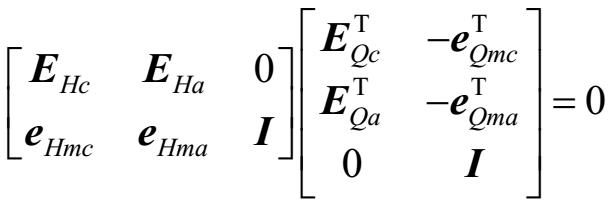
由式（2-43）可得：

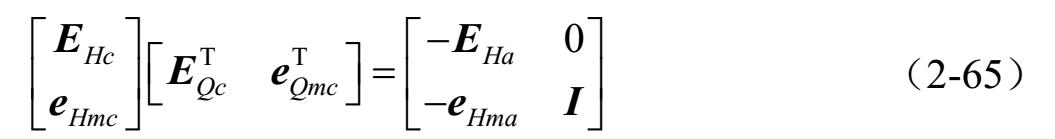
或

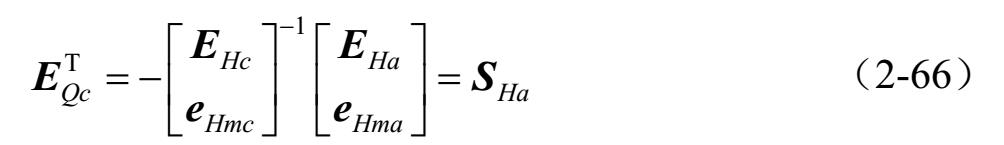
由式（2-43）可知， E _Q 是满秩的，所以 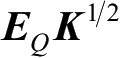可以由奇异值分解因式分解为 ^[145] ：

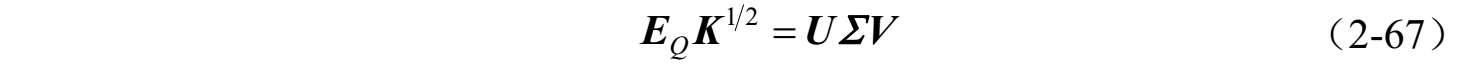
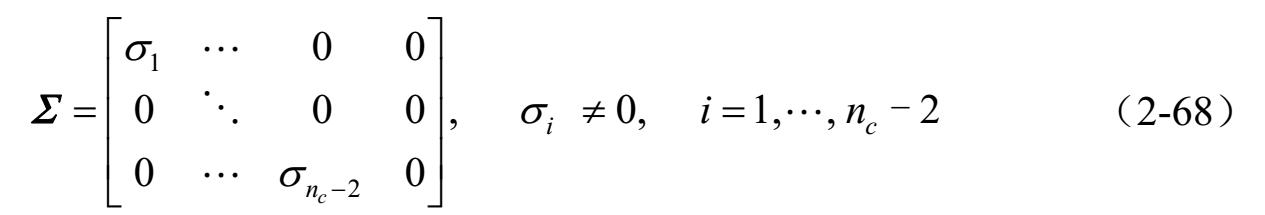
由式（2-67）和式（2-68）可得：

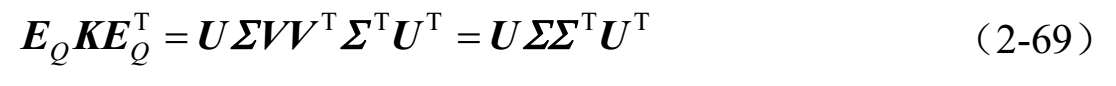
可得：

把式（2-37）、式（2-43）和式（2-66）代入式（2-70）得：

所以 E _Qc K _c S _Ha + K _a 的逆存在。

证毕

评注2.1 ：流体网络的全阶模型可以不用回路矩阵 E _H 和 e _Hm 表示。

由式（2-65）可得：

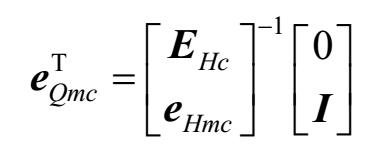
根据以上描述和式（2-66）可知，所有的辅助矩阵可以不用回路矩阵 E _H 和 e _Hm 表示，即： s5vvdwfaeTlAEDjHWYsIe/19m/W/wai9HrNf7pLlkBGIHTZFSKZrU/hkXJtI3mMC