





递归是一种特别有用的工具,不仅在数学中广泛应用,在日常生活中也常常遇到。例如一个画家所制作的如图1-21所示的一幅画便是一种递归的图形。
图1-21 递归图形
递归是设计和描述算法的一种有力的工具,由于它在复杂算法的描述中被经常采用,能采用递归描述的算法通常有这样的特征:为求解规模为N的问题,设法将它分解成规模较小的问题,然后从这些小问题的解中方便地构造出大问题的解,并且这些规模较小的问题也能采用同样的分解和综合方法,分解成规模更小的问题,并从这些更小问题的解中构造出规模较大问题的解。特别地,当规模N=1时,能直接得解。
递归算法包括“递推”和“回归”两部分。递推就是为得到问题的解,将它推到比原问题简单的问题的求解。如f(n)=n!,为计算f(n),将它推到f(n-1),即f(n)=nf(n-1),这就是说,为计算f(n),将问题推到计算f(n–1),而计算f(n–1)比计算f(n)简单,因为f(n–1)比f(n)更接近于已知解0!=1。使用递推时应注意:
(1)递推有终止的条件。所谓“终止条件”就是在此条件下问题的解是明确的,缺少终止条件便会使算法失效。例如n!,当n=0时,0!=1为递推的终止条件。
(2)“简单问题”表示离递推终止条件更为接近的问题。简单问题与原问题解的算法是一致的,其差别主要反映在参数上。例如,f(n–1)与f(n)其参数相差1。参数变化,使问题递推到有明确解的问题。
回归是指当“简单问题”得到解后,回归到原问题的解上来。例如,当计算完f(n–1)后,回归计算nf(n–1),即得n!的值。使用回归应注意:
(1)递归到原问题的解时,算法中所涉及的处理对象应是关于当前问题的,即递归算法所涉及的参数与局部处理对象是有层次的。当解一问题时,有它的一套参数与局部处理对象。当递推进入一“简单问题”时,这套参数与局部对象便隐蔽起来,在解“简单问题”时,又有它自己的一套。但当回归时,原问题的一套参数与局部处理对象又活跃起来了。
(2)回归到原问题以得到问题的解,回归并不引起其他操作,如下例所示。
计算n!。
其公式为:
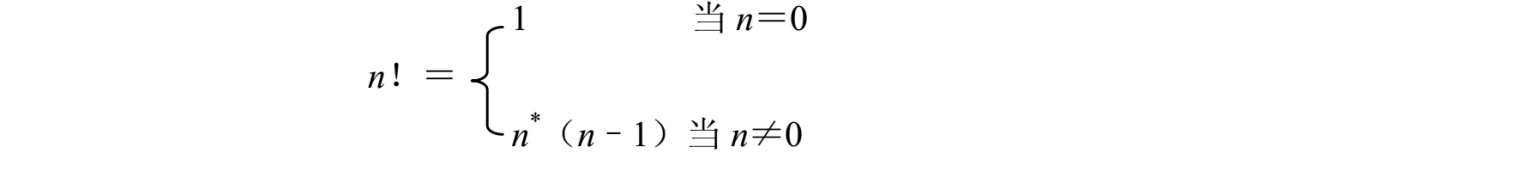
程序片段如下:
【程序1-1】

图的深度优先搜索、二叉树的前序、中序和后序遍历等可采用递归实现。
问题描述 :编写计算斐波纳契(Fibonacci)数列,数列大小为n。
无穷数列1,1,2,3,5,8,13,21,35,…称为斐波纳契数列,其递归定义如下:

由斐波纳契数列的递归定义可知,当n大于1时,这个数列第n项的数值是它前面两项之和。由于递归算法的执行过程分递推和回归两个阶段,在递推阶段,程序把较复杂的问题(规模为n)的求解推到比原问题简单一些的问题(规模小于n)的求解,在回归阶段,程序由在规模很小时求得的解得到较复杂问题的解。因此,对于斐波纳契数列的求解,要得到数列第n项的值,就必须求得数列第n–1项的值。同理,要求得数列第n–1项的值,就必须求得数列第n–2项的值,依次递推下去,最后需要求得数列第1项和第0项的值,递推部分结束。又当n等于0和1时,其数值为1,根据这些值可求出数列第2项的值,再根据数列第2项的值可得到第3项的值,依次回归,最后可依次得到数列第n–2、n–1和n项的值。由这个例子,我们可以很清楚地了解递归的形式和过程。该问题程序实现如下:
【程序1-2】


问题描述: 本程序将一段以*结束的文本中的单词按字典中的顺序打印出来,并且打印出该单词在正文中的出现次数。
考虑到二叉排序树可以很容易地递归实现,我们使用二叉排序树来实现文本中单词按字典顺序排序。程序中使用二叉排序树存入单词,即每次从文件中读出一个单词,都将其按单词的字典顺序存入一个二叉排序树,第一个存入的单词为二叉排序树的根。读完文件中的单词后,中序遍历打印出二叉排序树中存放的各个单词。
为了使存储空间使用更加合理且能够处理任意长度的单词,程序设立了一个数组text,所有读入的单词都放在 text 数组中。函数getword 完成读入单词的操作,并返回所读入单词的长度。函数insert 完成在二叉排序树中插入一个新结点的操作并返回指向二叉树根结点的指针。
该问题算法程序实现如下:
【程序1-3】


本程序由4部分组成,3个子程序和一个主程序。子程序getword用来输入单词;子程序insert用来将单词插入到中序排序二叉树中;子程序print_tree用来中序遍历二叉排序树并打印。单词存放在数组text中,且单词和单词之间用字符‘0’分开。初始时数组word和text的首地址相等。