1.2　十六进制计数法

1.2.1　十六进制计数法的原理

二进制数和计算机电路有着近乎直观的联系。电路的状态，可以用二进制数来直观地描述，而一个二进制数，也容易使我们仿佛观察到了每根电线上的电平变化。所以，我们才形象地说，二进制是计算机的官方语言。

即使是在平时的学习和研究中，使用二进制也是必需的。一个数字电路输入什么，输出什么，电路的状态变了，是哪一位发生了变化，研究这些，肯定要精确到每一个比特。这个时候，采用二进制是最直观的。

但是，二进制也有它的缺点。眼下看来，它最主要的缺点就是写起来太长，一点也不方便。为此，人们发明了十六进制计数法。至于为什么要发明另外一套计数方法，而不是依旧采用我们熟悉的十进制，下面就要为大家解释。

一旦知道二进制有两个数符“0”和“1”，十进制有十个数符“0”到“9”，那么我们就会很自然地认为十六进制一定有16 个数符。

一点没错，完全正确。这16 个数符分别是0、1、2、3、4、5、6、7、8、9、A、B、C、D、E、F。

你可能会觉得惊讶，字母怎么可以当做数字来用？这样的话，那些熟悉的英语单词，像Face（脸）、Bad（坏的）、Bed（床）就都成了数。

这又有什么奇怪的？你觉得“0”、“5”、“9”是数字，而“A”、“B”不是数字，这是因为你已经从小习惯了这种做法。

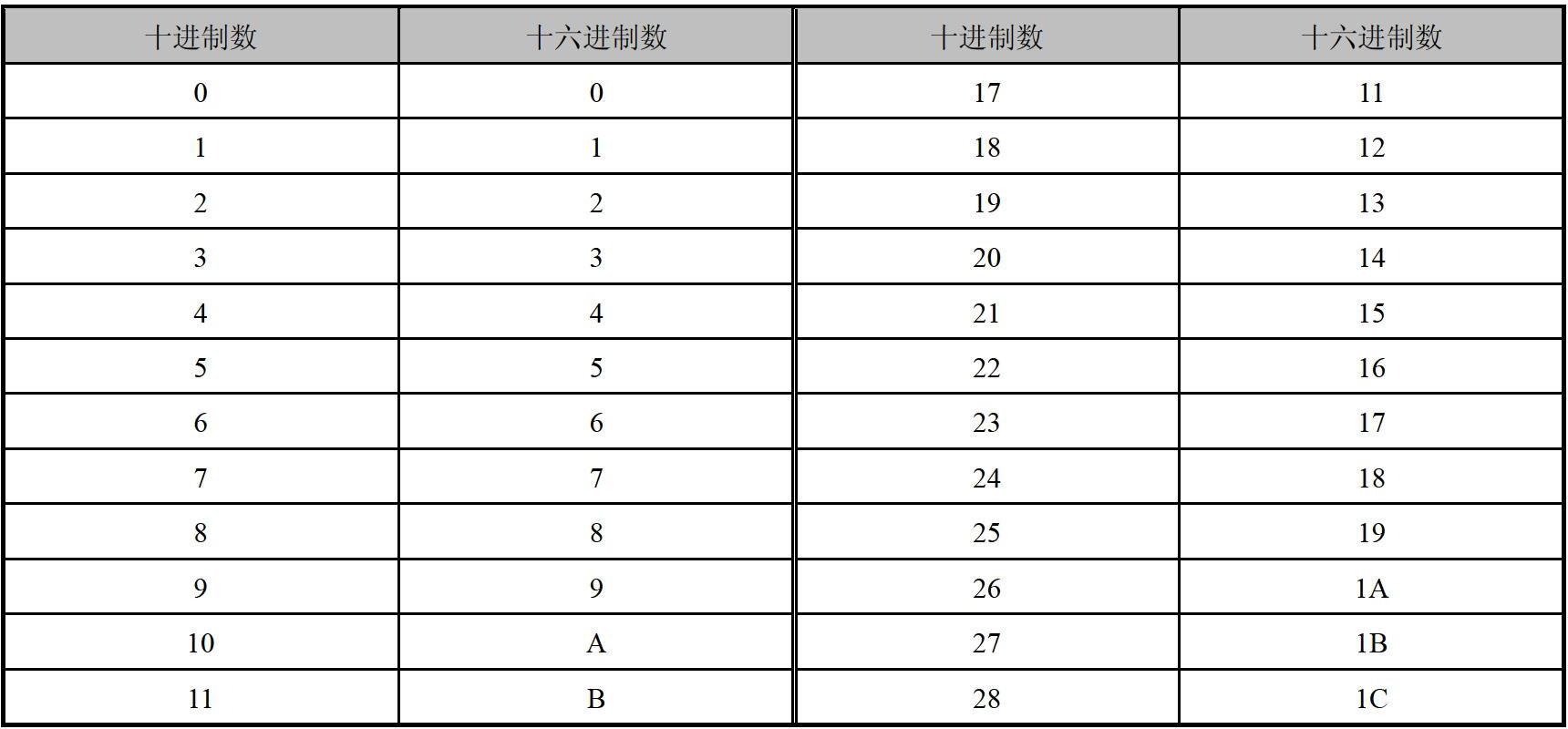
对于自然数里的前10 个，十进制和十六进制的表示方法是一致的。但是，9 之后的数，两者的表示方法就大相径庭了，如表1-1 所示。

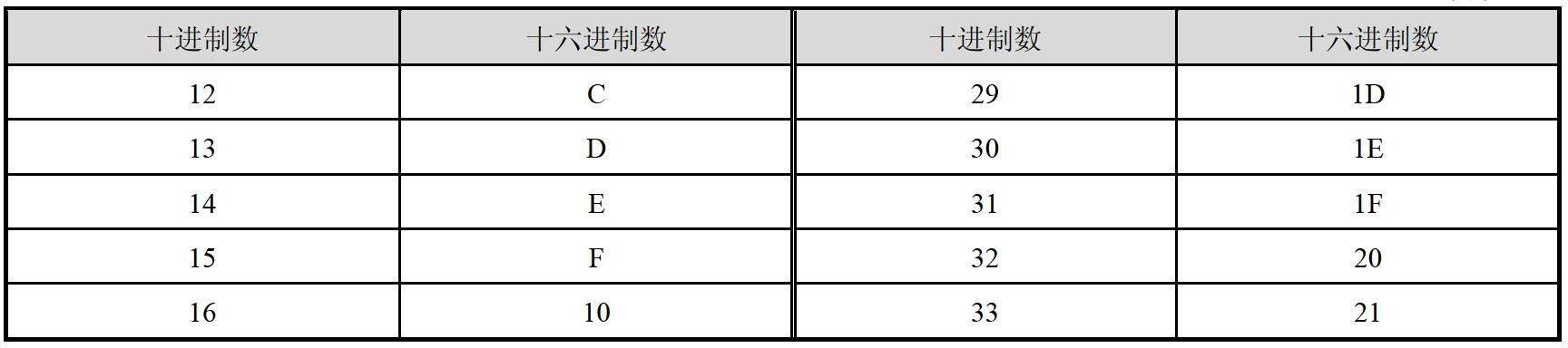
很显然，一旦某个数位增加到9 之后，下一次，它将变成A，而不是向前进位，因为这里是逢16 才进位的。进位只发生在某个数位原先是F 的情况下，比如1F，它加一后将会变成20。

1.2.2　十六进制到十进制的转换

要把一个十六进制数转换成我们熟悉的十进制数，可以采用和前面一样的方法。只不过，计算各个数位的权时，幂的底数是16。比如将十六进制数125 转换成十进制数的方法如下：

125H＝1×16 ² ＋2×16 ¹ ＋5×16 ⁰ ＝293D

上式里，125 后面的“H”用于表明这是一个十六进制数，它是英语单词Hexadecimal 的头一个字母，这个单词的意思是十六进制。

检测点1.3

将下列十六进制数转换成十进制数：

8、A、B、C、D、E、F、10、1F、6CD、3FE、FFC、FFFF

1.2.3　十进制到十六进制的转换

如图1-3 所示，相应地，要把一个十进制数转换成十六进制数，则可以采取不停地除以16 并取其余数的策略。

第1 次，将293 除以16，商为18，余5；

第2 次，用18 除以16，商为1，余2；

第3 次，再用1 除以16，商为0，余1，结束。

然后，从下往上，将每次的余数1、2、5 列出来，得到125，这就是所要的结果。

检测点1.4

将下列十进制数转换成十六进制数：

8、10、12、15、25、64、100、255、1000、65535、1048576

1.2.4　为什么需要十六进制

为什么我们要发明十六进制计数法？为什么我们要学习它？

提出这样的问题，在我看来很有趣，也很有意义，但似乎从来没有人在书上正面回答过。这样一来，可怜的学子们只能在掌握了十六进制若干年之后，在某一天里自己恍然大悟。

为了搞清楚这个问题，我们不妨来列张表（表1-2），看看十进制数、二进制数和十六进制数之间，都有些什么有趣的规律和特点。

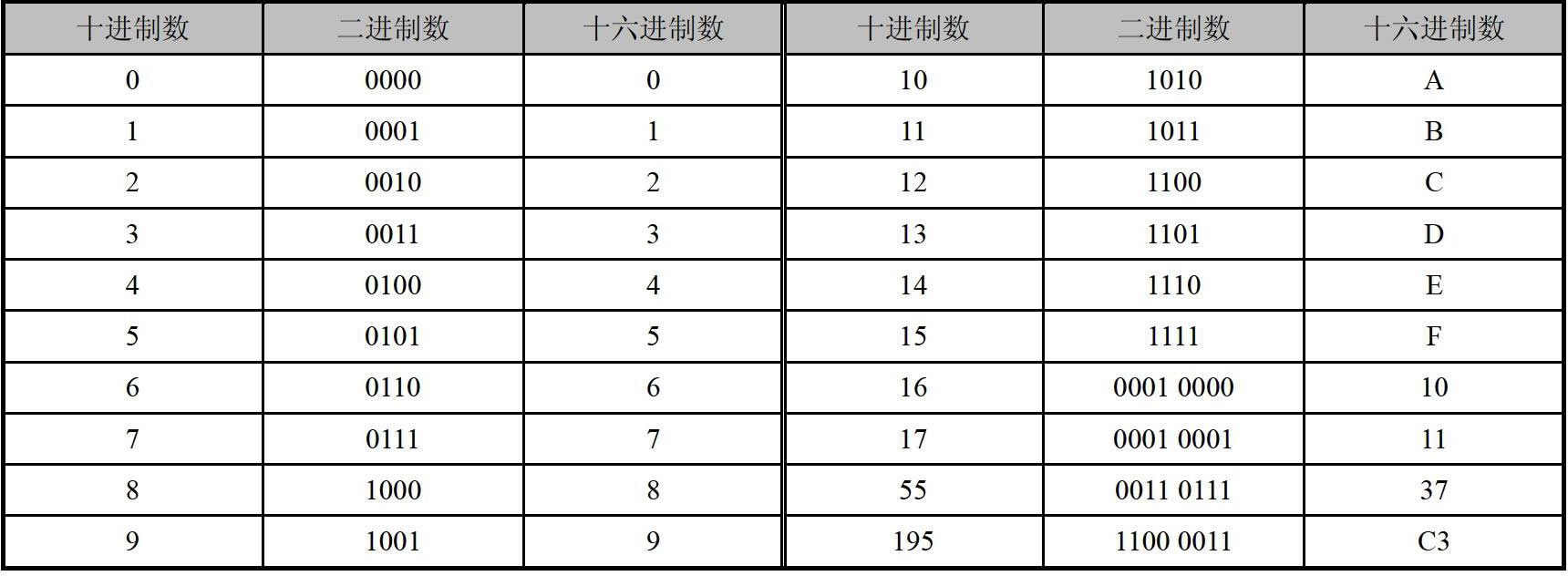
在上面这张表里（表1-2），每一个二进制数在排版的时候，都经过了“艺术加工”，全都以4比特为一组的形式出现。不足4 比特的，前面都额外加了“0”，比如10，被写成0010 的形式。就像十进制数一样，在一个二进制数的前面加多少个零，都不会改变它的值。

注意观察这张表并开动脑子，4 比特的二进制数，可以表示的数是0000 到1111，也就是十进制的0～15，这正好对应于十六进制的0～F。

在这个时候，如果将它们都各自加1，那么，下一个二进制数是0001 0000，与此同时，它对应的十六进制数则是10，你会发现，它们有着如图1-4（左边）所示的奇妙对应关系。

再比如图1-4（右边）中的二进制数1100 0011，它与等值的十六进制数C3 也有着相同的对应关系。

也就是说，如果将一个二进制数从右往左，分成4 比特为一组的形式，分别将每一组的值转换成十六进制数，就可以得到这个二进制数所对应的十六进制数。

这样一来，如果我们稍加努力，将0～F 这16 个数所对应的二进制数背熟，并能换算自如的话，那么，当我们看到一个十六进制数3F8 时，我们就知道，因为3 对应的二进制数为0011，F对应的二进制数是1111，8 对应的二进制数是1000，所以3F8H＝0011 1111 1000B。

同理，如果一个二进制数是1101 0010 0101 0001，那么，将它们按4 比特为一组，分别换算成十六进制数，就得到了D251。

正如前面所说的，从事计算机的学习和研究（包括咱们马上就要进行的汇编语言程序设计），不可避免地要与二进制数打交道，而且有时还必须针对其中某些比特进行特殊处理。这个时候，如果想保留二进制数的直观性，同时还要求写起来简短，十六进制数是最好的选择。

检测点1.5

1．将下列十六进制数转换成二进制数：

3、A、C、F、20、3F、2FE、FFFF、9FC05D、7CCFFEFF

2．快速说出以下十进制数所对应的二进制数和十六进制数：

1、3、5、7、9、11、13、15、0、2、4、6、8、10、12、14 A4cR5EB/pOu8gLY3YIQbK4wlESGQVllMVhU/Mt6f5LM5aAAb+xgZPKJrt2b91G3J