




 1.1 二进制计数法回顾
1.1 二进制计数法回顾
在《穿越计算机的迷雾》那本书里我们已经知道,计算机也是一台机器,唯一不同的地方在于它能计算数学题,且具有逻辑判断能力。
与此同时,我们也已经在那本书里学到,机器在做数学题的时候,也面临着一个如何表示数字的问题,比如你采用什么办法来将加数和被加数送到机器里。
同样是在那本书里,我们揭晓了答案,那就是用高、低两种电平的组合来表示数字。如图1-1所示,参与计算的数字通过电线送往计算机器,高电平被认为是“1”,低电平被认为是“0”,这样就形成了一个序列“11111010”,这就是一个二进制数,在数值上等于我们所熟知的二百五,换句话说,等于十进制数250。
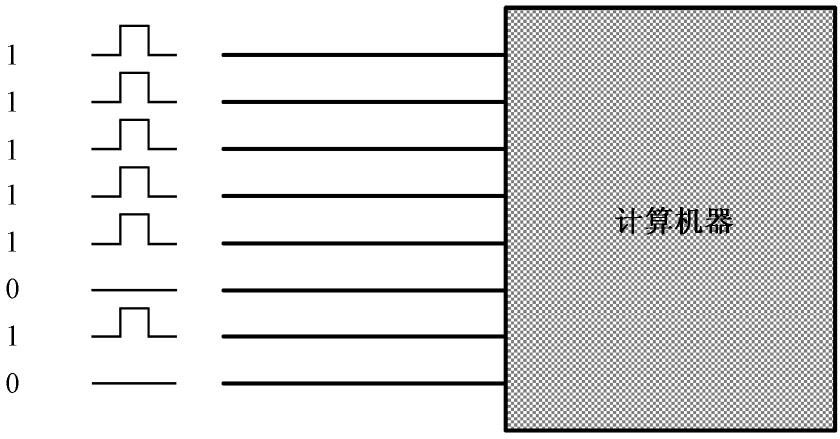
图1-1 在计算机里,二进制数字对应着高低电平的组合
从数学的角度来看,二进制计数法是现代主流计算机的基础。一方面,它简化了硬件设计,因为它只有两个符号“0”和“1”,要得到它们,可以用最少的电路元件来接通或者关断电路就行了;另一方面,二进制数与我们熟悉的十进制数之间有着一对一的关系,任何一个十进制数都对应着一个二进制数,不管它有多大。比如,十进制数5,它所对应的二进制数是101,而十进制数5785478965147则对应着一长串“0”和“1”的组合,即1010100001100001001011010110010011110011011。
组成二进制数的每一个数位,称为一个比特(bit),而一个二进制数也可以看成是一个比特串。很明显,它的数值越大,这个比特串就越长,这是二进制计数法不好的一面。
每一种计数法都有自己的符号(数符)。比如,十进制有0、1、2、3、4、5、6、7、8、9 这十个符号;二进制呢,则只有0、1 这两个符号。这些数字符号的个数称为基数。也就是说,十进制有10 个基数,而二进制只有两个。
二进制和十进制都是进位计数法。进位计数法的一个特点是,符号的值和它在这个数中所处的位置有关。比如十进制数356,数字6 处在个位上,所以是“6 个”;5 处在十位上,所以是“50”;3 处在百位上,所以是“300”。即:
百位3、十位5、个位6=3×10 2 +5×10 1 +6×10 0 =356
这就是说,由于所处的位置不同,每个数位都有一个不同的放大倍数,这称为“权”。每个数位的权是这样计算的(这里仅讨论整数):从右往左开始,以基数为底,指数从0 开始递增的幂。正如上面的公式所清楚表明的那样,“6”在最右边,所以它的权是以10 为底,指数为0 的幂10 0 ;而3 呢,它的权则是以10 为底,指数为2 的幂10 2 。
上面的算式是把十进制数“翻译”成十进制数。从十进制数又算回到十进制数,这看起来有些可笑,注意这个公式是可以推广的,可以用它来将二进制数转换成十进制数。
比如一个二进制数10110001,它的基数是2,所以要这样来计算与它等值的十进制数:
10110001B=1×2 7 +0×2 6 +1×2 5 +1×2 4 +0×2 3 +0×2 2 +0×2 1 +1× 2 0=177D
在上面的公式里,10110001B 里的“B”表示这是一个二进制数,“D”则表示177 是个十进制数。“B”和“D”分别是英语单词Binary 和Decimal 的头一个字母,这两个单词分别表示二进位和十进位的意思。
检测点1.1
将下列二进制数转换成十进制数:
1101、1111、1001110、11111111、10000000、1101101100011011
为了将一个十进制数转换成二进制数,可以采用将它不停地除以二进制的基数2,直到商为0,然后将每一步得到的余数串起来即可。如图1-2 所示,如果要将十进制数26 转换成二进制数11010,那么可采用如下方法:

图1-2 将十进制数26 转换成二进制数
第1 步,将26 除以2,商为13,余数为0;
第2 步,用13 除以2,商为6,余数为1;
第3 步,用6 除以2,商为3,余数为0;
第4 步,用3 除以2,商为1,余数为1;
第5 步,用1 除以2,商为0,余数为1,结束。
然后,从下往上,将每一步得到的余数串起来,从左往右书写,就是我们所要转换的二进制数。
检测点1.2
将下列十进制数转换成二进制数:
8、10、12、15、25、64、100、255、1000、65535、1048576