




由A.A.Shabana提出的绝对节点坐标法可以说是柔性多体力学发展的一个重要进展,是近年来最具有代表性的多体动力学研究成果;它同时也是对有限元技术的较大拓展和创新。通常在有限元法中,梁单元、板壳单元由于采用节点微小转动作为节点坐标,因而不能精确描述刚体大变形运动。在绝对节点坐标法中,由于采用节点位移和节点斜率作为节点坐标,其形函数不仅可以有结构的弹性变形,而且能够描述任意刚体大变形位移。从而利用绝对节点坐标方程可以对作大变形柔性体的运动进行研究。同时,利用绝对节点坐标方程时,梁和板壳可以看作等参单元,这样系统的质量阵为一常数阵,然而,其刚度阵为强非线性阵。从理论上讲,绝对节点坐标方程是基于连续结构几何非线性理论,由于保留了纵向应变和弹性力的高阶项,所以,绝对节点坐标方程能够分析结构大变形,以及转动等运动及动力学问题,已经应用于多项工程的研究之中。
最近提出的有限元多柔性体MFBD(Multi-Flexible-Body Dynamics)技术是多体动力学发展的又一个重要成就。它首次实现了有限元技术与多体动力学的有机结合,克服了模态柔性体的缺点,能够精确表达接触力引起的局部变形,并且能够表达柔体累计的非线性变形,可用于结构大变形的分析,在分析的过程中,可以得到结构柔性体上节点应力随时间变化的过程。需要说明的是,MFBD 技术不是取代了模态缩减法,而是采用“节点法”对它进行了补充和扩展,应用到真实的有限元结构,从而可以在一个系统中合并两种方法。
与模态柔性体不同的是,有限元柔性体利用柔性体节点之间的相对位移和相对旋转作为描述柔性体变形的量。有限元多柔体技术是现代最新的多体动力学仿真技术,它在充分考虑系统动力学的前提下,对柔性体和复杂接触进行了一个正确的表述。首次将多体动力学分析和有限元分析两个单独的领域合并起来,排除了模态缩减的明显弊端。采用此方法,能够精确地预测柔性体之间,以及柔性体和刚体间的接触问题,同时能够直接得到有效的应力结果。“模态缩减”方法求解有限元结构问题,通过有限元程序预先求解结构的特征值,进而得到模态缩减的柔性体结构。该方法已经满足了许多应用的需要,但是对于一些重要的应用呈现出了较大局限性。一方面这些线性化的柔性体不允许出现大变形,更为重要的是不具备足够的刚度信息,接触计算比较困难,甚至不能实现。因为结果的好坏直接取决于从有限元程序倒入特征值,评价组件的应力显得非常重要。有限元柔性体新技术不是为了取代模态缩减法,而是采用“节点法”对它补充扩展,应用真实的有限元结构,在一个系统中合并两种方法。
采用有限元柔性体,不再需要一个单独的有限元工具预先对柔性体求解,仿真过程中通过反复计算结构矩阵,可以进行精确地应力分析、考虑柔性体结构间的碰撞与接触,以及考虑非线性变形。
以下以梁单元的有限元柔性体为例来说明有限元柔性体的建模原理。
如图 1-1 所示,系统是由按照一定次序连接而成的三维梁单元组成的多柔性体系统,在这个系统中将相邻节点的相对位移作为基本未知量,从而建立整个系统的运动方程。在空间结构中把已经离散化的连续的一系列梁单元中任意取出两个单元 i −1和 i (图 1-2)。单元 i −1由节点 i −1和 i 组成,单元 i 由节点 i 和节点 i +1组成。在空间结构中,在每个梁单元的节点上有 6 个自由度:沿着 X 、 Y 、 Z 三个方向的线位移和绕 X 、 Y 、 Z 三个轴的角位移。节点坐标的 X 轴方向为沿着梁单元的纵向的方向, Z 轴方向为沿着梁单元的横向方向, Y 轴方向由右手定则确定。变形前后的两个梁单元如图 1-2 所示。引入梁单元的节点参考坐标系,来描述节点的位置和方向矢量。图 1-2 中的坐标系 X - Y - Z 为总体惯性坐标系; x k − y k − z k ( k 为梁单元的节点编号 i , j )为节点 k 的节点参考坐标系; r k 表示节点 k 在总体惯性坐标系的位置矢量。 x ( i -1) i − y ( i -1) i − z ( i -1) i 为固结在节点 i 上,关于节点 i −1的为随体坐标系。随体坐标系与结构力学中有限元单元坐标系相同,是与节点上邻域的微元相固连的,而不是浮动的,即随体坐标系随着柔性体的变化而变化。在单元 i -1 没有变形的情况下,节点随体参考坐标系 x ( i -1) i − y ( i -1) i − z ( i -1) i 为固结在节点 i 和节点参考坐标系 x i -1 − y i -1 − z i -1 为固结在节点 i 的方向是一致的。
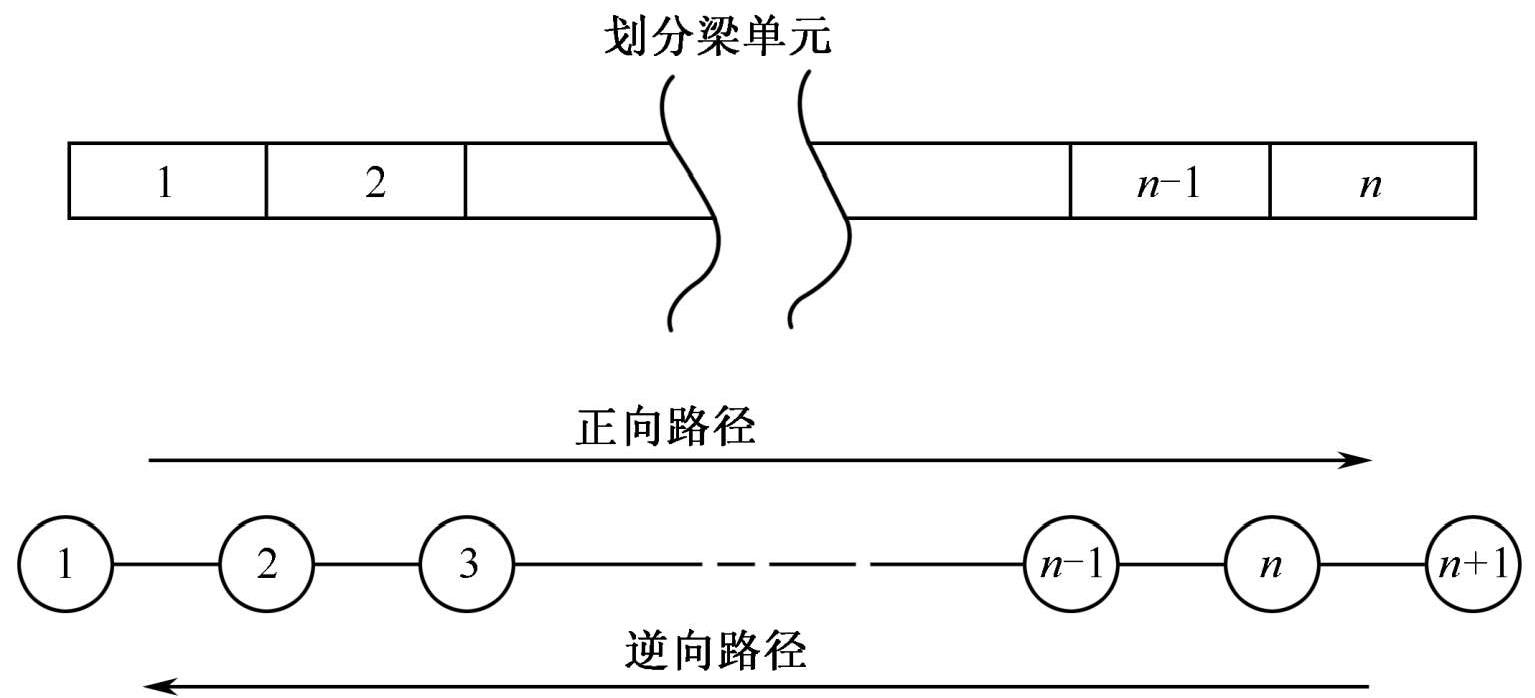
图 1-1 梁单元划分及节点分布
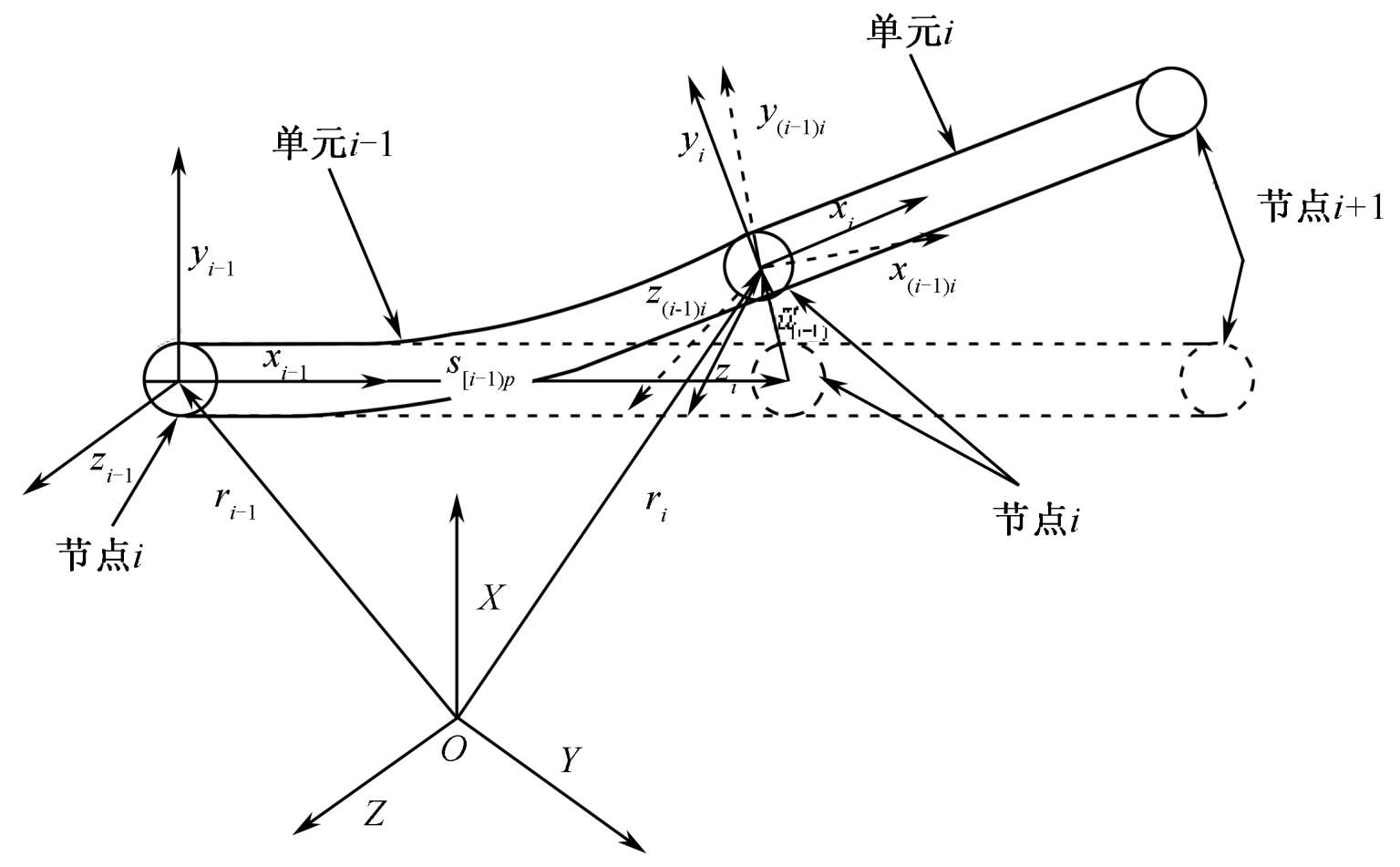
图 1-2 梁单元变形示意图
对于柔性体任意一点 p 的位置变化可以表示为

式中, r 为点 p 在总体惯性坐标系中关于 X 、 Y 、 Z 的位置矢量; r o 为浮动坐标系原点在总体惯性坐标系中的位置矢量; A 为关于空间坐标变换的方向余弦矩阵; s p 为柔性体在没变形时,点 p 在随体坐标系中位置矢量; u p 为相对变形矢量,包括位置变形及方向的变化。
系统任意一节点在惯性坐标系的速度和虚位移分别定义为

节点相对的速度和虚位移定义为


在式(1-29)及式(1-30)中,矩阵 A 为节点坐标系到惯性坐标系的方位转换矩阵。
节点 i 在惯性坐标系 X - Y - Z 的中的位置矢量分用节点 i −1的位置矢量,以及与节点 i −1相对变形表示为
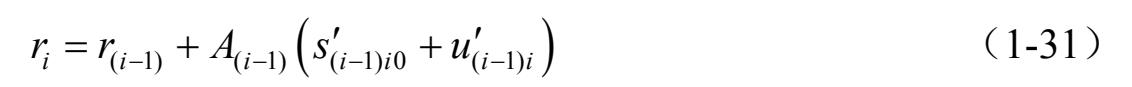
转换矩阵 A i 同 A i − 1 的关系可以表示为

相对角速度 ω i 同 ω i − 1 的可以表示为
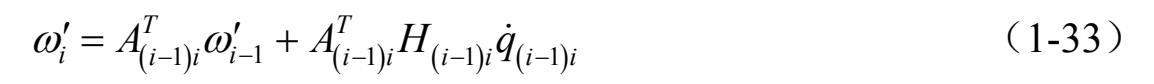
以上公式中,
A
k
(
k
=
i
,
i
−1 )表示节点
k
的参考坐标系相对于惯性坐标系的转换矩阵;
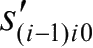 表示梁未变形时,相对坐标系
x
(
i
-1)
i
−
y
(
i
-1)
i
−
z
(
i
-1)
i
的位置矢量;
表示梁未变形时,相对坐标系
x
(
i
-1)
i
−
y
(
i
-1)
i
−
z
(
i
-1)
i
的位置矢量;
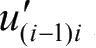 表示节点
i
相对于节点
i
−1的坐标系的变形矢量;矩阵
D
(
i
−
1)
i
表示由于节点坐标系
x
(
i
-1)
i
−
y
(
i
-1)
i
−
z
(
i
-1)
i
相对于节点
i
−1的转动而形成的转动转换矩阵;
C
(
i
−
1)
i
表示坐标系
x
i
−
y
i
−
z
i
相对于坐标系
x
(
i
-1)
i
−
y
(
i
-1)
i
−
z
(
i
-1)
i
转换的常矩阵。
表示节点
i
相对于节点
i
−1的坐标系的变形矢量;矩阵
D
(
i
−
1)
i
表示由于节点坐标系
x
(
i
-1)
i
−
y
(
i
-1)
i
−
z
(
i
-1)
i
相对于节点
i
−1的转动而形成的转动转换矩阵;
C
(
i
−
1)
i
表示坐标系
x
i
−
y
i
−
z
i
相对于坐标系
x
(
i
-1)
i
−
y
(
i
-1)
i
−
z
(
i
-1)
i
转换的常矩阵。
参考坐标系
x
i
-1
−
y
i
-1
−
z
i
-1
可通过3次旋转到达节点坐标系
x
i
-1
−
y
i
-1
−
z
i
-1
的坐标轴位置。在工程中经常使用经典欧拉转动顺序的主要是“3-1-3”旋转和“1-2-3”旋转。采用的“1-2-3”旋转顺序。在依次旋转的三个角坐标分别记为
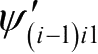 、
、
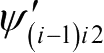 、
、
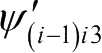 ,方位相对变化矢量写成矩阵的形式,即
,方位相对变化矢量写成矩阵的形式,即
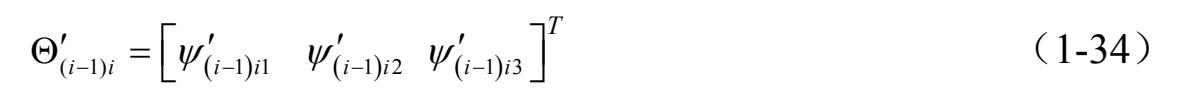
相应的变换矩阵 D ( i − 1) i 为三个转换矩阵的乘积,即
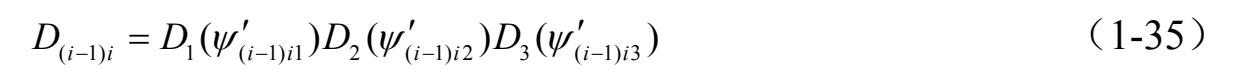
式中,
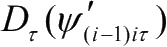 表示参考坐标系
表示参考坐标系
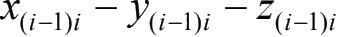 作
作
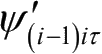 (
τ
=1,2,3)角度旋转时的变换矩阵。
(
τ
=1,2,3)角度旋转时的变换矩阵。
根据三维刚体系统动力学可知
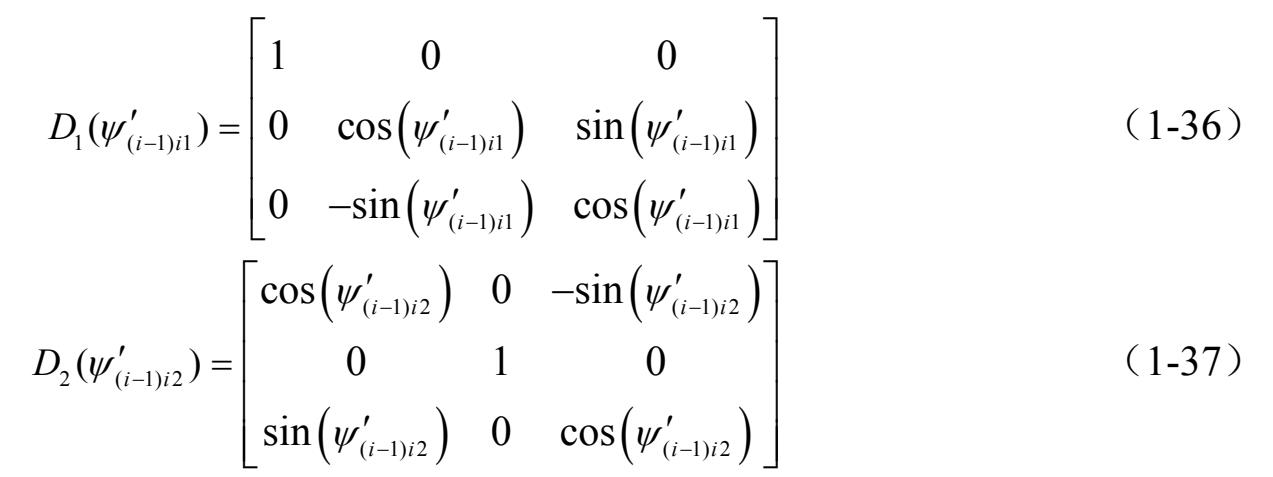
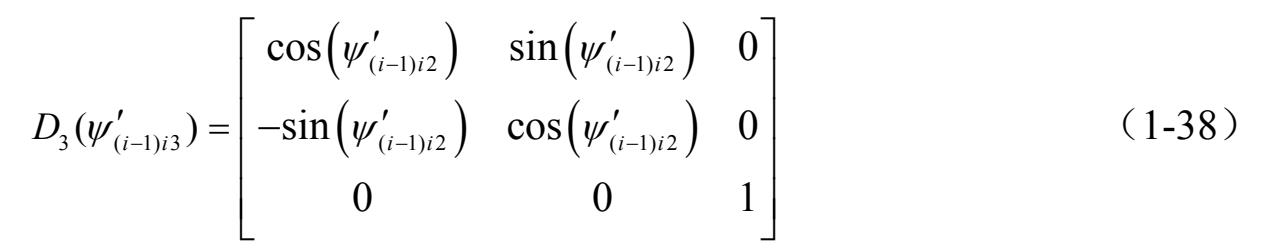
得到
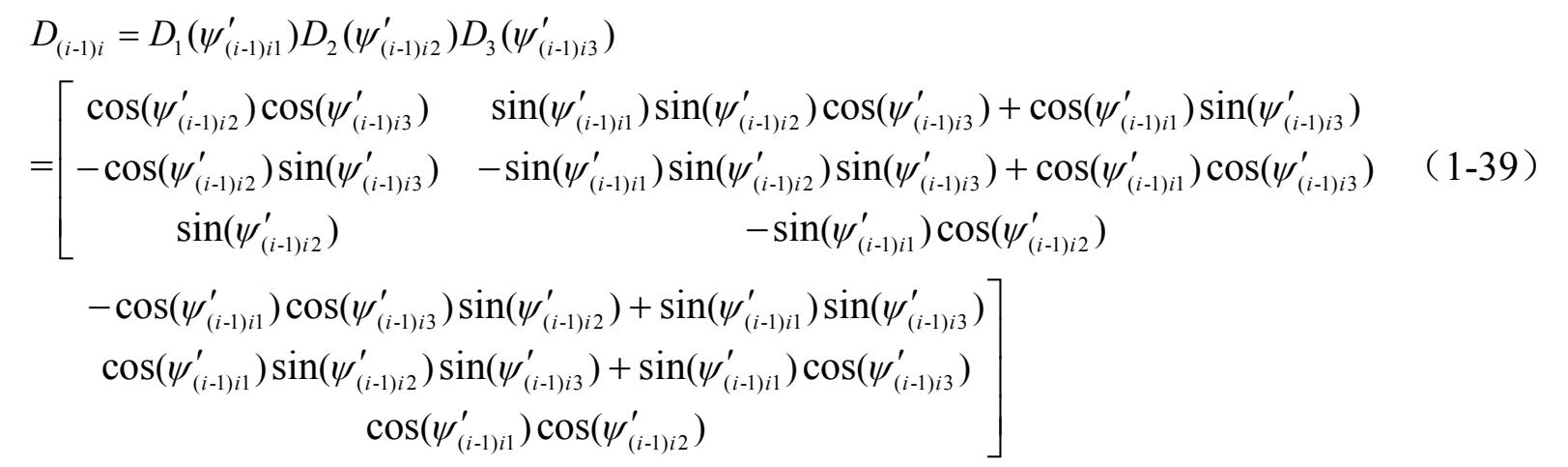
利用虚位移原理,对式(1-31)取变分得
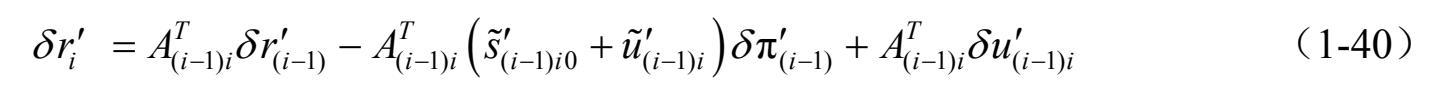
式(1-40)给出了虚位移
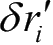 与
与
 的变换关系,式中,
的变换关系,式中,
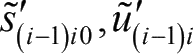 分别表示矩阵
分别表示矩阵
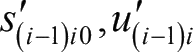 相应的的斜对称矩阵(或者称为反对称方阵)。
相应的的斜对称矩阵(或者称为反对称方阵)。
变换矩阵 A ( i − 1) i 、 A ( i − 1) 、 A i 的相互关系可以表示为

得

将式(1-42)带入式(1-41)中得
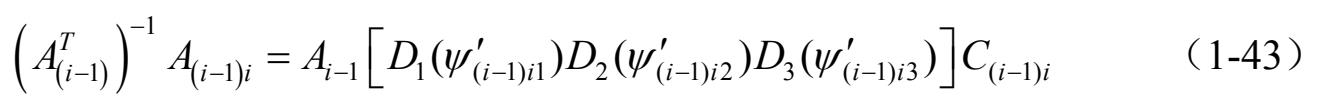
节点 i −1和节点 i 的相对旋转虚位移用 δ π i ′可以表示为
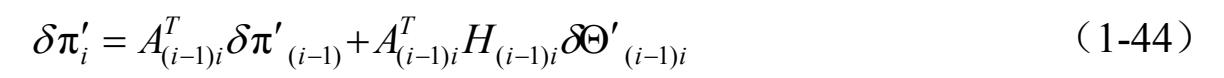
式(1-44)给出了旋转虚位移 δ π' i 和 δ π' i −1 之间的变换关系,即
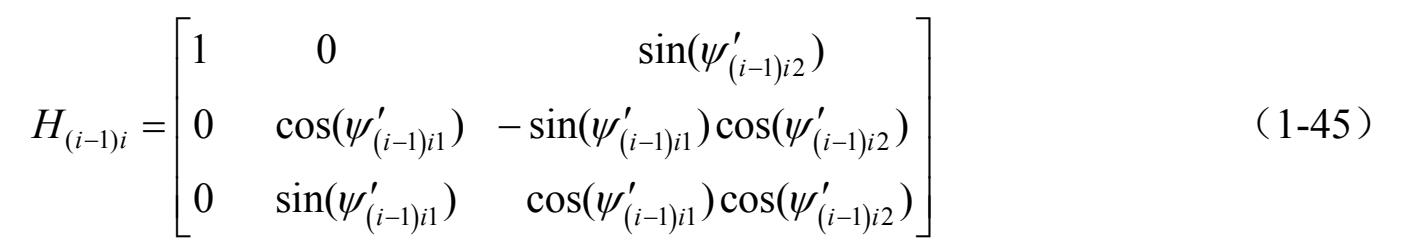
式(1-40)和式(1-44)联立,整理后写成矩阵的形式,即
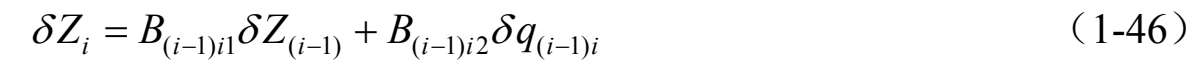
式(1-46)给出了两个相邻单元之间,节点虚位移的递推关系。这样沿着设定的路径顺序,反复利用式(1-46)就可以得到整个系统的节点之间的相对虚位移关系,可表示为

在式(1-47)中,
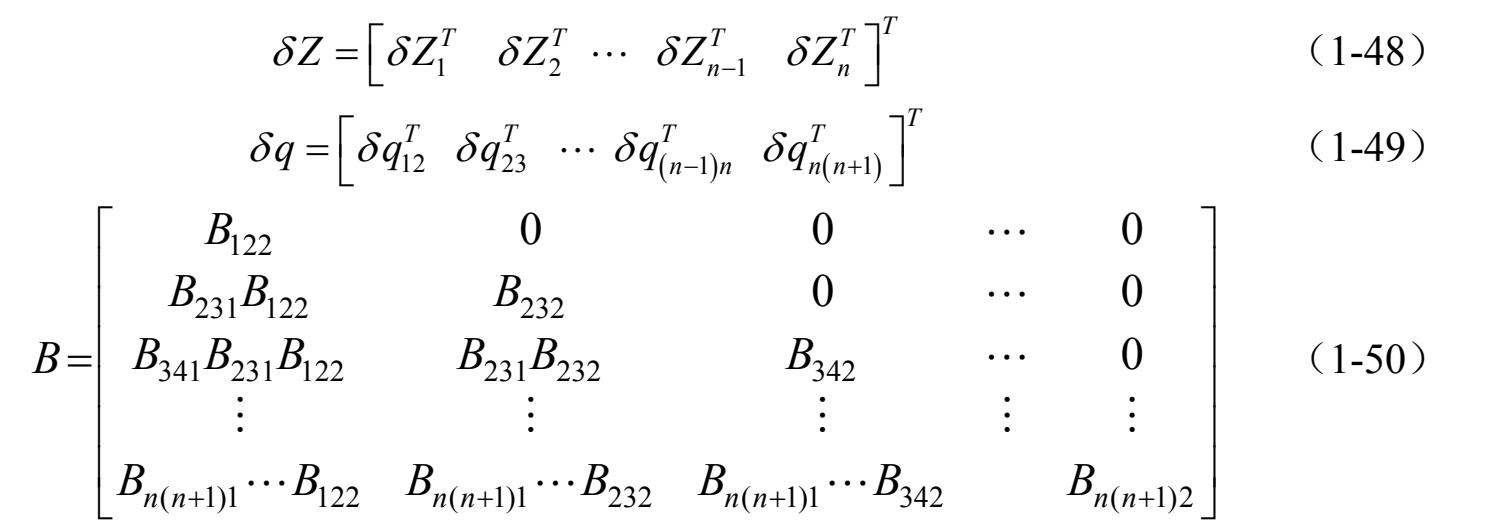
在以上诸式中,
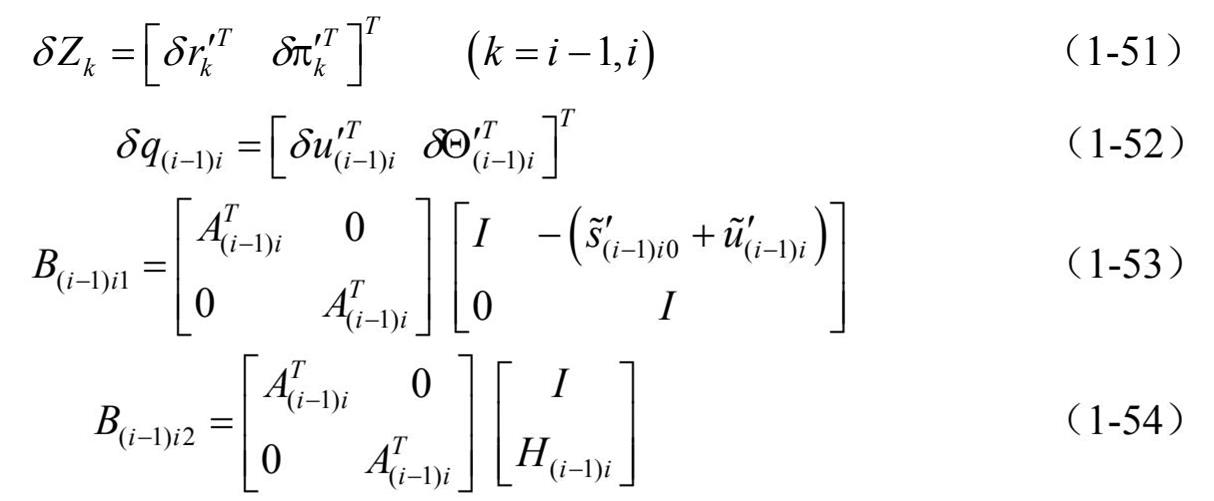
对式(1-31)、式(1-33)求导,联立得到
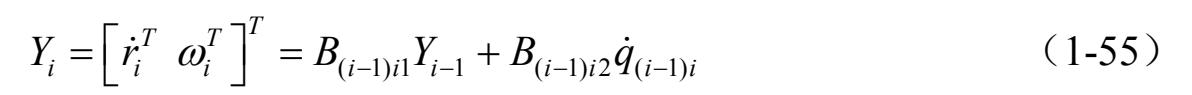
由式(1-55)可以得到系统在惯性坐标系下的节点速度同相对速度的关系,即

式中,
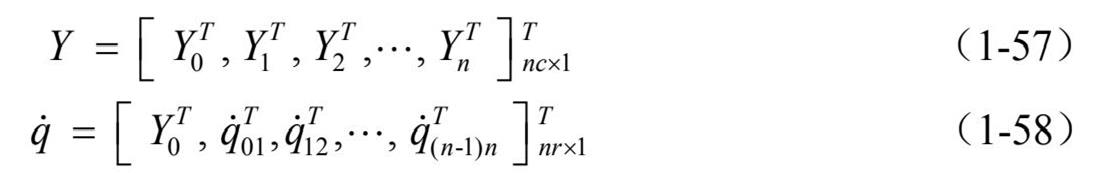
式中, nc 和 nr 分别表示惯性坐标系、相对坐标系中矢量的维数。
对式(1-55)求导,得到节点的加速度为
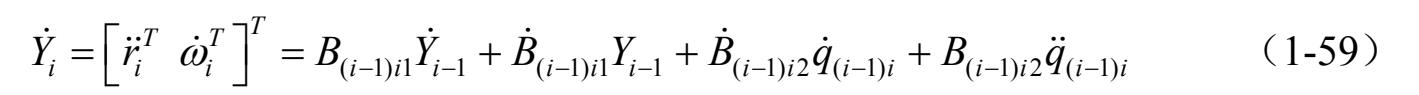
单元 i −1在相对节点坐标下的应变能写成虚功的形式表示为
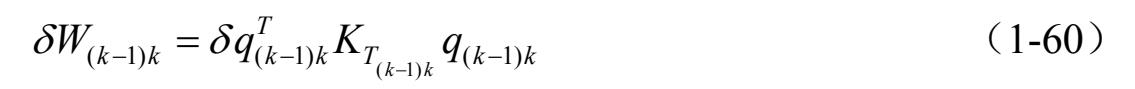
式中,
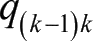 表示由节点
k
−1 与
k
相对位移,
表示由节点
k
−1 与
k
相对位移,
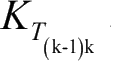 表示由节点
k
−1 与
k
组成的梁单元
k
−1的切线刚度矩阵。
表示由节点
k
−1 与
k
组成的梁单元
k
−1的切线刚度矩阵。
系统的应变能可以表示为
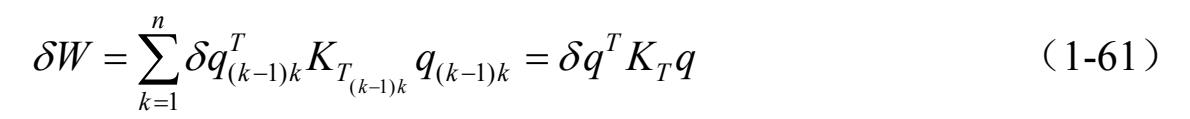
系统运动方程在惯性坐标系下的基本方程,又称为Euler-Lagrange 方程,可以写成下面微分代数方程的形式,即
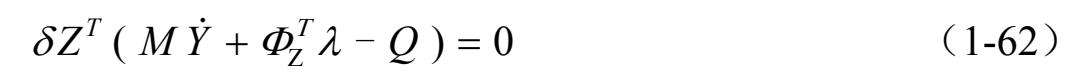
式中, Φ 表示约束矩阵; λ 为拉格朗日乘子。
将 δ Z = B δ q 带入式(1-62)得到
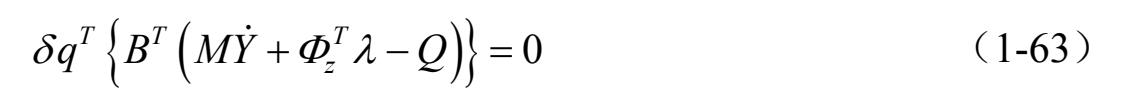
由于 δ q 是任意的,从而得到系统的动力学方程为
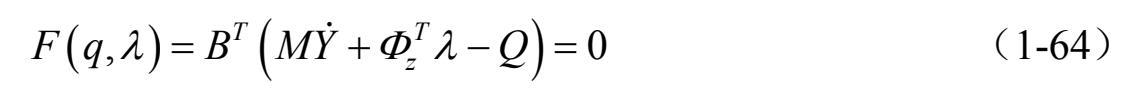
由以上的描述可知:有限元多柔性体技术由于采用节点之间的相对位移和旋转作为节点坐标来描述结构的变形,具有较高的计算精度,但是由于大大地增加了系统的求解规模,求解效率相对不高,这使得有限元柔性体的使用受到一定的限制,因而更多地应用于非线性大变形的分析;与之相反,模态柔性体由于缩减系统的求解规模,提高了计算的效率,但是模态柔性体的特性决定了它只能够应用于相对变形不大的结构分析中。