




进制换算就是数值在不同的计数制之间进行的等值或等价换算,数值在换算前后保持不变,只是表达方式不同而已。计数制是为不同的计数单位制定的标准。
通常,在我们日常生活中最习惯应用的是十进制,但实际应用中也会使用其他计数制,例如,十二进制(一打鸡蛋为十二个),六十进制(60 秒为一分钟,60 分钟为一小时)等,这种逢几进一的机制称为进位计数制。与C语言关系最密切的几种计数制是二进制、八进制、十进制和十六进制。
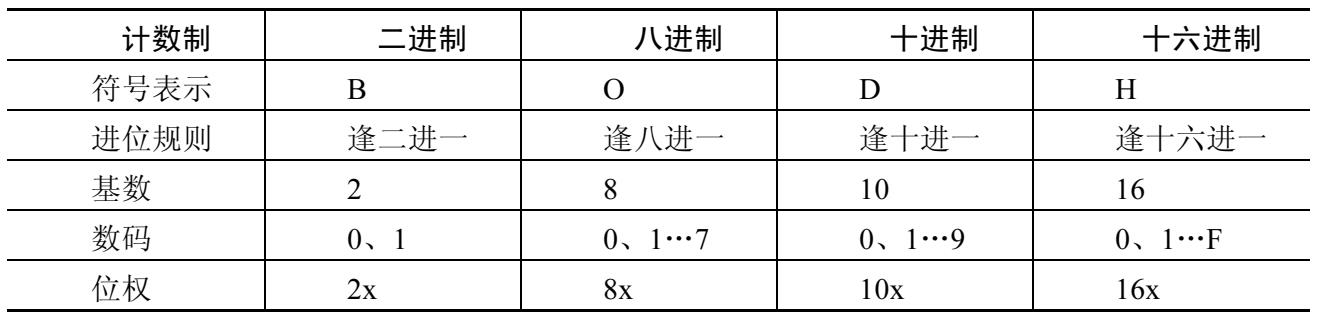
二进制是只使用 0 和 1 的计数制,采用逢二进一的进位方式。由于可以使用 0 和 1 分别代表电路中的高电平和低电平,因此现代电子计算机数据存储机制大都采用二进制。由于二进制不易读写和计算,因此产生了八进制和十六进制计数制。八进制共有 0、1、2、3、4、5、6、7 八个数,采用逢八进一的进位方式。十六进制共有 0、1、2、3、4、5、6、7、8、9、A、B、C、D、E、F十六个数,采用逢十六进一的进位方式。十六进制中字母部分不区分大小写,从A到F分别代表十进制数 10、11、12、13、14、15。另外还有日常生活中最常用的十进制,共有 0、1、2、3、4、5、6、7、8、9 十个数,采用逢十进一的进位方式。如表 2-1 所示为几种进制的基本规则,其中基数、数码和位权的概念在下节讲解中做详细描述。
表 2-1 几种进制基本规则
二进制数是由 0 和 1 组成的数字,下面介绍如何表示和计算二进制以及与其他进制的关系。
1. 二进制转换十进制
二进制转换为十进制分成两部分进行,一部分是整数部分,另一部分是小数部分,转换方法如范例 2.1 所示。
范例2.1 :将二进制数10010.11 (2) 转换为十进制数
解析:通常将二进制数做这样的换算
算式中下标(2)和(10)称做基数,同时也是计数单位;2 x 称做位权;0 和 1 称做数码。计算时幂指数可由右向左按数码位置从 0 算起,如右边最低位数码 1 对应的位权幂指数为 0,由此我们计算得二进制数 10010.11 (2) 相当于十进制数 18.75 (10) 。
2. 二进制转换八进制
二进制到八进制的转换采用三位一体的计算方法,同样分为整数和小数两部分考虑。如下示例:
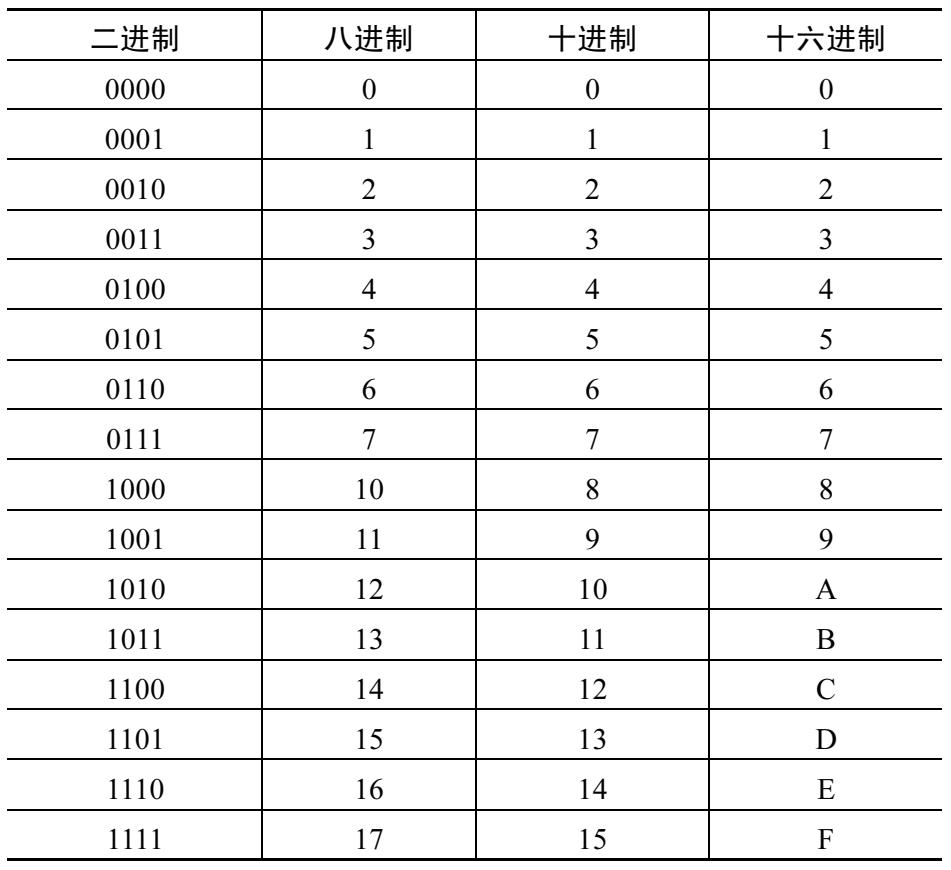
二进制到八进制的转换方法为将二进制数整数部分从右到左(小数部分从左到右),按每三位划分为一组,最左边(右边)不够三位的补 0。如上述算式中 100111.01101—〉100/111/011/010,将每组对应的八进制数代替二进制数,得到 4/7/3/2,去掉分隔符,得到八进制数 47.32。二进制与八进制的对应关系请查阅表 2-2 所示,二进制栏粗体部分表示对应八进制时的数组合。
范例2.2 :将二进制数1110100.101101 (2) 转换为八进制数
解析:按照三位一体的方法,将二进制数从右到左每三位划分为一组。查表 2-2 所示,将各组改为对应的八进制数,得到八进制数的结果。
计算流程如下:
3. 二进制转换十六进制
二进制到十六进制的转换采用四位一体的计算方法,计算时同样整数部分与小数部分分开,如下示例:
和二进制到八进制的转换方法类似,二进制到十六进制的转换方法为将二进制数整数部分从右到左(小数部分从左到右)按每四位划分为一组,最左(右)边不够四位的补 0。如上述算式中 100111.01101—〉0010/0111/0110/1000,将每组对应的十六进制数代替二进制数,得到 2/7/6/8,去掉分隔符,得到十六进制数 27.68。二进制与十六进制的对应关系请查阅表2-2 所示。
范例2.3 :将二进制数1110100.101101 (2) 转换为十六进制数
解析:按照四位一体的方法,将二进制数从右到左每四位划分为一组。查表 2-2 所示,将各组改为对应的十六进制数,得到十六进制数的结果。
计算流程如下:
表 2-2 进制转换表
八进制数由 0、1、2、3、4、5、6、7 这八个数组成,与二进制到其他进制的转换类似,八进制向其他进制的转换也有一定的规则,本书只讨论整数形式的八进制向其他进制的转换。
1. 八进制转换为十进制
八进制向十进制的转换也要按照位权和数码相乘再依次相加的方法。例如,下面的数制转换等式:
与二进制到十进制的转换类似,上式中八进制数 1270 到十进制的转换计算公式为:
算式中下标(8)和(10)称做基数,同时也是计数单位;8 x 称做位权;0、1、2 和 7 称做数码。计算时幂指数可自右向左按数码位置从 0 算起。如右边最低位数码 7 对应的位权幂指数为 0。由此我们计算得八进制数 1270 相当于十进制数 696。
2. 八进制转换为二进制
八进制数向二进制数的转换可以看做是二进制到八进制的逆运算。八进制到二进制的转换方法为将八进制数从右到左每位数字转换为 3 位二进制数,转换方法请参看表 2-2 所示,并去掉最左边的 0 位。
范例2.4 :将八进制数5361 (8) 转换为二进制数
解析:将八进指数从右到左依次转换为二进制数,计算方法为
注意:转换时每位八进制数字一定写满 3 位数的二进制,如 1→001,而不能写成 1→01或者 1→1。
3. 八进制转换为十六进制
八进制到十六进制的转换通常以二进制为中介,即先将八进制转换为二进制,然后再由二进制转换为十六进制。
范例2.5 :将八进制754231 (8) 转换为十六进制
解析:先将八进制数 754231 (8) 转换为二进制
754231 (8) →111/101/100/010/011/001 (2) →111101100010011001 (2)
再将二进制转换为十六进制
111101100010011001 (2) →0011/1101/1000/1001/1001 (2) →3/D/8/9/9 (16) →3D899 (16)
十六进制数是C语言中主要的赋值方式之一,同时也是二进制在C语言中的主要表现方式,在后续章节的C语言内存讲解及程序调试过程中,它将会得到广泛地使用。
1. 十六进制转换为十进制
十六进制向十进制的转换同样按照位权和数码相乘再依次相加的方法。例如,下面的数制转换等式:
与二进制、八进制到十进制的转换类似,十六进制数 13FB (16) 到十进制的转换计算公式为:
算式中下标(16)和(10)称做基数;16 x 称做位权;1、3、F和B称做数码。计算时幂指数可自右向左按数码位置从 0 算起,计算得十六进制数 13FB相当于十进制数 5115。
2. 十六进制转换为二进制
十六进制数向二进制数的转换可以看做是二进制到十六进制的逆运算,转换方法为将十六进制数从右到左每位数字转换为 4 位二进制数,转换方法请参看表 2-2 所示,并去掉最左边的 0 位。
范例2.6 :将十六进制数FB1A4 (16) 转换为二进制
解析:将十六进制数从右到左每位转换为 4 位二进制数
3. 十六进制转换为八进制
十六进制转换为八进制同样需要二进制做中介。
范例2.7 :将十六进制数3C6D (16) 转换为八进制数
解析:先将十六进制数 3C6D (16) 转换为二进制
再将其转换为八进制
十进制到二进制的转换分成两部分,一部分是整数部分的转换,另一部分是小数部分的转换。
1. 整数部分转换
整数十进制到二进制的转换采用除二取余再反向的方法,即将整数做除二取余运算,直到被除数为零,然后将余数反向顺序写出,就是整数部分的二进制表达。
范例2.8 :将十进制数158转换为二进制数
解析:首先对 158 进行除二取余运算
158/2=79......0
79/2=39 ......1
39/2=19 ......1
19/2=9 ......1
9/2=4 ......1
4/2=2 ......0
2/2=1 ......0
1/2=0 ......1
等号右边是每次运算所得的商,省略号后面是本次运算的余数,将所得余数自下而上按顺序从左到右写出 10011110,这就是十进制数 158 的二进制表示。
2. 小数部分转换
小数部分十进制到二进制的转换采用乘二取整再顺序写出的方法,即将小数部分与 2 相乘,记录乘积的整数部分,将小数部分再与 2 相乘,记录乘积的整数部分,这样执行下去直到小数部分为 0 或满足要求精度。将所记录的整数部分按前后顺序从左往右写出,即得二进制形式。
范例2.9 :将十进制数0.375转换为二进制数,要求精确到小数点后6位
解析:对二进制数 0.375 做乘 2 取整运算
0.375*2=0.700 ......0
0.700*2=1.400 ......1
0.400*2=0.800 ......0
0.800*2=1.600 ......1
0.600*2=1.200 ......1
0.200*2=0.400 ......0
将上述所记录整数部分顺序写出 0.010110,这就是小数 0.375 的近似二进制表达。
十进制小数到二进制的转换经常遇到无限循环的情况,这时需要指定转换的精度,例如需要精确到小数点后 8 位,计算到二进制小数点后 8 位即可停止运算。
在计算机中,数据是以二进制形式存储的,而在内存中二进制数以字节为单位进行存储。通常,C语言中会经常提到描述二进制数的两个概念bit和byte,前者是一个二进制位 0 或 1,后者是指一个字节,表示 8 个二进制位。在内存中以二进制存储的数据称为机器数,机器数的存储有几种不同的表示方式,分别叫做原码、反码和补码。
1. 机器数
机器数的表示形式为用“0”表示正数,“1”表示负数,其余位表示数值,通常把在计算机内存中正、负号数字化的数称为机器数。C语言中的基本整型数据在计算机中通常用 32位(即 4 个字节)来存储,后续章节中将会讲解有关 32 位机的概念。
2. 原码
原码是计算机中数据存储方式之一,其表示形式为数值用绝对值表示,在数值的最高位用“0”和“1”分别表示数值的正和负。
范例2.10 :写出+35和-35的原码表示形式(32位表示)
解析:首先确定数据的符号作为最高位,然后将数值转换为二进制数,以 32 位表示
[+35] 原码=00000000000000000000000000100011
[-35] 原码=10000000000000000000000000100011
注意:0 的原码有两种表示方式,即正 0 和负 0,分别为
[+0] 原码=00000000000000000000000000000000
[-0 ]原码=10000000000000000000000000000000
3. 反码
反码在计算机中的表示方式为正数的反码与原码相同,负数的反码是其原码数值部分按各位取反,符号位不变。
范例2.11 :写出+35和-35的反码表示形式(32位表示)
解析:首先分别写出两个数的原码,以 32 位表示
[+35]原码=00000000000000000000000000100011
[-35]原码=10000000000000000000000000100011
再将负数 35 的原码取反,得+35 和-35 的反码
[+35]反码=00000000000000000000000000100011
[-35]反码=11111111111111111111111111011100
4. 补码
计算机补码的表示形式为正数的补码与原码、反码相同,负数的补码是其反码加 1,符号位不变。
范例2.12 :写出+35和-35的补码表示形式(32位表示)
解析:首先分别写出两个数的原码,以 32 位表示
[+35]原码=00000000000000000000000000100011
[-35]原码=10000000000000000000000000100011
再将负数 35 的反码加 1,得+35 和-35 的补码
[+35]补码=00000000000000000000000000100011
[-35]补码=11111111111111111111111111011101
5. 0的反码和补码
在反码和补码表示中,0 是一个比较特殊的数字,由于 0 可表示为正 0 和负 0,因此 0的原码和反码分别有两种表示形式,如下表示
[+0]原码=00000000000000000000000000000000
[-0]原码=10000000000000000000000000000000
[+0]反码=00000000000000000000000000000000
[-0]反码=11111111111111111111111111111111
而对于+0 和-0 的补码,有
[+0]补码=00000000000000000000000000000000
[-0]补码=00000000000000000000000000000000
可见 0 的补码表示是唯一的。