下载掌阅APP，畅读海量书库
立即打开
有限差分法（Finite Difference Method，FDM）是最早采用的计算机数值模拟方法之一，至今仍被人们广泛应用。例如当前被NASA广泛使用的SINDA/FLUINT等软件，就是采用集总参数加有限差分法来实现的。
有限差分法的基本思想是把连续的求解区域用有限个离散点构成的网络代替，这些离散点被称为网格节点。然后以Taylor级数展开等方法，把数理方程中的微分项用差商来近似，积分用数值积分或求和来近似。经过这些近似，就可以用代数方程组来近似地代替所需求解的偏微分方程（组）和定解条件。最后利用插值方法，通过离散的网格节点上的结果得到整个区域上的解。
有限差分法的特点是数学概念直观，表达简单，容易理解和使用。举个简单的例子，如图1.2所示的一根直杆，左端固定温度为 T 0 ，右端固定温度为 T N 。
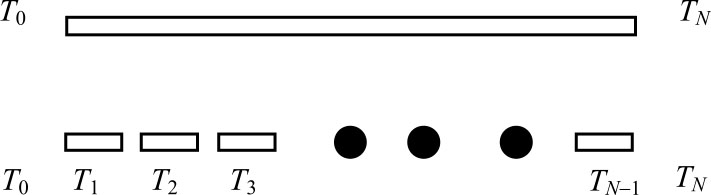
图1.2 直杆传热，上图：直杆示意图，下图：离散示意图
前文已经讲述过热传导方程了，所以这里只简要介绍一下它的差分形式。首先，将这根杆离散成 N 段，每段具有对应的材料属性，包括热容、传热系数等，用 k 来表示。
然后将偏微分方程形式进行近似，得到如方程式（1.34）的显式差商形式
其中 i 表示每段的序号，加上两端是已知的条件，以及初始值，就可以得到定解。从 i =1开始，一个个式子求解下去，直到 i = N 。最终就可以得到我们想要的结果。
显而易见，离散时采用的数量、离散方法，求解时采用的时间步长等对于解的影响是很剧烈的。为了提高求解精度和速度，还可以采用隐式或其他各种更加先进的差分处理方法。
总地来看，有限差分法比较直观，计算速度相对比较快，易于编程，易于加入并行算法。缺点在于不易处理复杂的求解域，对网格和解的连续性要求比较严格。