




代数、几何、解析几何、矩阵和概率这几个看似各自为政的数学模块,实际上有紧密的内在联系。本章和下一章从矩阵运算入手,用若干例子来讨论它们之间的关联。
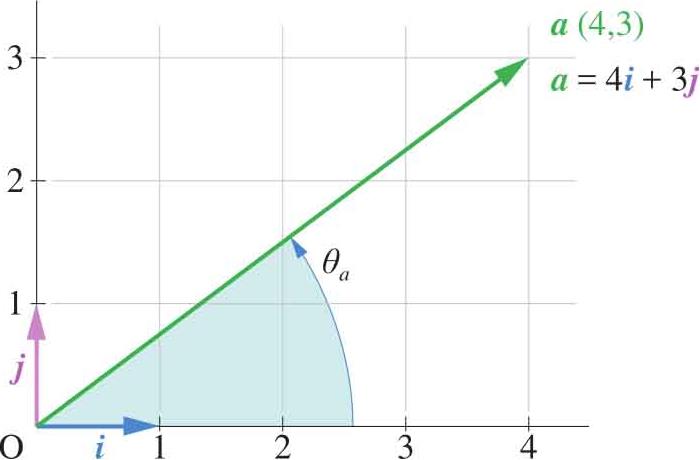
图1.1 平面中的向量
丛书第一本第5章探讨了平面和空间概念。本章聊一聊空间中的向量。如图1.1所示是平面向量的表达方法:

也可以写成:

向量有两个很重要的元素:长度和角度。向量的长度,叫作 欧几里得范数 (Euclidean norm of the vector)。对行向量 a =[ a 1 , a 2 ],它的范数为:

式(1.3)所示向量的角度可以求解为:

另外一个重要的概念是, a 方向上的单位向量 (unit vector in the direction of a):

如图1.2所示是平面向量的加法、倍数和减法的运算规则,此处不再赘述。
数量积 (scalar product),也叫 内积 (inner product),是向量乘积的一种。对于二维空间, a =[ a 1 , a 2 ]和 b =[ b 1 , b 2 ]两个行向量的内积可以表达为:

上式为行向量内积计算;这个运算规则也适用于列向量。
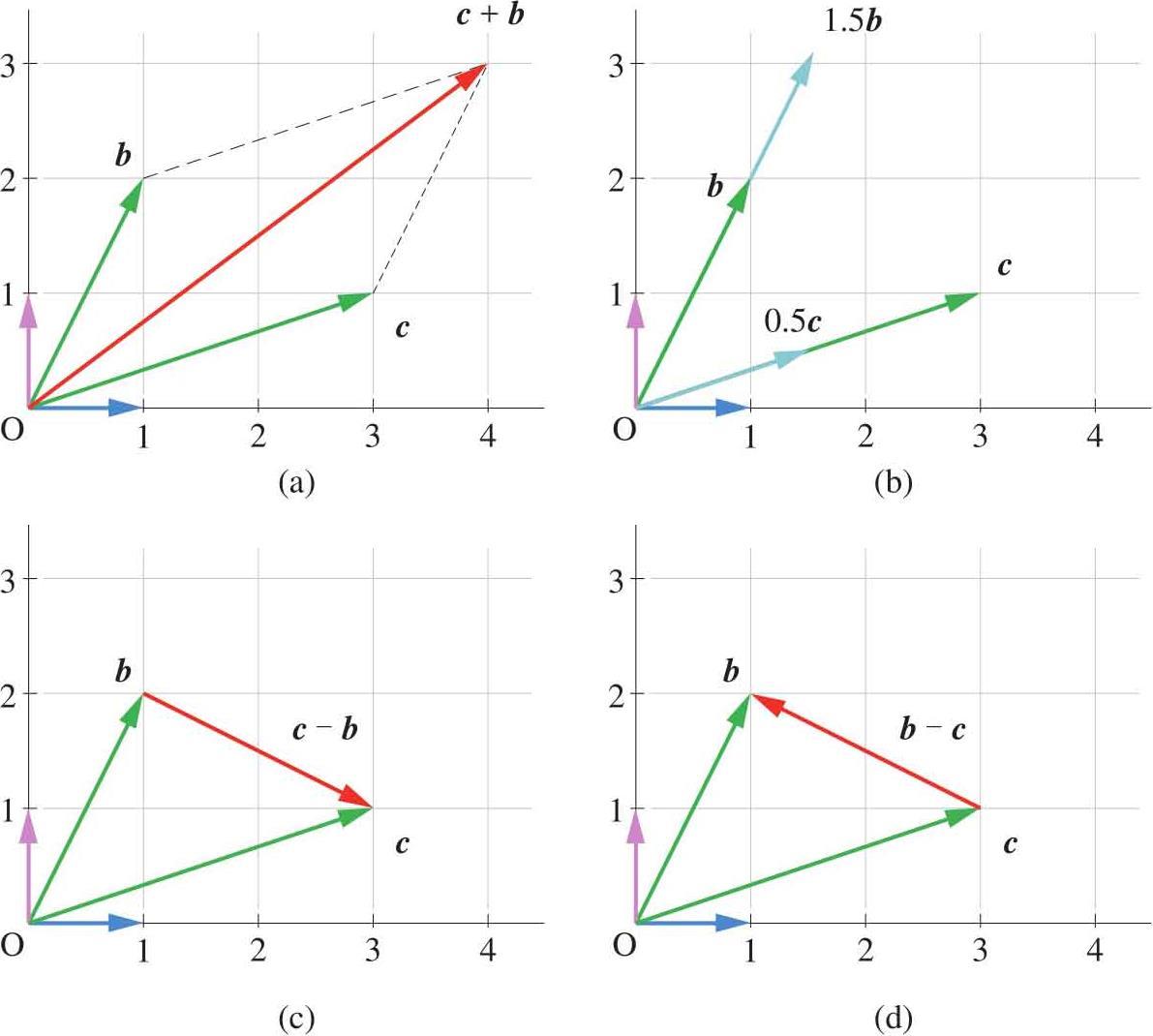
图1.2 平面中的向量加法和减法
有两个多维行向量, a =[ a 1 , a 2 ,…, a n ]和 b =[ b 1 , b 2 , …, b n ],这两个多维行向量的内积计算式为:
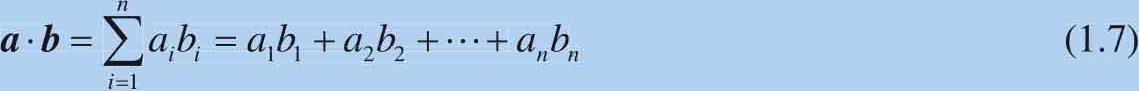
式(1.7)所示内积可以用矩阵的乘积来表达:
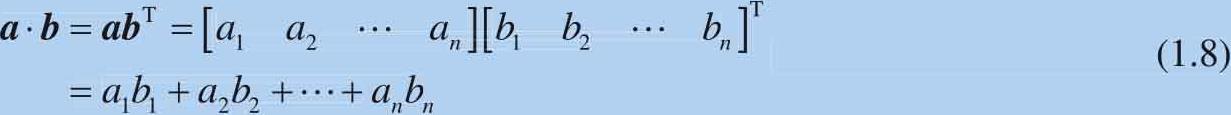
请读者自行推导多维列向量内积计算式。内积和向量夹角 θ (如图1.3所示)有直接联系:

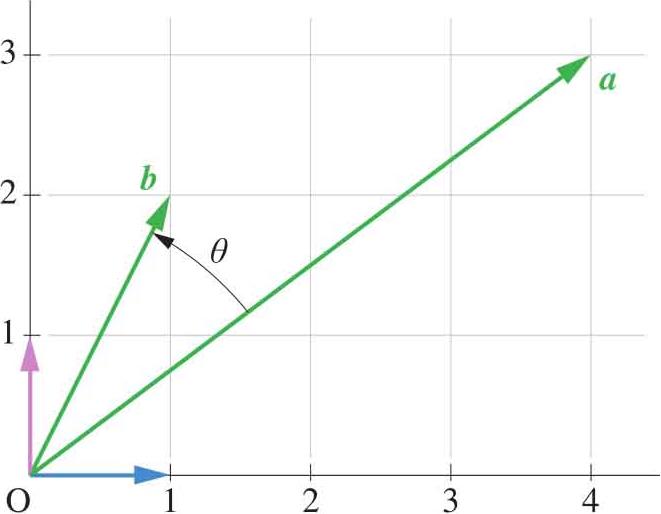
图1.3 直角坐标系,向量的夹角
行向量 a 、 b 的夹角 θ 可以通过式(1.10)计算得到:

行向量 a 的范数也可以通过内积来求得:

行向量 a 和自身的夹角为 θ =0°。对于二维空间,cos θ 可以通过式(1.12)求得:
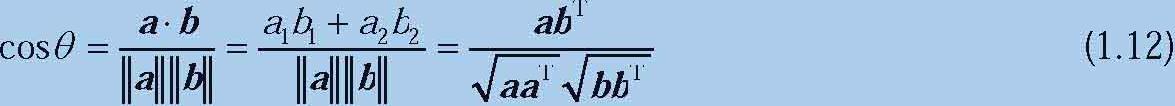
下面,将向量 a 、 b 放在极坐标中解释向量夹角。 a =[ a 1 , a 2 ]和 b =[ b 1 , b 2 ]在极坐标中各自的角度为 θ a 和 θ b ,如图1.4所示。两个向量和各自坐标的关系:

cos θ 可以由 θ a 和 θ b 正余弦构造:
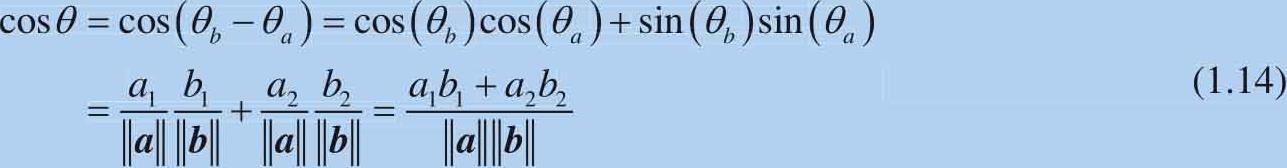
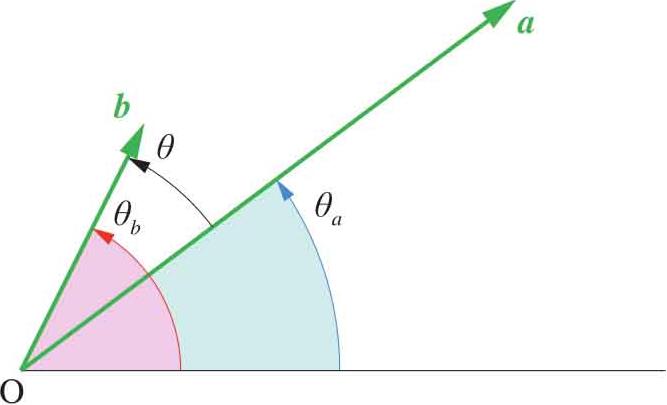
图1.4 极坐标中解释向量夹角
另一种在MATLAB编程中常用的矩阵乘法叫作 元素乘积 (element-wise multiplication),也称为 哈达玛积 (Hadamard product),或 元素相乘 或 逐项积 ,即两个形状相同的矩阵,对应元素相乘得到同样形状的矩阵。如图1.5所示是元素乘积的运算。还有一种向量的乘积叫作 叉乘 (cross product, vector product),也叫作 向量积 ,丛书第四本中将会介绍叉乘运算。
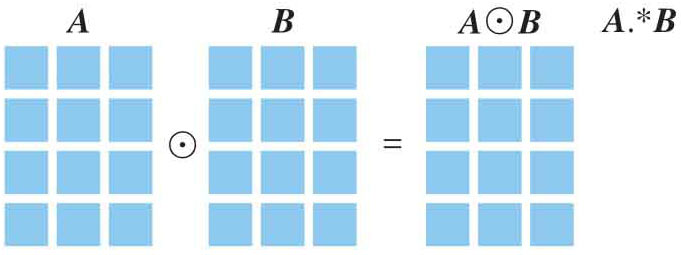
图1.5 矩阵的元素乘积
有了以上向量的基础知识,接着看一看向量的 投影 (projection)。向量投影主要有两种, 标量投影 (scalar projection)和 向量投影 (vector projection)。下面我们介绍的是标量投影,也就是投影结果是标量形式。向量 a 可以在 x 和 y 轴上投影,也可以在任何其他坐标系内投影,这些坐标系可以是 正交系 (orthogonal coordinates),也可以是 非正交系 (nonorthogonal coordinates)。如图1.6所示是平面中的一个向量 a 在不同的正交坐标系内投影到坐标轴的情况。
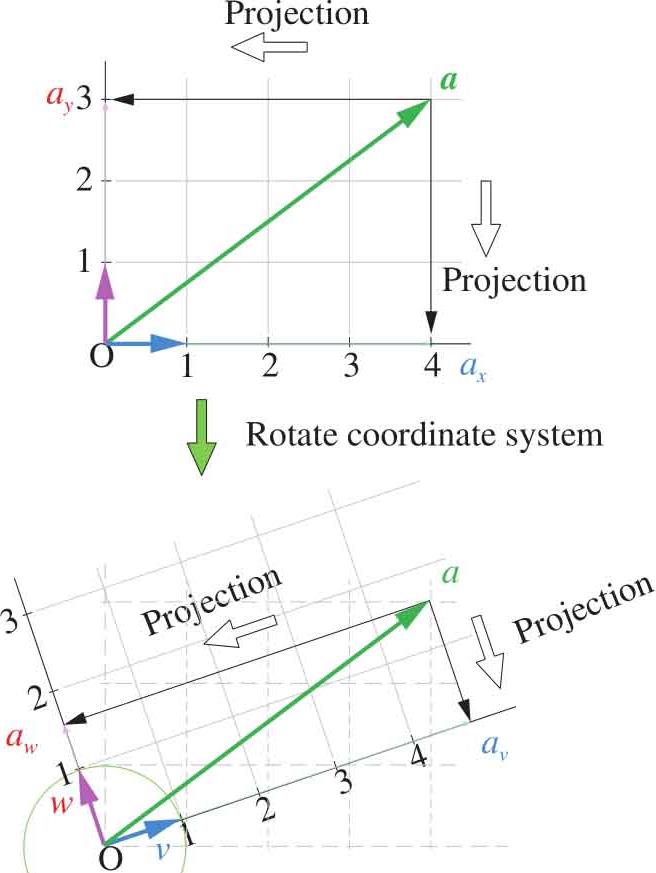
图1.6 平面中向量在不同坐标系的投影
如图1.7所示,若向量 a 在单位向量 v 1 方向的投影为 c v 1 ,那么向量 a 和向量 c v 1 的差得到的向量 c v 1 - a 与向量 v 1 相互垂直,即有:

如果 a 和 v 1 都是列向量,式(1.15)可以写作:

a T 是 a 的转置,结果为行向量。比如 a =[4,3] T 在 v 1 =[1,0] T 方向上投影可以得到:

a =[4,3] T 在 v 2 =[0,1] T 方向上投影可以得到:

如果有如式(1.19)所示正交坐标系:

向量 v 1 和 v 2 长度为1,都是单位向量。另外,如式(1.20)成立,说明这两个单位向量正交:

下面把 a T =[4,3]投影到这个正交系中:
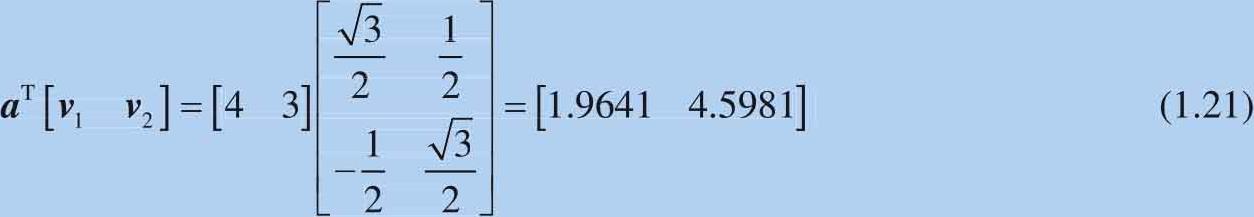
如果把 v 1 和 v 2 交换,可以得到:
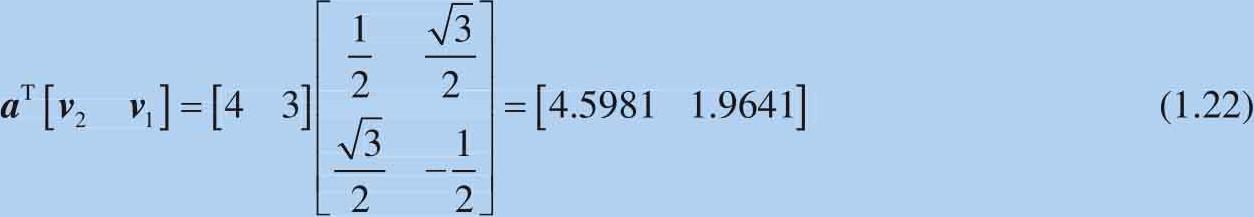
可见结果的坐标值也发生了交换。注意,坐标系的旋转方向和坐标系内向量的旋转方向是相对的,如图1.8所示。如果构建式(1.23)所示矩阵:

其中, V 这个矩阵的转置和 V 本身乘积是一个单位矩阵:

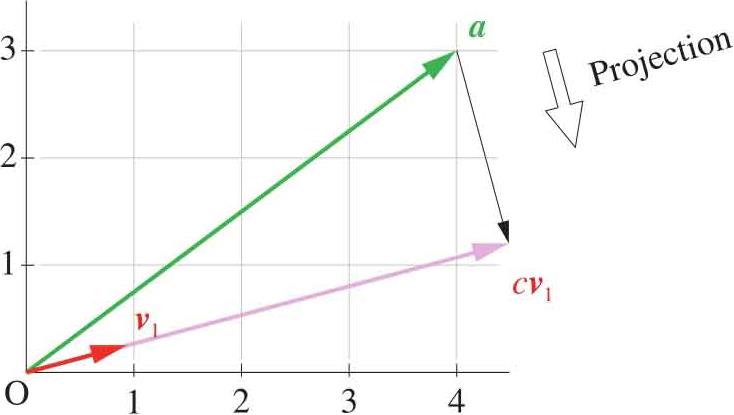
图1.7 向量 a 在单位向量 v 1 方向的投影
本章后续内容还会更加深入探讨对称、旋转等变换。
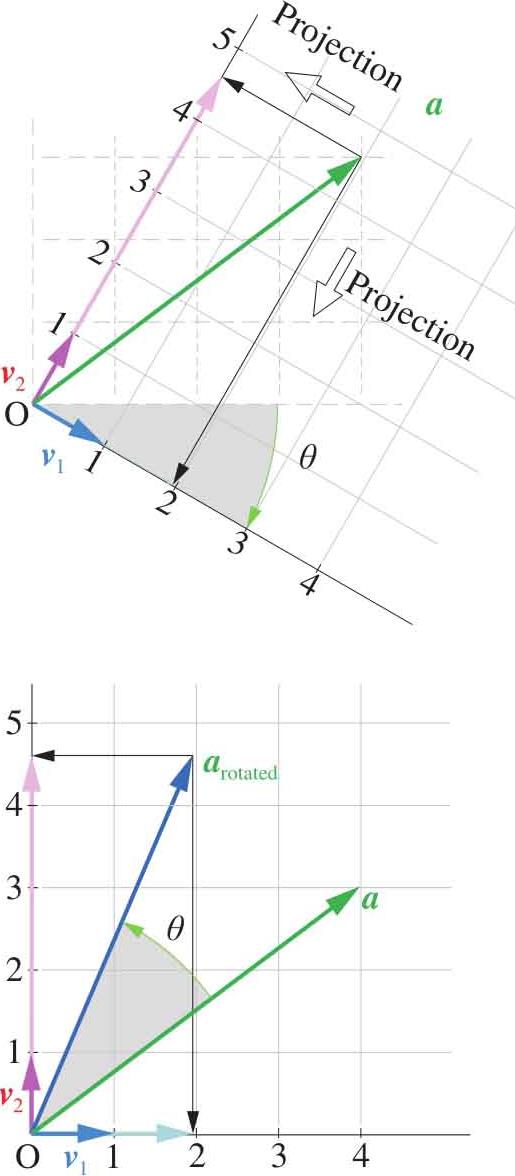
图1.8 坐标系的旋转和向量的旋转的方向关系
接下来再介绍一下 特征值 (eigenvalue)和 特征向量 (eigenvector)。特征向量代表方向,通常是列向量;特征值是在这个方向上的比例,特征值是标量。给定方阵 A ,它和特征向量、特征值满足式(1.25)的关系:

某个二维矩阵 A ,有两个特征值和特征向量:

特征向量 Av 1 、 Av 2 可以构成一个矩阵 V ,用两个特征值构造一个对角阵,式(1.26)可以写成:

式(1.27)叫作 矩阵的特征分解 (eigen-decomposition of a matrix)。在MATLAB中,特征分解的MATLAB函数是[ V , Λ ]=eig( A )。特征值、特征向量和特征分解这三个概念在本书特别重要,请读者多加留意。丛书第四本会专门讨论向量和矩阵投影和特征值分解、Cholesky分解、SVD分解、PCA分析之间的紧密联系。
行列式 (det erminant),是将一个方阵 A 根据一定的规则映射到一个标量,记作det( A )或| A |。二阶矩阵的行列式的计算规则为:

MATLAB用于计算行列式值的命令为det(),如下代码, A 的行列式结果为10。
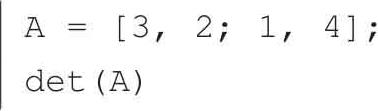
如图1.9所示是二阶矩阵行列式的几何意义。图中蓝色平行四边形的面积就是 A 的行列式值,它可以通过整个矩形面积减去四个三角形面积得到:
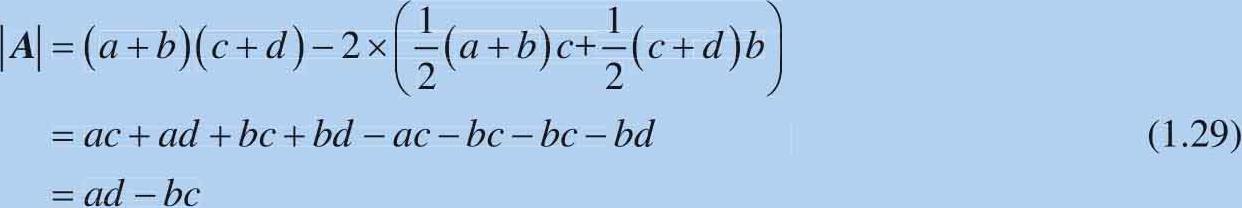
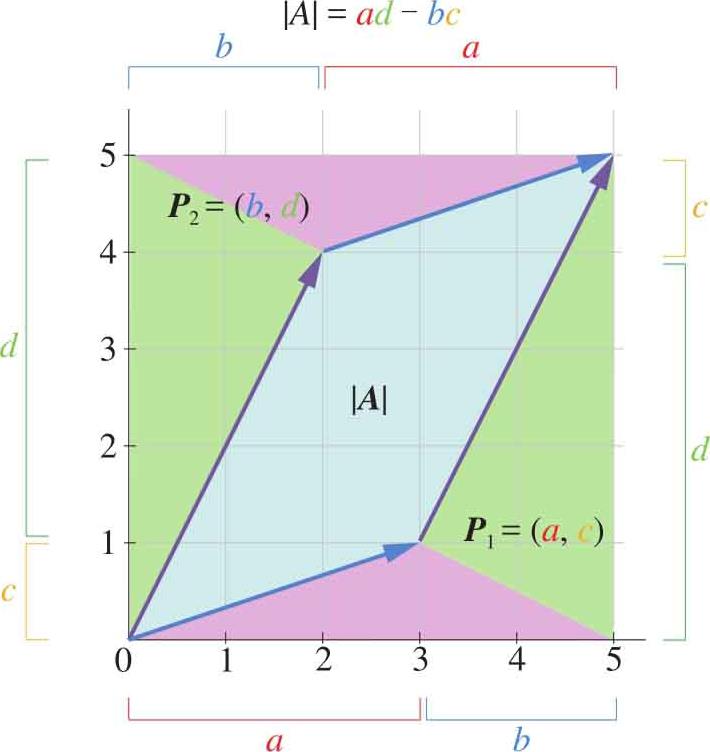
图1.9 二阶矩阵的行列式的几何意义
三阶矩阵的行列式计算规则为:

正如二阶矩阵行列式能够造出平面面积,三阶矩阵的行列式在三维空间可以构造得到体积量值。丛书第四本介绍向量叉乘运算时,还要利用三阶矩阵行列式计算。