平面内某点 m 到样本集合 X 中心的 欧拉距离 (Euclidean distance)可以通过式(2.66)计算得到:

式中: m 为空间某一点,由行向量表示; μ X 为空间样本点集合 X 中心位置(均值位置)。
如图2.19所示是一组空间样本点集合
X
和四个散点(
A
、
B
、
C
和
D
)。可以发现
A
和
B
到数据中心
μ
X
的欧氏距离为
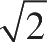 ;
C
和
D
到数据中心
μ
X
的欧氏距离为1。就
A
和
B
点来说,发现欧氏距离不足以描述两点和数据
X
的关系。虽然
A
和
B
距离数据中心(均值点)距离相同,但是显然从数据分布角度来说,
B
距离数据
X
更近一些,
A
远离数据中心。这是因为
X
在不同方向上分布密度不同。比较
C
和
D
,同样地,从数据分布角度来看,
D
距离
X
更近。因此,需要定义一种新的度量。
;
C
和
D
到数据中心
μ
X
的欧氏距离为1。就
A
和
B
点来说,发现欧氏距离不足以描述两点和数据
X
的关系。虽然
A
和
B
距离数据中心(均值点)距离相同,但是显然从数据分布角度来说,
B
距离数据
X
更近一些,
A
远离数据中心。这是因为
X
在不同方向上分布密度不同。比较
C
和
D
,同样地,从数据分布角度来看,
D
距离
X
更近。因此,需要定义一种新的度量。
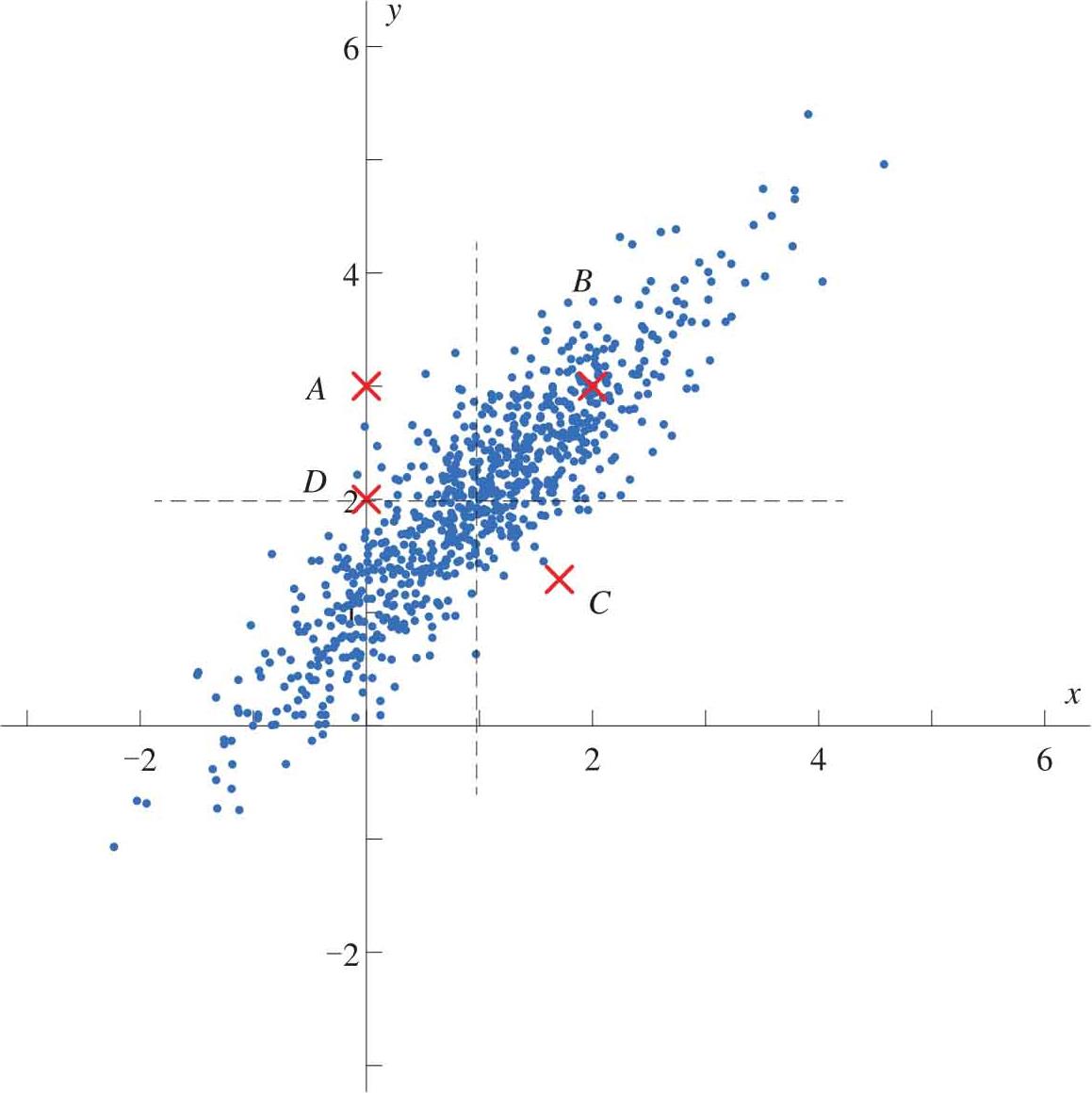
图2.19 x - y 平面的 X 数据和四个散点( A 、 B 、 C 和 D )
对于一维数据, z 值、 标准分数 (z-score, standard score)回答了“某个点距离平均数多少个标准差”这样一个问题。而标准差的长度表达的就是分布的密度,某个维度的标准差越大,这个维度上数据密度越小。多维标准正态随机数据的 Z 值可以通过空间转换,表达在正交系中:

丛书第四本将会从线性变换和投影角度再次探讨式(2.67)。有了以上讨论,可以介绍研究多维统计数据关系常用的一种度量值, 马氏距离 (Mahalanobis distance, Mahal distance),也叫 马哈距离 。马氏距离就是用正交化、归一化的坐标系来度量某个数据点 m 和数据整体 X 的距离。马氏距离的定义为:

Σ 为数据 X 的方差-协方差矩阵。马氏距离是众多 统计距离 (statistical distances)的一种。 Σ 可以表达为:

对应的 Σ -1 为:
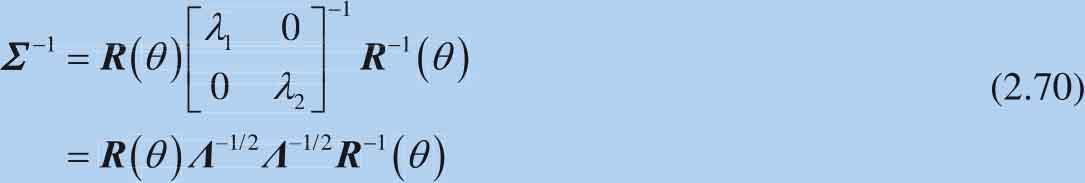
将式(2.70)代入马氏距离计算式:
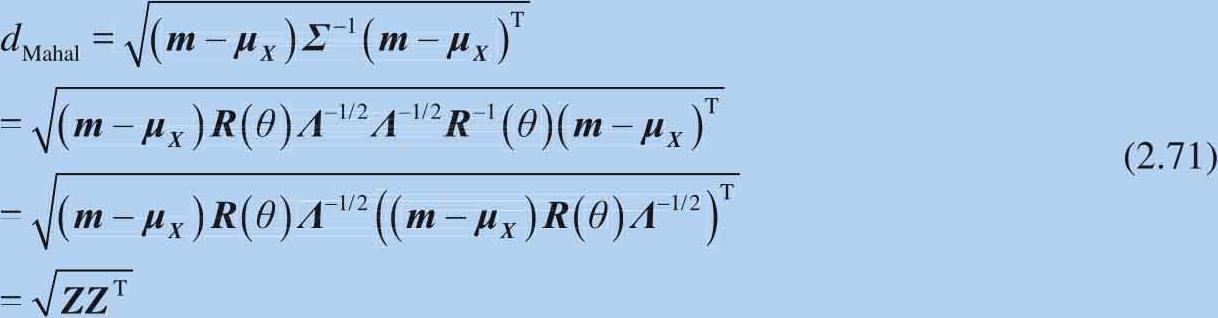
式(2.71)就是经过矩阵转化得到的以标准差为单位坐标系的距离。来看一种特殊情况,如果线性相关性系数为0的 X 数据方差-协方差矩阵为:

方差-协方差矩阵的逆 (inverse of the variance-covariance matrix)为:

通过之前的讨论,马氏距离可以通过下式求得:
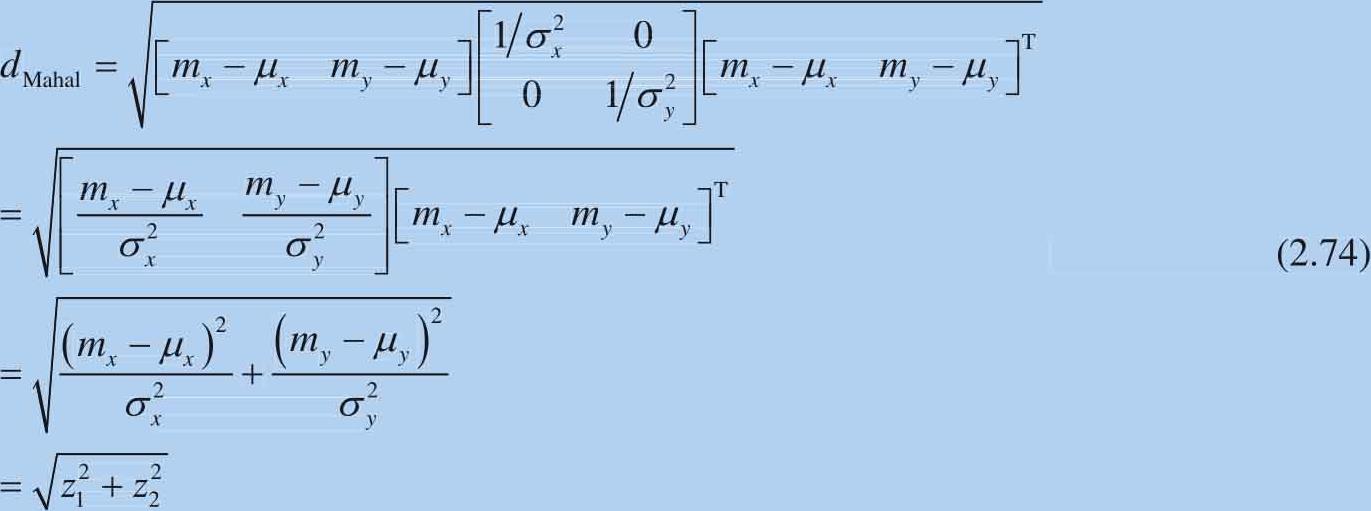
如图2.20所示是图2.19数据 X 和四个点 A 、 B 、 C 和 D 在方差正交的网格中的位置。 A 距离数据中心的“网格数”大于4; B 距离数据中心的“网格数”约为1,这明显说明相比 B , A 距离数据 X 更远。如图2.21所示是另外一种可视化。上一节,知道椭圆可以用来表达二维置信区间。图2.21中给出的同心椭圆表达的是等均方差。 A 的马氏距离为4.3798,它在第四和第五个椭圆之间; B 的马氏距离为1.0588,它几乎落在第一个椭圆之上; C 的马氏距离为3.1386,它在第三个椭圆之外; D 的马氏距离为2.2159,它在第二个椭圆之外。
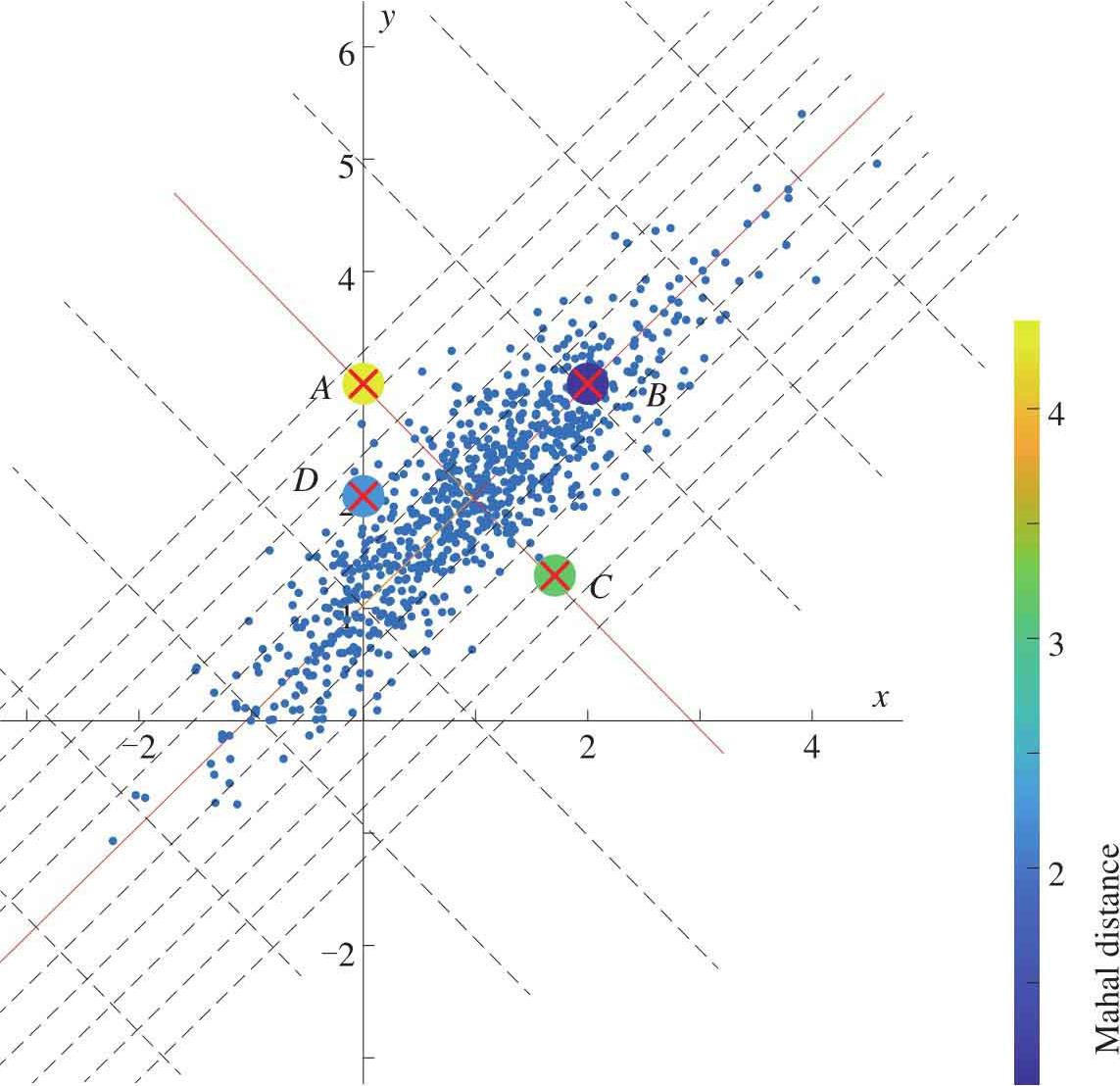
图2.20 方差正交网格
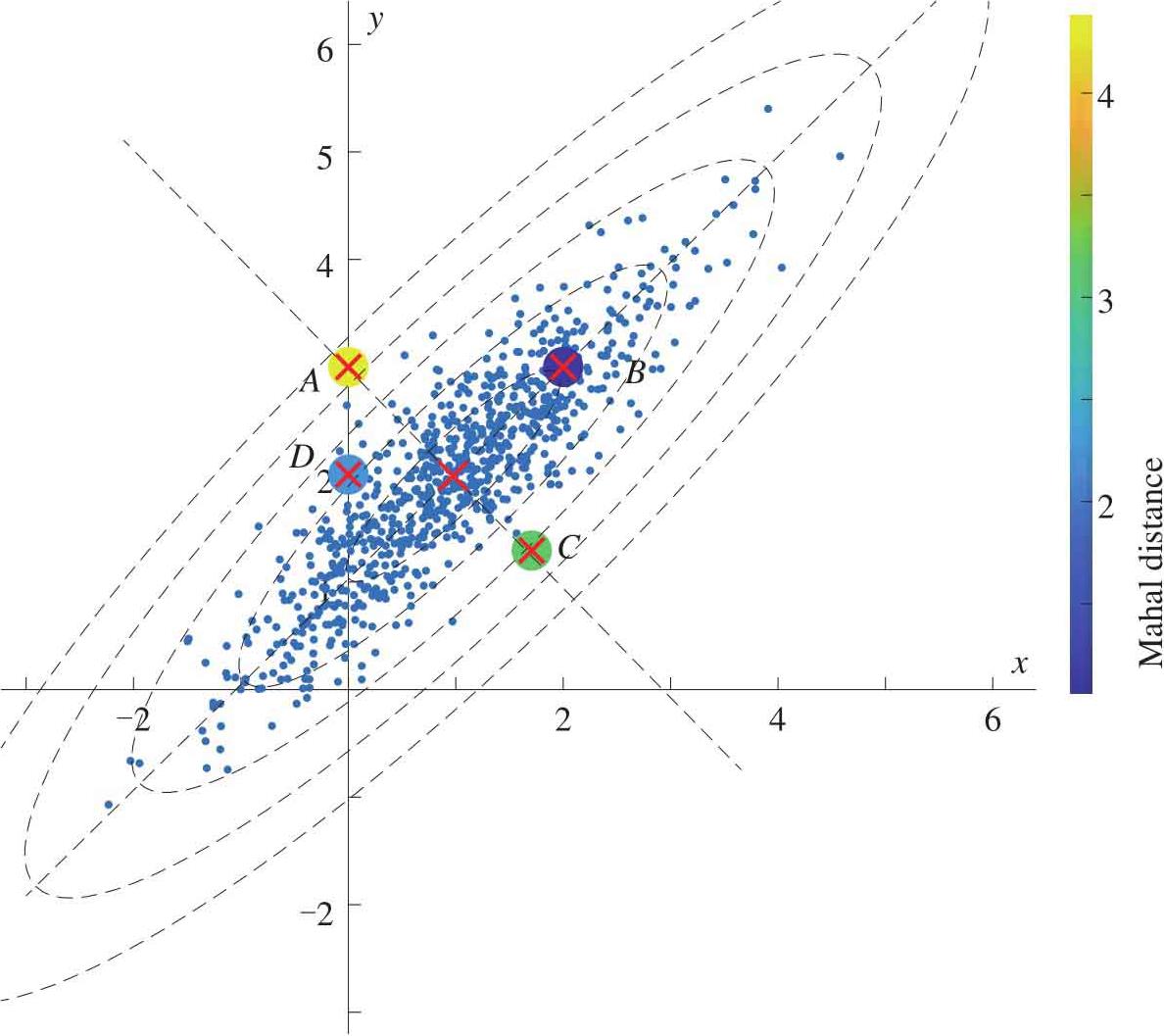
图2.21 正交方差系内的等均方差椭圆
图2.21数据 X 和 A 、 B 、 C 和 D 四点,经过转换后可以得到去相关中心化数据,如图2.22所示。此时,图2.21的椭圆变成同心正圆;图2.22中的欧式距离就是图2.21的马氏距离。
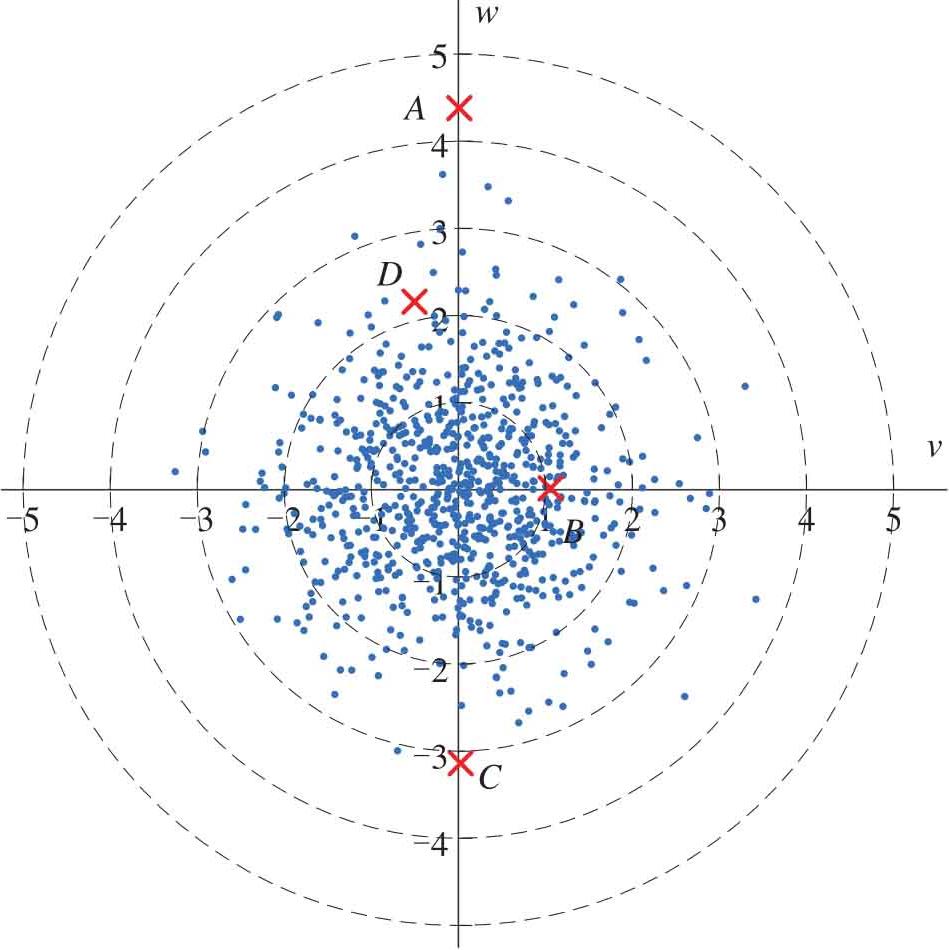
图2.22 经过坐标转换的数据和等方差同心正圆
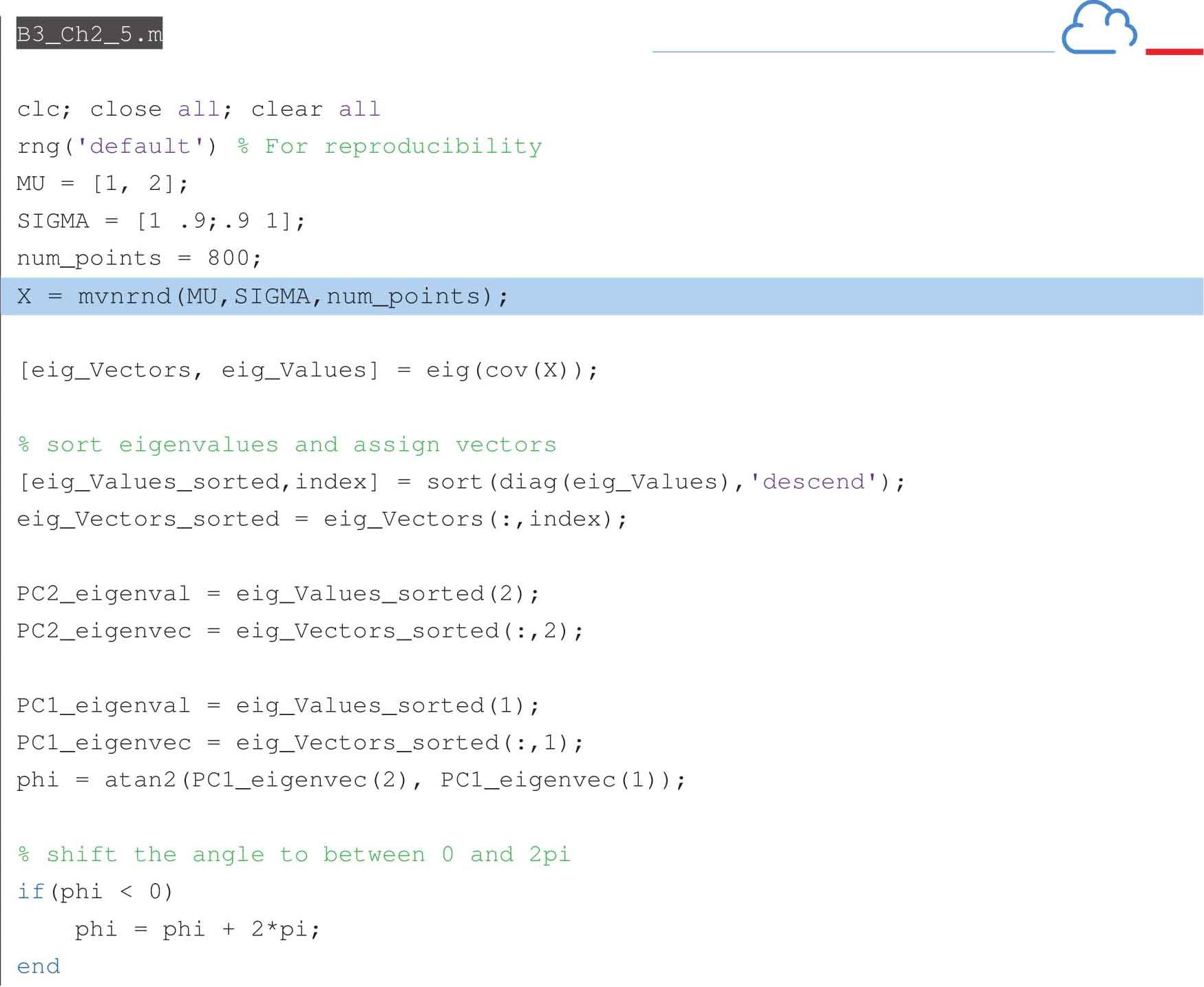
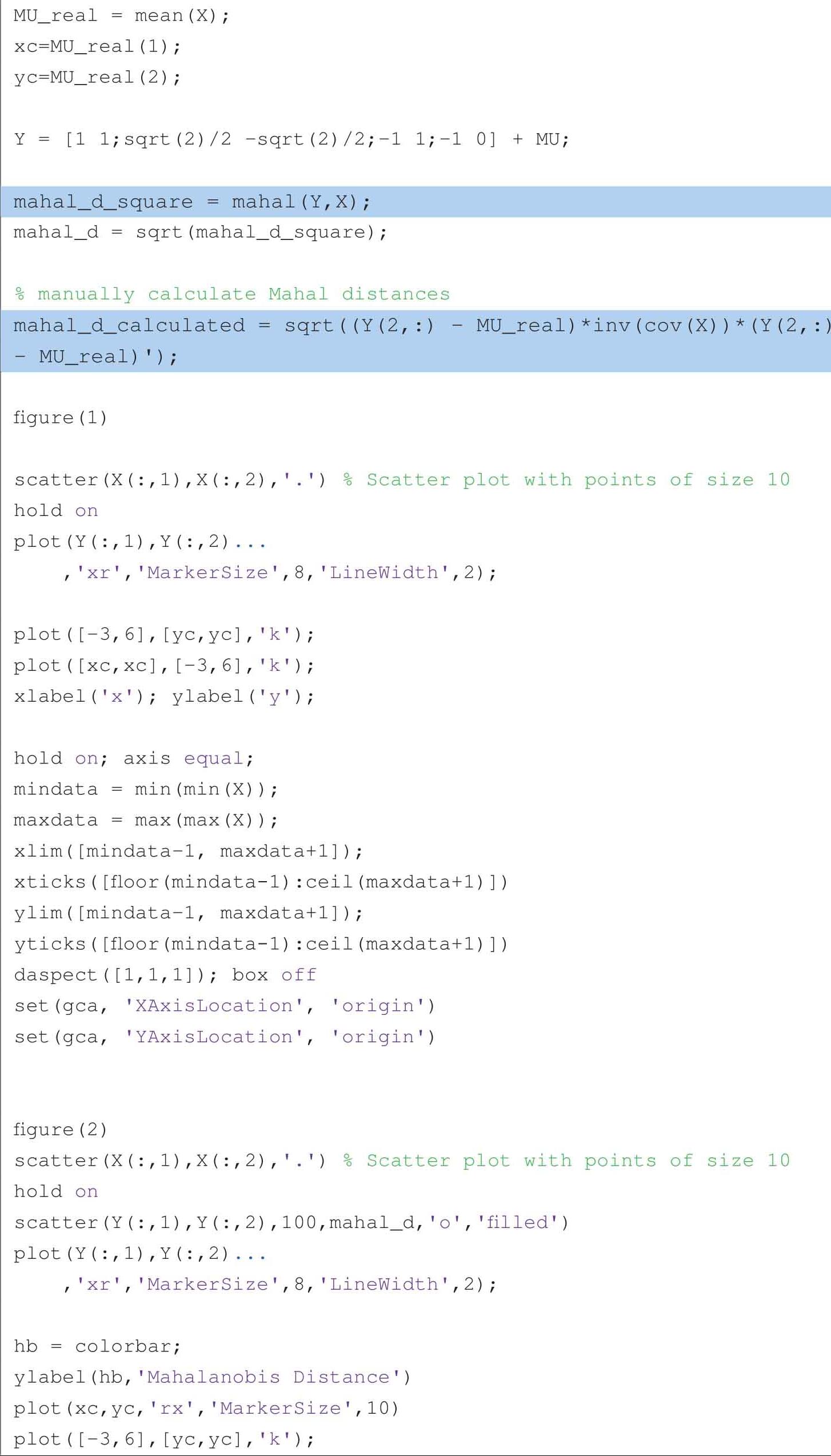
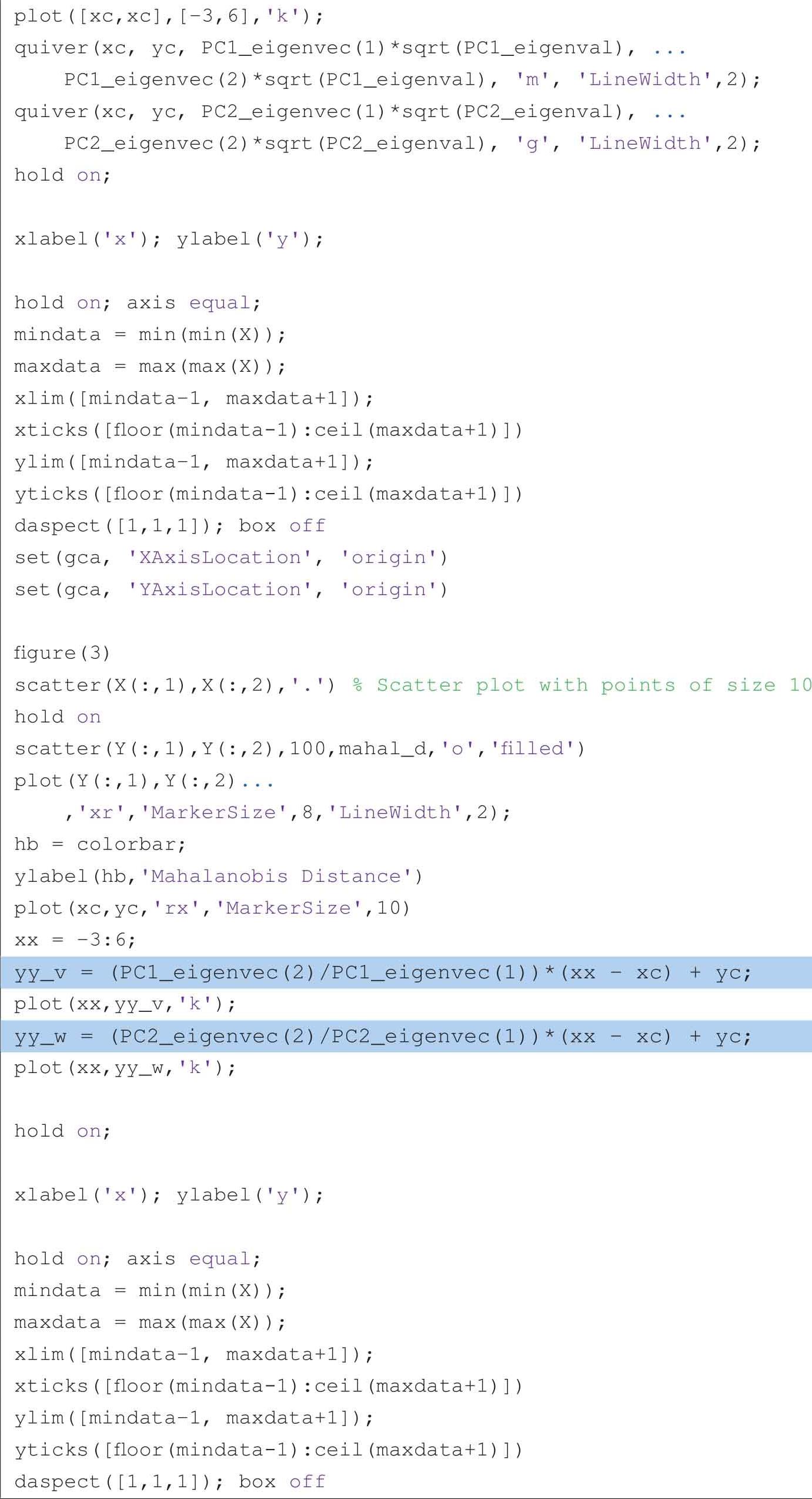
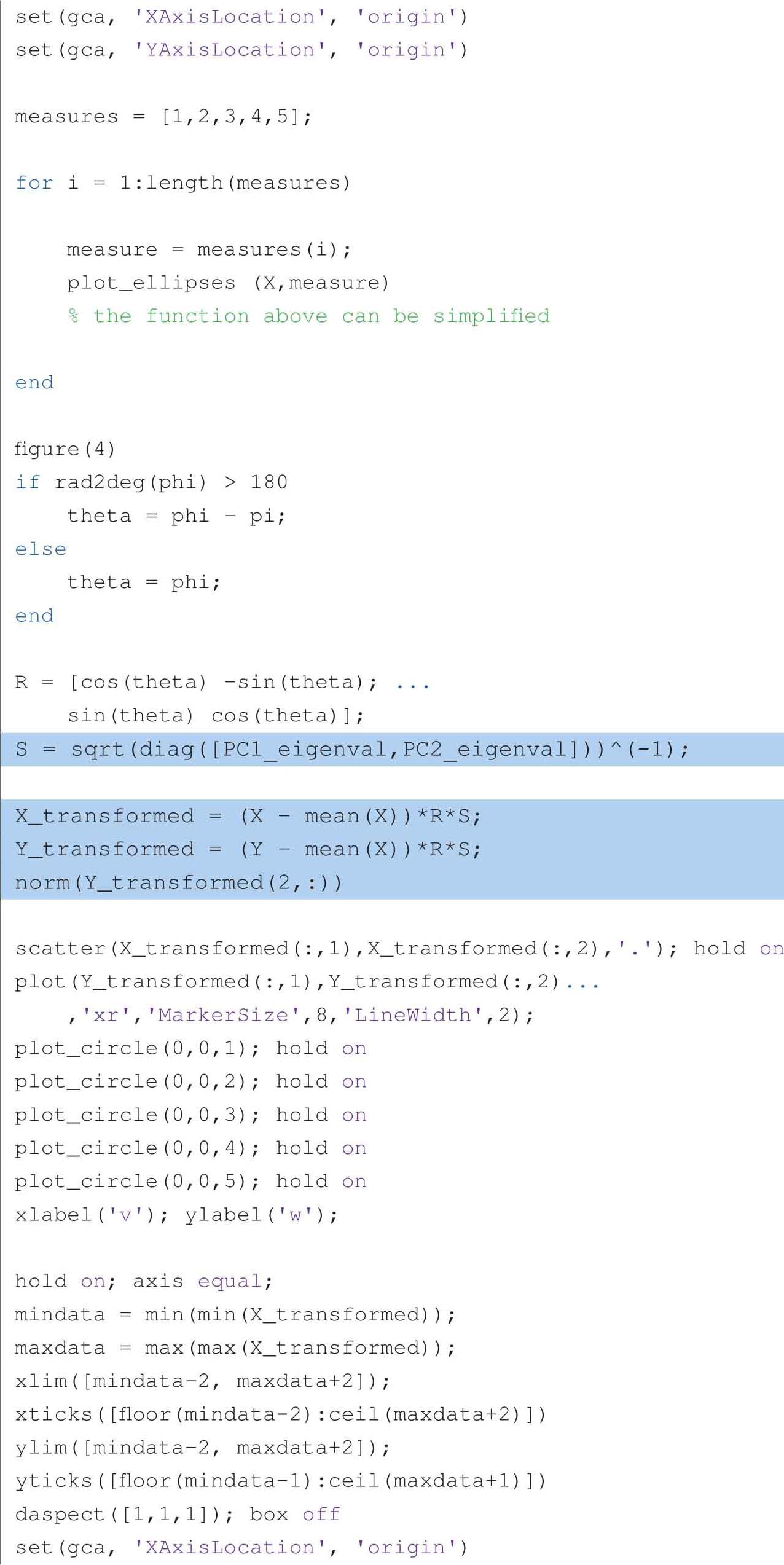
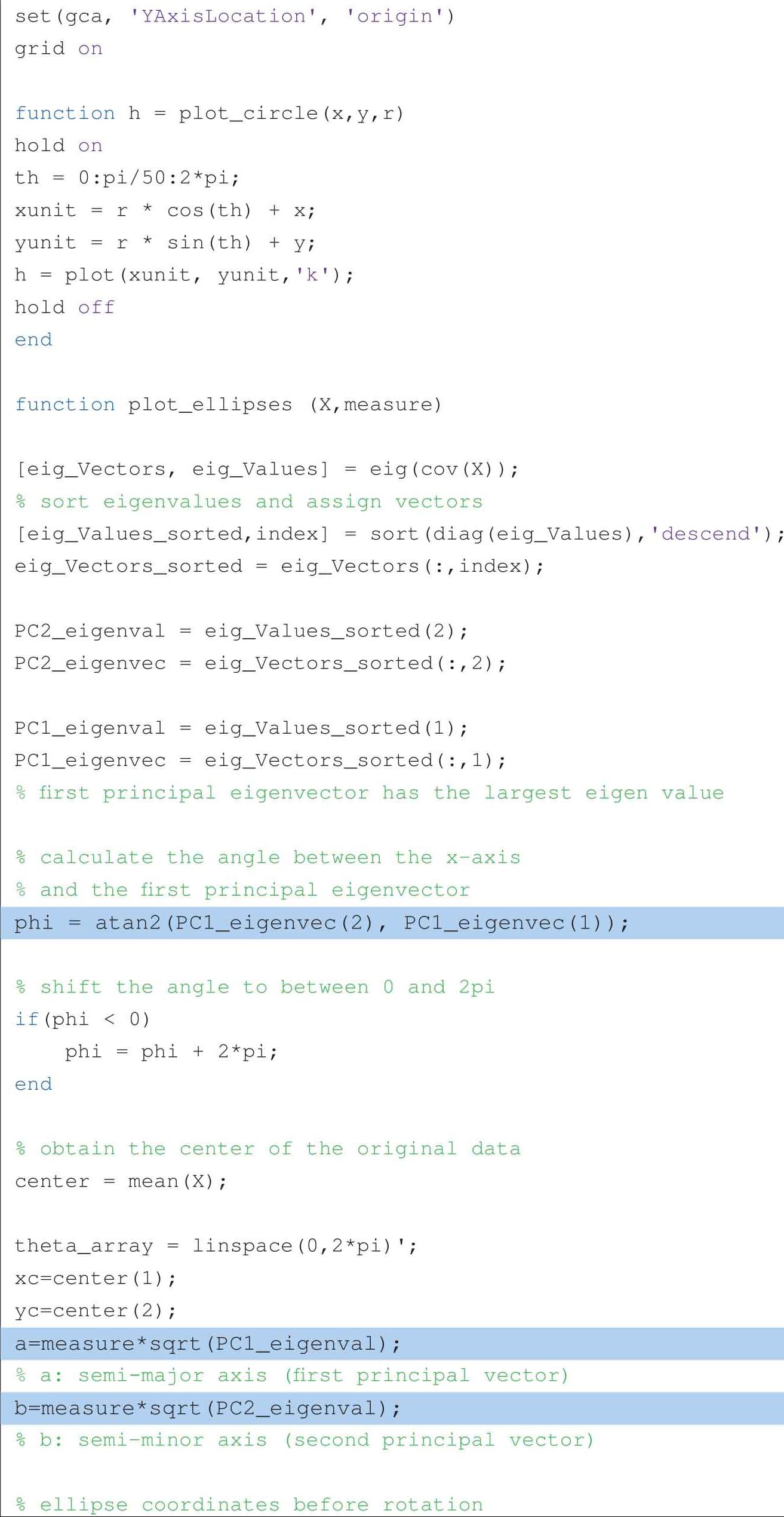
以下代码可以获得图2.19到图2.22: